微波视觉三维SAR关键技术及实验系统初步进展

仇晓兰 焦泽坤 杨振礼 程 遥 蔺 蓓 罗一通 王 卫 董勇伟 周良将 丁赤飚*

①(微波成像技术国家级重点实验室 北京 100190)

②(苏州市空天大数据智能应用技术重点实验室 苏州 215123)

③(苏州空天信息研究院 苏州 215123)

④(中国科学院空天信息创新研究院 北京 100190)

⑤(中科宇达(北京)科技有限公司 北京 100190)

1 引言

合成孔径雷达(Synthetic Aperture Radar,SAR)三维成像能够解决三维目标及场景投影至二维成像平面而造成的叠掩问题，在陡峭地形测绘、城区测绘，以及目标探测和识别等方面有着重要的应用潜力，是SAR技术发展的重要方向之一。当前提出的SAR三维成像体制主要包括层析SAR和阵列干涉SAR[1]。其中，层析SAR对SAR系统本身没有特殊要求，但为了保证数据的相干性，对SAR轨道或飞行航迹的控制有严格要求，存在数据获取时间周期长、难度大的问题；阵列干涉SAR通常指具有3个或3个以上天线阵元，一次飞行就可获得3个或3个以上空间多角度相干观测的SAR系统，其能够排除时间去相干的影响，一次飞行就可实现三维成像[2]，因此成为SAR三维成像的一种重要体制，受到了各国的重视。

德国于2005年开始研制无人机载阵列三维SAR系统ARTINO (Airborne Radar for Three-dimensionnal Imaging and Nadir Observation)[3]，其利用线阵构成的实孔径以及由载机航行构成的合成孔径实现二维面阵采样。为了减少雷达阵元的个数，采用两边发射中间接收的稀疏阵列配置；同时使用能够达到低能耗以及小尺寸的调频连续波(FMWC)Ka波段雷达；使用惯性导航系统以及差分GPS传感器记录航行轨迹，使用CCD和激光单元精确记录挂载于机翼上的每个阵元的抖动误差。ARTINO整套系统安装于无人机上，该无人载机翼展4 m、重量25 kg，飞行速度10～15 m/s，实验飞行高度200 m左右。其于2010年首飞获得定标点成像结果[4,5]，试验场地的目标为3个相距10 m的角反射器，但至今没有进一步的成像试验结果报道。法国宇航局(ONERA)也开展了无人机载3D SAR系统(DRIVE系统)的研制，该系统工作于Ka波段，中心频率为35 GHz，发射信号为调频连续波，带宽800 MHz。试验载机是翼展23 m重约600 kg的滑翔机，飞行速度约50 m/s，最高飞行高度9145 m。2007年法国宇航局首次公布了其在2006年10月获取的工作于下视模式的高度方向成像结果，但目前尚未报道进一步的三维成像结果。2005年中国科学院电子学研究所开始研制机载阵列三维SAR系统，采用长2 m重150 kg的刚性大天线阵来保证基线的稳定性，于2015年获得了国际首幅三维场景成像结果[2,6]。上述现状表明，为实现三维成像，当前阵列干涉三维SAR系统的复杂度很高、研制难度很大，系统小型化及其应用推广均具有较大的难度。也即三维成像对于目前的SAR系统而言是一个“豪华选项”，需要付出很大的成本。

为改变这一现状，将SAR三维成像从“豪华选项”变为“普通选项”，由中国科学院空天信息创新研究院牵头，在国家自然科学基金重大项目支持下，正在开展“合成孔径雷达微波视觉三维成像理论与应用基础研究”，以期将三维成像对多角度观测数量的要求降低至小于等于5，从而降低系统复杂度或数据获取周期，实现高效能三维成像，促进SAR三维成像技术的应用推广[1]。在该项目支持下，中科院空天院联合中科宇达(北京)科技有限公司，设计研制了一套小型无人机载阵列干涉SAR系统，称为微波视觉三维SAR (Microwave Vision three-dimensional SAR,MV3DSAR)实验系统，用于进行数据获取和技术验证，并用于SAR微波视觉三维成像数据集的构建[7]，为该领域的研究提供必要的基础平台。目前该系统的单极化版本已经研制完成，并于2021年12月初在天津临港地区开展了首次集成校飞实验，初步验证了系统的基本性能和三维成像能力。本文介绍了该系统的基本构成、主要性能以及系统和数据处理的关键技术，给出了首次校飞实验的方案和实施情况，以及初步的数据处理结果，并指出了后续研究方向。

本文后续内容安排如下：第2节介绍了MV3DSAR基本情况和系统关键技术；第3节叙述了MV3DSAR系统校飞实验的方案及实施情况；第4节给出了数据处理流程和二维成像、系统参数标定、三维成像等关键步骤的具体方法，并给出了初步的数据处理结果；第5节总结全文并指出后续研究方向。

2 MV3DSAR系统及关键技术

为了便于开展飞行实验，降低实验成本，同时具有较高的可重构能力，支撑SAR微波视觉三维成像方法的研究和验证，MV3DSAR系统的设计遵循如下基本理念：(1)轻量化，工业级无人机可挂载；(2)基线可重构，可以根据研究需求进行天线的灵活配置，从而实现不同的基线构型；(3)多极化，可通过天线和通道的模块化配置实现单极化与全极化模式。目前，单极化版本的MV3DSAR系统已经研制完成，全极化版本尚未进行集成和验证，为此，本文重点介绍当前的单极化MV3DSAR系统。

2.1 MV3DSAR系统构成

MV3DSAR系统的总体构成如表1所示，其主要由微小型SAR载荷、无人机平台及导航系统3部分组成，通过结构件进行固定和连接。SAR载荷及导航系统分布如图1所示，其中导航系统、SAR主机、存储模块和电池依次固定在结构件支架上方，SAR天线固定在结构件下方，其挂载于无人机平台后整个系统的照片见图2。

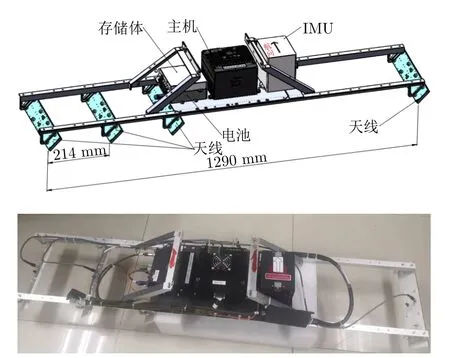
图1 MV3DSAR载荷示意图及实物图Fig.1 Schematic illustration and a photo of MV3DSAR payload

图2 MV3DSAR系统照片Fig.2 MV3DSAR system photo

表1 MV3DSAR系统总体构成Tab.1 The overall composition of the MV3DSAR system

2.2 Ku-SAR载荷参数

MV3DSAR系统最核心的是Ku波段阵列干涉SAR，该SAR载荷的主要参数如表2所示，其采用调频连续波体制，信号带宽为1.2 GHz，中心频率为15.2 GHz，重量为7.07 kg。目前版本MV3DSAR为单极化系统，等效的天线阵列通道数为4，也即一次飞行可以获得4幅相干的单极化SAR图像，后续将进一步扩展为全极化系统。系统天线支架结构长度为1.29 m(见图1)，有效长度为1.284 m，在有效长度内的0 mm,107 mm,214 mm,···,1284 mm处一共打有12排孔，用于固定天线并实现各种基线的灵活配置。

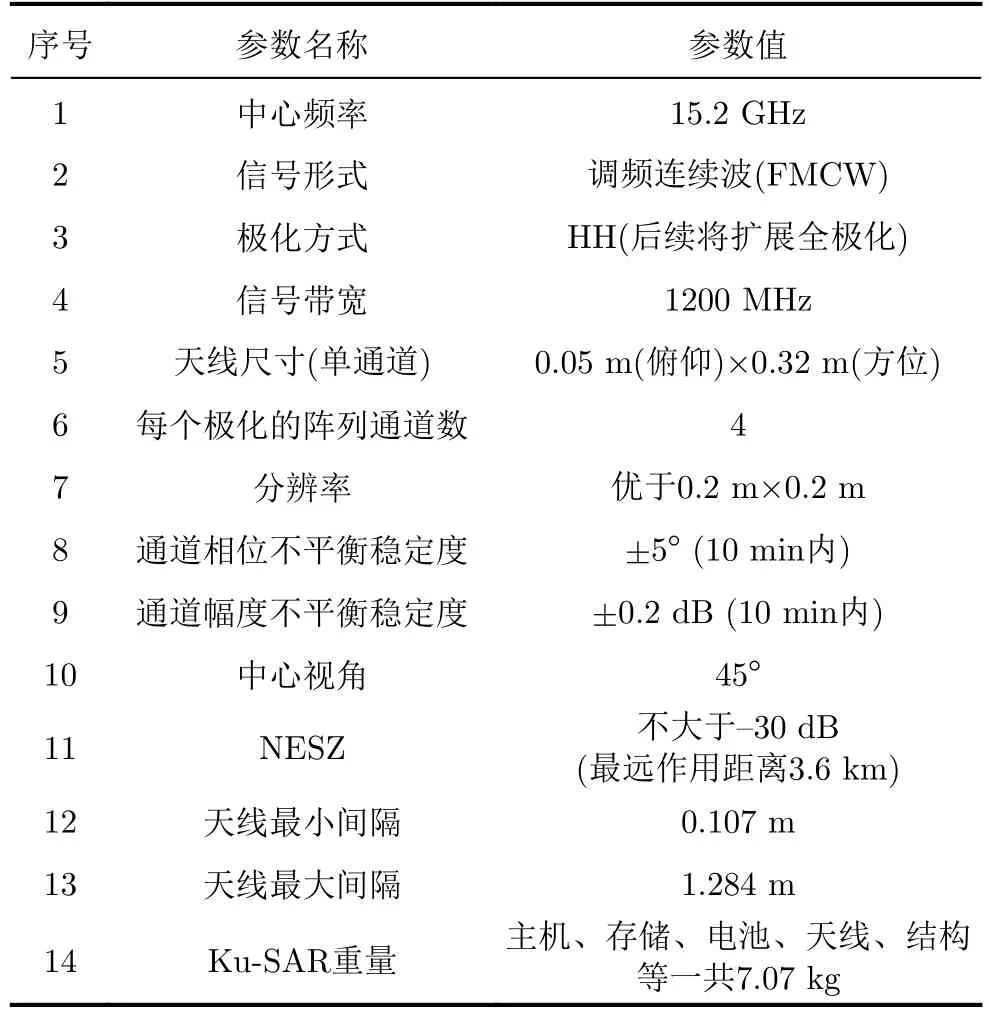
表2 Ku-SAR载荷参数Tab.2 Parameters of Ku-SAR payload

本系统将每个极化的阵列通道数设计为4，主要是考虑城区等实际场景中，叠掩数目大部分为2、小部分为3，叠掩数目大于3的情况占比非常小，为此可重点考虑叠掩数目小于等于3的情况[8]。对于单极化而言，4个通道将获得4个幅度、4个相位共8个观测量，而2个叠掩则包含2个斜高向位置、2个幅度、2个相位共6个待求量，因此理论上可以通过4幅相干图像三维成像达到区分两个叠掩的目的；而对于全极化而言，4组全极化相干图像可获得16个幅度、16个相位共32个观测量，理论上可以实现3个叠掩，即3个斜高向位置、12个幅度、12个相位共27个未知量的求解，从而可以满足大部分应用的需求，相关分析可参考文献[9]。需要说明的是，SAR三维成像所需空间相干观测数量的理论边界是一个十分复杂的问题，其与高程向分辨率、信噪比、三维成像方法等众多因素均相关，目前已有一些相关研究[8,10,11]但仍然存在很大的探索空间。尤其，在SAR微波视觉三维成像新方法下所需相干观测数量的理论边界，是一个值得探索研究的问题。

2.3 系统关键技术

MV3DSAR系统致力于小型化、经济化、高精度，在系统研制过程中突破的主要关键技术包括以下方面：

2.3.1 系统非线性误差处理技术

Ku-SAR系统采用调频连续波体制，由系统引入以及信号本身存在的非线性误差会对SAR成像结果产生影响。为此，Ku-SAR一方面采用预失真补偿手段提高激励信号线性度，另一方面通过在实验室采用延迟线定标方法与非线性处理方法对信号中的系统非线性误差项进行估计与校正[12]，使得校正后的信号非线性相位误差小于±0.2弧度，保证SAR成像结果满足指标要求。

2.3.2 高精度运动补偿数据获取技术

Ku-SAR系统搭载于轻小型运动平台，实际作业时平台可产生较大范围的运动误差及姿态变化，需对其进行精确测量，以便后续处理中进行补偿[13,14]。Ku-SAR系统集成了微型惯性测量单元(Micro Inertial Measurement Unit,MIMU)的控制模块以及GPS位置测量模块，结合导航系统将测量所得惯性导航数据与GPS位置数据融合，通过双捷联处理方法获取相对位置精度优于0.3 mm的运动误差数据，以满足成像处理的要求。

2.3.3 多通道一致性技术

Ku-SAR系统具有多个接收通道，以满足多极化、阵列干涉等任务需求。多通道信号之间延时、增益与相位的一致性是保证后续处理正确性的核心关键因素。Ku-SAR系统采用了基于低温共烧陶瓷(Low Temperature Co-fired Ceramic,LTCC)技术的多通道一致性设计、一致性定标回路与内定标设计、多通道间电磁屏蔽防串扰设计等有效方案[15]，使得系统通道间相位一致性达到±5°以内，图3为在实验室对系统多次重复上电测量得到的通道间相位差异结果，其包括了发射通道、接收通道、天线模拟环路的误差影响。相对于美国华盛顿大学于2019年在文献[16]中报道的通道间相位误差在0.4至1弧度内变化(±0.3弧度)而言，本系统通道间相位一致性明显更优，为获取有效数据提供了可靠保障。

图3 通道间相位差异实验室测量结果Fig.3 Laboratory measurements of phase difference between channels

2.3.4 小型化设计技术

Ku-SAR系统针对小型化设计需求，在系统的多个组成模块上均采用小型化设计方案[15,17]。其中，数字模块采用基于AXI (Advanced eXtensible Interface)总线的FPGA一体化设计技术，将控制、AD、DA、定时等多个模块集成在一个单片模块上，形成了集控制、处理等多功能为一体的高度集成化数字模块；在射频模块上采用LTCC工艺优化设计各个射频元器件的集成方案[18]，形成具有高集成度，高可靠性的射频模块。通过各模块的小型化设计，使得Ku-SAR系统达到较小的体积和重量，满足可搭载于工业级无人机的要求，便于实验任务的开展。

3 MV3DSAR校飞实验

为了验证MV3DSAR系统的基本性能指标和三维成像能力，我们于2021年12月1—2日在天津临港经济区开展了首次集成校飞实验。

3.1 实验对象

实验对象为临港商务大厦(如图4)，其由2栋15层塔楼及二层裙房组成，大厦区域占地面积22905.6 m2，楼高69.2 m，楼间距57.6 m，裙房高12.4 m、长105.6 m、宽72.4 m。该大楼结构具有一定的代表性，且周边比较空旷，便于进行定标器布设。

图4 天津临港商务大厦光学影像及照片Fig.4 Optical image of Tianjin Lingang Business Building

3.2 航线及基线设计

为兼顾航高限制、成像范围、最大不模糊高度、高程向分辨率以及三维成像最终结果的完整性，此次实验设计的飞行高度为400 m，波束范围内的成像幅宽为356.18 m。天线采用2发2收方式共形成4个等效天线相位中心，通过空间模糊函数的分析，优选了2种基线构型，如图5所示。图中，虚线表示结构件上打孔的位置，R1,R2为两个接收天线安装的位置，T1,T2为两个发射天线安装的位置，蓝色圆点表示等效天线相位中心的位置，两种模式的等效基线如表3所示。

图5 MV3DSAR校飞实验基线设计Fig.5 Baseline design of MV3DSAR flight experiment

表3 MV3DSAR校飞实验基线长度Tab.3 Baseline length of MV3DSAR flight experiment

在上述基线下，视角为45°时，观测矩阵的互相关特性以及空间模糊函数曲线如图6所示，最大不模糊高度和斜高向理论瑞利分辨率曲线如图7所示。可见，随着入射角的增加，不模糊高度逐渐变大，但同时瑞利分辨率也逐渐变差，且由于飞行高度较低，近距到远距的瑞利分辨率相差一倍以上，在三维成像处理及结果分析中需充分考虑入射角的变化。此外，模式2最大基线较长，理论的高程分辨率更佳，而模式1最小基线较短，可以获得更大的最大不模糊高度。然而，临港大厦69.2 m的高度已超过0.107 m最小基线对应的50 m左右的不模糊高度，给三维成像带来了额外的挑战。此外，由空间模糊函数图可见，两种模式分别在斜高向的±8.4 m,±28.4 m和±15.2 m,±21.6 m处存在高相关区域，需要在三维成像处理中采用有效手段来避免求解错误。综上可见，本MV3DSAR的三维成像处理存在很大的难度，本文第4节将通过引入图像视觉语义信息[19]等方法以获得较好的三维成像结果。

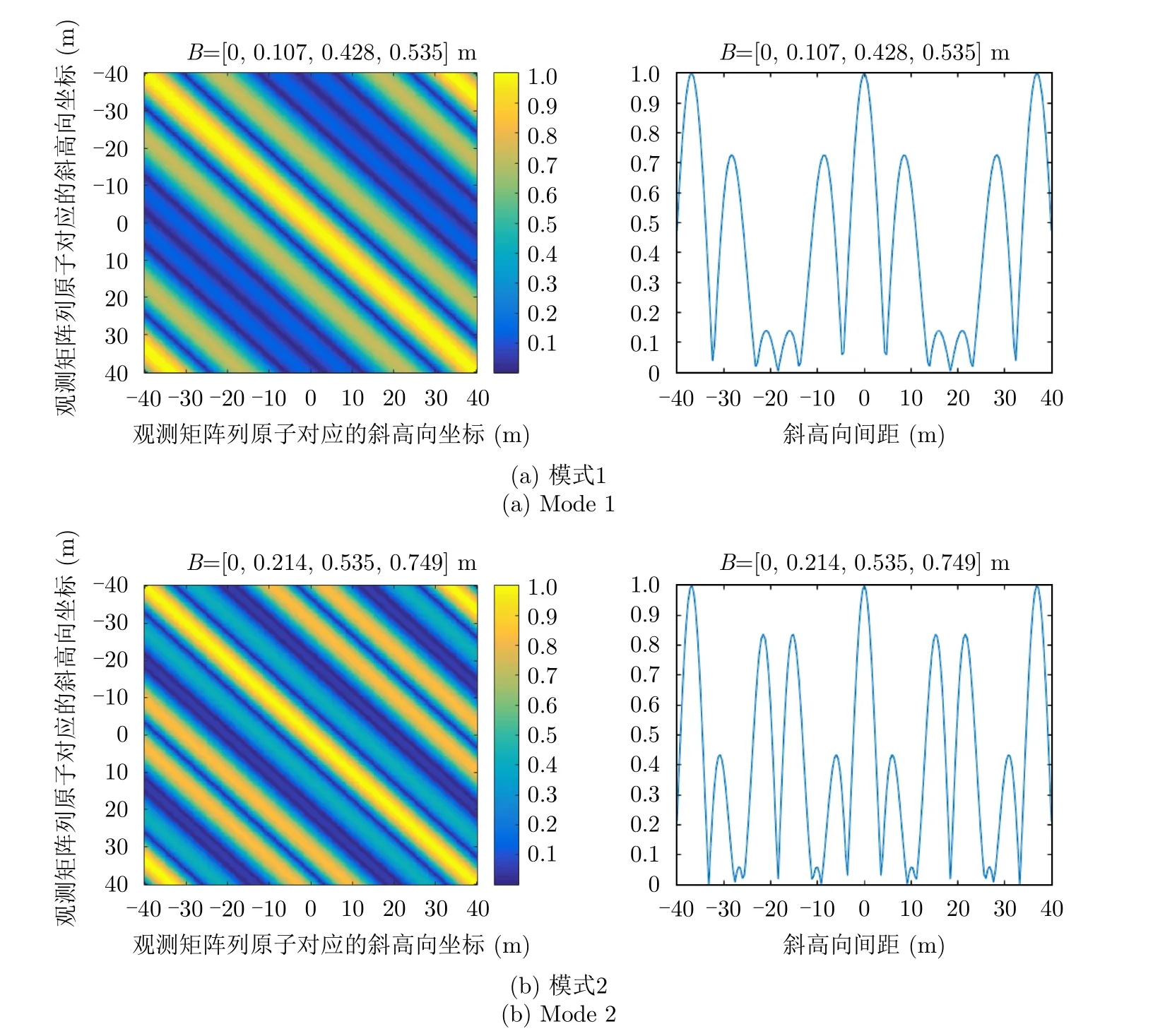
图6 观测矩阵互相关特性及空间模糊函数曲线Fig.6 Cross-correlation properties of observation matrix and spatial ambiguity function curve

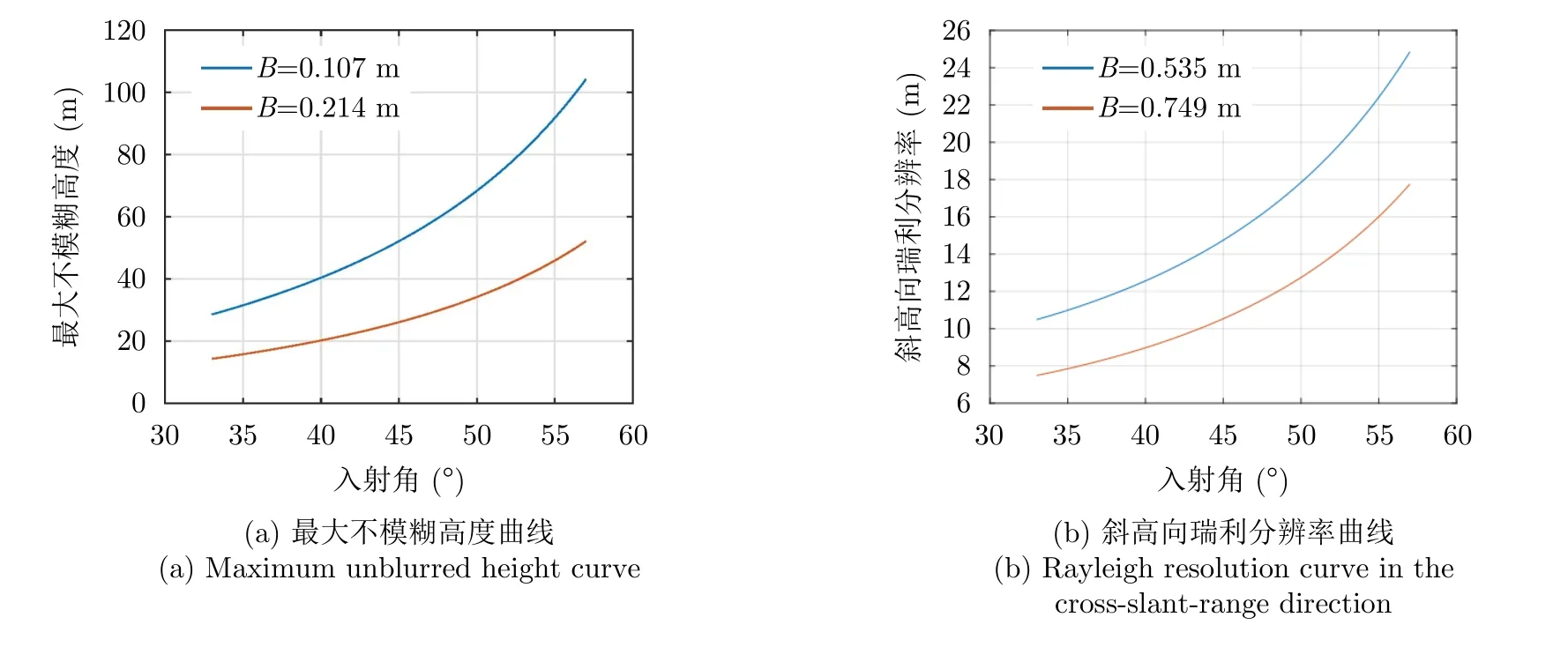
图7 最大不模糊高度及瑞利分辨率Fig.7 Maximum unblurred height and Rayleigh resolution

为了使获得的三维信息更加完整，同时为了支撑后续三维成像与散射机制结合等方面的研究工作，本次实验设计了8个方向的飞行航迹，记作ID0—ID7，如图8所示。

图8 MV3DSAR飞行航迹设计Fig.8 MV3DSAR flight path design

3.3 定标器布设

为了支撑成像质量评估，并支撑斜距、通道幅相误差等参数的标定，本次实验中定标器布设的现场照片及布设位置示意图见图9，布设有4个直径为0.3 m的龙伯球(记为L1—L4)，供8个飞行方向共用；4组由4个边长为0.4 m的三面角反射器拼合而成的四向角反射器组(记为J1—J4)，使得每个四边形航迹各有2组与之对应。采用差分GPS对上述定标器的三维位置进行了精确测量，三维位置测量精度优于5 cm。

图9 定标器布设示意图及现场照片Fig.9 Schematic illustration and photos of the calibrators

3.4 光学倾斜摄影及激光雷达数据采集

为了获得临港大厦区域的三维结构真值，从而为SAR三维成像结果的评价提供参考，实验同步利用无人机获取了光学倾斜摄影数据和激光雷达数据。其中激光点云数据高程精度优于2 cm，可为SAR三维成像结果的空间位置比较提供参考，激光点云的强度图和高度图见图10；光学倾斜摄影的影像分辨率优于2 cm，可提供丰富详细的建筑表面纹理信息，同时光学三维重建精度可以达到平面0.3 m/高程0.25 m，三维重建结果见图11，其可以辅助SAR二维/三维成像结果的分析和解译。

图10 激光点云结果Fig.10 Results of Lidar point cloud

图11 光学倾斜摄影结果Fig.11 Optical oblique photography results

4 MV3DSAR数据处理关键技术及初步结果

本次MV3DSAR集成校飞实验的主要目的是验证MV3DSAR系统在分辨率、通道幅相不平衡等方面的基本性能指标，并验证其进行三维成像的可行性。由于本次实验获取了2个模式8个方向的观测数据，数据量较大，且该系统只有4个通道，三维成像难度很大，因此相关研究和数据处理工作目前仍在进行之中。本节主要给出对于系统误差的标定方法与结果，以及初步的三维成像结果，以验证系统的基本性能和三维成像的可行性。

4.1 数据处理总体流程

针对多个观测方向获取的阵列干涉SAR数据，本文设计的总体处理流程如图12所示。首先对每个方向的4通道阵列干涉SAR原始回波数据进行二维成像处理；然后基于系统误差具有良好稳定性的前提，通过多个方向的SAR图像数据联合进行系统误差参数标定，包括系统延迟误差、通道幅度和相位误差，并确定和验证基线参数；随后进行干涉图像配准和相干性分析，为第三维成像提供基础；接着进行第三维成像处理，得到三维点云和点云对应的散射系数；最后对三维成像结果进行分析与评价，从而得到最终的三维成像结果和对三维成像性能的分析结果。

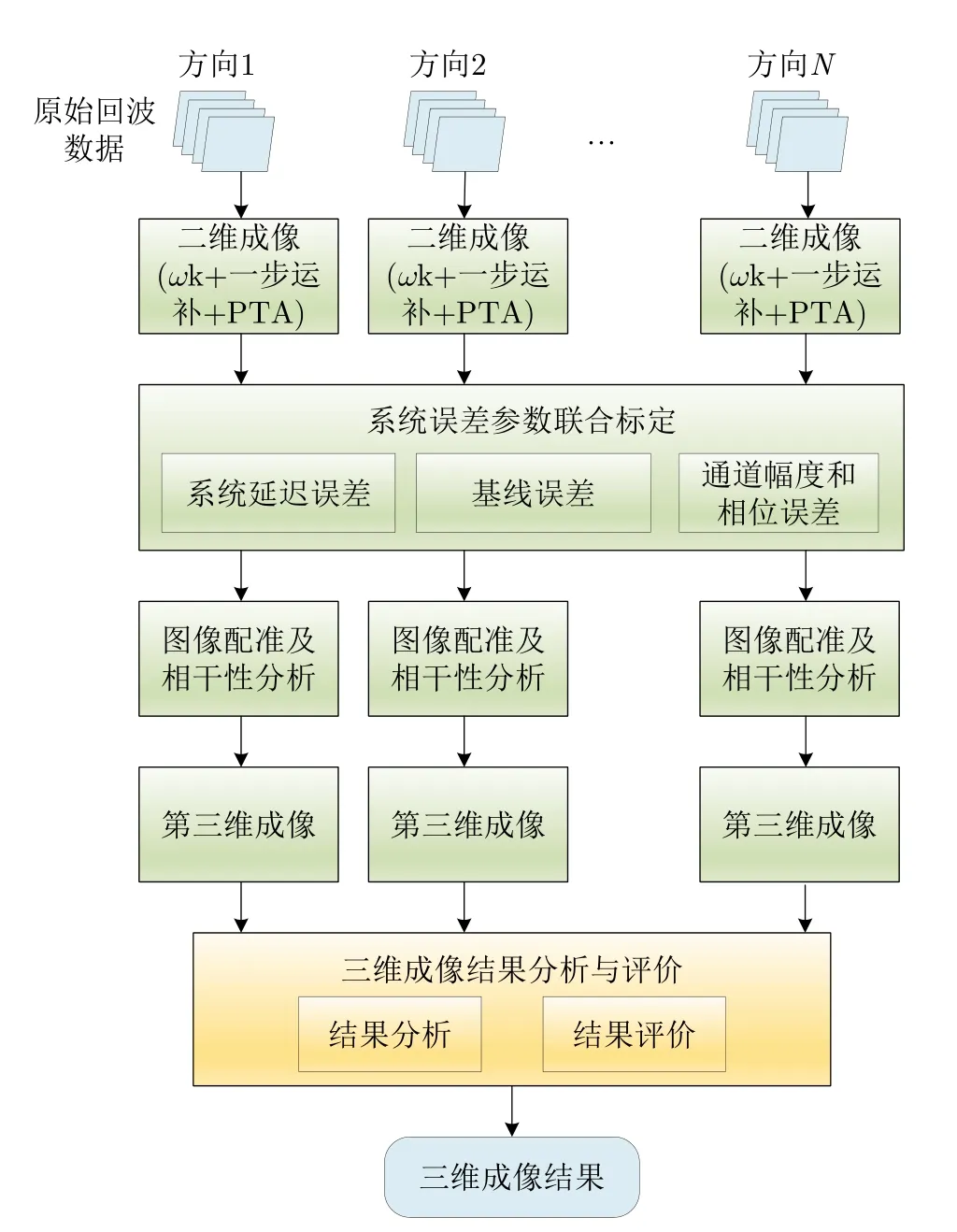
图12 MV3DSAR数据处理总体流程Fig.12 The overall flow of MV3DSAR data processing

在上述处理流程中，关键技术包括二维成像、系统参数标定、第三维成像这3个方面。二维聚焦的精度将直接影响图像信杂噪比，从而影响三维成像效果；同时二维聚焦精度也将影响图像语义信息的提取，对SAR微波视觉三维成像造成影响。系统延迟、基线、基线角、通道幅度/相位差异等参数对三维成像的求解结果有很大影响，尤其当通道数量较少时，三维成像求解的病态性更加严重，微小的参数误差就可能导致结果的严重偏差，甚至使得三维重建失败，因此，系统参数的标定至关重要。第三维成像则是本系统数据处理的核心环节，直接决定三维成像的成败。为此，后续小节将重点针对上述关键步骤进行处理方法的阐述并给出初步处理结果。

4.2 二维成像

通过航迹解析，8个方向航迹(ID0—ID7)与参考匀速直线航迹的偏离程度如图13所示，飞行方向上由于非匀速运动引起的偏离在2 m以内，垂直飞行方向航迹控制在1 m以内，且大部分控制在0.4 m半径的“管道”内，航迹控制较好。通过姿态数据解析，8个方向飞行的姿态数据测量结果如图14所示，横滚角变化在3°以内，偏航角变化在2°以内，俯仰角变化在4°以内，姿态变化相对较大。根据上述航迹和姿态数据以及本系统参数，按照文献[20]的理论公式，以只进行一步运补、不考虑合成孔径内运动误差补偿的方式，分析了目标点实际高度与成像参考高度差为70 m时，运补残余误差给模式1最长基线的两个通道带来的干涉相位误差。数值计算结果表明，干涉相位误差不超过2.5°，如将该相位偏差当成随机相位噪声进行简单核算，运补残余误差引起的去相干效应仅使相干系数降低0.002，基本可以忽略。然而对于聚焦而言，孔径内的运补残余误差引起的二阶以上相位误差超过了12弧度，必须进行孔径内运动补偿以提高聚焦质量。此外，分析表明较大的姿态变化引起的多普勒中心频率变化最大达到了120 Hz，超过了55 Hz左右的多普勒带宽，也需要在成像处理中根据中心频率的变化进行处理频带和运动误差计算参考的调整。

图13 航迹与参考匀速直线航迹的偏离程度Fig.13 Difference between actual flight path and reference track

图14 姿态测量数据随时间的变化曲线Fig.14 Variation curve of attitude measurement data with time

因此，我们首先在实验室采用进口的意大利RPS关节臂测量机(RPS EV07)精确标定了天线相位中心(图15中的R2,R1,T2,T1)和导航测量单元位置(图15中的T)的相对关系(见表4)，并根据飞行过程中的姿态测量值，解算得到每个通道数据所对应的航迹数据。随后，各个方向均采用平行的直线航迹为参考航迹，地面高度为参考高度，采用ωk算法结合一步运补及孔径内残余运动误差补偿(PTA)的方法[21,22]进行成像处理。其中，一步运补在距离向压缩后的距离和方位时域进行，不同距离门根据中心频率的变化采用不同的参考斜视角进行运动误差的计算和补偿；PTA是在二维压缩后进行逐点方位向补偿处理，以每个像素点为中心，截取方位向64个相邻像素组成局部信号，变换到方位频域后进行孔径内残余运动误差补偿，补偿时顾及了中心频率的变化，继而进行傅里叶逆变换得到补偿后的时域信号，取对应像素点为该像素的最终成像结果。

图15 天线相位中心相对位置关系测量示意图Fig.15 Schematic diagram of the relative position of the antenna phase center

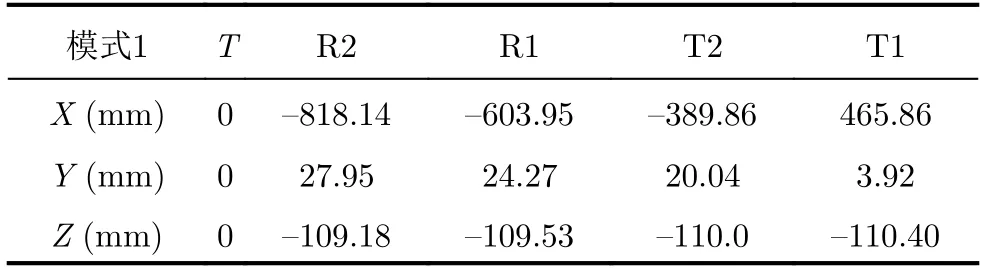
表4 天线相位中心相对位置Tab.4 Relative position of antenna phase center

以ID0为例，给出龙伯球和角反射器的分辨率测试结果如表5和图16，可见图像分辨率能够满足设计指标，且距离向分辨率相比理论值展宽小于1.015，方位向分辨率在方向图加权下的展宽小于1.08，点目标的峰值旁瓣比和积分旁瓣比与理论值的偏差分别小于0.8 dB和1 dB，图像聚焦质量良好。将得到的每个方向成像结果，根据入射方向排列如图17所示，可见在不同角度下，龙伯球和四向角反射器组均得到了较好的呈现，可以支撑参数标定等处理；同时临港商务大厦区域均在图像的有效范围内，说明了SAR数据获取的有效性。

图16 龙伯球和三面角反射器点目标曲线Fig.16 Luneburg-Lens reflector and trihedral corner reflector point target curve

图17 8个方向临港商务大厦区域成像结果Fig.17 Imaging results of Lingang Business Building in eight directions

表5 定标器分辨率Tab.5 Resolution of the calibrators

4.3 系统延迟误差标定

为了获得准确的干涉和三维成像结果，由系统延迟造成的斜距误差是首先需要标定的量。由于基于龙伯球半径和GPS测量值计算得到的龙伯球位置对应于龙伯球球心，而雷达波与龙伯球发生作用的点位于龙伯球表面处，存在一定的偏差，为此，我们重点采用角反射器组进行斜距误差标定。此外，为了降低系统参数标定对人工定标器布设和真值测量的依赖，本文研究了有控制点和无控制点两种系统延迟误差标定的方法。此处以模式1的T2R1通道数据为例，给出处理方法和结果。

有控方法以角反设器为控制点，以角反射器测量的三维位置真值和航迹位置来计算每个控制点的斜距，并与该点在图像中像素位置(升采样512倍后得到)计算得到的斜距做差得到斜距误差，进而拟合出斜距误差随距离向像素坐标的变化曲线，后续处理使用拟合的斜距误差曲线修正数据的斜距。

无控方法不需要角反射器三维位置真值，采用角反射器(或其他不同角度观测均能呈现为强散射点且散射中心位置相同的目标)作为连接点，基于8个角度观测的图像数据，通过归一化距离多普勒(RD)方程[23]联立，同时进行连接点三维位置、斜距误差等参数的求解。无控方法求解的最优化目标函数如下：

其中，i为观测航迹的序号，j为连接点序号，ΔR0和ΔR1为斜距误差函数的常数项、一次项系数，fDi为第i个观测成像采用的多普勒中心频率，Pj为待求的连接点三维位置，Sij为第j个连接点在第i个观测图像中像素位置所对应的SAR天线相位中心三维位置，Vi是第i个观测成像时采用的参考匀速直线运动速度，xij是第j个连接点在第i个观测图像中的距离向像素坐标。

表6给出了两种方法得到的斜距误差标定结果，图18给出了两种方法得到的斜距误差曲线和8个观测中根据角反射器位置和SAR位置计算的斜距差异的结果。可以看到斜距误差呈现近端小、远端大的趋势，有控和无控两种方式得到的斜距误差曲线比较一致，该线性变化是由于SAR系统在发射和接收调频连续波的整个系统环路上引入的色散效引导致的。表7给出了利用有控方法得到的斜距误差修正后，再进行多角度RD方程联立得到的定标器三维位置和测量三维位置的差异，以及无控方法得到的定标器三维位置和测量三维位置之间的差异。由表7可见，有控方法下4个角反射器的三维位置中误差为4.7 cm，无控方法下三维位置中误差为10.6 cm。上述结果一方面侧面验证了角反射器位置测量精度能够达到厘米级；另一方面也表明，在多角度观测下，若无定标点三维位置真值，也可以通过多角度联立求解得到良好的三维位置计算结果和斜距误差标定结果。

图18 斜距误差随距离向的变化曲线Fig.18 Variation curve of slope distance error with distance direction

表6 斜距误差标定结果Tab.6 Calibration result of slope distance error

表7 两种方法的三维位置偏差(厘米)Tab.7 3D position deviation of the two methods (cm)

4.4 基线长度及基线角

MV3DSAR系统采用一个5 mm厚度的铝质金属结构件来保证天线安装固定后的稳定性，通过在实验室对天线相对位置的精确测量(图15)，基线长度精度可以达到1 mm。基线角是通过姿态测量数据和天线相位中心相对位置矢量，计算得到各通道航迹后拟合得到成像参考匀速直线航迹，再通过各个通道参考匀速直线航迹之间的空间角度关系来得到的。本系统的姿态测量精度为0.02°，通过仿真[20,24]，在本实验参数下引起的高程误差为0.2 m以内，故此处直接采用测量值。本文4.5节的相位误差估计结果，也从侧面证明了采用测量基线和基线角的合理性。表8以模式1的ID3为例，以T2R2的等效天线相位中心为参考，给出了基线和基线角的数值。

表8 基线与基线角(T2R2为参考通道)Tab.8 Baseline and baseline angle (T2R2 channel for reference)

4.5 通道幅相误差标定

在斜距、基线、基线角参数确定后，进一步进行通道幅度和相位误差标定[25,26]。其中，幅度误差的标定相对简单，通过提取点目标的峰值并计算各个通道定标点目标峰值差异，得到结果如表9所示，可见幅度不平衡稳定度能够满足优于±0.2 dB的设计指标。

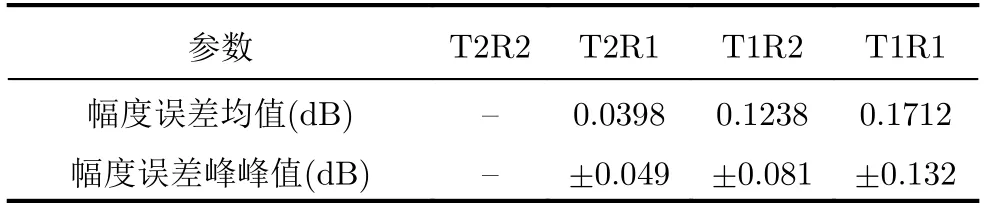
表9 通道幅度误差标定结果(T2R2为参考通道)Tab.9 Calibration result of channel amplitude error(T2R2 channel for reference)

相位误差的标定通过提取定标器峰值相位，计算与参考通道的峰值相位差，并与根据基线、基线角、目标三维位置真值计算得到的相位差真值进行比较得到。

设点目标点实测三维位置为P:(x,y,z)T，根据其在图像上的像素位置(升采样512倍后)，得到目标被照射的方位时刻所对应的SAR天线相位中心位置分别为ST1R1,ST1R2,ST2R1,ST2R2。以T2R1和T2R2这组干涉图像对为例，可以求得目标P到对应天线相位中心的两个斜距真值分别为

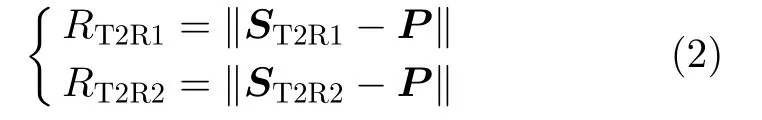
由此可得到目标的实际相位差为

其中，λ为波长。

分别根据目标点在T2R1和T2R2复数图像上的位置，提取升采样后目标峰值处的相位φT2R1和φT2R2，两者相减即可得到干涉相位

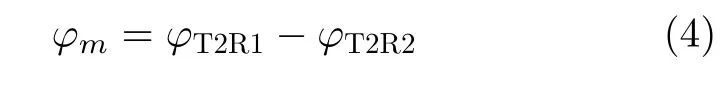
将图像干涉相位和实际相位差相减并解缠绕，即可得到相位误差为

其中，wrap(·)表示相位解缠。

通过上述计算并画出每个目标点在每个干涉图像对中的相位误差计算结果，就可以分析相位误差的规律。通过分析发现，发射通道相同时，两个接收通道之间的相位误差比较恒定，如图19所示，其不随距离变化，以R2接收通道为参考，R1与R2的相位差平均值为44.68°，变化在5°以内；去除R1和R2之间的相位差异后，T1和T2之间的相位差异呈现随距离向的变化，如图20所示，线性拟合后的常数项和线性项如表10所示，拟合后的残余相位如图21所示。可见，除了个别点外，残余相位在±5°以内，满足系统设计指标。其中，发射通道之间随距离向变化的相位误差，是由两个发射通道发射通路上引起的不同相频特性导致。此外，由于本次实验中，每个ID数据获取时SAR单独开关机，使得每次成像的初相有所不同，故存在±5°的残余相位是与图3的实验室测量结果相吻合的。

表10 通道相位误差标定结果Tab.10 Channel phase error calibration results

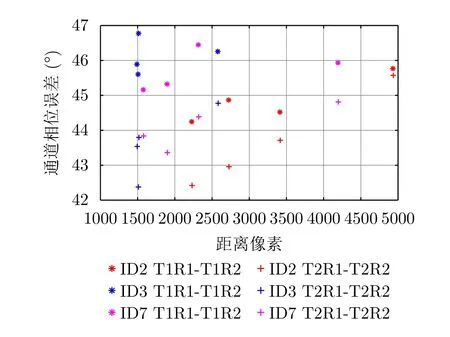
图19 接收通道间相位误差与距离向的关系Fig.19 The relationship between the phase error of the receiving channels and the slant range

图20 发射通道间相位误差与距离向的关系Fig.20 The relationship between phase error of the transmit channels and the slant range

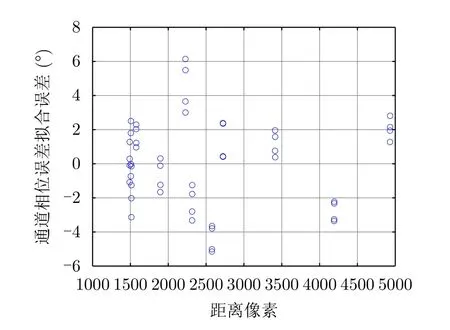
图21 发射通道间相位误差与拟合直线的偏差Fig.21 Deviation of phase error between transmit channels and the fitted straight line

4.6 图像配准及相干性分析

干涉SAR图像的配准精度要求到亚像元级，本论文采用粗配准和精配准结合的方式进行干涉复图像的高精度配准[27,28]。首先在21×21的搜索窗内按行列以整像元为单位逐个计算匹配窗与数据窗之间的相干系数，选取相干系数最大位置作为同名点位置，由此得到像元级的粗配准结果。然后对辅图像进行10倍升采样，再利用类似的方法得到亚像素级的精配准结果。下面以ID3为例，给出了4个通道图像配准后两两计算相干系数的结果(图2 2、图23)和去平地后的干涉相位结果(图24)。可见，同一个通道发射、不同通道接收的图像之间，相干系数统计曲线峰值可以达到0.988以上；不同通道发射、不同通道接收的图像之间，相干系数统计曲线峰值也可以达到0.96以上，良好的相干性为后续三维成像处理奠定了基础。

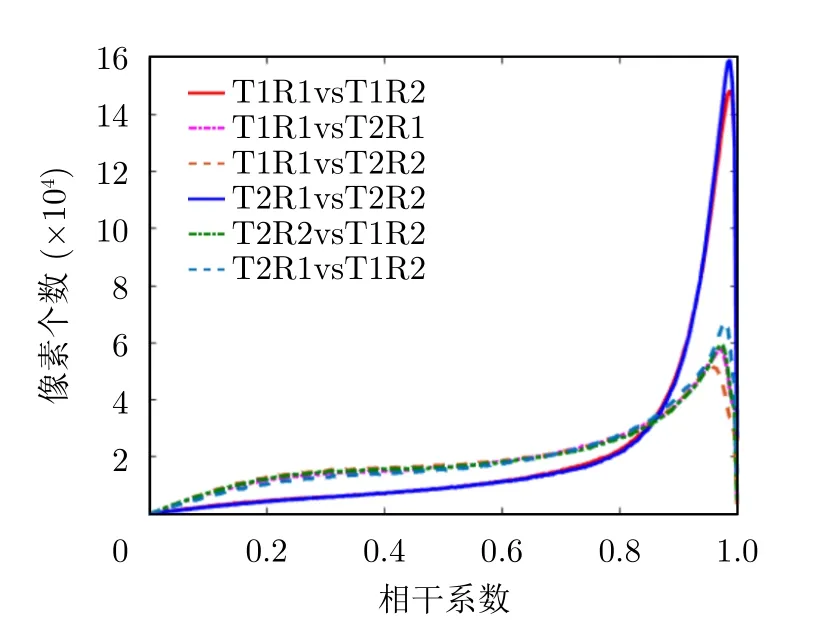
图22 相干系数统计曲线Fig.22 The statistical curve of coherence coefficient

图23 相干系数图Fig.23 Coherence coefficient map

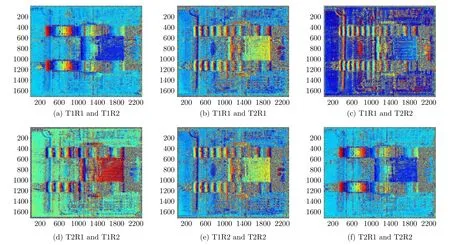
图24 去平地后的干涉相位图Fig.24 Interferometric phase diagram after removing flat-ground phase

4.7 三维成像方法及初步结果

在完成前述斜距误差及通道幅相误差标定和高精度图像配准的基础上，我们接着开展第三维成像处理工作。正如3.2节所述，临港商务大厦高69.2 m，超过了微波视觉三维SAR系统的最大不模糊高度，因此传统方法重建得到的三维点云存在严重模糊，难以进行坐标转换进而得到目标三维结构。并且，由于本系统仅有4个通道，传统SAR三维成像算法在较少观测次数下成像性能较差。

为了解决上述问题，项目组将SAR图像视觉信息中获得的几何信息作为约束，融入阵列SAR三维成像处理的数学模型中，得到了初始的三维点云[19]。其中，为了从SAR图像中提取能够辅助三维成像的结构信息，可以手动或自动地对图像进行语义分割[29]，也有研究者提出了面向阵列干涉SAR点云规则化渐进式建筑立面检测的方法[30]，可以与三维成像迭代应用[31]。当然，从SAR图像中自动进行准确的语义分割和几何结构提取具有很大难度，相关研究尚不成熟，为此，图25展示了利用ID3以及ID7两个角度图像手动得到的建筑物立面分割结果。利用这一信息，可以从如下两个方面辅助SAR三维成像处理。

图25 SAR图像建筑几何结构分割结果Fig.25 Segmentation results of building geometry in SAR image

第一，SAR图像是目标三维模型在二维成像平面的映射，SAR图像中属于同一几何结构的像素，重建得到散射点的三维空间分布也存在相应几何关系。基于这一规律，可以对三维重建的解空间进行约束，能够提升在较少观测次数下的三维重建质量。具体的，首先在没有结构约束的情况下进行三维重建，得到初始三维点云；之后，针对从二维图像中检测到的隶属于同一几何结构(直线、平面等)的散射点三维重建结果，拟合其在三维空间的分布；最后，利用拟合得到的散射点空间分布结合信噪比的大小来形成对解空间大小的限制，如信噪比大(如超过20 dB)则解空间范围可放大，而信噪比小则解空间被限制到拟合空间分布附近较小的区域；随后在约束后的解空间范围中迭代求解三维位置，提升少数观测情况下的三维重建质量。式(6)分别展示了空间中的平面方程，以及几何参数求解的优化目标函数，其中：T为根据经验设定的距离

阈值；sign(*)为符号函数；d ist(i,P)表征散射点i到平面P的距离，在实际计算中可以利用随机抽样一致性(RANSAC)方法进行计算，能够解决观测次数少、信噪比低导致的杂点比例过高问题；r为斜距轴，s为垂直斜距的斜高轴，x为方位轴，A1,B1,C1,D1为平面参数，N为点的数量。

第二，结合图像语义信息提出了基于三维点云聚类的解模糊方法[32]。具体的，由于临港商务大厦高度超过了69 m，远超系统的最大不模糊高程，因此一定会存在斜高向模糊现象，如图26(a)所示。利用图像分割得到的建筑物立面信息，将图像分割后具有相同标签的像素进行协同处理，这些像素重建得到的散射点属于同一结构。对隶属于同一结构且存在模糊的三维点云进行空间聚类，基于目标结构的连续性判断各类别点云的模糊数，进而实现三维点云解模糊，解模糊之后的点云见图26(b)。

图26 重建三维点云解模糊前后结果对比图Fig.26 Comparison of results before and after 3D point cloud deblurring

以ID3和ID7两个角度的观测为例，在进行前述处理后得到的三维成像结果如图27所示。可以看出，针对临港商务大厦的不同角度观测所获取的散射信息具有显著差异，两个角度散射特性一定程度上能够互补。另外需要指出，如实验结果所呈现，在建筑物底角部分，由于存在较为复杂的多次散射，重建散射点杂散程度高，后续仍需进一步探索和精化处理。关于多径效应下SAR三维成像方法的研究可参考文献[33]。

为了验证系统的三维成像质量，项目组利用实验中同步获取的高精度激光点云作为参考真值，对三维重建的结果进行定量化评价。以下从三维成像分辨率、重建精度以及重建完整性3个角度开展定量化评价工作。

如图7所示，微波视觉三维SAR系统的斜高向瑞利分辨率随观测视角变化，最优约为7.5 m。根据激光点云测量结果可知，临港商务大厦层高约5 m，考虑入射角后在斜高向的投影仍然小于7.5 m，但是从图27的三维重建结果中可以看出同一楼层的散射点得到了分辨。一方面，相邻楼层的散射在二维图像的距离向上跨越了多个距离门，得到了分辨；另一方面，本实验所采用的斜高向三维成像处理算法具备超分辨能力，在工程实践中能够实现约10倍的超分辨率成像，即能够区分斜高向间隔小于1 m的散射点，因此即使落入相同距离门，在高信噪比条件下也具备一定的分辨能力。

图27 临港商务大厦三维重建结果Fig.27 3D reconstruction results of Lingang Business Building

针对三维重建精度，根据ID3和ID7数据重建得到的三维点云，建筑物高度估计约为66.7 m，而激光点云测量得到的建筑物高度为69.2 m，高度测量误差约2.5 m。在具备激光点云真值的情况下，定义三维重建精度和完整性如下[19]：

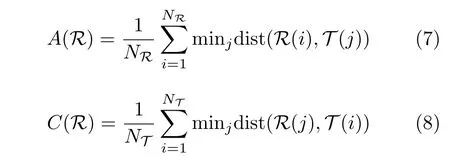
其中，R,T分别代表重建三维点云和激光点云，NR和NT为对应包含的散射点数量，R(i),T(j)分别为重建结果和激光点云的第i个和第j个散射点，dist(*)代表两个散射点之间距离度量。为分析上述指标，针对临港商务大厦，将多角度重建的结果和激光点云进行了配准处理，配准后的结果如图28所示。根据式(3)和式(4)得到结果如表11所示，各角度重建精度接近，满足预期；而重建完整性受到不同观测角度遮挡情况的不同，存在较大差异，融合后的结果完整性有显著提升。

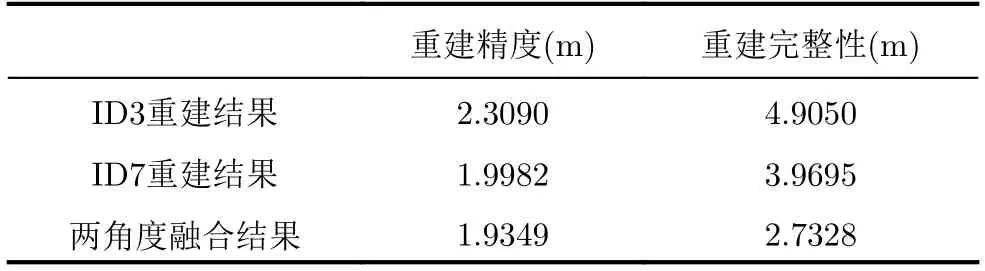
表11 三维点云的精度及完整性Tab.11 Accuracy and completeness of 3D clouds

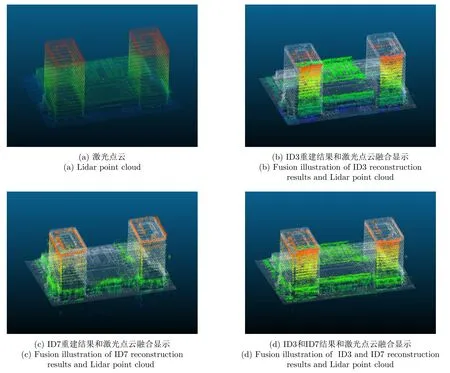
图28 临港商务大厦SAR三维成像点云与激光点云Fig.28 SAR 3D reconstruction results and Lidar point cloud of Lingang Business Building

综上，临港商务大厦的三维结构得到了较好的重建，验证了MV3DSAR系统的三维成像能力。后续将进一步开展各个角度的三维成像处理，并进行各个角度信息的融合和多角度联合处理，在三维几何坐标系下实现目标散射信息更全面的表征[9]。

5 结束语

本文介绍了微波视觉三维SAR实验系统(MV3DSAR)的组成、系统参数和研制关键技术，并给出了该系统首次集成校飞实验的模式设计、航线设计和定标器布设情况，最后给出了系统误差标定的方法和结果，并给出了初步的三维成像结果，验证了该系统的基本性能和三维成像能力，可以为后续SAR微波视觉三维成像理论方法研究和验证提供支撑平台。

在国家自然基金重大项目支撑下，项目团队后续将进一步开展基于微波视觉的SAR三维成像方法研究，并继续开展该实验数据的处理和指标评估工作，推动SAR三维成像技术的应用。

致谢本次实验得到了中国科学院空天信息研究院齐鲁研究院任天宇博士团队在光学和激光雷达数据获取方面的大力支持，空天院刘忠胜老师、韩冬、董书航、王沐涵、刘子楠同学在实验开展和现场实施方面的有力支撑，以及空天院苏州研究院张柘、李杭、金燕副研究员、彭凌霄助理研究员，杜邦、施睿哲、吕泽鑫等同学在性能仿真、图像配准等方面的工作支撑，在此一并表示感谢。