面向阵列InSAR点云规则化的渐近式建筑立面检测

王 伟 许华荣 魏含玉 董秋雷

①(周口师范学院网络工程学院 周口 466001)

②(厦门理工学院计算机与信息工程学院 厦门 361024)

③(周口师范学院数学与统计学院 周口 466001)

④(中国科学院自动化研究所 北京 100190)

⑤(中国科学院大学人工智能学院 北京 100049)

1 引言

干涉合成孔径雷达(Interferometric Synthetic Aperture Radar,InSAR)技术由于具有全天时全天候高分辨率成像的优势，在地形测绘、数字化城市建模中具有重要的应用价值。层析SAR或阵列In-SAR三维成像技术[1–3]可通过在高程向获取的三维几何与散射信息实现目标三维结构的重建，进而可有效克服传统InSAR技术中的叠掩、透视缩短等问题，近年来倍受研究者的关注。在实际中，对于具有多平面结构特征的城市建筑，由于孔径或天线装置设计、信息获取与相关计算误差等因素的影响，层析SAR或阵列InSAR三维成像技术获取的初始空间点通常存在以下问题：(1)较为稀疏或部分结构对应的空间点缺失而不足以表达其完整的结构；(2)与真实结构存在偏差或噪声点较多而需要进行规则化处理。

一般而言，空间点稀疏问题可通过对其进行上采样的方式解决，然而，当前相关算法[4]往往存在难以对缺失空间点进行补全、噪声点易被同时上采样、空间点数量较大时较为耗时等问题而不易获得较好的结果。此外，对于以空间点融合或结构检测与推断为目的的算法[5,6]，由于其对初始空间点的精度要求较高，因而在初始空间点包含较大噪声时难以保证较好的性能。在此情况下，利用多模型拟合算法(通过分析局部空间点的分布形态确定其是否位于同一平面)从初始空间点中检测出尽可能多的可靠建筑平面将对建筑初始空间点的规则化以及建筑完整结构的推断具有重要的作用(如利用建筑立面补全位于其上的缺失空间点、以建筑立面为基础推断建筑长方体结构等)。然而，当初始空间点数量较多且所包含噪声较大时，当前多模型(如平面)拟合算法[7,8]不但效率较低，而且可靠性较差(如利用随机抽样方式生成候选平面时较为耗时且易丢失真实平面、全局式平面优化时由于参数与邻域关系不易控制而导致较大的错误等)。

为了解决以上问题，本文通过冗余线段与直线剔除、线段可靠性度量与检测过程优化等方式对前期所提算法[9]进行了改进，提出一种面向阵列InSAR点云规则化的渐近式建筑立面检测算法(Progressive Building Facade Detection,PBFD)；本文算法通过将平面检测问题转化为空间点在地面投影图中的多阶段线段检测问题进行求解并利用在当前阶段检测的线段与结构先验构造后续线段检测空间，可有效克服阵列InSAR点云规模及噪声的影响，快速从中检测出较多的可靠建筑立面。

2 相关工作

建筑点云中的立面检测是数字化城市建模、增强现实等应用的基础性工作，在建筑点云包含未知数量的立面时，适于单平面检测的RANSAC算法[10]往往难以产生较好的结果；在此情况下，多模型拟合算法通常可采用候选平面生成(如随机采样空间点拟合平面)、平面优化(如冗余平面剔除)等步骤从中检测出较多的平面；例如，贪心或聚类方式的多平面检测算法[11–15]通过不断探测具有最大内点(满足指定空间点与平面之间距离度量的空间点)的平面并移除相关内点、利用相邻平面的相关性剔除冗余平面等过程实现多平面的检测。此类算法虽然可获得相对较好的效果，但由于未充分考虑不同平面之间的关联、候选平面生成可靠性与效率较低等问题，在许多场合(如空间点包含较大噪声时)下不易获得全局部最优解。

相对而言，通过融合相邻平面一致性、模型复杂度等约束或规则化项的全局式平面检测算法可有效提高平面检测的整体一致性；例如，Isack等人[16]提出了一种基于能量最小化的多模型拟合方法，其通过在能量函数中融合数据点间的平滑性约束及整体模型复杂度惩罚而提高平面检测的可靠性；Pham等人[17]将基于“随机聚类模型”[18]的候选模型生成与基于模拟退火的模型优化进行融合并以相互增强的方式交替地完成两个过程，有效提高了多模型拟合的精度；Barath等人[19,20]则通过在模型参数空间更新模型类别集或通过迭代模型生成、冗余模型滤除、模型优化等步骤提高整体模型拟合的性能。最近，研究者利用可提取不同层次特征的深度神经网络对平面拟合问题进行求解并获得了较好的结果；例如Brachmann等人[21]通过训练深度神经网络为数据点分配相应的采样权重以抑制外点，进而有效提高了基于RANSAC算法的候选平面生成效率；Kluger等人[8]则利用深度神经网络持续更新候选平面生成时的采样概率以生成可靠的候选平面，进而有效提高了整体平面检测的可靠性。事实上，此类算法虽在空间点较为稀疏的情况下可获得较好的效果，但在空间点较多且包含较大噪声时，其候选平面生成与平面优化的效率与可靠性均难以得到保证。

针对大规模空间点中的平面检测问题，分阶段或渐近式的算法通常更有利于提高整体效率与可靠性；例如，Shahzad等人[22,23]通过空间点密度估计、建筑立面法向量估计、建筑立面分割等步骤从TomoSAR点云中检测较大区域建筑立面的检测。然而，由于相关步骤(如基于密度的聚类)较为耗时，算法的整体效率并不高；此外，由于算法缺乏对潜在建筑立面的探测，因而最终获取的可靠建筑立面数量也较少。

3 PBFD算法原理

为提高大规模带噪阵列InSAR点云中建筑立面检测的效率与可靠性，PBFD算法通过将初始点云投影至地面、渐近式线段检测等步骤实现建筑立面的检测，其基本流程如图1所示。

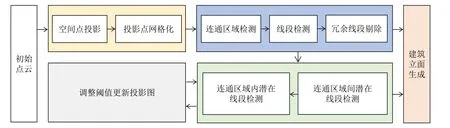
图1 PBFD算法流程(黄:投影图生成，蓝:主线段检测，绿:潜在线段检测)Fig.1 Flowchart of the PBFD method (yellow:projection map generation,blue:main line segment detection,green:potential line segment detection)

PBFD算法的主要步骤描述如下：

步骤1 投影图生成(将初始空间点投影至地面并设定阈值生成投影图以从中检测连通区域)。

步骤2 主线段检测(利用线段检测、合并与分组等方式在连通区域内检测线段)。

步骤3 潜在线段检测(根据已检测线段与结构先验的约束在未遍历的连通区域内检测线段，若无法检测出新线段，则转至步骤5)。

步骤4 投影图更新(降低阈值以更新投影图，若生成较大尺寸的连通区域则转至步骤3，否则转至步骤5)。

步骤5 建筑立面生成(根据检测到的线段及其对应的空间点生成建筑立面)。

PBFD算法的主要创新之处如下：

(1) 将大规模建筑立面检测问题转化为规模可控的线段检测问题，提高了问题求解的灵活性。

(2) 利用融合结构先验的渐近式多线段检测方法提高了线段检测的精度与效率。

(3) 利用融合几何信息、结构先验与结构复杂度的直线可靠性度量提高了直线检测的可靠性。

下文对以上步骤中的关键环节进行描述。

3.1 投影图生成

在理想情况下，对于位于同一建筑立面上的空间点，不但其中的多个空间点投影至地面同一位置(或同一位置较小邻域内)的概率较高，而且所有空间点在地面上的投影(下文简称地面点)也较为集中并沿直线分布；相对而言，位于非建筑立面上的空间点对应的地面点则较为分散。在实际中，由于噪声点的存在及计算偏差的影响，将初始空间点投影至地面后，根据地面点的横纵坐标的范围则可构建由地面点构成的初始投影图；如图2(c)所示，在初始投影图中，与建筑立面对应的大多数地面点(约94%)与数量较多的空间点相对应(即多个空间点投影至同一地面点)且聚集成矩形状甚至点状(通常由稀疏空间点投影所致)的连通区域，而与非建筑立面对应的地面点则与数量较少的空间点(如空间点与地面点一一对应)相对应且分散于建筑立面对应地面点的附近。

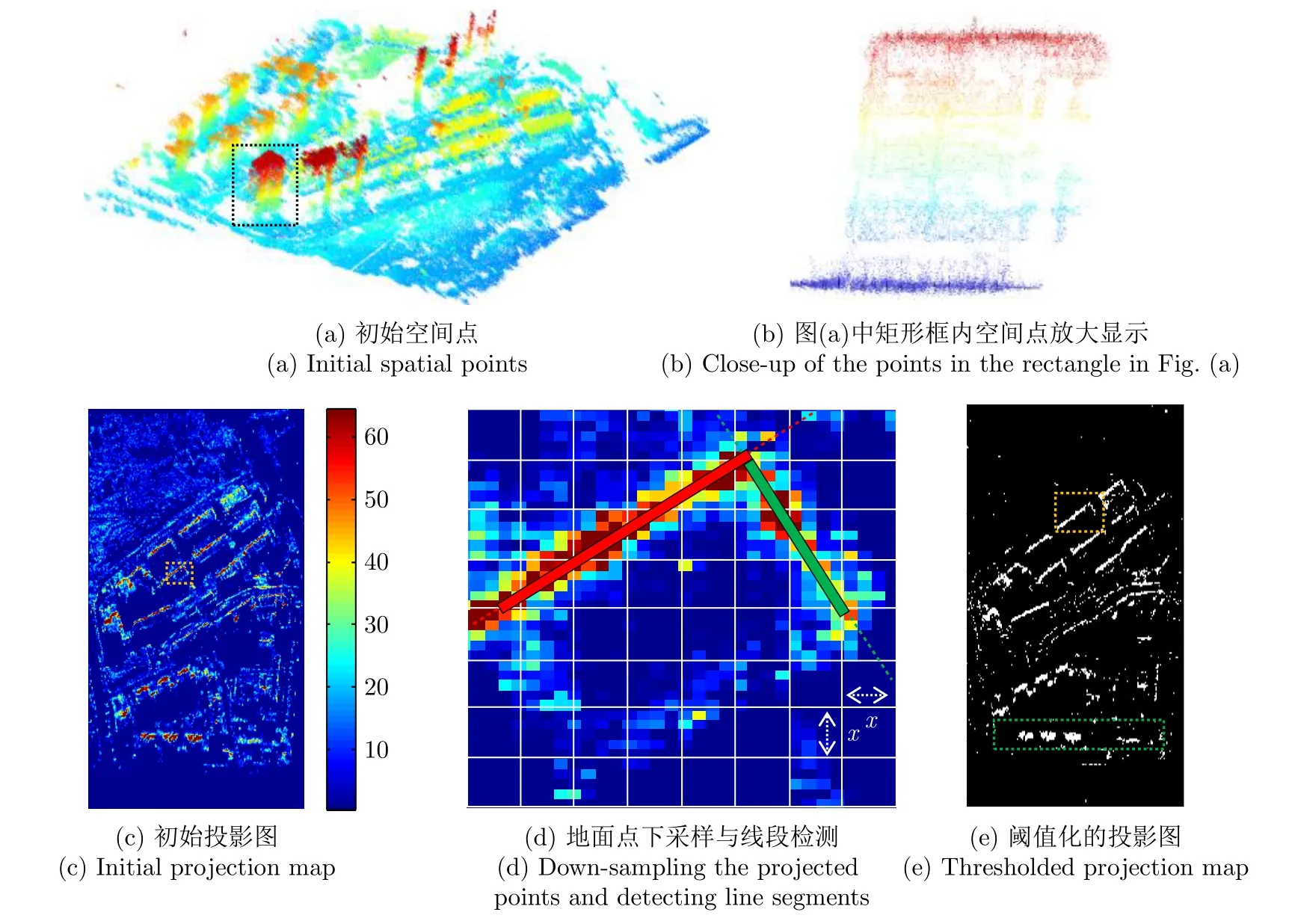
图2 投影图生成Fig.2 Projection map generation

根据以上分析，如图2(d)所示，通过在聚集的地面点中检测线段(矩形)，则可确定与建筑立面相对应的直线(虚线)，进而可根据直线的垂线与投影至线段上的空间点确定相应的建筑立面(参见3.4节)。考虑到后续环节整体线段检测的效率，本文对每个地面点对应空间点的数量进行了统计并利用尺寸为x×x的单元格对地面点进行分组(即下采样)，进而通过将每个单元格内地面点对应空间点数的最大值作为该单元格的“像素值”而生成一幅由单元格为基本构成单元(下文简称“像素”)的投影图。在实验中发现，尺寸较大的单元格有助于连接相近的地面点(或抵制噪声点对应的地面点)并提高线段检测的效率，但却不利于突出线段的结构以提高线段检测的精度(如采用尺寸为2 × 2单元格的效率比尺寸为1 × 1的单元格的效率要高4倍左右，但所检测线段的精度要低3%)。此外，为进一步降低噪声点或非建筑立面对应地面点对后续环节线段检测的影响，本文通过调整可变阈值(下文简称投影阈值)的方式(每次降低为当前值的一半)更新投影图中像素的数量；如图2(e)所示，将投影阈值的初值设置为所有像素对应“像素值”平均值的两倍后，“像素值”较小的像素被滤除，而“像素值”较大的像素则聚集而成相互独立且具明显线段结构特征的连通区域；事实上，此类连通区域包含的线段通常与主要建筑立面相对应且易于被检测，以此可构造特定的约束条件以实现潜在建筑立面对应线段的检测；另一方面，“像素值”较小的像素虽暂时被滤除，但当投影阈值降低而将其呈现后，由此生成的连通区域仍可能包含潜在的线段，因而也需要在已检测线段的基础上对此类线段进行检测。

3.2 主线段检测

在图2(e)所示阈值化的投影图中，连通区域通常具有以下特征：(1)单个连通区域包含1～2个线段且多个线段之间具有特定的夹角(如黄色虚线框内区域)；(2)相邻连通区域以较大概率位于同一直线上或具有特定夹角的多个直线上(如绿色虚线框内区域)。因此，本文首先在每个连通区域内检测具有明显线段结构特征的主线段，然后以此为基础进一步检测潜在的线段。

由于主线段结构特征较为明显，如图3(a)所示，采用常规的线段检测算法(如Hough变换[24]或LSD算法[25])即可获得较好的效果。然而，如图3(b)所示，由于噪声点的影响，连通区域内的像素往往并不完全位于同一直线，进而易导致在同一连通区域内检测到多个相近线段的冗余问题；此外，不同连通区域内检测到的线段也存在其所在直线(如斜率与截距相近)冗余问题。为解决此问题，本文首先定义以下标准度量线段相对连通区域的可靠性：

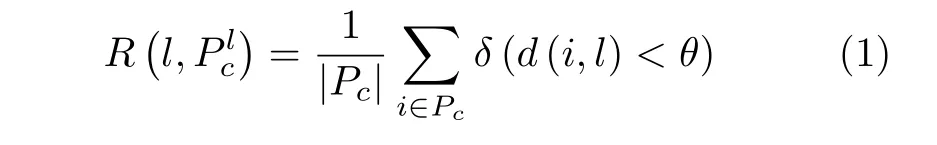
其中，l与c分别表示当前线段(或直线)与连通区域，Pc与|Pc|分 别表示连通区域c内像素集与像素总数，d(i,l)表 示像素i到线段l所在直线的距离，θ为距离阈值(设置为1)，表示满足d(i,l)＜θ条件的像素集合，δ(·)函数当条件为真时取值为1，否则取值为0。

在式(1)的基础上，本文采用以下步骤对冗余线段或直线进行剔除：

(1) 连通区域内冗余线段的剔除：对于在同一连通区域检测到的多条线段，首先在每个线段上通过均匀采样的方式生成点集，然后利用Hausdorff距离[26]度量两两线段对应点集之间的距离；若该距离小于指定阈值(设置为5)，如图3(c)所示，则将当前两线段视为相近线段并从中选择最小者作为冗余线段剔除。

(2) 连通区域间冗余直线剔除：对于每个连通区域内剔除冗余线段后保留的线段，首先将所在直线具有相近斜率的线段划分为同一组(不同组对应倾角之间的最小差异设置为10°)并求取该组内所有线段所在直线斜率的平均值，然后根据该斜率平均值与该组内所有线段的质心确定相应的平行直线；而对于多条通过多个相同连通区域的平行直线，本文通过以下标准从中选择最优直线而将其他直线作为冗余直线剔除：

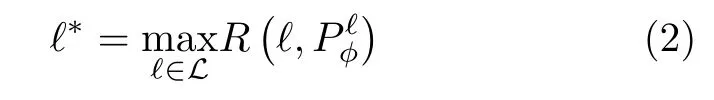
其中，φ为连通区域集中元素的并集(即)，L与ℓ*分别为平面直线集与最优直线。

图3(d)所示为最终确定的最优直线，从中不难发现，其在空间结构上基本与主要建筑立面相对应，因而有利于约束或引导后续环节的潜在线段检测过程以产生可靠的结果。为此，如图4(a)所示，本文进一步将其在连通区域内的部分作为该连通区域内检测到的线段并替换质心在其上的原线段，进而实现整体主线段的规则化。

图3 主线段检测Fig.3 Main line segment detection

3.3 潜在线段检测

在图4(a)所示规则化线段的基础上，本文进一步在连通区域内与连通区域之间检测潜在的线段。

3.3.1 连通区域内潜在线段检测

根据建筑立面之间具有特定夹角的结构先验[9]，本文将连通区域内潜在线段检测限定于与主线段具有特定夹角的方向上进行，进而提高整体线段检测的效率与可靠性。为此，如图4(b)所示(红色表示主线段，黄色与绿色分别表示潜在线段所有检测方向与最优检测方向)，本文通过建筑立面之间常见夹 角(即A=[0°,30°,45°,60°,90°,120°,145°,150°])设定潜在线段检测方向并利用以下标准从中确定最优潜在线段：

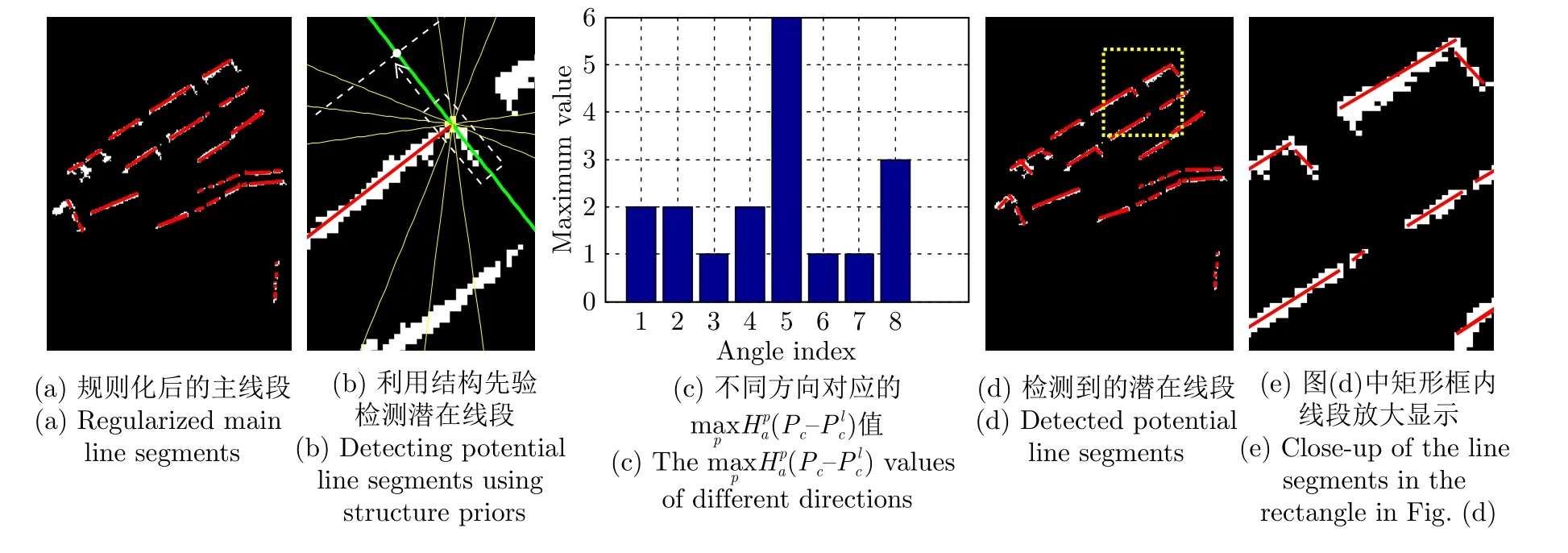
图4 连通区域内潜在线段检测Fig.4 Potential line segment detection in connected regions

3.3.2 连通区域间潜在线段检测

在已检测线段(包括主线段与潜在线段)及相应连通区域(设为M)的基础上，本文进一步在未检测线段的连通区域(设为)内检测潜在的线段。由于集合中的连通区域不具有明显的线段结构特征，因而需要根据已检测线段所在直线为其分配最优直线，进而确定其相应的线段；为此，本文利用连通区域间冗余线段剔除方法(参见3.2节)对集合M内连通区域对应的已检测线段进行分组以生成直线集L，进而定义以下标准为集合M¯中的连通区域分配最优直线：

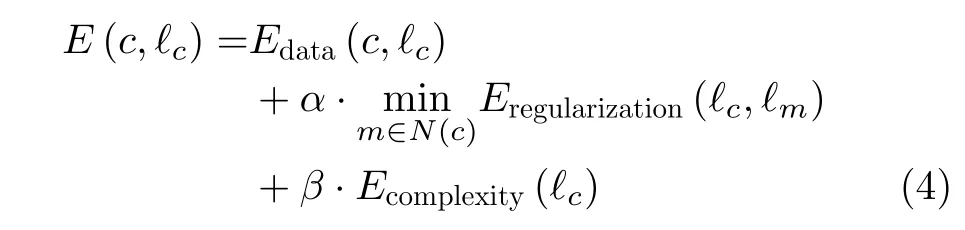
其中，ℓc表示当前为连通区域c∈分配的直线，N(c)表 示与连通区域c相邻的集合M中的连通区域，Edata(·),Eregularization(·)与Ecomplexity(·)分别表示数据项、规则化项与复杂度项，α与β分别为相应的权重(分别设置为0.7与0.3)。

(1) 数据项

数据项用于度量为连通区域c分配直线ℓc的代价，其定义为

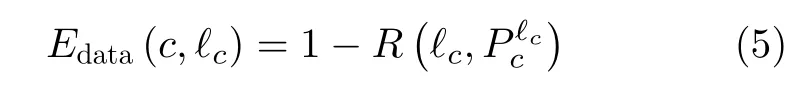
(2) 规则化项

规则化项用于增强相邻连通区域内的线段所在直线之间具有特定夹角的特征，其定义为

其中，D(c,m)表 示相邻连通区域c与m内像素之间的最小距离，〈ℓc,ℓm〉为 线段lc与lm之间的夹角，参数σ用于控制直线ℓc不满足规则化条件的惩罚强度(设置为10)。

(3) 复杂度项

复杂度项用于生成以最少直线拟合全部连通区域的精简结构，其定义为

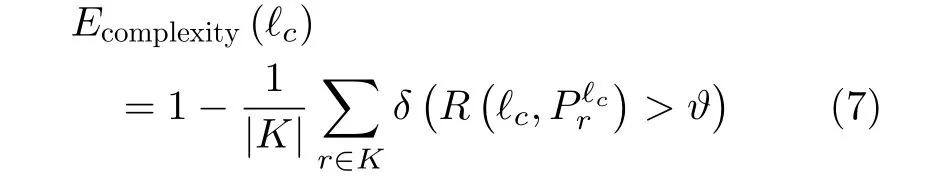
其中，K与|K|分别为所有连通区域集合与相应的总数，阈值ϑ控制复杂度惩罚强度(设置为0.9)。

在式(4)的基础上，如图5(a)所示(黄色方形与红色圆形分别表示当前连通区域及其相邻连通区域，灰色表示已检测线段的连通区域)，对于当前连通区域c∈，本文根据连通区域的质心并利用Delaunay三角化方法确定与其相邻的连通区域，进而为其分配最小E(c,ℓc)值对应的最优直线（或最优直线在连通区域内部的线段）。在此过程中，对于计算E(c,ℓc)值时的候选直线集，本文根据集合N(c)内连通区域相应线段所在直线与结构先验生成，进而缩小最优直线的搜索空间而提高整体效率与可靠性。

图5 连通区域间潜在线段检测Fig.5 Potential line segment detection between connected regions

此外，为提高连通区域相应直线推断的整体可靠性，本文定义以下连通区域对应直线推断优先级：

其中，|N(c)|表 示与连通区域c相邻的集合M内连通区域的数量，R(c)表 示包含连通区域c的最小矩形的最长边与最短边之比。

式(8)表示，若连通区域c∈具有明显的线段结构且可通过较多已检测线段构建其潜在线段检测空间，则应优先为其推断相应的直线，进而可提高集合中其他连通区域对应潜在线段检测的可靠性。

总体上，连通区域间潜在线段检测过程如算法1所示。

根据PBFD算法步骤，当降低投影阈值而更新投影图后，如图5(d)所示(绿色表示投影图更新后在新生成连通区域内检测的线段)，采用算法1仍可从新产生的连通区域中检测出一定数量的潜在线段。需要注意的是，在不同阈值化投影图及同一阈值化投影图的不同阶段中所检测的潜在线段之间可能存在冗余，因而需要进一步采用连通区域间冗余线段剔除方法(参见3.2节)对最终检测的潜在线段进行规则化处理；如图6(a)所示(不同斜率的直线用不同颜色表示，与直线相同颜色的圆形表示直线上线段质心)，此过程生成的直线较可靠地确定了建筑立面所在位置。在此实验中，本文也尝试采用文献[8]提出的CONSAC多模型(即直线)拟合算法对阈值化投影图中的直线进行了检测，如图6(b)所示(与直线具有相同颜色的点表示相应直线的内点)，由于较多像素未沿直线分布及噪声的影响，其结果并不理想(如所检测直线与真实直线存在偏差、检测直线较少等)。

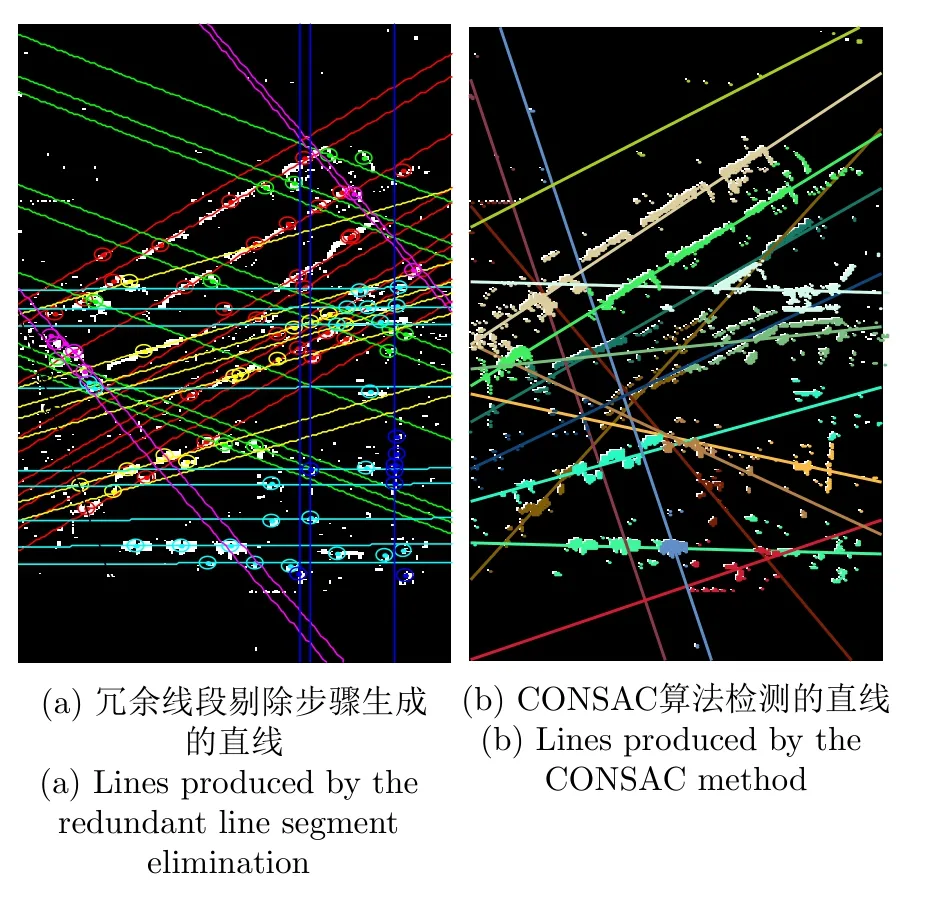
图6 不同算法检测的直线Fig.6 Lines produced by different methods

3.4 建筑立面生成

由于在投影图中检测的线段与建筑立面相对应，因而建筑立面可通过对应线段的垂线(即建筑立面法向量)及任意一个投影至该线段上的空间点确定。如图7(a)，图7(b)所示，在投影图中检测到的线段l1与l2所 在直线分别为ℓ1与ℓ2，而直线ℓ1与ℓ2的垂线则确定了其对应建筑立面H1与H2的 法向量n1与n2；因而，建筑立面H1与H2可 分别根据其法向量n1与n2以及投影至线段l1与l2上 的空间点p1与p2直接确定，从而避免了传统耗时的平面拟合过程。需要注意的是，图7(b)的红色与绿色矩形分别为投影至线段l1与l2上的空间点在建筑立面H1与H2上最大矩形包围区域。

为增强最终生成的建筑立面的可视化效果，本文将投影至线段上的空间点及其在对应建筑立面上区域进行了叠加显示；如图8(a)，图8(b)所示，两者在空间结构上较为一致，表明最终生成的建筑立面具有较高的可靠性；此外，由于此过程避免了较为耗时的平面拟合，因而也具有较高的效率。图8(c)，图8(d)所示为最终生成的建筑立面在两个不同视点下的效果，可以看出，其在整体上表达了建筑立面的基本结构与相互之间的关系，对后期初始空间点的规则化处理或建筑建模具有较好的辅助作用。

图8 最终生成的建筑立面Fig.8 Final generated facades

4 实验结果分析

为验证PBFD算法的可行性与有效性，除前文描述的“峨眉”数据之外，本文进一步采用“运城”数据[27]进行实验与分析。两个数据相应的点云由中国科学院空天信息创新研究院研制的阵列In-SAR三维成像系统[3]采集(“峨眉”与“运城”数据对应的通道数分别为12与8、带宽分别为810 MHz与500 MHz)的SAR数据通过幅相误差补偿、基于邻域约束的稀疏重建[1]等步骤生成；整体上，点云规模较大且存在部分建筑结构对应空间点缺失、噪声等问题；在建筑基本结构上，如图9所示，两数据相应建筑的相邻立面多以特定角度(如90°)相交，具有一定的规则性。

图9 光学图像示例Fig.9 Examples of optical images

本文实验环境为64位Windows 7操作系统(Intel 4.0 GHz 4核处理器与32GB内存)，算法采用Matlab语言实现。

4.1 参数设置

在“峨眉”与“运城”数据的实验中，PBFD算法采用相同的参数设置，具体设置方式如下：

在投影图生成(参见3.1节)中，在初始投影图的基础上，通过降低投影阈值可生成不同的投影图以探测其中的潜在线段，本文将投影阈值逐次降低为当前值的0.4至0.7倍数时，所生成的投影图偏差不大，因而将其设置为0.5；此外，不同单元格的尺寸对应的线段检测效率与精度不同(单元格尺寸越大，线段检测效率越高而精度却相对越低)，在本文实验中，统一采用2 × 2尺寸的单元格。

在主线段检测中(参见3.2节)，距离阈值θ设置较小易产生较少的主线段，而设置过大则可能产生较多的不可靠主线段；与此类似，两线段对应点集之间的距离阈值与不同线段组之间的倾角阈值设置过小或过大均可能导致部分冗余线段剔除失败、合并较多相近线段而不易检测潜在线段等问题。为此，本文综合考虑了主线段的可靠性、点云噪声水平与单元格尺寸等多个因素的影响，将其分别设置为1,5与10°(如在主线段较可靠而噪声水平较高且单元格尺寸较大时可采用偏大的阈值，否则采用偏小的阈值)时本文算法在两个数据集的实验中均获得了较好的效果。

在潜在线段检测中(参见3.3节)，本文算法通过融合结构先验与整体线段复杂度的方式推断小尺寸连通区域对应的直线。为确定相应的权重α与β，本文首先根据相邻连通区域之间的距离、连通区域与其可能所在直线之间的距离等值确定参数σ与阈值ϑ；具体而言，参数σ以所有相邻连通区域最小距离的最大值作为参考值而设置以控制直线不满足规则化条件的惩罚强度；此外，阈值ϑ越大表示连通区域位于当前直线上的像素越多，若此类连通区域较大，则表明当前直线较可靠，因而应给予较小的惩罚量。综合考虑，本文将参数σ与阈值ϑ分别设置为10与0.9；在此基础上，本文进一步以0.1的步长遍历区间[ 0,1]内 每个值并赋予权重α，然后在权重α的每个取值时采用同样的遍历方式调整权重β并输出最高的精确度(参见4.2节)，具体结果如图10所示。

从图10可以发现，权重α与β在分别取(0.6,0.7)与(0.3,0.4)时精确度基本偏差不大。事实上，较大的权重趋向于强制为相邻的连通区域分配相同的直线，而较小的权重则易导致不可靠的直线，本文最终将其分别设置为0.7与0.3。

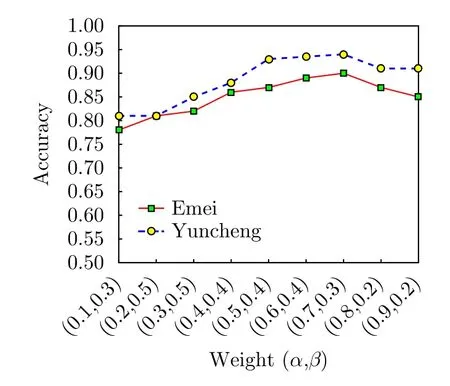
图10 不同权重对应的精度Fig.10 Accuracies corresponding to different weights

4.2 评估标准

为定量评价PBFD算法的性能，本文将初始空间点全部投影至地面后手工标注了建筑立面对应的直线(设为L)并以此作为真值；对于在投影图中检测到的线段l，则利用以下标准度量其可靠性：

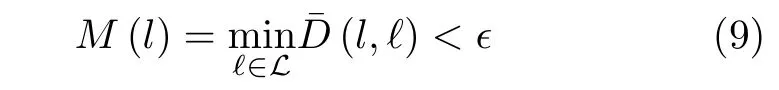
相应地，对于在投影图中检测到的直线，本文将其在投影图中的部分视为线段后利用式(9)度量其可靠性；在此基础上，利用“线段数-分组数-直线数”(N-G-L：检测出的线段总数-不同直线上的线段分组总数-检测出的直线总数)、精确度(P：推断的直线中正确直线所占比例)、召回率(R：推断正确的直线与所有真实直线的比例)与F1值(即精确度与召回率的调和平均值)评价在投影图中检测到的直线集的可靠性。

最终的实验数据基本信息如表1所示。

表1 数据基本信息Tab.1 Basic data information

4.3 结果分析

PBFD算法将三维空间的平面拟合问题转化为二维空间的线段检测问题进行求解，在由初始空间点生成的投影图中，通过结构先验的引导并采用渐近式的线段检测方式有利于提高整体效率与可靠性。对于如图11(a)所示的初始空间点，由于其相应地面点构成的连通区域具有明显的线段结构特征，如图11(b)，图11(c)所示，PBFD算法可有效检测其中的主线段。在此基础上，如图11(d)，图11(e)所示，利用已检测线段与结构先验构造当前线段的检测空间，则可在连通区域内与连通区域间检测出更多可靠的潜在线段。

图11 建筑立面检测Fig.11 Building facade detection

类似于“峨眉”数据，在此实验中，本文也采用CONSAC多模型拟合算法对阈值化投影图中的像素进行拟合以生成相应的直线，如图12所示，该算法检测出的直线不但与真实直线存在偏差，而且数量较少；相对而言，PBFD算法通过已检测直线与结构先验的约束，则获得了较多的可靠直线。

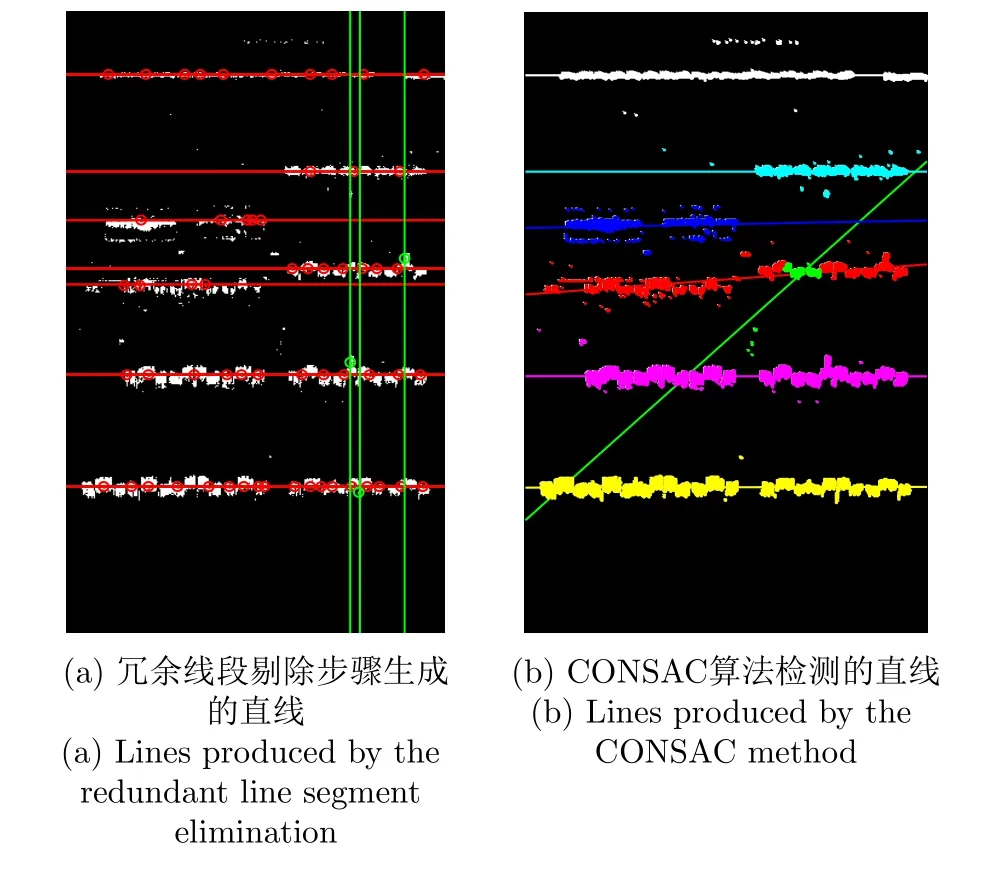
图12 不同算法检测的直线Fig.12 Lines produced by different methods

表2所示为PBFD算法的定量结果(Stage-I,Stage-II与Stage-III分别表示主线段检测、连通区域内与连通区域间线段检测、投影图更新后的线段检测)。从中可以看出，在Stage-I中，由于连通区域具有明显的线段结构特征，因而线段检测准确率较高；在Stage-II与Stage-III阶段，由于噪声点的影响，其线段检测准确率略有下降，但相应的召回率与F1值逐步增大，表明PBFD算法仍可检测出较多的可靠线段。相对而言，CONSAC算法虽可从投影图中检测出主要直线，但其在探测潜在线段时的性能较弱，因而相应的召回率与F1值较低。

此外，如表3所示(INI表示空间点投影与地面点下采样等预处理，LP表示由线段生成平面，灰色表示不同算法针对相同像素进行线段检测的时间)，相对于直接对空间点进行平面拟合，PBFD算法采用了计算复杂度更低的线段检测(即待确定的线段参数少且投影图中的像素也较少)方式实现平面的检测，同时利用已检测线段与结构先验对线段检测过程进行约束或引导，因而其整体效率也较高。

需要注意的是，针对INI阶段生成像素的直线检测，如表2和表3所示，PBFD算法在Stage-I与Stage-II两阶段的总耗时低于CONSAC算法的耗时而其精度却明显高于CONSAC算法的精度。此外，通过更新投影图，PBFD算法在Stage-III阶段可检测出更多直线且精度仍高于CONSAC算法。整体上，PBFD算法在3个阶段总耗时与CONSAC算法基本相当，但却可检测出更多的可靠直线。

表2 不同算法的精度Tab.2 Accuracies of different methods

表3 不同算法运行时间(秒)Tab.3 Running time of different methods (s)

根据以上实验分析，PBFD算法通过采用基于结构先验的线段渐近式检测方式实现平面的检测，可有效克服初始空间点数量及噪声的影响，整体上具有较高的性能。

5 结论与展望

针对从海量、带噪阵列InSAR点云中检测建筑立面的问题，本文将其转化为由空间点生成的投影图中的线段检测问题进行求解；其中，连通区域内与连通区域间的渐近式线段检测过程以及根据结构先验构造的线段检测约束空间有效保障了其整性效率与可靠性。实验表明，本文算法不但对空间点数量与噪声水平具有较好的适应性，而且所检测平面数量较多且可靠性较高。本文算法的不足及待改进之处在于：(1)仅对建筑立面进行检测而未考虑建筑顶平面；(2)未对缺失空间点的建筑区域对应平面进行推断；(3)过于稀疏的点云(初始投影图中具有明显线段结构特征的连通区域较少)可能导致所检测到的主线段较少而影响整体建筑立面检测的可靠性。针对此问题，可考虑采用将初始空间点投影至已检测建筑立面、全局平面优化、基于学习的点云稠密化等方法进行解决；在此基础上，通过融合更有效的结构先验(如长方体模型)、InSAR图像信息与基于学习的空间点特征将有望获得更好的效果。