若干层析SAR成像方法在解叠掩性能上的对比分析

任烨仙 徐 丰

(复旦大学电磁波信息科学教育部重点实验室 上海 200433)

1 引言

SAR具有全天候全天时成像能力，在遥感观测技术中不可或缺。受制于侧视成像的局限性，SAR影像不可避免地在高分辨率、复杂地物场景中出现大量收缩、遮挡和叠掩等几何畸变现象，上述现象严重影响了SAR影像的解译和判读。为此，在高程向再进行一次合成孔径的概念被提了出来。Knaell等人[1]将其称为雷达层析技术。雷达层析技术也可以视作对经典干涉SAR技术的推广，其最显著的特征在于可以分离叠掩散射体[2]，从而实现三维成像。

Reigber等人[3]最早开展了机载多基线层析技术的验证实验。Fornaro等人[4]推导了层析SAR成像方程，并使用TSVD方法在ERS数据上展开了成像实验。Budillon等人[5]使用压缩感知技术展开了TomoSAR成像仿真实验，并应用于ERS数据。早期的层析SAR数据分辨率不高，三维成像结果难以观察到清晰的结构信息。随着更高精度、更高分辨率的TerraSAR-X Spotlight数据的应用，获得更好效果的SAR三维成像结果变为现实。Zhu等人[6]提出了SL1MMER方法，该方法在L1范数最小化的结果上，使用贝叶斯信息准则(Bayesian Information Criterion,BIC)[7]去准确估计叠掩数，可以获得比以往算法更好的成像结果。Budillon等人[8]提出了检测叠掩的广义似然比假设检验(Generalized Likelihood Ratio Test,GLRT)方法，并以此实现三维成像，该方法成功应用于COSMO/SkyMed卫星数据的三维成像。Zhu等人[9]使用地理信息系统数据作为先验知识，结合组稀疏的方法进一步改进了观测数不足情况下的层析成像结果。此外，Ferro-Famil等人[10]和Tebaldini等人[11]针对植被等自然地物做了大量三维成像的研究工作。Nannini等人[12]采用极化层析的方法开展了林下目标成像与识别的研究工作。

在国内，柳祥乐[13]在InSAR的研究基础上，开展了层析合成孔径的早期探索研究。王金峰[14]和Wang等人[15]对层析SAR成像进行了仿真模拟。刘康[16]使用了层析技术在上海和武汉等城市的TerraSARX数据上进行了楼高的提取。Sun等人[17]使用Envisat-ASAR数据评估了压缩感知方法的层析聚焦性能。李震等人[18]综述了层析SAR在地表参数反演方面的研究进展。

最近，中国科学院空天信息创新研究院自主研发了机载阵列干涉SAR系统，并发布了运城和峨眉的阵列干涉SAR数据[19]。Jiao等人[20]提出了融合局部高斯-马尔可夫随机场的稀疏贝叶斯学习方法，对峨眉数据进行了层析成像，取得了非常好的实验结果。Zhang等人[21]提出了一种针对建筑墙角结构的层析成像方法，可以抑制墙角结构的散焦。李杭等人[22]提出了一种基于混合高斯分布模型的Tomo-SAR点云重建方法，有助于纹理贴图等后续操作。

本文以中科院空天院机载阵列干涉SAR的系统参数为基础，使用了克拉默-拉奥界[23,24]和重建成功率指标，系统性地比较了贪婪算法、迭代优化算法和超分辨率谱估计等层析谱估计方法，以及贝叶斯信息准则和广义似然比检测等叠掩模型定阶方法的性能，探索了叠掩散射体间的相互干扰作用(包括幅度比、相位差和散射间距)对层析解叠掩的影响。

本文其余部分的组织结构如下：第2节首先阐述了SAR层析成像的模型与克拉默-拉奥界精度分析工具。第3节和第4节分别介绍了几种最具技术潜力的层析谱估计和叠掩模型定阶方法。第5节以中科院空天院峨眉数据系统参数为基础，开展了分离叠掩散射体的仿真实验。此外，给出了一个实测场景的对照成像结果。第6节总结全文。

2 SAR层析成像的模型与精度

SAR采用斜距投影的成像几何在方位-距离平面上成像。高程向是垂直于该平面的第3个维度。当有多个地物目标与雷达天线的斜距相同时，会发生若干强散射体的“叠掩”现象。上述现象常常出现在城区、森林和陡峭地形的场景中。若共有M景经配准等预处理后的单视复数干涉影像，则其中第m景的任一像元g(ξm) 可以表示为后向散射信号在高程向s的积分[4]

其中，ξm=2bm/(λr) 表示空间(高程向)频率，bm表示基线长度，λ表示波长，r表示斜距，Δs表示散射体在高程向的分布范围，γ(s)表示后向散射系数在高程向的分布。式(1) 使用了一个简单的傅里叶变换，将观测量、系统参数(基线、波长、斜距)和后向散射系数分布有机地联系在一起，所描述的成像几何图像如图1所示。

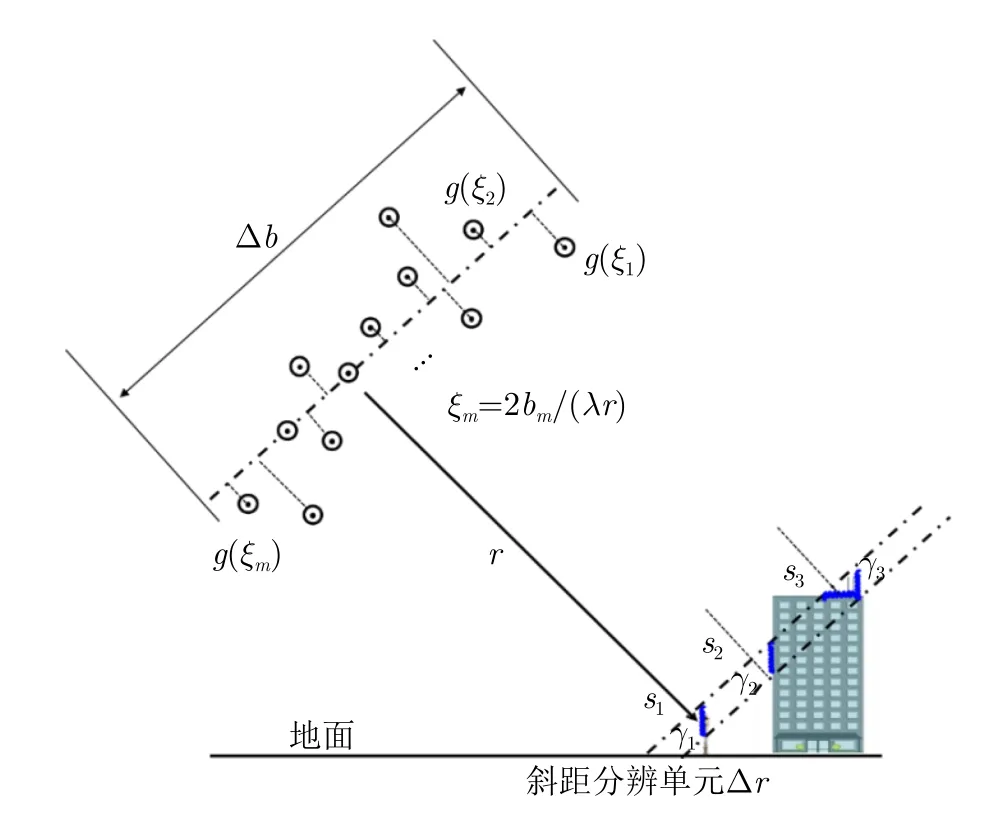
图1 层析成像几何示意图Fig.1 Imaging geometry of tomographic SAR

如果对高程向s进行L次网格化离散采样(sl,l=1,2,...,L)，则可以得到M个方程所构成的线性方程组

其中，g=[g1,g2,...,gm]T代表观测矢量，Aml=exp(j2πξmsl)代 表观测矩阵元素，γ=[γ1,γ2,...,γL]T是对高程向后向散射分布γ(s)的 离散化采样，ε是噪声矢量。由于L ≫M，所以式(2)是一个欠定方程组。

为了简化问题，噪声矢量ε一般假设为平稳的零均值高斯白噪声，这样可以得到观测矢量g的分布模型[23]

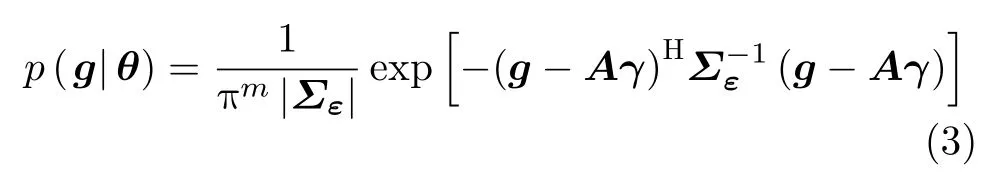
其中，Σε=σ2I表示噪声的协方差矩阵。该矩阵假设各个观测的噪声相互独立，且与强散射回波源无关。

上述高斯分布式 (3)的费希尔信息矩阵[23]是

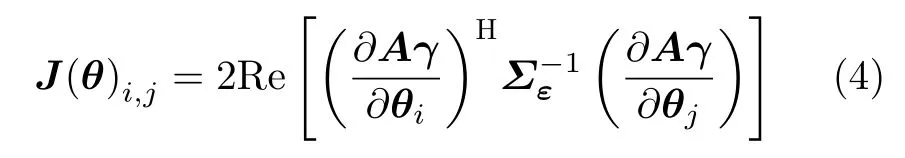
其中，θ代表模型中所涉及的参数，包括K个散射体对应的幅度ai，相位φi和高程si(i=1,2,...,K)。费希尔信息矩阵求逆，即获得克拉默-拉奥界CRLB=J-1。该界限反映了算法所能达到的极限估计精度。特别地，一个非混叠散射体的 CRLB矩阵是3阶矩阵，其中，C RLB(3,3)是高程估计s的克拉默-拉奥界[24]

其中，σ(s)表示高程估计的标准差，SNR表示信噪比，σ(b)表示基线的标准差。不等式(5)表明在给定系统参数的情况下，层析的高程估计精度与观测数和信噪比正相关，观测数累积越多，数据信噪比越高，高程估计越准。

当存在两个叠掩散射体时，等式(4)的费希尔信息矩阵是一个6阶的代数矩阵，其逆矩阵的代数形式变得非常复杂，难以写出对角线项的表达式。但结合系统参数与等式(4)，可以数值模拟费希尔矩阵，再对矩阵数值求逆，从而画出在给定信噪比时的高程估计精度的理论极限曲线图。

在层析三维成像中，相比于散射体的幅度和相位的估计精度，我们更加关注散射体高程估计的精度。这是由层析成像方程式(2)决定的。如果能够准确获得散射体的位置，在高斯白噪声下幅度和相位的最优估计，就是最小二乘法的结果

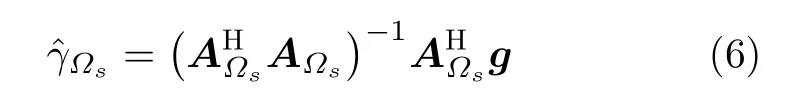
其中，Ωs代表散射体高程位置的支撑集合。式(6)表明在三维层析问题中，获得精确的叠掩模型AΩs具有最高优先级。

3 层析谱估计方法

在层析三维成像中，高程向的分辨率相较于方位向和距离向低了一个数量级。因此，在高程向聚焦使用超分辨率技术是必要的。考虑到叠掩数相对于高程采样数的稀疏性，欠定线性方程组式(2)的求解可以施加稀疏性约束(即L0范数最小化)

对于式(7)，可以直接使用贪婪算法，如正交匹配追踪(Orthogonal Matching Pursuit,OMP[25])进行求解，但需要给出确切的叠掩数K。在第4节会讨论如何估计叠掩数K。式(7)可以进一步写成岭回归的形式，L0范数可以近似为L1范数[26]

其中，λK是一个需要根据噪声程度调节的超参数。式(8)可以使用梯度类算法进行优化求解。在层析成像中，感知矩阵是狄拉克-傅里叶字典，其字典相干参数为，即观测数M越少，字典中原子间的相干性越强。在观测数M很少时，会导致式(8)的求解结果产生大量杂散点。Zhu等人[6]在求解出式(8)后的结果上使用BIC准则剔除杂散点，从而获得真实的叠掩数。Ma等人[27]通过迭代重加权最小L1范数的方法获得更稀疏的层析谱估计结果。Tan等人[28]提出了一种基于Lq(0＜q ≤1)范数的迭代稀疏学习(Sparse Learning via Iterative Minimization,SLIM)方法，证明了该方法与迭代重加权法等价，且计算量小很多。SLIM将式(8)的优化问题调整为

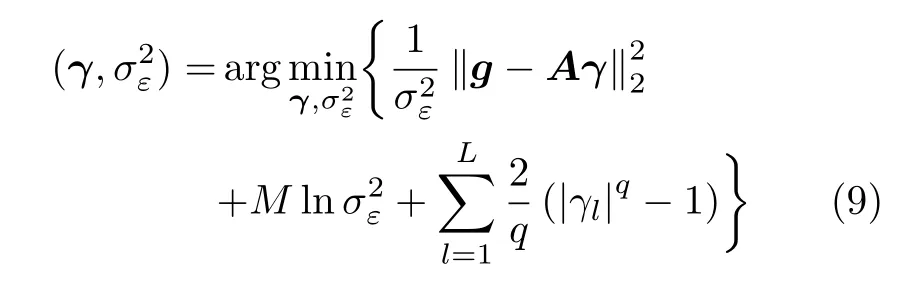
其中，q∈(0,1)是 一个需要调节的超参数，当q=1时，退化为最小化L1范数。式(9)可以通过共轭梯度最小二乘法进行求解。一般迭代20次左右收敛。多重信号分类算法[29](Multiple Signal Classification,MUSIC)是最经典的超分辨率谱估计算法。MUSIC算法将观测矢量的2阶统计量(即协方差矩阵)特征值分解为信号子空间与噪声子空间

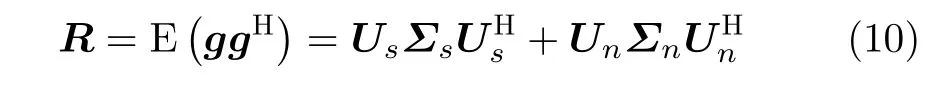
其中，E(·)表 示期望运算，R表示互相关矩阵。在本文中，互相关矩阵是对配准后的多通道层析影像上逐个像素开5×5的局部邻域窗口进行集合平均获得的。利用噪声子空间与观测矢量的正交性，可以获得

其中，a(sl)是感知矩阵A中的原子。

4 叠掩模型定阶方法

在涉及混合分布组分和模型阶数的估计中，基于信息论的贝叶斯信息准则[7]是最常用的估计方法

广义似然比检验[8]通过比较低、高阶模型的似然比和预设门限的大小，来探测成像模型拟合观测矢量所需的最优阶数(即叠掩数K)。该假设检验过程包含K步二元假设检验，其中，第i步(i=1,2,...,K) 假设检验是：Hi-1有i-1个散射体在一个像元。HK≥i至少有i个散射体在一个像元。该过程为

其中，Ti是第i步的假设检验阈值，是所选择的支撑集的组合子集Ωi。该假设检验过程遵循奥卡姆剃刀原理：相近逼真度下，越简单的模型是越好的模型。换而言之，如果较小的叠掩数已经满足拟合的误差要求，就没必要假设更多的叠掩数。

需要特别指出的是，第3节提到的SLIM方法与MUSIC方法自带了对叠掩模型阶数的估计。在SLIM方法中，层析谱的锐化程度由噪声功率和超参数q共同控制，噪声功率会在迭代中不断优化更新。因此，不需要借助模型定阶，就能产生十分稀疏的层析谱；MUSIC方法则通过协方差矩阵的特征值分解直接划分信号子空间和噪声子空间，其中，信号子空间的维数就是散射体的叠掩数。在第5节的MUSIC方法的实验中，假定信号子空间的特征值之和占到总能量的85%以上，并以此作为阈值来确定叠掩数。

5 实验与评估

以中科院空天院峨眉机载数据为例，其入射角从近距端21°变化到远距端47°。本文选取峨眉数据入射角较大时所对应的参数来进行计算(如表1所示)，可以画出两个虚拟的散射体在不同叠掩距离下高程估计精度的克拉默-拉奥界图(如图2所示)。

图2 峨眉数据的克拉默-拉奥界Fig.2 The Cramér-Rao Lower Bound (CRLB) of the Emei data

为了方便起见，本节实验只针对两个散射体(即 (a1,φ1,s1) 和(a2,φ2,s2),K=2)发生叠掩的情形。如果具体化层析成像方程式(1)，可以得到

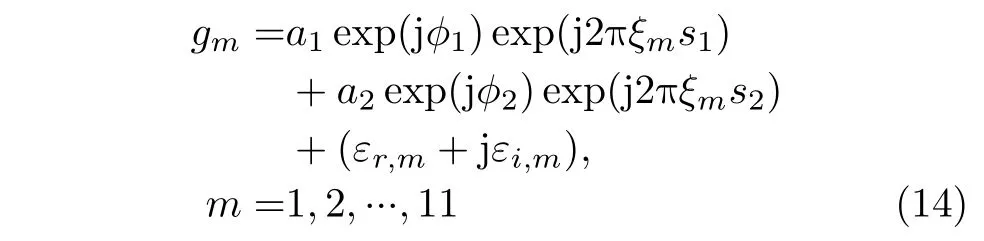
其中，ξm通过表1的参数确定，εr,m+jεi,m代表圆对称零均值高斯随机噪声。对于永久散射体来说，其信噪比一般介于3～10 dB。在本节实验中，信噪比统一设置为5 dB。

表1 峨眉数据的参数Tab.1 Parameters of Emei data

为了评估第3、第4节所提到的算法的高程估计精度能否达到克拉默-拉奥界，本文首先假设了叠掩的散射体a1exp(jφ1)和a2exp(jφ2)是独立且均匀随机的，即幅度和相位均服从均匀分布a～U(0,1),φ～U(0,1)。需要注意的是，如果不对散射体的幅度和相位做出上述均匀假设，就没有办法获得预期的结果，使得高程估计的标准差与克拉默-拉奥理论界限可以进行相互比较。这是因为克拉默-拉奥界本质上是估计量方差的理论极限，比较方差大小的前提是本身均值不能偏太多。但事实上，除了高斯噪声引起的估计量的方差波动之外，两个散射体的幅度比a1/a2和 相位差Δφ=φ1-φ2会影响许多谱估计算法的统计无偏性，最终导致估计高程的数学期望发生偏移。在期望发生偏移的情形下，比较方差是没有意义的。本文会在后面的实验中讨论估计量期望偏移这一现象。

通过蒙特卡罗仿真可以获得大量指定高程位置s1和s2的随机叠掩散射体。利用第3、4节中方法可以反演出这些叠掩散射体的高程分布。不失一般性，采用二元混合高斯分布建模：

其中，πk表示分布混合权重，μk(s)表示成像算法估计的第k个散射体高程的均值，σk(s)表示对应的标准差。图3展示了使用二元混合高斯分布拟合OMP算法估计高程位置分布的曲线。使用E-M算法[30]，可以计算出式(15)中的μ1(s)±σ1(s)和μ2(s)±σ2(s)。将它们与克拉默-拉奥界区间s1±CRLB(s1)和s2±CRLB(s2)进行比对，可以评估算法能否达到理论极限。

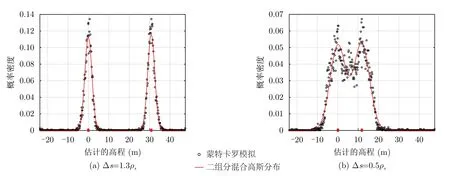
图3 由OMP算法估计散射体位置分布及其对应的高斯混合分布拟合曲线Fig.3 The probability density function of scattering position estimated by OMP and its corresponding Gaussian mixture distribution fitting curve

图4分别展示了OMP-BIC,OMP-GLRT,SLIM和 MUSIC等方法的高程估计精度。图4表明上述算法在该实验条件设置下，均能达到克拉默-拉奥界精度。其中，OMP分别采用了BIC和GLRT两种模型定阶方法估计叠掩数K。BIC和GLRT定阶的效果相差无几，GLRT具有恒虚警率特性，但BIC的计算会更加简单。在小于1/2的瑞利分辨率时，SLIM算法的超分辨率性能要优于OMP算法，但它的计算量也更大。尤其是对高程s进行密集采样时，SLIM算法会变得异常缓慢。在图4(d)中，MUSIC算法的估计性能明显优于其他算法，在信噪比为5 dB时的估计精度就达到了信噪比在23 dB情况下的CRLB，这是因为MUSIC算法处理的是平均后的2阶统计量。2阶统计量比原观测矢量的信噪比更高。上述实验结果表明，在对植被等自然随机媒质进行层析成像时，MUSIC算法会优于OMP,SLIM这类稀疏重建算法。

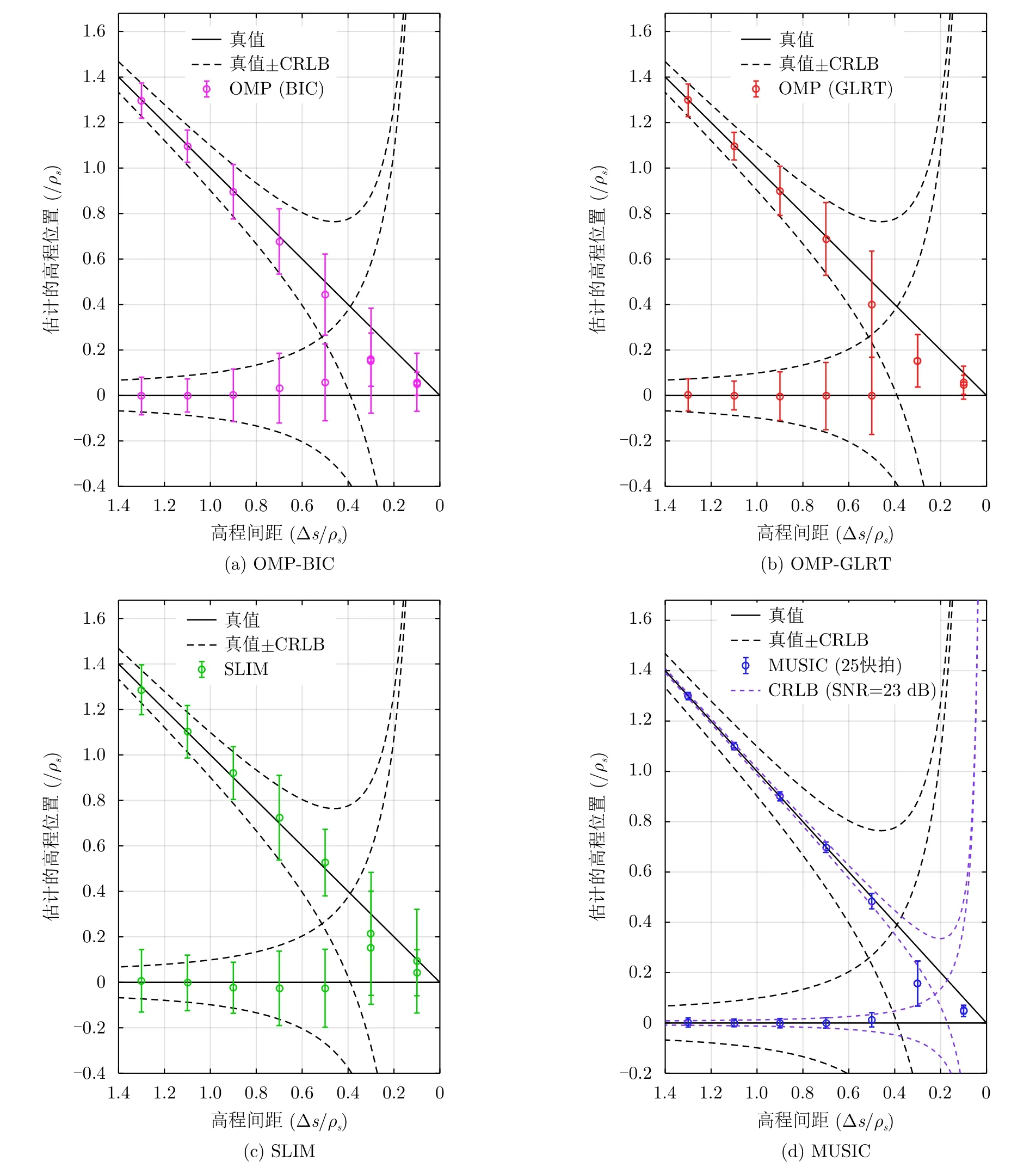
图4 不同算法的高程估计精度(M=11,SNR=5 dB,ρs=23.7805 m)Fig.4 Elevation estimation accuracy of different algorithm (M=11,SNR=5 dB,ρs=23.7805 m)

为了研究不同性质的散射体发生叠掩，对层析成像算法分离叠掩散射体的具体影响，我们需要定义层析算法重建成功的标准(以两个散射体发生叠掩为例)：

其中，式(16)K=2是叠掩模型的阶数，如果算法估计的K大于2，表明出现了杂散点；如果算法估计的K小于2，表明出现了结构缺失；式(17)和式(18)是对散射体定位准确性的判定。在实验中，α固定为 1/8。同时，实验通过两万次蒙特卡罗模拟来获得重建成功概率。

本文使用幅度比a1/a2、相位差Δφ=φ1-φ2和叠掩间距 Δs=(s1-s2)/ρs来衡量两个叠掩散射体在幅度、相位和高程上的差异。图5—图8分别展示了幅度比、相位差和叠掩间距等性质差异对层析重建成功率的影响。

图5展示了幅度比与重建成功率的函数曲线。限制相位差为 Δφ=π/2,Δs/ρs=0.7。图5表明，当一个叠掩散射体相对于另一个散射体能量很小时，算法是无法解叠掩的。在4种方法中，OMP-BIC受幅度比的影响相对较小。同时，我们也观察到在限定叠掩散射体相位差、高程差的情况下，幅度比对MUSIC算法的影响很大。图9展示了当限定叠掩散射体幅度比a1/a2=0.5，相位差Δφ=π/2时，MUSIC算法在不同叠掩间距下估计高程的均值和标准差的图像。图9表明叠掩散射体中幅度相对较弱的散射体的定位完全偏离了真实位置s1。

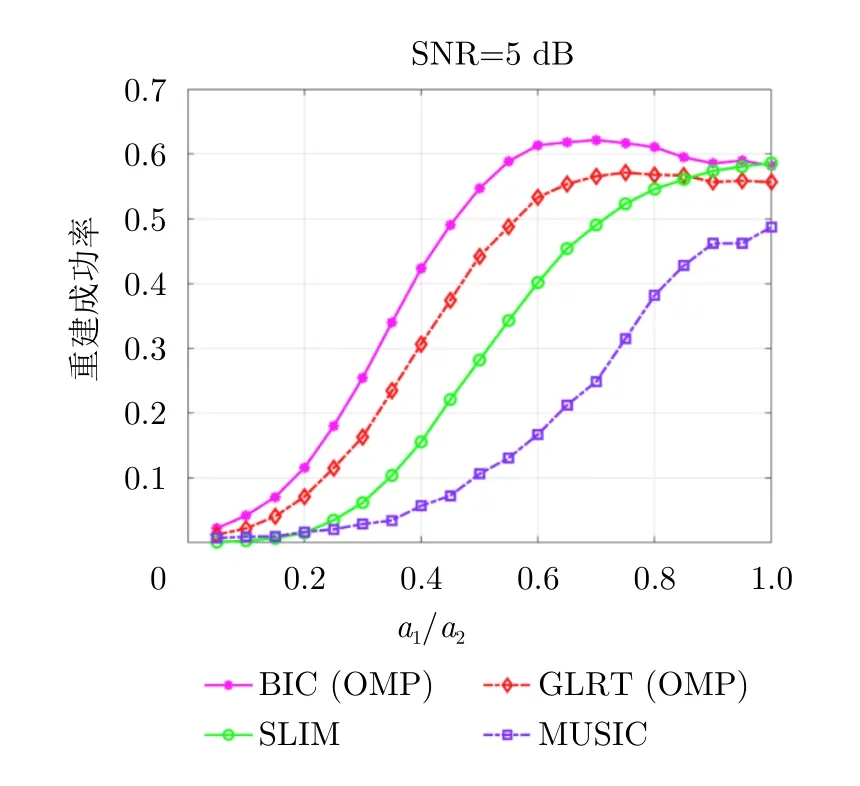
图5 OMP-BIC,OMP-GLRT,SLIM,MUSIC的重建成功率与叠掩散射体的幅度比a 1/a2的函数关系Fig.5 Recovery probability as a function of amplitude ratio a1/a2 obtained by using the OMP-BIC,OMP-GLRT,SLIM and MUSIC

图6 OMP-BIC,OMP-GLRT,SLIM,MUSIC的重建成功率与叠掩散射体的相位差 Δφ的函数关系Fig.6 Recovery probability as a function of phase difference Δφ obtained by using the OMP-BIC,OMP-GLRT,SLIM and MUSIC

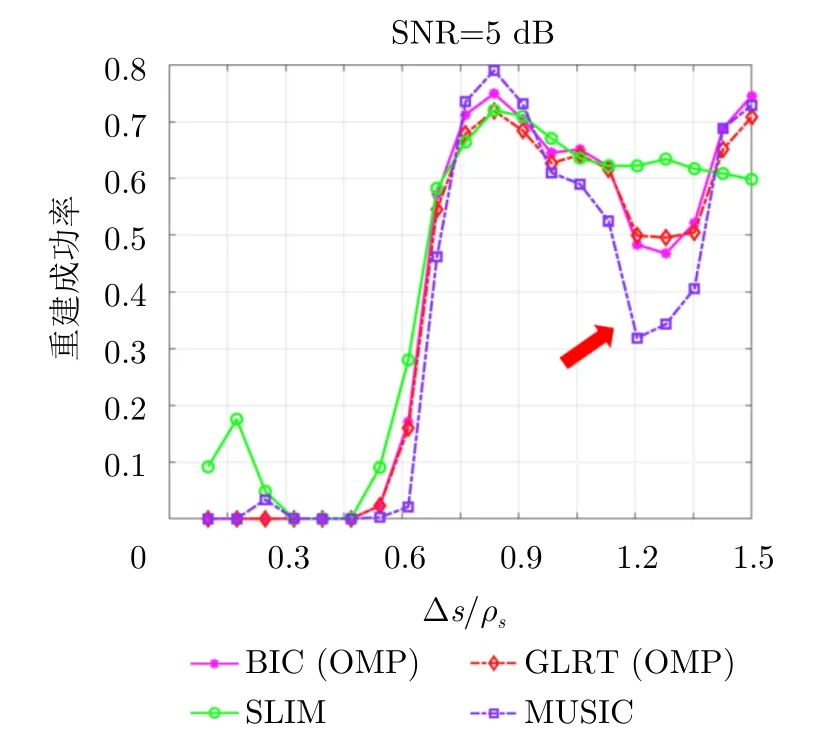
图7 OMP-BIC,OMP-GLRT,SLIM,MUSIC的重建成功率与叠掩散射体的规范化高程间距Δ s/ρs的函数关系Fig.7 Recovery probability as a function of elevation distance Δs/ρs obtained by using the OMP-BIC,OMP-GLRT,SLIM and MUSIC

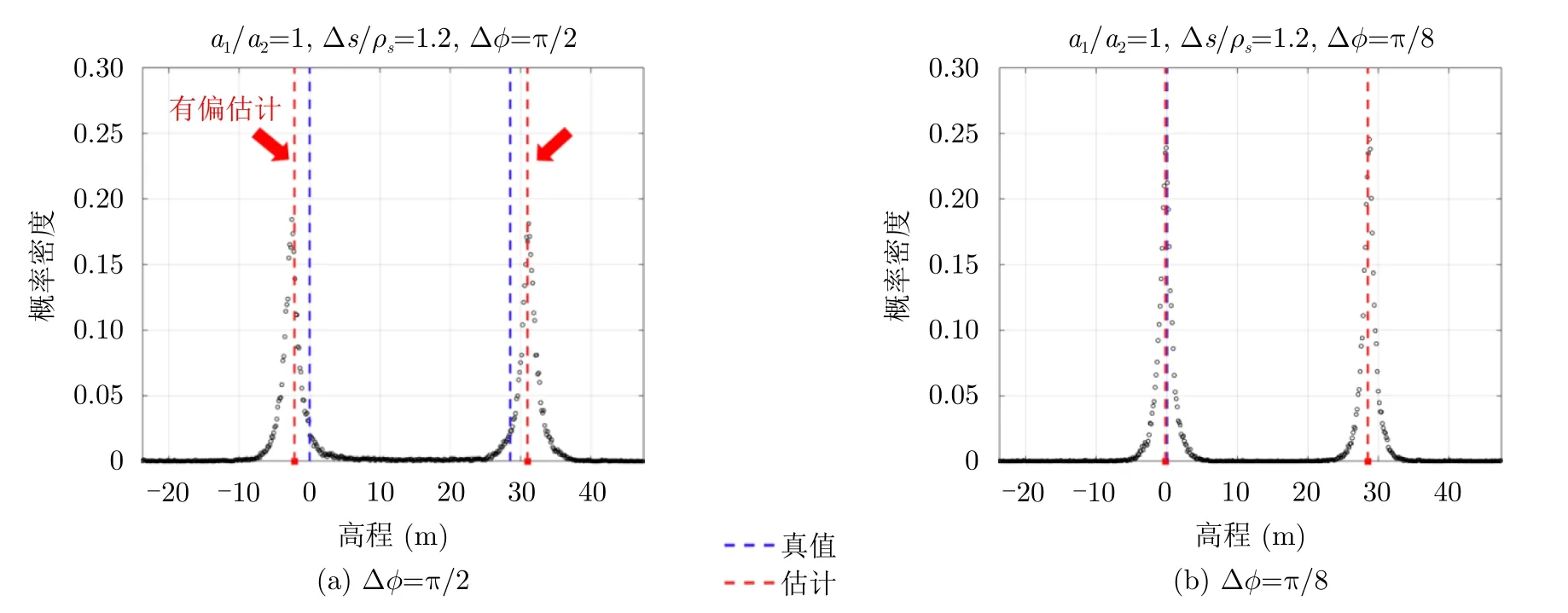
图8 叠掩散射体间的相位差对MUSIC算法谱估计结果造成的扰动效应(图 8是图 7中1 .2ρs附近发生重建成功率异常下降的解释)Fig.8 The disturbance of height estimation caused by phase difference Δ φ between overlapped scatterers(Fig.8 is an explanation of the abnormal decrease in the recovery rate in Fig.7)

图9 MUSIC算法的高程估计精度(当限定a 1/a2=0.5时，能量小的散射体位置估计出现明显偏差)Fig.9 Elevation estimation accuracy of MUSIC algorithm (When the amplitude ratio is fixed at 0.5,the position estimation of the scatterer with small energy is obviously deviated)

图6展示了相位差与重建成功率的函数曲线。限制幅度比为a1/a2=1,Δs/ρs=0.7。图6表明相位差 Δφ对重建成功率的影响呈现周期性变化。相位差对OMP-BIC/GLRT，MUSIC的影响很大，对SLIM算法影响相对较小。

图7展示了叠掩间距与重建成功率的函数曲线。限制幅度比为a1/a2=1，相位差为Δφ=π/2。从经验上讲，散射体的间距越大，应该越好解叠掩。但事实并非如此，图中的红色箭头标记了在叠掩间距1.2ρs～1.35ρs上重建成功率突然下降的异常状况。图8展示的统计分布表明，在叠掩间距 1.2ρs附近，MUSIC算法的重建成功率突然下降恰好是由相位差Δφ=π/2 的 干扰导致的，因为如果将相位差Δφ改为π /8，则图8(a)的有偏估计就会变成图8(b)的无偏估计。这意味着叠掩散射体间的相位差极易对某个小区间的高程线性相位产生扰动效应，使得该区间处高程估计量从无偏估计变为有偏估计。

图10(a)是从谷歌地球截取的光学图像块。图10(b)是从中科院空天院峨眉数据截取的 900×740图像块。图10(b)的红色箭头1标记了高楼屋顶和墙面的散射体叠掩，箭头2标记了高楼墙面与低矮建筑屋顶的散射体叠掩，箭头3标记了墙角处的散射体叠掩。其中，箭头1和箭头3标记的叠掩处于瑞利分辨率内，箭头2则处于瑞利分辨率外。

图11(a)—图11(d)分别是与图10(a)中红虚线对应的OMP-BIC,OMP-GLRT,SLIM和MUSIC层析结果的距离-高程切片。该反演结果没有进行地斜距坐标系转换。图12完整地展示了经过坐标系转换后的OMP-BIC,OMP-GLRT,SLIM和MUSIC层析成像结果。

图10 峨眉数据的场景(红色的箭头标记了切面上的三处叠掩)Fig.10 The scene of Emei data (The walls of tall buildings and the roofs of low buildings are overlapped)

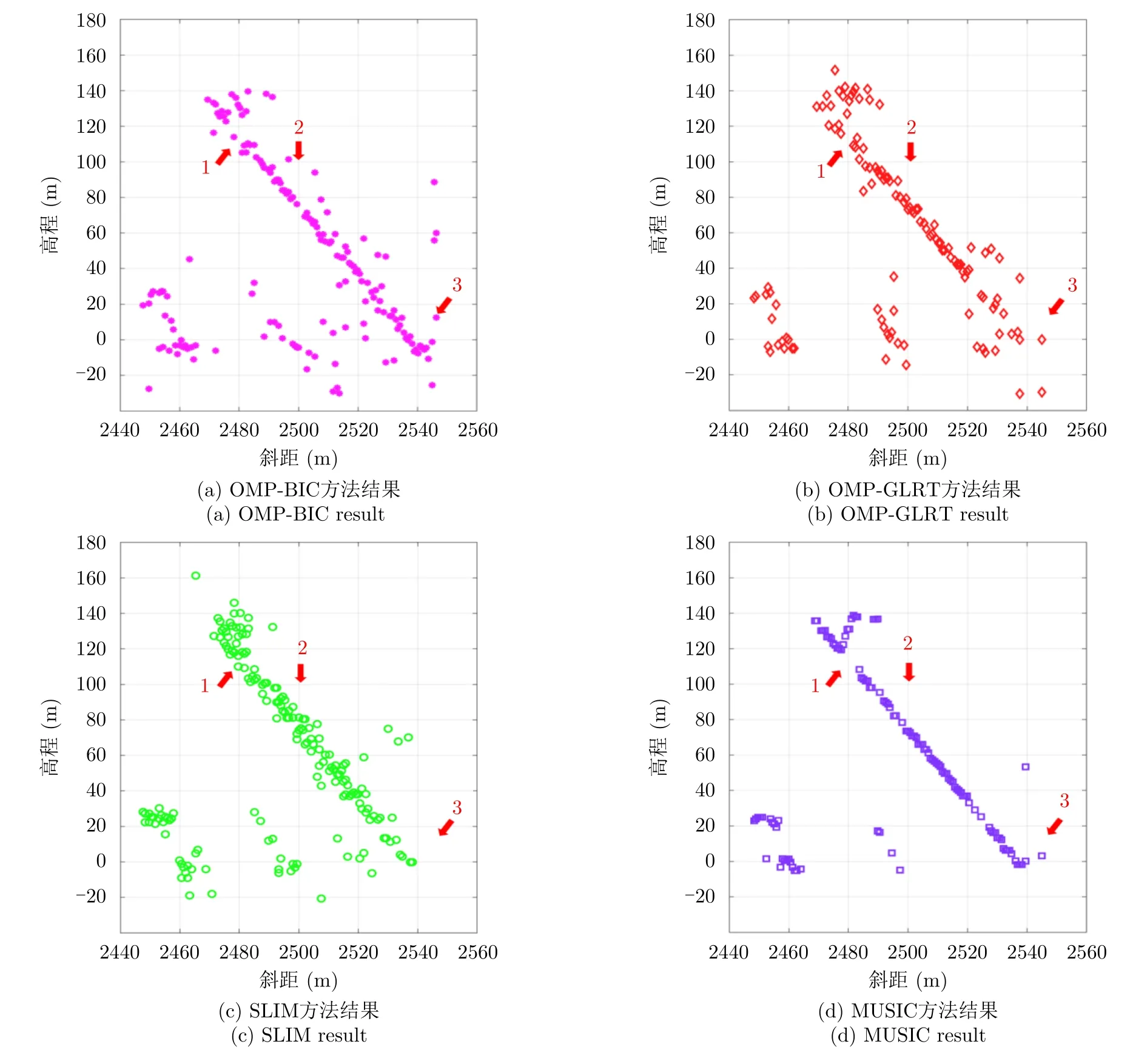
图11 与图 10中红虚线对应的距离-高程切面图(未经过地理编码)Fig.11 Range-Elevation section corresponding to the red dotted line in Fig.10 (without geocoding)

图12 层析成像结果(经过地理编码)Fig.12 Tomography results (after geocoding)

从聚焦效果上看，MUSIC方法对楼面的聚焦效果要优于其他3种方法，这是因为2阶统计量获得高程估计的方差比单个观测矢量更小；SLIM倾向于生成更密集的点云，但也产生了更多的杂散点；OMP-GLRT产生的杂散点数量略微少于OMPBIC，但GLRT在处理实测数据时往往需要多次调整门限参数，来改善成像结果，这导致了GLRT比BIC计算量更大。

从解叠掩效果上看，对于箭头1、箭头2标记的叠掩，OMP-BIC和OMP-GLRT表现的效果更好，但噪声和瑞利分辨率制约了成像结果的精细化。SLIM在杂波的干扰下，倾向于高估叠掩数。和前文的分析一样，当两个幅度差异较大的散射体叠掩时，MUSIC算法倾向于只定位较大幅值散射体的位置，而忽略掉较小幅值的散射体，这导致了图11(d)中MUSIC结果的1、2处墙面结构的缺失。对于箭头3标记的叠掩，OMP和SLIM方法的散焦很严重，这是因为建筑物墙角底部存在多路径导致的复杂散射机制，导致了观测矢量与线性相位模型的失配。图11(d)箭头3则表明，对于复杂散射机制，基于二阶统计量的MUSIC方法倾向于只获得其等效相位中心，因此实验观察到的散焦相对较小。

从理论上来讲，峨眉数据两个叠掩散射体的克拉默-拉奥界在约 0.5ρs(约11.5 m)处相交，这意味在不引入其他先验作为约束的情况下，对斜高小于11.5 m的结构进行超分辨率成像都是模糊的。而墙角与屋顶都存在斜高尺度上小于11.5 m的叠掩结构，因此，由克拉默-拉奥界制约的超分辨率性能是导致点云扩散的原因之一。可以观察到墙角层析的散焦往往会比屋顶的散焦更严重，这是阵列干涉SAR的固有缺陷导致的。由于采用单航迹多站接收的模式，阵列干涉SAR与传统的多航迹单站接收模式的层析SAR不同，它会将偶次反射回波信号识别为低于地面和高于地面的两个单次反射回波[31]，这是阵列干涉SAR墙角附近严重散焦的重要原因。

6 结论

本文采用了峨眉数据远距端的参数，进行了蒙特卡罗模拟实验；使用了多种超分辨率算法和模型定阶方法进行了分离叠掩散射体的层析反演实验。实验表明对于幅度和相位均匀分布的叠掩散射体，使用2阶统计量获得高程估计的方差比单个观测矢量更小。叠掩散射体幅度比，相位差和叠掩间距都会对算法解叠掩效果产生影响。一般认为，高程估计量的系统性偏移都是由定标残留的相位误差导致的，但是，本次实验发现叠掩散射体间的相位差Δφ本身就会对特定高程处线性相位的匹配产生负面作用，使得高程估计量从无偏估计变为有偏估计。迭代类优化算法能在一定程度缓解上述问题。