基于智能算法和数值模拟协同的凸轮轴锻造优化*
2022-03-05洪小英李亮亮
洪小英,李亮亮,王 乐
(1. 四川信息职业技术学院,四川 成都 628017;2. 重庆大学 材料科学与工程学院,重庆 400044)
0 引言
锻造成型工艺参数优化,一直是制造工业中的核心内容之一。合理的锻造工艺不仅能够节材、提高成型质量,还能够降低成型载荷。对于锻造成型工艺参数的优化,目前普遍使用的方法还是试错法。近年来一些有效的方法被提出。汤禹成等[1]用人工神经网络构建设计变量与设计指标之间的映射关系,并用粒子群算法对映射关系进行了寻优;其寻优结果表明,这种策略能够解决预锻模的优化设计问题。吴彦骏等[2]使用克里金模型、神经网络构建预锻模具形状与成型载荷、成型质量之间的响应关系,并用遗传算法对响应进行寻优;其方法显著提升了成型质量、成型载荷下降了40%。刘洪玉等[3]用直接搜索算法、粒子群算法、遗传算法3种算法对多工位锻造过程进行了多目标优化,其研究结果表明,遗传算法的优化效果最为显著,载荷下降了26.6%,填充得到显著改善。张子伟等[4]用曲线拟合方法拟合出模具形状和填充率之间的关系,并对拟合方程进行最优求解,获得了最佳模具参数。张明月等[5]使用BP(Black Propagation)神经网络和多目标遗传算法相结合的方法对齿轮坯预锻件进行多目标优化,并得到终锻成型力最小,且终锻模具最大应力最小时的最佳的预锻件形状和尺寸。除了代理模型和优化算法相结合的优化策略外,基于梯度信息的算法也有学者进行研究。赵新海等[6]利用B样条曲线构建预锻模具,将形状优化问题转化为参数优化问题,并用敏感性分析获得了最优模具形状。Badrinarayanan等[7]也对塑性成型过程中工艺参数的敏感性进行了分析,获得了最优工艺参数。此外,基于反向计算的算法也得到了广泛的研究。Gao等[8,9]使用反向模拟技术对叶片锻造的预成型进行了优化设计。但该方法脱模准则处理和初始速度场的求解比较困难的缺点限制了该方法的推广。
尽管这些研究对锻造工艺的优化设计具有一定的优化效果,然而代理模型因受到样本数量的限制而导致精度有限,特别是代理模型的外推预测精度更难保证。反向模拟方法的脱模准则又极难构建,基于敏感性分析的优化算法理论较为复杂,并且通用性较差;这些缺点都限制了这些方法的推广应用。本文提出了一种遗传算法与FORGE数值模拟软件直接耦合,并用克里金模型构建局部梯度的优化算法,FORGE作为成型工艺的求解器,遗传算法对工艺参数进行自动调整,进而通过遗传算法、FORGE软件和克里金模型之间的实时通信实现对克里金模型精度的不断修正,提高优化精度。
1 优化策略
1.1 设计变量
影响凸轮轴锻造成型质量、成型载荷、填充情况最重要的因素之一为坯料形状和尺寸。图1为某凸轮轴锻件的终锻情况。图1中的凸轮轴锻件具有中间3处凸起区域,分别为A,B,C。根据这类锻件的特征,可知在这3个区域中需要的材料更多,因此坯料的形状也应当具备3个区域凸起特征;根据凸轮轴锻件的形状初步设计出坯料的形状。

图1 某凸轮轴锻造结果
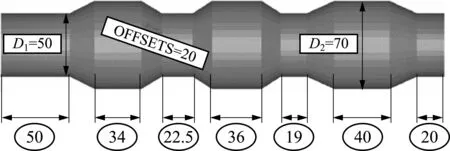
图2所示的坯料形状设计了3个变量作为优化设计变量,分别是D1,D2,D3。多个圆柱使用相同直径可减少设计变量的数目、多个斜面采用相同的尺寸也是为了减少设计变量的数目。3个变量的取值范围为:D1∈[40, 50],D2∈[60, 70],D3∈[15, 20]。
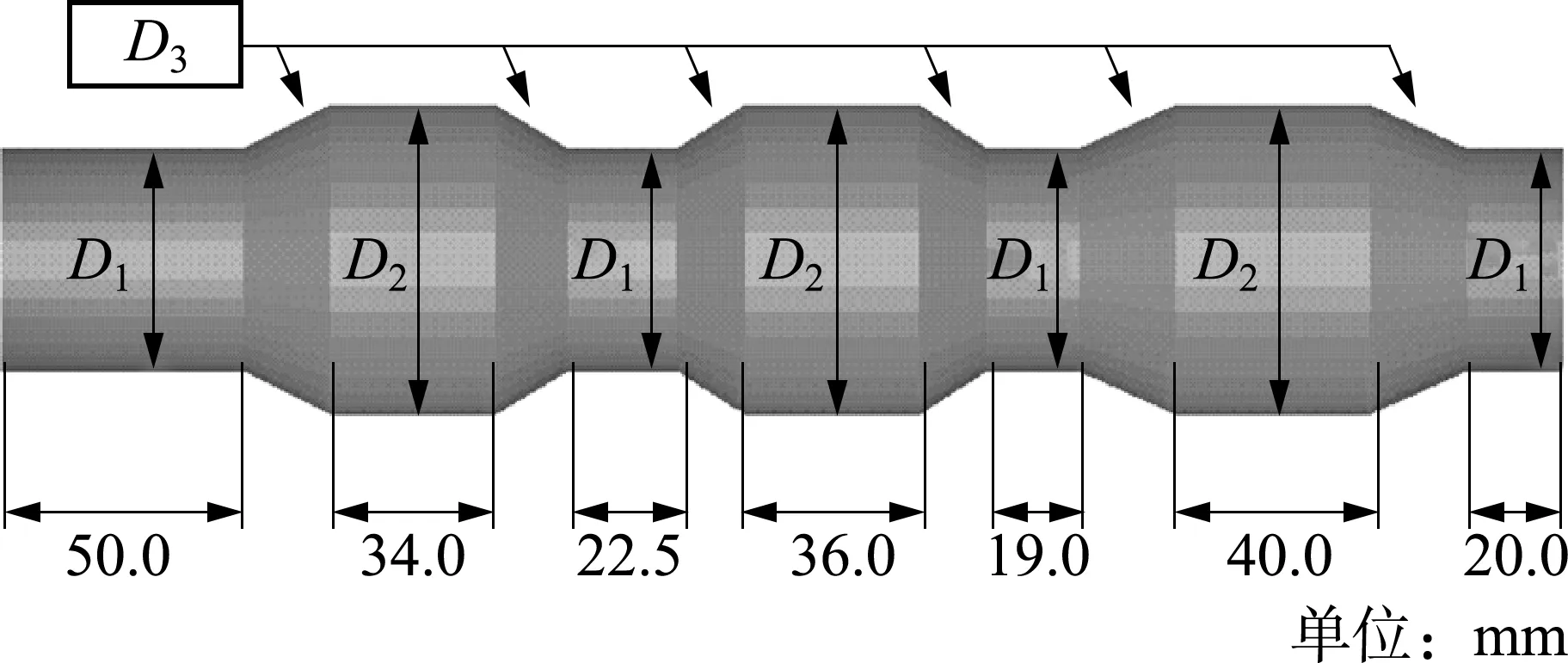
图2 坯料形状及其设计变量
1.2 目标函数构建
1.2.1 优化指标
在锻造工艺设计中,最理想的情况是坯料体积与锻件的体积相等,然而依靠经典设计方法通常会导致欠填充、折叠等锻造缺陷。因此,提出了基于优化理论的坯料设计方法。本研究的目的是在没有锻造缺陷的前提下,尽可能节省材料。因此其优化指标可以用如下公式描述:
(1)
其中,n是单元数目,Vi表示第i单元的体积,V表示锻件体积。优化的目标是在保证填充完整的情况下体积尽可能小。为了保证满足约束,将需要填充的空间表征出来。
1.2.2 约束条件
如图3所示的内部型腔区域为填充区域,该区域是模具除了飞边槽以外的曲面;优化过程中坯料必须在内部型腔区域接触,其原因在于坯料与模具接触即可证明接触区域已经填充。除填充约束外,折叠、应变均匀性、成型载荷也有可能作为约束条件。

图3 填充区域曲面
1.2.3 目标函数构建
带约束的优化问题,在可行解内寻优通常比较困难;当约束条件较为复杂时,即便构建可行,求解也是十分复杂的问题。为了充分发挥进化算法的优势,可将约束条件用惩罚法嵌入于目标函数中,如下所示:
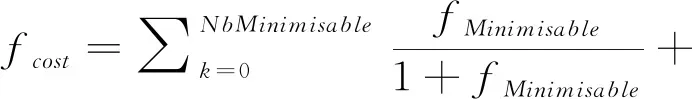
(2)
其中,NbConstraint表示不能满足约束的约束条件数目。fMinimisable优化目标,在本文中fMinimisable=Min(V),即表示坯料体积最小化。fConstraint表示约束条件函数,即填充百分比、折叠量的值。式(2)构建的目标函数是使用优化理论中的惩罚法将约束转化为目标函数的策略,该策略在优化过程中,不满足约束的参数组合目标函数值会较大,进而在优化过程中这些参数组合被逐渐淘汰,最终得到的优化参数将排除不满足约束的情况。
1.3 优化策略
基于传统的克里金模型和遗传算法的优化策略存在一个比较致命的缺陷,当克里金模型预测精度较低时,算法无法改进克里金模型。而基于遗传算法和有限元直接耦合的优化策略存在着另一个比较严重的问题,每一代所有个体计算适应度时由于需要调用有限元求解成型过程,其花费的时间较长,因此直接耦合策略对于3D问题极难在有效时间内获得最优解。
如图4所示,将遗传算法、克里金模型、数值模拟进行实时动态协同仿真优化,既可克服适应度函数计算时间过长的缺点,又可解决克里金模型存在精度不足的问题。在该策略中,当优化变量迭代到数值模拟未覆盖的空间时,调用数值仿真求解器在该变量空间进行适应度函数值的求解,进而降低在覆盖的变量空间重复调用数值仿真所花费的时间成本。此外,每一代最优个体直接调用数值仿真求解器以校验克里金模型。
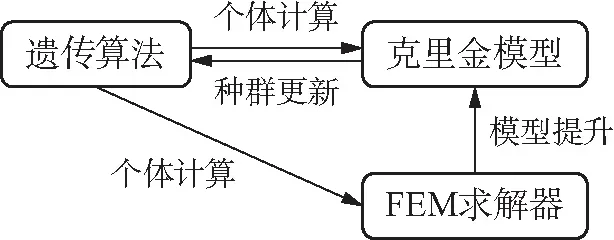
图4 基于克里金、有限元法和遗传算法的优化策略
如图5所示,本优化策略的执行过程为: 首先,初始化种群并调用Forge计算每个个体的成型过程,并调用约束和目标函数构建算法获得每个个体的适应度函数值(目标函数);随后,执行遗传算法的选择、交叉、编译操作并更新父种群。最后,在次计算种群各个个体的适应度函数,直至遗传算法满足结束条件。除初始化种群需要全部调用Forge以外,其余代的最优个体才会调用Forge进行结果校验,其他个体则直接使用克里金模型计算目标函数值。此外,当个体表征的变量在初始化种群代表的空间范围外部时,需要调用Forge进行适应度函数值计算。

图5 优化过程
2 优化实验
2.1 实验材料
优化实验选用的材料为42CrMo4,其成分如表1所示,合金中除铁元素外,含量最多的为Cr。其屈服强度为930 MPa左右,延伸率大于12%,断面收缩率大于45%,硬度小于217 HB。42CrMo4常用于制造要求较35CrMo钢强度更高和调质截面更大的锻件,如机车牵引用的大齿轮、增压器传动齿轮、后轴、受载荷极大的连杆、弹簧夹及凸轮轴等,42CrMo4也可用于2 000 m以下石油深井钻杆接头与打捞工具等。
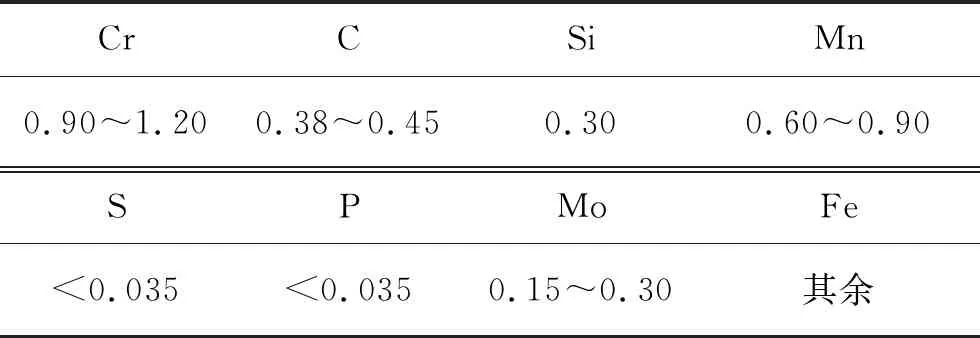
表1 42CrMo4的主要化学成分(质量分数) %
2.2 优化结果
对于遗传算法来说,其种群数目越多全局优化能力越强;然而种群数目增加时会显著增加计算成本。通常种群数目设置为变量个数的2倍。本遗传算法参数设置为: 种群数目为6,即每一代有6个个体,第一代需要6次有限元仿真。遗传算法个体间的交叉概率设置为0.8,变异概率设置为0.1。遗传算法的变异率越大,个体变异的概率越大,不容易陷入局部最优解,但获得全局最优个体所需要的计算成本也会大幅提升。优化变量的初始值设置为D1=50,D2=70,D3=20。此外,锻造温度设置为1 125℃。
2.2.1 坯料尺寸和锻件形状
图6为优化得到的最优坯料尺寸,锻件满足坯料体积最小、飞边较小、材料利用率高、成型质量比较好。初始坯料尺寸的体积为978 350 mm3,优化后的坯料体积为655 340 mm3,坯料体积减少了27.81%。优化后的设计变量取值为D1=40.6,D2=60.0,D3=16.6。
2.2.2 填充效果对比
体积最小化是优化的目标,体积最小且有效的前提是没有锻造缺陷。型腔充填完整是最重要的约束之一。如图7所示,用锻件表面接触情况来评判填充效果,优化前后填充效果有所差异,优化前的填充不均匀,特别是凸轮轴两个突出部位填充较差。而优化后的锻件填充均匀。这说明,约束条件在优化过程中发挥了作用,不满足约束的个体逐渐被淘汰。
(a) 优化前坯料尺寸

(b) 优化前锻件形状
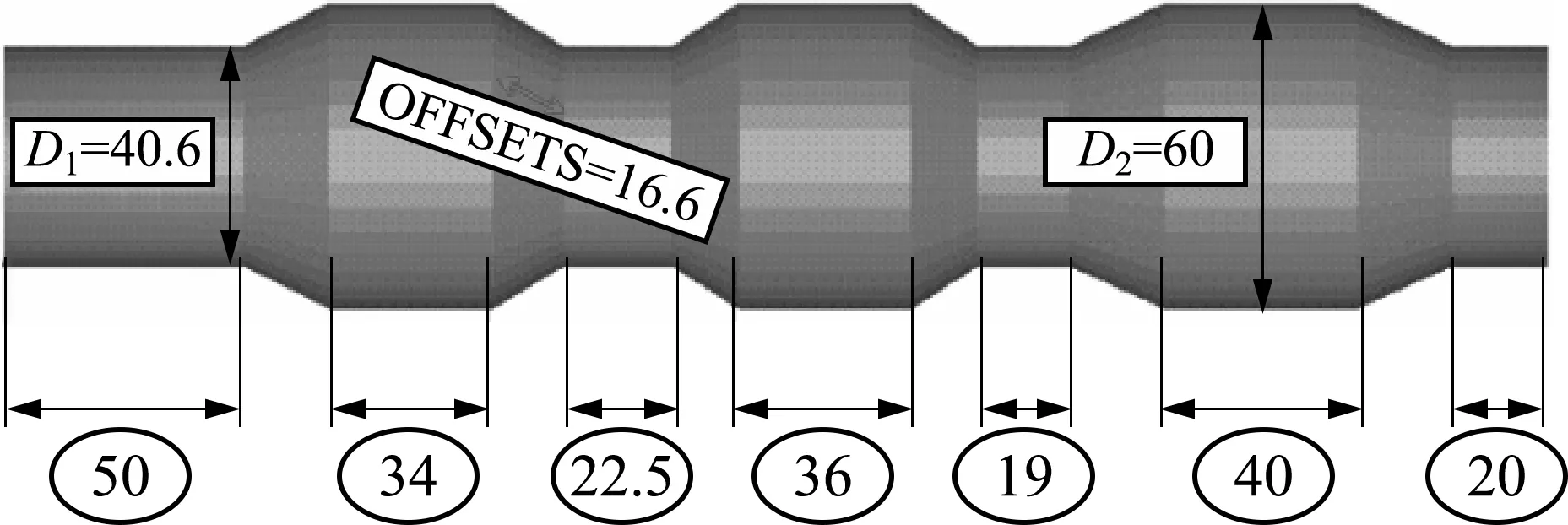
(c) 优化后坯料尺寸

(d) 优化后锻件形状
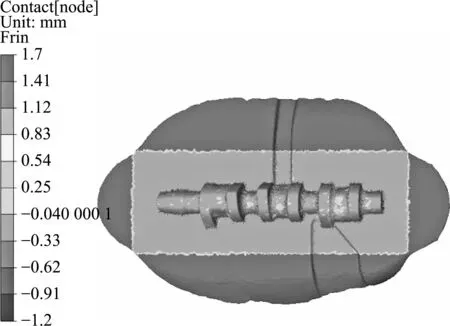
(a) 优化前坯料和模具接触情况

(b) 优化后坯料和模具接触情况
2.2.3 折叠情况对比
如图8所示,另一个比较重要的约束指标是折叠。优化前发生折叠倾向的区域比较多,特别是锻件靠近桥部区域的折叠倾向比较严重。优化后在锻件本体内不存在折叠倾向,锻件与型腔接触区域也不存在折叠倾向,优化效果明显。
2.2.4 成型载荷对比
如图9所示,下端曲线是优化后的成型载荷,上端曲线是优化前的成型载荷;优化前后成型载荷大约从4 200 t减小到1 200 t左右,成型载荷减小了大约71.43%。这是坯料形状不合理导致过多材料流向飞边槽,从而使得上模压下困难,成型载荷迅速增加。

(a) 优化前坯料折叠情况

(b) 优化后坯料折叠情况
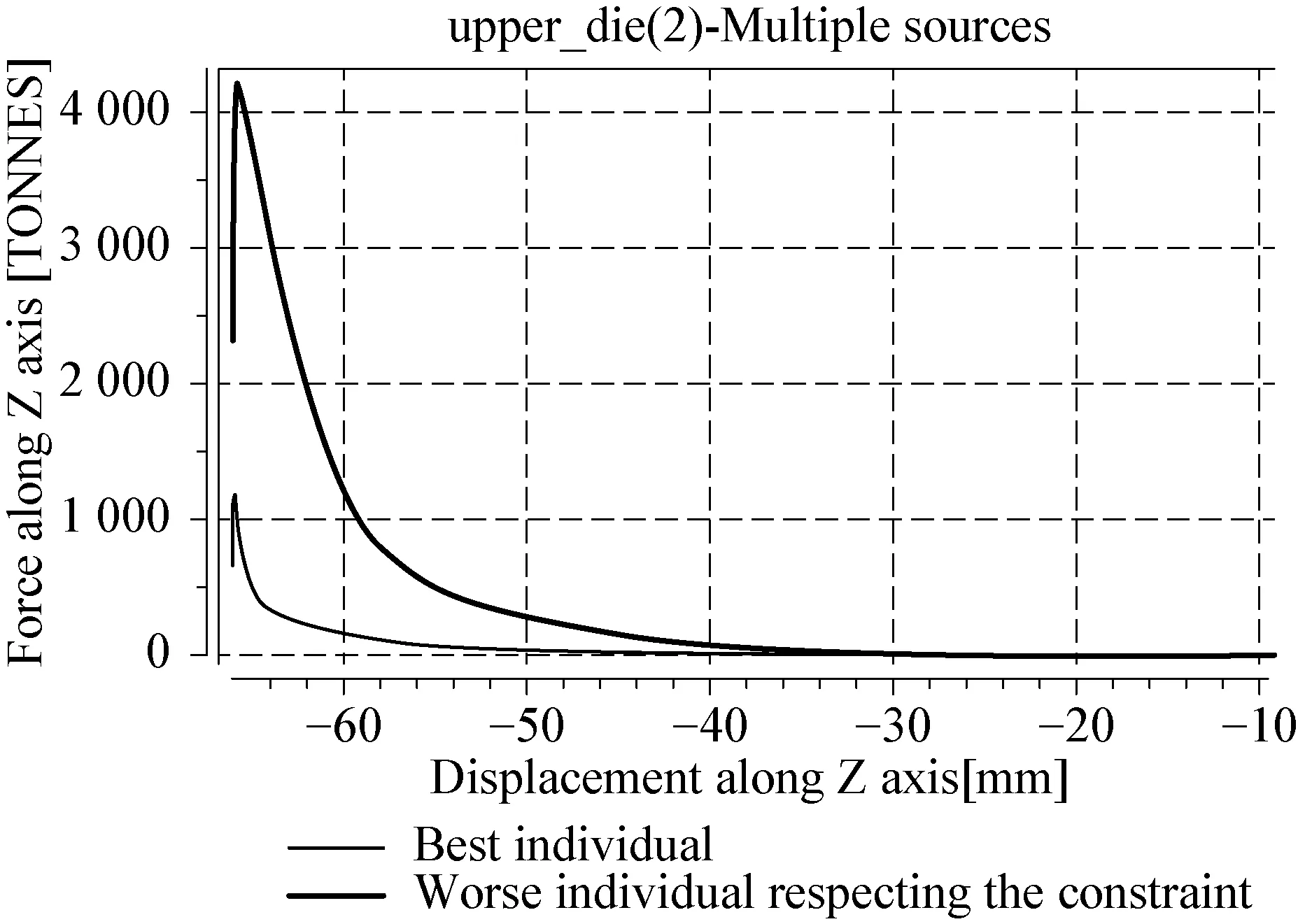
图9 优化前后载荷对比
3 结论
使用遗传算法、克里金模型和数值模拟直接协同优化的策略,对模锻坯料几何参数进行优化,得到如下结论。
1) 对锻件的形状进行分析,提出一种坯料形状,并选用3个尺寸参数作为优化参数,优化效果显著,可显著减少下料体积、节省材料27.81%。
2) 优化后的坯料能够满足充填完整约束、无折叠约束,并且优化后的成型载荷降低了大约250%,优化后的设计变量取值为D1=40.6,D2=60,D3=16.6。
3) 优化结果表明,充填性能、折叠情况、成型载荷都与坯料的形状和尺寸呈现出较强的相关性,并且充填、折叠、成型载荷之间存在一个指标比较好,其余指标也比较好的相关关系。
