重视数形结合 实现深度学习

于桂红 于振海

数形结合是一种重要的数学思想方法。数与形是数学中的两个最古老也是最基本的研究对象，他们在一定条件下可以相互转化。借助“数”的精准性，可以阐明“形”的某些属性。如我们给长方形具体的长和宽，给三角形边长、高，给圆半径等数据，通过数据的计算来研究这些图形的特征，即“以数解形”;借助图形来阐明数与数之间的某种关系，即“以形助数”。

无论是图形与几何、数与代数问题的解决，还是统计与概率问题的处理，都需要借助图形来使数变得更直观或者借助数来使图形变得更具体。在计算课的教学中，我们必须要重视数形结合思想的渗透，发展学生的数学思维能力，真正实现深度学习。

一、 分析学情，确立数形结合的关键点

计算贯穿于小学数学教学的全过程，与学生的数学学习始终相伴，它是每个学生必备的数学技能。当前，很多学生的计算能力明显下降，尤其是灵活计算的能力不足，这与学生没有充分理解算理有密切关系。小学生的学习规律一般分為五个阶段：激发动机、知识感知、知识理解、知识巩固、知识应用，其中，“知识理解”是核心。学生真正理解知识的标志，一是能用自己的语言或动作将知识正确地表述出来，并能用例子进行说明;二是当新知识以变式的方式呈现时，仍能掌握其实质;三是了解与其他知识的异同，并能把握知识的上下属关系。教师应遵循这一学习规律，夯实“知识理解”这一核心环节，提升学生的思维水平和能力，促使深度学习真正发生。

不同地域、不同班级学生已有的知识经验和心理认知特点都不尽相同，只有进行学情分析，找准学生学习的起点，才能根据学生学习活动的最近发展区，确定教学内容的难点和关键点。

北师版《义务教育教科书·数学》三年级上册第一单元“过河”与前几节课相比，出现了“小括号”的知识点。课前，可以这样进行前测。

1.计算：①60-30÷6，②（60-30）÷6，③27÷3+6，④27÷（3+6）。

2.小李要做60道口算题，已经做了32道，剩下的要在4分钟内完成，平均每分钟要做多少道？请列综合算式进行计算。你认为应该先算减法还是先算除法？为什么？

第1题中①和③两个小题是前几节课的知识，在笔者所教班级的30名学生中，有24人解答正确率达到了100%，其它6人这两道题均做错了其中一道。第1题中②和④小题有10人全部正确。经调查，是因为有些学生提前预习了。有5人选择放弃计算，有15人按照以往的经验先乘除，再加减的顺序进行计算。第2题中要求列综合算式，其中做对的学生只有2人，其他学生基本都写成了60-32÷4=28÷4=7（分）。

分析前测结果，我们发现，一是学生对于上节课的知识掌握得较好，受上节课知识迁移的影响比较大;二是虽然有三分之一学生做带小括号的计算题计算没有问题，但是他们并不能准确无误地将知识运用于问题的解决;还有一些学生在解决问题的过程中，虽然没有加小括号，但是都根据解决问题的逻辑关系即算理进行计算，并得出了正确的结果。这说明学生对于为什么要加小括号及小括号的作用是不理解的，由此我们确定了本节课学生学习的难点：体会小括号引入的必要性，理解，并掌握用小括号可改变运算顺序这一算理。

二、 分析教材，明确数形结合的语言表征方式

教师在阅读和分析教材时，要能够读懂编者对教学内容的具体要求，结合学生的实际情况来确定教学策略。《义务教育数学课程标准（2011年版）》在计算教学上提出：“应通过解决问题进一步培养学生的数感，增进算法的理解。”学生在解决问题的过程中，要把摆一摆、画一画、列表格等直观表征的方法转化为恰当、有逻辑性的语言表征方式，这实际上就是将数学思维外显化。鉴于小学生的年龄特点，他们的思维水平相对较低，思维外显对他们来说有一定难度。教师在备课的过程中，要先分析教材中要求的计算教学内容，发现具体教学内容所具备的数学特征，然后结合学生已有语言表征的特点，明确数形结合的语言表征方式，最终帮助学生明白算理。只有这样，才能有的放矢地帮助学生在体验算理的过程中感悟算法，发展思维。

北师版《义务教育教科书·数学》五年级上册“精打细算”的算理就是11.5除以5，用10元除以5等于2元，再把剩下的1.5元变成15角，15角除以5等于3角，2元加3角就是2.3元。在分析教材时要明确，这个算理是学生理解竖式计算方法的基础，要理清用哪种数形结合的语言表征方式可以把这个算理讲清楚、讲到位。实际教学中，可以让学生借助真实的人民币这个具体的“形”，将除法算理的表达过程用语言描述出来。这样，学生一方面能够通过真实的情境理解具体数字所代表的含义;另一方面，在说算理和组织语言的过程中，也能够感悟除法算理，发展数学思维。

同样，北师版《义务教育教科书·数学》五年级下册“分数乘法（三）”的算理是[3/4]乘以[1/4]，把一个长方形平均分成4份，其中的3份涂上颜色表示这个长方形的[3/4]，再把涂色部分平分成4份，其中一份就占这个长方形的[3/8]。教师必须在充分读懂教材要求的基础上，让学生通过画图或者折纸，讲出算理得出的过程。这一算理，是五六年级学习“分数应用题”这一单元中的“分数乘法”时分数单位转换的基础，学生只有理解了这一算理，在以后做分数乘法应用题转换单位“1”的时候，才不会在心里打一个大大的问号：为什么这样一乘，单位“1”就变了呢？

三、抓住本质，实现“数”与“形”的有机结合

《义务教育数学课程标准（2011年版）》指出，数学教学应“重视学生已有的经验，使学生体验从实际情境中抽象出的数学问题、建构数学模型、寻求结果、解决问题的过程。”可见，情境只是实现数学知识抽象化的一个直观支撑，为了情境而情境的教学只会影响实际教学效果。教师只有抓住知识的本质进行恰当地点拨，才能“挠”到学生的“痒处”，实现“数”与“形”的有机结合。

北师版《义务教育教科书·数学》五年级上册“精打细算”一课中，当我们把数学问题抛给学生的时候，他们一定会用很多方法解决，这时教师就需要到学生中巡视，把不同的方法展示到黑板上。实际上，用算理来解决问题的学生并不多，多数学生经过多年的训练，一定会用竖式去做，但做法有对有错。这样一来，教师就要把多种有价值的做法都展示到黑板上。学生汇报的时候，要有选择地安排学生进行汇报，先安排用算理的学生做汇报，然后安排用竖式算错的学生汇报，最后安排用竖式算对的学生汇报。在汇报的过程中，教师一定要鼓励学生不懂就问，有的学生能问到关键点，问不到也没有关系。我们要抓住四个关键问题：整数部分算完余下的1表示什么？小数部分余下的5表示什么？明明余下了1.5元，竖式里为什么写15，而不写小数点呢？“商”为什么写小数点呢？其中后面的两个问题直接抓住了知识的本质，指向算理。这样一来，通过几个问题，引领学生完成了数形结合，提升了思维品质的深刻性和灵活性。

此外，二年级上册“有多少点子”一课的教学目标是通过计算点子的数量进一步体会加法和乘法之间的联系，其知识的本质就是对乘法意义的理解并灵活运用。乘法的意义是求几个相同加数和的简便运算。在引导学生处理“问题串”的时候，学生摆出了7行4列或者是4行7列。无论怎样摆，都是4个7相加或7个4相加。这时，教师应相机板书：

7+7+7+7=28 4个7 4×7 或 7×4

4+4+4+4+4+4+4=28 7個4 4×7 或 7×4

让学生观察板书并提问：“你发现了什么？”这里面的信息量很大，学生会发现，无论是4个7相加还是7个4相加都可以用两个相同的算式表示。这时，需要教师点拨：“看第一行，在这里，4个7中，7表示加法算式中的什么？4表示什么？算式4×7中7表示什么？4表示什么？”这样的点拨，紧紧围绕乘法意义这一本质进行教学，使学生明白了4×7在不同情况下表示不同的意义。意义不同，都可以用相同的算式表示。

四、去情境化，实现数形结合的抽象建模

学生学习数学需要一个先“内化”再“泛化”的过程，要通过大量的例举，在观察、比较、分析、抽象、概况的数学活动中，将数学知识从具体情境中抽象出来，由现实情境走向数学，实现对现实情境的超越，建立数学模型;再反过来，将自主建构的知识运用于新的情境，解决新的问题。

北师版《义务教育教科书·数学》四年级上册“乘法分配律”这一知识点，就要经历以下建模过程。

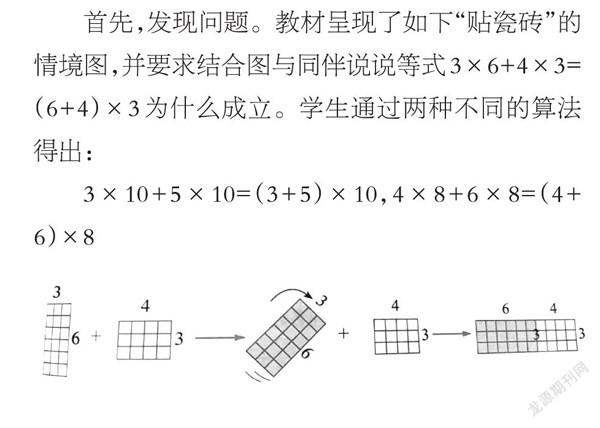
首先，发现问题。教材呈现了如下“贴瓷砖”的情境图，并要求结合图与同伴说说等式3×6+4×3=（6+4）×3为什么成立。学生通过两种不同的算法得出：

3×10+5×10=（3+5）×10，4×8+6×8=（4+6）×8

学生对规律的观察、理解、分析必须要有一个量的积累，才会实现质的飞跃。教材只提供这一个情境，教师如果在这里急着总结乘法分配律的规律显然为时过早。因此，可以再提供一个情境问题拓展学生的感知。

学校要给28人的合唱队买服装。每件上衣46元，每件裤子54元，一共需要多少元？

学生会列出两个不同的算式，并发现这两个算式可以用等号连接：46×28+54×28=（46+54）×28。在前面两个情境的基础上，教师还可以引导学生观察等号两边的算式，并提问它们有什么特点？

其次，验证规律。要求举例验证符合上面规律的算式就一定相等。

再次，归纳规律。让学生自己总结和归纳上面得出的规律。

最后，运用规律。这时，可以出示拓展类的题型，学生在运用规律的同时，学会举一返三，真正达到对规律的理解。

建构主义认为，知识并不是简单地由教师或其他人传授给学生，只能由每个学生依据自身已有的知识经验，主动地加以建构，最终形成属于他们自己的数学知识体系。因此，教师必须引导学生从复杂的现象中抽象出它们最本质的数学模型，实现从方法到模型，从模型到应用的转变。

总之，数学是抽象和形象相结合、严谨和直观相统一的课程，在小学、中学乃至高中的整个数学知识体系中，数形结合思想方法始终贯穿其中，它不仅是一种思想方法，更是我们进一步学习、解决、探索和研究数学问题必备的能力。鉴于数形结合的重要性及其意义，教师一定要重视并善于在课堂上进行数形结合思想的渗透，最终实现学生的深度学习。

（责任编辑：杨强）