Performance improvement of the stochastic-resonance-based tri-stable energy harvester under random rotational vibration

Tingting Zhng, Ynfei Jin,*, Ynxi Zhng

a Department of Mechanics, Beijing Institute of Technology, Beijing 100081, China

b Department of Mathematics, Xi’an University of Science and Technology, Xi’an, Shaanxi 710054, China

Keywords:Tri-stable energy harvesting Stochastic resonance Random rotational vibration Signal-to-noise ratio

ABSTRACT In this paper, the stochastic-resonance-based tri-stable energy harvester (TEH) is proposed to enhance harvesting performance under random rotational vibration. An electromechanical coupled system interfaced with a standard rectifier circuit driven by colored noise is considered. The stationary probability density function (SPDF) of the harvester is obtained by the improved stochastic averaging. Then, with the adiabatic approximation theory, the analytical expression of signal-to-noise ratio (SNR) for the TEH is deduced to characterize stochastic resonance (SR). To enhance direct current (DC) power delivery from a rotational TEH, the influences of system parameters on SR is discussed. The obtained results suggest that there are damping-induced resonance and noise-intensity-induced SR in the tri-stable system. The TEH has higher harvesting performance under the optimal SR. That is, the optimal parameter combinations can induce optimal SR and maximize harvesting performance. Thus, the stochastic-resonance-based TEH can be optimized to enhance energy harvesting through choosing the optimal parameter.

The vibration energy harvesting has been widely concerned by many scholars as a possible solution for continuous power supply of low-power electronics [1–5]. For instance, Liu et al. [1] proposed a new quasi-conservative stochastic averaging for nonlinear vibration energy harvesters (VEHs) driven by Gaussian colored noise. They [3] further investigated the stochastic dynamics of a bi-stable VEH under filtered Gaussian white noise by combining an improved coordinate transformation. In recent years, the development of wireless sensor nodes for rotational equipment has attracted an increasing attention on energy harvesting from rotational motion [6–10]. For example, Hsu et al. [6] presented a comprehensive design of a passively self-tuning composite cantilever beam for energy harvesting under rotational motion to improve power output performance. Green et al. [8] established the model of rotational energy harvester in a probabilistic manner by exploiting experimental data combined with Bayesian approach. Unfortunately, the previous investigations of tri-stable energy harvesters(TEHs) under rotational vibrations tend to ignore the effect of random excitation on system dynamics, which will result in a mismatch with the actual situation. Furthermore, the neglect of the nonlinear harvesting circuit makes the harvested alternating current incapable of powering electronics. Therefore, motivated by the above reasons, the TEH interfaced with a standard rectifier circuit under random rotational environment is considered in this paper.

Stochastic resonance (SR) is often described the phenomenon that the response of a nonlinear dynamical system to a weak periodic signal is enlarged by adding an optimal dose of noise intensity[11]. Many researches [12–17] have shown that SR can be used to enhance the harvesting efficiency of nonlinear multi-stable VEHs.For example, Jin et al. [13] focused the enhancement of tri-stable energy harvesting by using SR. They found that the harvesting performance under the SR effect was much higher than that obtained under stochastic vibration alone. Fezeu et al. [14] investigated the dynamical analysis and ghost-stochastic resonance of a hybrid energy scavenger under the white noise based on stochastic averaging. Kim et al. [16] proposed a self-tuning SR energy harvester based on centrifugal stiffening effect for rotating systems under modulated noise, which achieved greater power and wider bandwidth. In short, the SR mechanism can be utilized for the optimal design of nonlinear VEHs to enhance harvesting capacity. Therefore, the SR is employed in this paper to improve tri-stable energy harvesting from random rotational vibration.

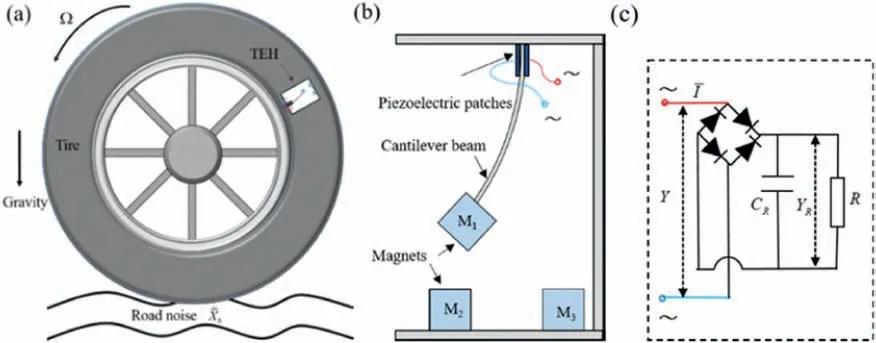
Fig. 1. (a) The tri-stable energy harvesting device installed on the wheel. (b) Schematic diagram of the TEH. (c) Standard rectifier circuit connected to the TEH.

In Fig. 1, a TEH interfaced with a standard rectifier circuit is considered, which is mounted on the hub to harvest DC power from random rotational motion. During vehicle driving, the TEH is autonomously excited by road noise and harmonic excitation which is caused by rotational motion and the magnet gravity.The AC power harvested by the TEH is converted into DC energy for supplying electronics through the rectifier circuit in Fig. 1c. It should be pointed out that the TEH driven by colored noise rotates under various constant rotational speeds. The dimensionless governing equation of the electromechanical coupled TEH can be expressed as [10,18]

in which,Xis the dimensionless displacement.Ωis the dimensionless angular velocity of rotational motion. The linear stiffness coefficientk1=1+γ Ω2depends on the rotational speedΩ, whereγis the coefficient of coupling termΩ2. Obviously,k1can be changed through the rotational speed besides the adjustment of the magnet spacing. Thek3,k5are the dimensionless cubic and quintic stiffness coefficients. Theβandκare the dimensionless damping and electromechanical coupling coefficient respectively.TheIdefines the dimensionless current flow. TheYandYRare the dimensionless piezoelectric voltage and rectified voltage. Theαdenotes the time constant ratio. Theλis the ratio of filter capacitance to the internal capacitance of piezoelectric patches. Moreover, theFis the exciting force caused by the gravity of the tip magnet mass. Theξ(t)is the colored noise with intensityDand correlation timeτ, which is employed to simulate road noise.

Obviously,g(t) =ξ(t)cos(Ωt)is a non-stationary random process with autocorrelation function 〈g(t)g(s)〉≈D/(2τ)cos[Ω(ts)]exp(-|t-s|/τ). To obtain the approximate solution of system(1), the stochastic harmonic processη(t)with weak-stationary randomness is used to replace the modulation noiseg(t). Specifically described as

To design the stochastic-resonance-based TEH, the analytical expression of the SNR is derived in this section based on the steadystate PDF of the harvesting system.

Due to the symmetry of potential function, the transition rates from wells1tos2and from wells3tos2are the same, that is,k1,2=k3,2. Similarly,k2,3=k2,1. The Taylor expansion with small parameterFcos(Ωt) is executed in Eq. (15), and the first nontrivial order is retained as

wherePo=〈καY2〉 is the mean power harvested from random rotational motion.PI=〈 ˙XFcos(Ωt)+ ˙Xη(t)〉 denotes the mechanical energy of random rotational vibration. 〈·〉 represent the time average and ensemble average.

To enhance performance of TEH from random rotational vibration, the effects of system parameters on SNR in Eq. (17) will be discussed. Note that the obtained rectified voltage is close to constant if the filter capacitor of the standard rectifier circuit is large enough. In the following analysis, the parameters are fixed asF= 0.01,τ=0.1 andλ= 100.

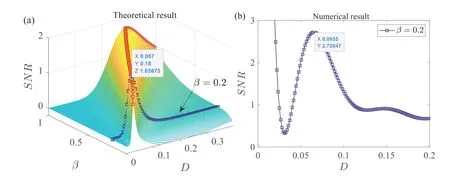
Fig. 2. SNR is plotted as a function of D and β. (a) Theoretical result: blue square curve is the variation of SNR with D for β = 0.2, and the curve with the red hollow circle is the SNR peak. (b) Numerical result is obtained by SNR = 10log10(Ps / Pn)dB. Ps is the spectrum value at signal frequency in the output power spectrum, and Pn denotes the average of the remaining output power spectrum value. Other parameters are chosen as Ω=0.1, k1 = 1.2, k3 = -2.8, k5 = 1, κ = 0.1, α = 0.05.

Fig. 3. SNR as a function of β under different (a) k1 for fixed Ω=0.1. (b) Ω with k1 =1+γ Ω2 and γ = 20. The other parameters are k3 = -2.8, k5 = 1, D = 0.09, κ = 0.1,α = 0.05.

In Fig. 2, the SNR is plotted as a function ofβandD. For a specificβ(such as the blue curve, that is,β= 0.2), asDincreases,the SNR first increases to the maximum and then decrease. This phenomenon indicates the occurrence of noise-induced SR. It is observed that with the increase ofβ, the peak of SNR first rises and then falls, and its position gradually moves to the large noise intensity, that is, optimal intensity noise for SR is increased. The combination (D,β) marked by the red curve in Fig. 2 can be chosen to induce SR and enhance energy harvesting. In Fig. 2b, the variation of SNR withDforβ= 0.2 is numerically plotted. Obviously, with the increase ofD, SNR reaches a peak nearD= 0.0655,which is consistent with the theoretical result in Fig. 2a.

Figure 3 depicts the variation of SNR withβat differentk1andΩ, respectively. In Fig. 3a, with the increase ofβ, the SNR has a single peak at which the optimal SR is induced. Fork1≤1.2, the peak decreases slightly and shifts to the left ask1increases. Whenk1continues to increase, the peak decreases rapidly and its position remains almost unchanged. Moreover, forβ ＜βk1, ask1increases under a specificβ, the SNR first increases and then decreases, that is, an optimalk1optexists to maximize SNR. For example, whenβ= 0.2, the SNR has a single peak with the increase ofk1, in this case,k1opt= 1.2. In Fig. 3b, whenβ ＜βΩ, the SNR exhibits similar variation characteristics, that is, there will be aΩinduced SR. In general, it can be speculated that in the interval of [0, βk1] or [0, βΩ] under a specificβ, an optimalk1orΩ(i.e.,k1opt= 1.2 orΩ1opt= 0.12) can be found to induce optimal SR. Notably, the influence of rotational motion is considered in model (1),which is embodied in the linear stiffness coefficientk1=1+γ Ω2.This means thatk1of TEH can be adjusted by choosing an appropriate rotational speedΩfor performance improvement.

In Fig. 4, the variation of the SNR withDunder different nonlinear stiffness coefficients is plotted. It is seen that the SNR peak first increases and then tends to flatten with decreasingk3. Whenk3≤-3, the peak with an almost constant value moves towards small noise intensity. This means that under the premise of satisfying the tri-stable state, a smallerk3is positive to induce SR under low-intensity noise. In Fig. 4b, the peak decreases ask5increases, which suggests thatk5plays a negative role in inducing SR. In addition, forD ＞Dk3(in Fig. 4a) orD ＜Dk5(in Fig. 4b), the SNR always has a peak with the increase ofk3ork5, where the optimal SR can be induced. This indicates that for a fixedDunder a certain range, there is an optimal cubic or quintic stiffness coeffi-cient (i.e.,k3opt= -2.7 ork5opt= 1.0 in Fig. 4) to optimize harvesting performance.

The SNR as a function ofβunder differentκorαis plotted in Fig. 5. Asκincreases, the position of SNR peak moves toward the direction of decreasing damping while the peak decreases continuously. Moreover, the variation of SNR withκorαunder a specificβis analyzed. In Fig. 5a, forβ ＞β2, the SNR decreases asκincreases. On the interval [β1,β2]orβ ＜βα, for a fixedβ, the SNR first increases and then decreases asκorαincreases, respectively.For example, whenβ= 0.2, there is an optimalκorα(i.e.,κopt=0.15 orαopt= 0.15 in Fig. 5) that makes the SNR reach its peak. It is concluded that for a fixedβon interval [β1,β2] or [0,βα], there is always an electromechanical coupling coefficientκor a time constant ratioαthat can induce the optimal SR to enhance harvesting performance.

Figure 6 illustrates the effects of system parameters on the RMS voltage (Vrms) and power conversion efficiency (ρ%). In Fig. 6a, asDincreases,Vrmsfirst increases and then decreases, that is, there is an optimalDto maximize the rectified voltage. Theρ% has a single peak asβincreases, which is consistent with the variation of SNR in Fig. 3. Moreover, it is observed that forκopt= 0.15,αopt= 0.05 (see Fig. 5a) andκopt= 0.10,αopt= 0.15 (see Fig. 5b), theVrmsis much higher than that in other cases. Similarly, in Fig. 6b,ρ% has a higher level fork1opt= 1.2,Ωopt= 0.10 (see Fig. 3a) andk1opt= 1.3,Ωopt= 0.12 (see Fig. 3b). Thus, it is inferred that the TEH has higher harvesting performance when the optimal SR is induced. That is, the harvesting performance of TEH can be improved through choosing optimal SR parameters.

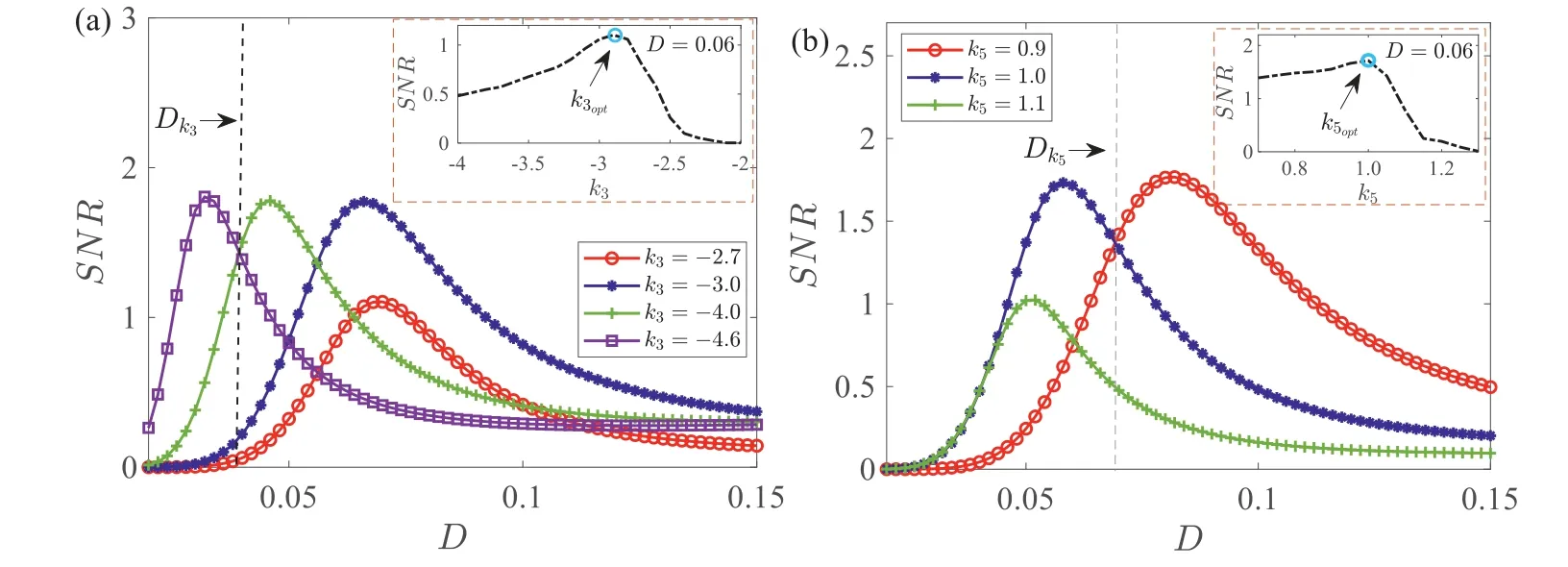
Fig. 4. Effects of nonlinear stiffness coefficients on SNR. (a) Fixed k5 = 1. (b) Fixed k3 = -2.8. The other parameters are Ω=0.1, β = 0.2, κ = 0.1, α = 0.05, k1 = 1.2.

Fig. 5. SNR as a function of β under different (a) κ for fixed α = 0.05. (b) α for fixed κ = 0.1. The other parameters are Ω=0.1, k1 = 1.2, k3 = -2.8, k5 = 1, D = 0.09.

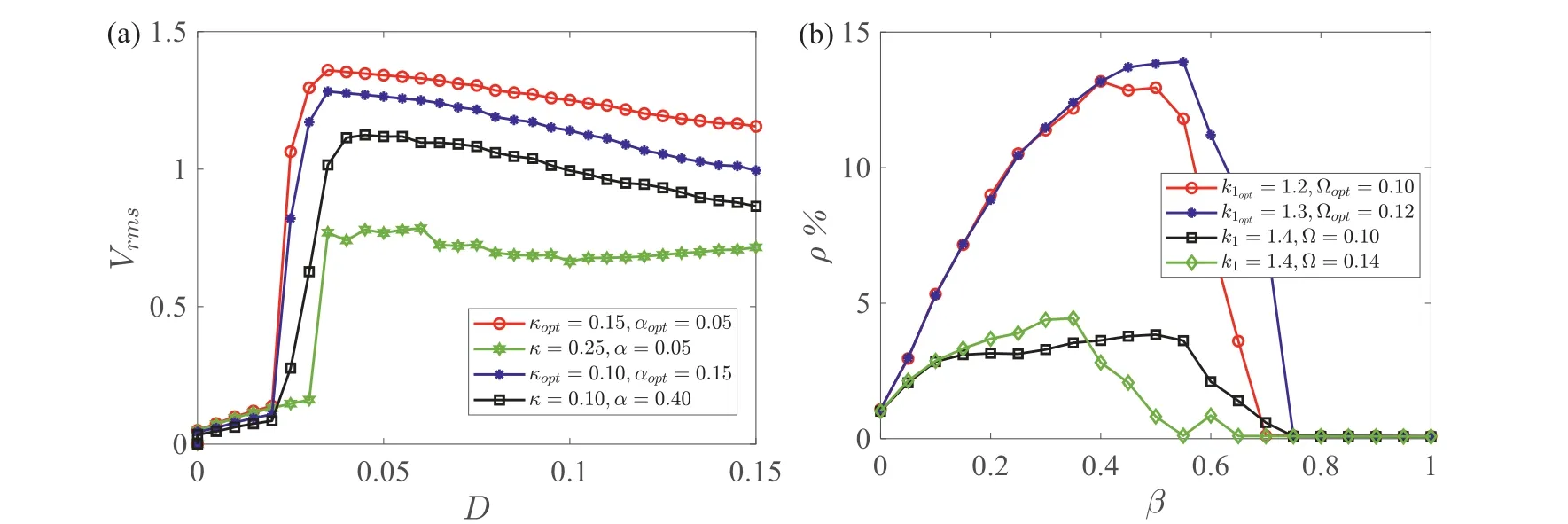
Fig. 6. (a) The Vrms varies with D at β = 0.2, k1 = 1.2, Ω = 0.1, k3 = -2.8, k5 = 1. (b) ρ% as a function of β by fixing D = 0.09, κ = 0.1, k3 = -2.8, k5 = 1, α = 0.05.

In this paper, harvesting performance of a rotational TEH interfaced with a standard rectifier circuit is studied by considering colored noise. The stochastic averaging based on energy-dependent frequency is exploited to derive the SPDF and generalized potential function. In the adiabatic limit, the theoretical expression for the SNR is derived to quantify SR. Then, the influences of system parameters on harvesting performance and SR effect are explored in detail. It is found that noise-induced resonance and dampinginduced resonance occur in the TEH. The optimal SR effect can be induced by choosing appropriate rotational speed, time constant ratio and electromechanical coupling coefficient to improve performance. The optimal parameter combinations are determined through optimal SR to maximize the power conversion efficiency and RMS voltage. Moreover, the optimal nonlinear stiffness coefficients can be found by adjusting the magnet spacing to optimize output performance while the optimal linear stiffness coefficient can be obtained by choosing an appropriate rotational speed. Therefore, a stochastic-resonance-based TEH is designed under random rotational vibration to maximize the RMS of the rectified voltage and enhance the harvesting performance.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

This work has been supported by the National Natural Science Foundation of China (Grant No. 12072025), Beijing Natural Science

Foundation (Grant No. 1222015), and the Natural Science Basic Research Program of Shaanxi Province (Grant No. 2022JQ-044).