Hydrothermal analysis of hybrid nanofluid flow on a vertical plate by considering slip condition

M.R. Zngooee, Kh. Hosseinzdeh, D.D. Gnji

a Department of Mechanical Engineering, Payamenoor University (PNU), Tehran, Iran

b Department of Mechanical Engineering, Babol Noshirvani University of Technology, Babol, Iran

Keywords:Hybrid nanofluid Stagnation flow Velocity slip Temperature slip

ABSTRACT Hybrid nanofluids have attracted burgeoning attention owing to their outstanding capacity to improve heat transfer. The influence of velocity and temperature slip parameter and nanoparticls’(NPs’) volume fraction on a vertical plate in the existence of suction has been explored in this work. The investigation’s controlling partial differentiation equations were transformed into a conventional differential equation mechanism using resemblance modifications. Equations were then solved employing the fifth-order Runge-Kutta method. The skin coefficient of friction, temperature, and temperature gradient all rise when the volume percentage of NPs increases from 0 to 2%. Furthermore, a rise in the temperature slip variable was linked to a drop in the Nusselt number (heat transfer).The Nusselt number increased 0.15% and 5.63% respectively when the velocity slip parameter enhanced from 0 to 5 and the NPs volume percentage were increased from 0 to 1.5%. Furthermore, an increase in the temperature slip from 0 to 3 inflated the x-direction skin friction coefficient 8.2%, while inflation in the velocity slip from 0 to 5 was associated with a decline in the x-direction skin friction coefficient 95%.

Today, the improvement of heat transfer is a sought-after subject for industries and researchers. In this regard, a wealth of techniques has been explored to inflate heat transfer such as increasing the heat transfer surface and surface of blades, vibrating heated surfaces, and so on. The next technique to inflate heat transfer is to use nanofluids. Nanofluids consist of nanoparticles (1-100 nm) and a base fluid. Choi and Eastman [1] presented the notion of nanofluid for the first time in 1995. In 2006, Tiwari and Das[2] studied the nanofluids’behavior in a two-sided square chamber and solved the transfer equations by the finite volume (FVM)method. Nadeem et al. [3] studied the three-dimensions flow of water-based nanofluid on an exponentially extending surface and investigated the different variables’impacts such as exponential temperature parameter, stretching parameter, and volume particle of nanoparticles (NPs).

Lund Baloch et al. [4] considered a Buongiorno model for nanofluids to obtain all nanofluid flow solutions on stretched surfaces. They further explored the effect of various variables on temperature, rate, concentration profile, the skin friction coefficient,Sherwood number (Sh), and Nusselt number. Hashemi et al. [5]investigated magnetic nanofluid natural convection in a permeable media compartment. They found that the entropy production and the Nusselt number are increased directly with a rise in the Rayleigh number and Darcy number in the laminar regions, while both of them have a reverse relationship with the Hartmann number. In addition, the middle Nusselt number was raised with a growing Darcy number in the turbulent region. Molana et al. [6]studied a novel geometric shape porous cavity containing Fe3O4-H2O nanofluid flow with realistic convection within a magnetic domain. They deduced that the heat transfer speed directly relates to the Hartman number and, thus, the magnetic field can strongly control heat transfer inside the cavity. In 2020, Dogonchi et al. [7] investigated the effect of geometric factors of NPs on the natural convection in an annulus among a wavy circular cylinder and a rhombus section subjected to a constant magnetic specialization. The results showed that the heat transfer speed and the middle Nusselt number increased with a given increase in Darcy and Rayleigh numbers. In addition, growth in the Rayleigh number further increased the nanofluid velocity while the aspect ratio of the wavy circular cylinder showed quite different behavior. Several numerical and experimental studies on the properties of nanofluids have been reported [8–14].

Nomenclature Roman letters a Flow strength Cfx,Cfy Skin friction coefficient in the x- and y- directions CP Specific heat at constant pressure (J/(kg·K))fw Suction parameter Grx Local Grashof number K Temperature jump coefficient k Thermal conductivity of the fluid (W/(m·K))L Characteristic length Nux Local Nusselt number(ρCP) Heat capacity of the fluid (J/(m3·K))Pr Prandtl number Re Local Reynolds number S Coefficient of the slip t Time (s)T Hybrid nanofluid temperature (K)T∞ Ambient temperature (K)Tw Surface temperature (K)T0 Base temperature (K)u,v,w Velocities component in the x-, y - and z - directions (m/s)x,y,z Space coordinates (m)Greek symbols η Similarity variable θ Dimensionless temperature λ Velocity slip parameter γ Temperature slip parameter Λ Mixed convection parameter μ Dynamic viscosity of the fluid (kg/(m·s))υ Kinematic viscosity of the fluid (m2/s)ρ Density of the fluid (kg/m3)β Thermal expansion φ Nanoparticle volume fractions Subscripts f Base fluid hn f Hybrid nanofluid s1 Solid component for Al2O3 (alumina)s2 Solid component for Cu (copper)∞ Condition outside of the boundary layer Superscript′ differentiation with respect to η

Several numerical investigations have aimed to increase heat transfer using hybrid NPs instead of single NPs. A hybrid nanofluid exists as a basic fluid blended with two or more solid NPs. Oztop and Abu-Nada [15] studied fluid flow and heat transfer using various nanofluids in a heating chamber. The results revealed that for different Rayleigh numbers, the standard Nusselt number grows directly with the nanoparticles’volume particle in the fluid. In addition, heat transfer was much higher when using the nanofluid in lower fractions than in higher fractions. Takabi and Salehi [16]studied the slow laminar convection in a sinusoidal chamber with a heat origin in the lower wall containing water-aluminum oxide nanofluids and a copper-aluminum oxide-water hybrid nanofluid.Their study investigated the impacts of Rayleigh number and concentration of nanofluid or hybrid nanofluid on temperature field and heat transfer. It was found that for each Rayleigh numbers,hybrid nanofluids possess better heat transfer and thus elevated cooling efficiency and lower surface temperatures. In addition, the rate of heat transfer inflation was significant at higher Rayleigh numbers and elevated volume fractions. Devasenan and Kalaiselvam [17] assessed the behavior of the hybrid nanofluid heat transfer in tubular heat exchangers, the effect of forced convection characteristics, thermal conductivity, and heat transfer coefficient, and estimated the volume fraction in which the heat transfer coeffi-cient is maximum. In their 2019 numerical study, Hosseinzadeh et al. [18] studied a solidification method of hybrid nanoparticles by altering the material in the thermal energy storage system with the snow crystal structure. The results revealed that at a volume fraction of 4% for hybrid NPs, the solidification rate increases by 24%. Talili et al. [19] studied a rectangular single-phase circulation loop containing water/Al2O3/Cu as a nanofluid. They investigated the effect of cooling length, heating length, pipe diameter, ring height, the concentration of NPs, etc., and found that the heating power, height, and diameter of the mass flow ring will increase with a rise in the concentration of NPs. Davi and Anjali Devi [20] studied a novel type of hybrid nanofluid to increase heat transfer through the boundary layer. Compared to pure water and nanofluid, the hybrid nanofluid has a more elevated Nusselt number. Additionally, the heat transfer rate was much more when adding the hybrid water/Al2O3/Cu nanofluid than pure water and nanofluid. In a numerical study, Waini et al. [21] examined the hybrid nanofluid flow and heat transfer on the exponentially shrinking surface and reported that heat transfer and the skin friction coefficient increase with the increment in copper volume particle and magnetic factor. In addition, increased radiation was found to diminish the surface temperature, culminating in a reduced heat transfer rate. Kashi et al. [22] studied the flow of water/Al2O3/Cu hybrid nanofluid on a stretching/shrinking sheet under the velocity slip impact and convection and deduced that variation in the Biot number has no impact on the boundary layer. A rise in the velocity slip and Biot number inflated heat transfer speed, whereas the reverse outcome was received with a rise in the volume fraction of Cu NPs. In a similar study, Abu Bakar et al. [23] examined the hybrid nanofluids flow on a stretching/shrinking permeable sheet considering the slip effects and radiation parameters.To do so, they employed a Cu-water and the water/Al2O3/Cu hybrid nanofluid and found higher heat transfer upon utilizing hybrid water/Al2O3/Cu nanofluids. In their numerical research, Kashi et al. [24] investigated the convection flow of the water/Al2O3/Cu nanofluid across a vertical sheet and reported that using hybrid nanofluids defer the separation point. In addition, both heat transfer and surface friction coefficient were much higher in the hybrid nanofluid than in pure water and a water and copper combination.Similarly, Kashi et al. [25] studied the Marangoni convection flow and the heat transfer of a hybrid water/Al2O3/Cu nanofluid on a stretching/shrinking surface. It was discovered that increasing the volume percentage of Cu for decreasing flow and the Marangoni factor for stretching flow boosts heat transmission considerably.The Marangoni factor and the volume percentage of Cu, on the other hand, might delay the boundary layer detachment procedure.In 2020, Kashi et al. [26] studied the heat transfer of the hybrid water/Al2O3/Cu nanofluid on the moving sheet with melting heat transfer. It was revealed that the hybrid nanofluid facilitates the separation of the border layer under melting heat transfer conditions, with the heat transfer speed that was more elevated for the hybrid water/Al2O3/Cu nanofluid compared to pure water and water/Cu. In addition, a rise in the melting parameter was found to diminish the heat transfer speed and accelerate the border layer detachment. Considerable researches have focused on the thermophysical properties of hybrid nanofluids [27–37].

Stagnation point flow is a subject of interest for many researchers. It represents the flow of a fluid around the stagnation regions near a solid exterior in which the fluid has no motion, and its velocity reaches zero. It is argued that heat transfer, mass deposition, pressure, and other parameters are at their highest rates near the stagnation point. Wang [38] studied the two-dimensional stagnation flow striking a heated vertical plane and found that for the infinite plane, the free convection flow relies on the Prandtl total and has no effect on heat transfer. In 2006, Wang [39] studied the two-dimensional or symmetrical stagnation flow on a moving container. The flow was found to be strongly dependent on the slip factor, and the drag decreases with the inverse of the slip factor. In addition, a rise in the slip factor and the Prandtl inflated the heat transfer and diminished the heat slip. Bachok et al. [40]investigated a nanofluid with a continuous three-dimensional stagnation point flow. They also looked at the NP volume percentage impact and the velocities ratio gradient on flow and heat transfer features. Demir and Baris [41] studied the three-dimensional stagnation-point flow of a dense impermeable fluid into a moving vertical container, as well as the injection-suction mechanism’s effect over velocity, wall shear stress, temperature, as well as heat transfer. Jamludin et al. [42] investigated the stagnation flow and heat transfer on a porous stretching/shrinking container when it was exposed to the heat source/sink impacts and a magnetic area.Heat transmission was shown to be higher in the bottom fluid (water) compared with the hybrid nanofluid. In another study, Khan et al. [43] dissected the flow convection of a uniform mixture of the water/Al2O3/SeO2 around the stagnation pinpoint containing a curved exterior with a radius ofRand suction ofS. The skin friction coefficient and hybrid nanofluids Nusselt number increased with an inflation of the amount of suction and engagement of the nanofluid. Annuar et al. [44] proposed mathematical answers for homogeneous-heterogeneous responses of the magnetohydrodynamic stagnation pinpoint of a hybrid water-Al2O3 nanofluid on a stretching/shrinking plate with the convection border state. The magnetic parameter deferred the separation of the boundary layer while the volume fraction of NPs accelerated the exterior boundary detachment. In another study, Annuar et al. [45] dissected the slip parameter impact on the stagnation pinpoint of the flow and heat transfer on an exponentially stretching/shrinking container with a water/aluminum/copper nanofluid numerically. They explored the effect of NP volume fraction, slip factor, and stretching/shrinking parameter on flow and heat transfer and found that the hybrid nanofluid allows higher heat transfer speeds compared to nanofluids and viscous fluids. In 2021, Kashi et al. [46] studied mathematical explanations and solidity research for a hybrid nanofluid stagnation pinpoint flow over a porous stretching/shrinking cylinder.They used Al2O3 and copper NPs along with water as a bottom fluid. Water/Al2O3/Cu nanofluid on shrinking cylinders possessed less heat transfer compared to water/Cu NPs and water/Al2O3 hybrid nanofluid. A proper hybridization of Cu and Al2O3 NPs with appropriate volumetric concentrations was found to allow a more increased heat transfer speed compared to the water/Cu nanofluid.Similarly, Kashi et al. [47] studied a nanofluid stagnation point flow with the mass and heat transfer on a moving plate with bidirectional slip velocities numerically. The results showed that the heat transfer is decreased with intensifying the anisotropic label,i.e., the distinction of two-sided slip rates and the thermophoresis factor. In contrast, the mass transfer rate increases with these two parameters. In another study, Nadeem et al. [48] investigated features of a three-dimensional stagnation pinpoint of a hybrid nanofluid on a cylinder. They discovered that the heat transfer speed in a hybrid nanofluid exists much higher compared to in a nanofluid.

Fig. 1. An illustration of physical model and coordinate system.

According to the literature review gaps, the hybrid nanofluid stagnation point flow on vertical plate has been investigated numerically. As a novelty the velocity and temperature slip condition have been applied simultaneously to the boundary condition of problem. Accordingly, to our knowledge, our investigation is the most recent endeavor to research the stagnation point flow of the nanofluid numerically.

This study investigated the convection flow of a hybrid nanofluid on a vertical heated plate (Fig. 1). The three-dimensional flow was applied to regionz≥0. Away from the field, the fluid flows around the symmetrical plane, and thex-axis forms an angle ofαwith the intensity of the gravity field. In addition, the vertical plane is located inz=0.

The governing equations for the hybrid nanofluid including the conservation of mass Eq. (1)), the three-dimensional Navier Stokes equations with the Boussinesq term (Eqs. (1)–((3)) and the energy equation (Eq. (5)) are as follow [20,49].

The nanofluid velocity in the directions ofx,yandzis shown respectively withu,vandwwhileTandT∞represent the nanofluid temperature and the ambient temperature, respectively.In addition,a(＞0)andKare the flow strength and temperature jump coefficient, whileSrepresents the slip coefficient, which relies on the flow and plate properties.

It is assumed thatTw-T∞=T0(x/L)T0exists as the bottom fluid specific temperature that isT0＞0 for the parallel flow andT0＜0 for the counterflow andT0=0 stands for pushed convection flow.In addition,Lstands as the exterior specific height.

Table 1 presents the equations of the thermo physical properties of the hybrid nanofluid. In Table 1,φ,μ,ρ,k,Cp,βand(ρCp)stand as the volume particle of solid NPs, dynamic viscosity, density, thermal conductivity, heat capacity, thermal expansion coeffi-cient, and heat capability.

Table 1 Thermophysical properties of hybrid nanofluids [16,50,51,52].

Table 2 Thermophysical properties of the nanoparticles and the base fluid [53].

To solve the equations by the fifth-order Runge-Kutta method,a proper value should be firstly defined for the infinite boundary (7 in the present study). In the relevant boundary conditions,a1,a2,a3anda4are equivalent tof′(∞)→1,h(∞)→0,ψ(∞)→0 andθ(∞)→0 whenη→∞. In addition, the criterion of convergence is considered as 10-6andΔη=0.001 is considered for the step size. The flowchart in Fig. 2 gives a better insight on how to solve nonlinear differential equations in this problem using thefifth-order Runge-Kutta method. Also, the CPU time to calculate each case is 4 min.

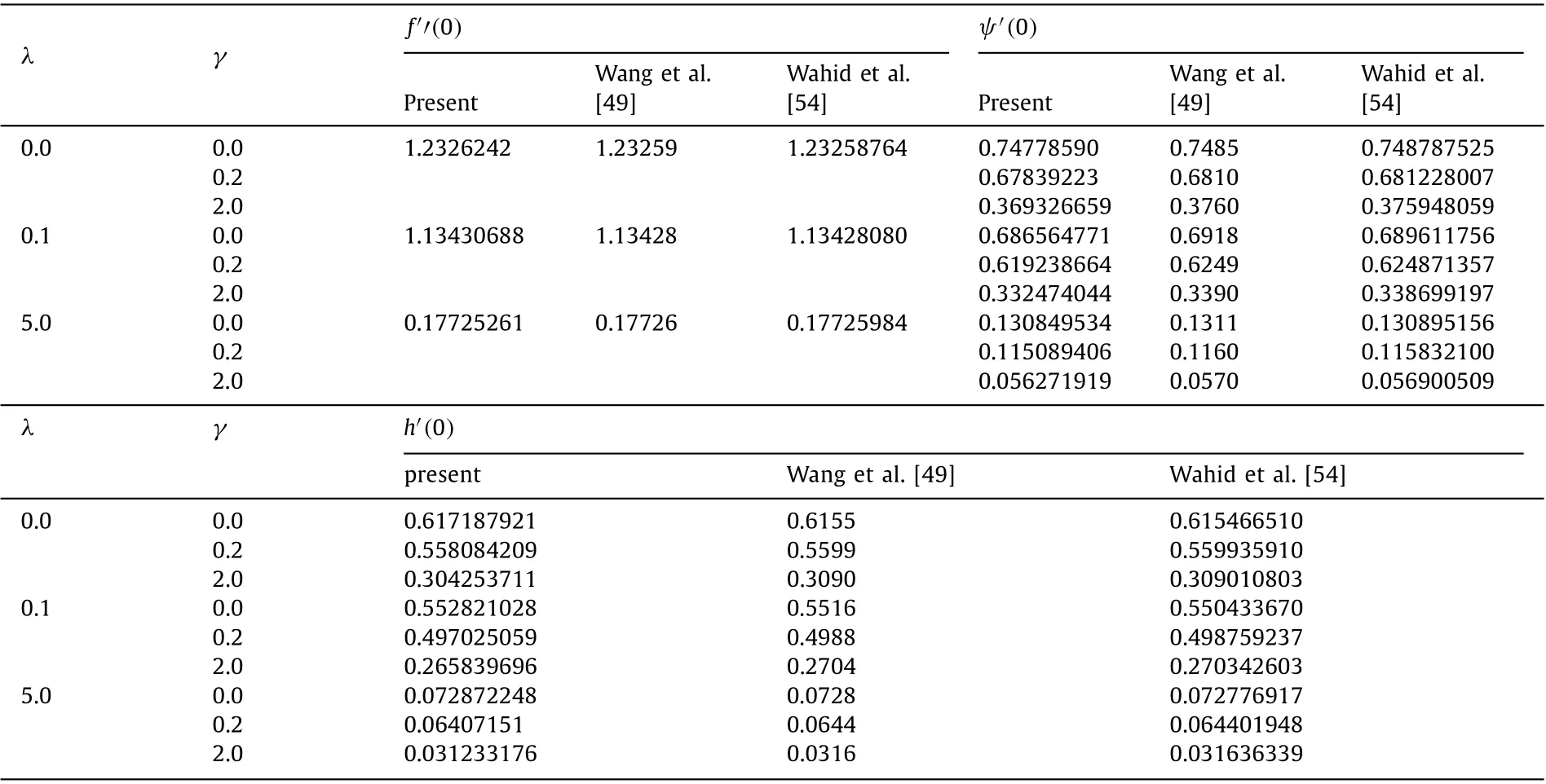
Table 3 Comparison values of f′′(0),ψ′(0) and h′(0) for an inclined stagnation flow on a vertical surface in the absence of mixed convection (φs1 =φs1 =0,fw =0 and Pr=0.7).

Fig. 2. Problem Flowchart.

This section has conducted a comparison between our results with previous studies. In Table 3, the results obtained for viscous flow without suction and the opposite flow of the convection factor are compared with results reported in Refs. [49] and [54]. As can be seen, the current investigation outcomes are well fitted with those documented in previous studies, which indicates the accuracy and application of the method used for the case under investigation.

Following validation of the calculations, this section investigates the impact of various factors over the velocity and temperature profiles. Figure 3a shows the effect of NP’s volume fraction on velocity profile(f′). As shown, on the increasing volume fraction of NPs, the velocity profile increases. Figure 3b and 3c show the effect of the volume fraction of NPs overhas well asψ. As shown,with an inflate in the volume fraction of NPs, the absolute values of thehandψ, which represent the velocity components, increase. Figure 3d shows variations in the temperature profileθ,with changes in nanoparticle volume fraction, in which on inflating volume fraction, the temperature profile increases. Therefore, a higher volume fraction of NPs is associated with a greater heating process. Figure 3e illustrates variations in the temperature gradientθ′, with changes in the volume fraction of NPs. As shown, on the increasing volume fraction of solid NPs, the absolute value of the temperature gradient increases, culminating in elevated heat transfer. Figure 4a depicts the effect of altering the velocity slip parameterλ, on variations in the velocity profile, in which an increase in slip parameter results in elevated velocities.

Fig. 3. a. Effect of volume fraction (φs2) on f′.

Fig. 4. a. Effect of velocity slip parameter(λ) on f′.

Fig. 5. a. Effect of temperature slip parameter (γ) on h.

Table 4 Numerical values of local Nusselt number (Re-1/2Nux) and skin friction coefficients (Re1/2Cfx,Re1/2Cfy) for different values of nanoparticle volume fraction (φ), velocity slip parameter(λ) and temperature slip parameter (γ).

Figure 4b and 4c illustrate the velocity slip parameter impact onhandψparameters. As the velocity slip parameter growths,the absolute value of thehandψparameters increase. Figure 4d shows relationships between variations in the temperature profileθ, and changes in the velocity slip parameter,λ. As shown, on increasing the velocity slip parameter, the temperature decreases.Thus, increasing the slip parameter results in a faster cooling process. Figure 4e displaysthe velocity slip parameter impactλ, on the temperature profile gradientθ′, in which with a rise in the velocity slip parameter, the absolute value of the temperature gradient decreases. Figure 5a depicts the impact of the temperature slip parameterγ, onh,in which growth in the temperature slip parameter decreases the absolute value ofh. Figure 5b shows the impacts of variations in the temperature slip parameterγ, onψ,in which an increase in the temperature slip parameters will raise the absolute value ofψ. In Fig. 5c, associations between changes in the temperatureθ, and temperature slip parameterγ, are shown,where on increasing the temperature slip parameter, the absolute value decreases. Figure 5d shows associations between changes in the temperature gradientθ′, and the temperature slip parameter,γ. As shown, on increasing temperature slip parameters, the absolute value of the temperature gradient decreases. Effects of temperature slip parameter, velocity slip parameter, and the volume fraction of NPs on the skin friction coefficients and Nusselt number are presented in Table 4, in which the copper volume fraction is 0.01,mixed convection parameter is -1, Prandtl number is 6.2, and Grashof numbers (Gr1,Gr2) are 1. As shown, on increasing the temperature slip parameter from 0 to3 and the volume fraction of NPs 0 to 0.02, the skin friction coefficient increases respectively 8.2%and 1% in the x-direction. On the contrary, with inflating the slip velocity parameterfrom 0 to5, thex-direction skin friction coeffi-cient diminishes 95%.Concerning the skin friction coefficient in the directiony, with increasing the velocity slip and temperature, the absolute value of they-direction skin friction coefficient declines,while an expansion in the volume fraction of NPs is associated with a raise in they-direction skin friction coefficient. According to Table 4, the Nusselt number grows 0.15% and 5.63% respectively with raising the impact of velocity parameter from 0 to 5 and volume fraction of NPs from 0 to 0.02, while, on the contrary, increasing the temperature slip parameter decreases the Nusselt number.

This study investigated the stagnation point boundary exterior flow of a three-dimensional hybrid nanofluid and heat transfer on vertically heated surfaces numerically in the existence of surface slip. Overall, the results are as follow:

·When the volume fraction of NPs boosts, the absolute value ofhandψparameters and temperature profile and gradient increases.

·On increasing the slip velocity parameter,handψand velocity are increased, while the temperature profile and temperature gradient decrease.

·With an expansion in the temperature slip parameter, the absolute value of the parameterθ′decreases, and that of the parametershandψwill increase.

·Inflation of the temperature slip parameter is connected with decreasing the Nusselt number; conversely, a rise in NP velocity and volume fraction increases the Nusselt number. Furthermore, when the volume fraction grows, the absolute value ofydirection skin friction coefficient grows, and as the temperature slip and velocity increases, the absolute value of y-direction skin friction coefficient drops.

·Thex-direction skin friction coefficient rises when the temperature slips parameter and volume percent increases. A rise in the velocity slip parameter, on the other hand, is linked to a decrease in the x-direction skin friction coefficient.

For future study, the magnetic field parameter, radiation parameter, joule heating term, and heat absorption term can be added to the governing equations.

Declaration of Competing Interest

The authors whose names are listed immediately below certify that they have no affiliations with or involvement in any organization or entity with any financial interest (such as honoraria; educational grants; participation in speakers’bureaus; membership, employment, consultancies, stock ownership, or other equity interest;and expert testimony or patent licensing arrangements), or nonfinancial interest (such as personal or professional relationships,affiliations, knowledge or beliefs) in the subject matter or materials discussed in this manuscript. The manuscript is original and it does not submit in another journal.