A machine learning based solver for pressure Poisson equations

Ruilin Chen, Xiaowei Jin,*, Hui Li,c

a Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters of the Ministry of Industry and Information Technology, Harbin Institute of Technology, Harbin 150090, China

b Key Lab of Structures Dynamic Behavior and Control of the Ministry of Education, Harbin Institute of Technology, Harbin 150090, China

c Guangdong-Hong Kong-Macao Joint Laboratory for Data-Driven Fluid Mechanics and Engineering Applications, Harbin Institute of Technology (Shenzhen),Shenzhen 518055, China

Keywords:Pressure Poisson equation Machine learning Projection method Multi-scale GNN

ABSTRACT When using the projection method (or fractional step method) to solve the incompressible Navier-Stokes equations, the projection step involves solving a large-scale pressure Poisson equation (PPE), which is computationally expensive and time-consuming. In this study, a machine learning based method is proposed to solve the large-scale PPE. An machine learning (ML)-block is used to completely or partially(if not sufficiently accurate) replace the traditional PPE iterative solver thus accelerating the solution of the incompressible Navier-Stokes equations. The ML-block is designed as a multi-scale graph neural network (GNN) framework, in which the original high-resolution graph corresponds to the discrete grids of the solution domain, graphs with the same resolution are connected by graph convolution operation, and graphs with different resolutions are connected by down/up prolongation operation. The well trained MLblock will act as a general-purpose PPE solver for a certain kind of flow problems. The proposed method is verified via solving two-dimensional Kolmogorov flows (Re = 1000 and Re = 5000) with different source terms. On the premise of achieving a specified high precision (ML-block partially replaces the traditional iterative solver), the ML-block provides a better initial iteration value for the traditional iterative solver, which greatly reduces the number of iterations of the traditional iterative solver and speeds up the solution of the PPE. Numerical experiments show that the ML-block has great advantages in accelerating the solving of the Navier-Stokes equations while ensuring high accuracy.

The Navier-Stokes equations are nonlinear partial differential equations (PDEs) describing viscous fluid flow, which are applicable to various scientific and engineering flow problems, such as river flow, air flow around wings, ocean currents, blood flow in the human cardiovascular system, etc. The solution of the Navier-Stokes equations is of great significance in the field of fluid mechanics. The convection term leads to the high nonlinearity of Navier-Stokes equations, and the solutions contain multi-scale flow structures. Nowadays, the numerical method is still a workhorse tool for solving complex flow phenomena. Thanks to the rapid growth of computer computing power and speed, the computational fluid dynamics (CFD) has made great progress [1–4]. For incompressible Navier-Stokes equations, the main difficulty of numerical solution lies in the treatment of pressure, that is, how to deal with the coupling between velocity and pressure under incompressible constraints. To overcome this difficulty, Chorin[5] proposed the projection method (or fractional step method),which is widely used for its skillfully decoupling of the velocity and pressure fields. In the projection method, an incomplete form of momentum equations is first solved to obtain an intermediate velocity field, which is usually not divergence-free, then the velocity field is projected into the divergence-free field without changing the vorticity. This projection step is achieved by solving the pressure Poisson equation (PPE) and is usually more timeconsuming and computationally expensive than other steps in the overall solution process.

The PPE can be transformed into a large-scale system of linear algebraic equations with numerical discretization. For complex flow problems, sufficiently fine discretization is required to capture the multi-scale flow structures. In the case of turbulent flow,for example, the required discretization grid to capture its smallest scale eddy is proportional toRe9/4, whereReis the Reynolds number, and the magnitude ofReencountered in engineering is often very large. It is intolerable to solve large-scale discrete PPE by inverse operation directly, and there are various alternative iterative methods for solving this equation, such as Jacobi method, Gauss-Seidel (GS) method, successive over relaxation (SOR) method, algebraic multigrid (AMG) method and conjugate gradient / preconditioned conjugate gradient (CG/PCG) method, etc. [6–11]. Jacobi,GS and SOR methods are stationary iterative methods, which are simple to understand and implement but slow to converge, while AMG, CG and PCG are nonstationary iterative methods, which are relatively harder to understand and implement but higher efficient.Jacobi, SOR and AMG are also commonly used as preconditioners of PCG for higher efficiency. Although these iterative methods avoid explicitly computing the inverse of large sparse matrices,their convergence is limited by the spectral properties (spectral radius or spectral condition number) of iterative matrix and initial iteration error, and their entire iterative process must be repeated at each solution time step, which is time-consuming. It is crucial to provide a better preconditioner (in order to obtain an iterative matrix with more favorable spectral properties) and initial iterative value to improve the effectiveness of the iterative methods.

There is a consensus that new efficient and accurate methods are urgently needed to solve the aforementioned large-scale PPE problems. In recent years, machine learning (ML) techniques have made significant progress in the scientific field [12–16], as they provide powerful methods for analyzing large amounts of highdimensional data and building complex models. In particular, there has been some work on using ML to replace or accelerate the iterative methods used in some fluid simulations. Yang et al. [17] proposed a data-driven projection method that that avoids iterative computation using an artificial neural network (ANN), which takes known local features on a discrete grid as input and outputs corresponding pressure predictions. Since it is purely data-driven at some discrete grid points, it is hard to guarantee the divergencefree condition over the entire field. Tompson et al. [18] used a convolutional network (CNN) with a highly tailored architecture to solve the linear system derived from incompressible Euler equations using splitting method. However, their method cannot guarantee to find an exact solution to the pressure projection step, and their method is better than Jacobi method in running time and accuracy, but cannot reach the precision of PCG. Obiols-Sales et al.[19] introduced a coupled physics simulation and deep learning framework for accelerating the convergence of Reynolds-averaged Navier-Stokes simulations. Luz et al. [20] proposed a graph neural network framework (GNN) for learning AMG prolongation operators for linear systems, which has some success in improving the AMG convergence rate, but it still cannot guide how to select the optimal coarse-approximation framework, as AMG itself has many parameters that need to be selected based on experience. Li and Farimani [21] proposed a data-driven graph neural networks model for fluid simulation under Lagrangian representation, in which fluid particles are represented as nodes and their interactions are represented as edges. Compared to classical simulation methods, their model is more computationally efficient because it operates on a smaller neighborhood, but their model suffers from the bottleneck of going through two rounds of neighborhood search, which takes more time than other models. Kochkov et al. [22] used end-to-end deep learning (DL) to improve the approximation inside CFD for simulating two-dimensional turbulence, i.e. solving the equations on coarse grids and using ML based interpolate differential operators to compensate for the loss of accuracy. Özbay et al. [23] constructed a Poisson CNN to infer the solution of the Poisson equation on a 2D Cartesian grid with different resolutions given the right-hand side term, arbitrary boundary conditions, and grid parameters. The mean prediction error of their model on the test cases is less than 10%, have an improvement compared to the first step of traditional iterative methods, while it does not make much sense only compared to the first-step results of traditional iterative methods as the advantage of traditional iterative methods is the ability to converge to a specified accuracy for downstream tasks. Xiao et al. [24] presented a CNN-based Poisson solver to improve simulation speed and extrapolation ability in Eulerian fluid simulation, which can rapidly produce simulation results that are visually similar to the results from traditional iterative methods, but cannot produce results exactly the same as traditional iterative methods. Although the above works attempt to use ML models to speed up some fluid simulations, a practical problem is that the accuracy of ML models cannot achieve the high precision of traditional iterative methods. ML models have the advantage of being able to approximate physical models quickly but at the cost of accuracy. The accuracy of ML models may be suffi-cient for some simple flow problems (such as the Euler flow mentioned above) or just prediction problems, but it is difficult to meet the turbulent flow problems that require high accuracy. Moreover,ML models will inevitably lose a certain accuracy on non-training dataset. All these factors can lead to the solving process unstable, as obtaining high precision solutions is crucial for downstream solving tasks. Therefore, in the process of participating in equations solving, ML models should not only pursue the improvement of the solving speed, but also ensure the stable and the accuracy of solving method.

In this study, we develop a machine learning-based solver for the large-scale PPE split from the Navier-Stokes equations using projection method. We use an ML-block (multi-scale GNN) to completely or partially (if not sufficiently accurate) replace the traditional PPE iterative solver to accelerate the solution of the incompressible Navier-Stokes equations. The well trained ML-block will act as a general-purpose PPE solver for a certain kind of flow problems. When the pressure solution output by the ML-block does not meet a specified high accuracy, it is taken as the initial iteration value of the traditional iterative solver. It ensures that the ML-block can long-term stably participate in solving the Navier-Stokes equations. We verify the framework on the problem of solving two-dimensional Kolmogorov flows (Re= 1000 andRe= 5000)with different source terms. The results show that the proposed method has great advantages in accelerating the solving of the Navier-Stokes equations while ensuring high accuracy.

The incompressible Navier-Stokes equations are as follows:

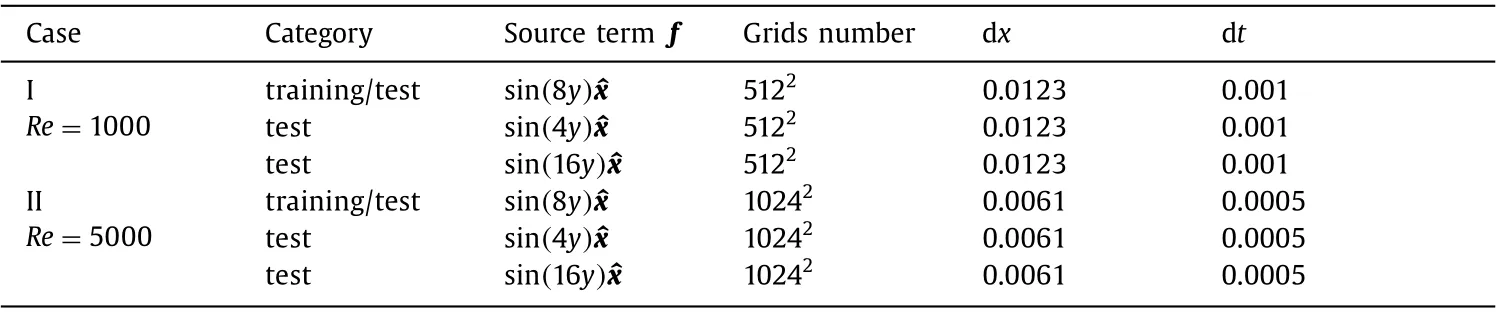
Table 1 Some basic solution settings (dimensionless).

where superscriptnrepresents the solution time step, C represents convective discrete terms, L represents viscous discrete terms, G is the discrete gradient operator, and D is the discrete divergence operator. The details of the operators mentiond above can be found in literature [27]. Eq. (3) is called "prediction step", that is, an intermediate velocityu*is obtained by solving the momentum equations ignoring the effect of the pressure term, which cannot be guaranteed to be divergence-free. Eqs. (4) and (5) are called "projection step", which are used to project the intermediate velocity into a divergence-free space, i.e., the intermediate velocity is modified by a PPE (Eq. (4)) so that it satisfies the incompressibility condition.

The discrete PPE (Eq. (4)) can be rewritten in large-scale matrix-vector form:

In order to avoid or minimize the long iterative process of the above iterative methods, we design an ML-block to completely or partially replace the traditional iterative solver to accelerate the solution of the Navier-Stokes equations, as shown in Fig. 1. Figure 1a shows the numerical solution framework of the Navier-Stokes equations embedded with an ML-block (secondorder explicit-implicit temporal discretization scheme). The MLblock performs only one forward computation at each time step,which is non-iterative. It should be noted that the ML-block is applicable to the numerical solution framework with other temporal discretization schemes, because the projection operations Eqs. (4) and ((5)) are basically consistent in different temporal discretization schemes. A PCG iterator (a most commonly used iterative method for solving large-scale sparse linear systems) is added after the ML-block, i.e., the pressure field output by the ML-block is used as the initial iteration value of the PCG (denoted as MLblock + PCG), so as to obtain a specified high precision pressure field and ensure long-term stable calculation. Note that the PCG iterator is no longer involved if the pressure field output by the ML-block already meets the specified accuracy requirements.

Inspired by the work of Lino et al. [28], the ML-block is designed as a multi-scale GNN as shown in Fig. 1b, where the input is the intermediate velocity divergence ∇·u*and the output is the pressurep,G1his the original high-resolution graph, its edges express the connection relation of discrete grids in the solution domain,G2h,G3handG4hare the low-resolution graph of level-2,level-3 and level-4, respectively. The graph convolution operation[29] is defined as:

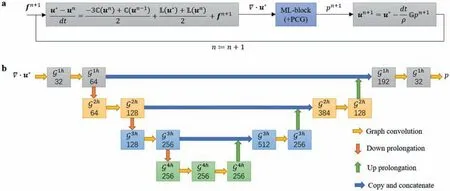
Fig. 1. a Numerical solution framework for the Navier-Stokes equations embedded with an ML-block (second-order explicit-implicit temporal discretization scheme). b MLblock (multi-scale GNN), G1h is the original high-resolution graph, G2h, G3h and G4h are the low-resolution graph of level-2, level-3 and level-4, respectively, and the number represents the number of neurons in the corresponding layer.

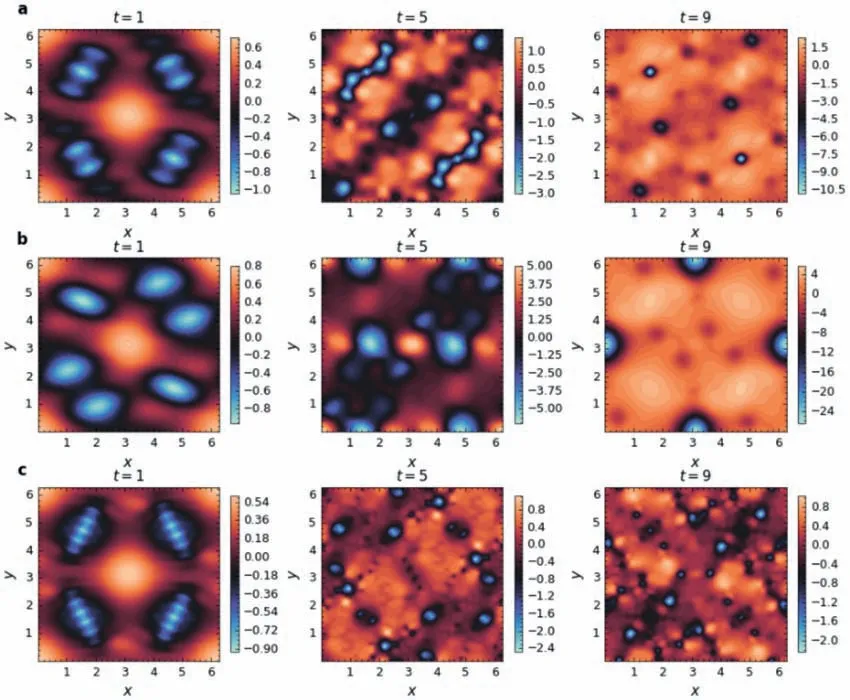
Fig. 2. Several pressure field solution snapshots of Kolmogorov flow at Re=1000 using ML-block+PCG method, a f =sin(8y)ˆx, b f =sin(4y)ˆx,c, f =sin(16y)ˆx.

where the first term is the supervised pressure field matching error loss, the second term is the unsupervised divergence loss(to satisfy the incompressibility constraint), the third term is the network weight decay regularization with weight decay coeffi-cientλθ, and ‖·‖2represents the Euclidean norm of a vector.The ML-block is trained using AdamW [31] optimizer to minimize the loss function. After the ML-block is well trained, it will be used as a general-purpose PPE solver for a certain kind of flow problems.

Then we discuss the solution of two-dimensional Kolmogorov flow [32] with periodic boundary conditions in [0, 2πL] × [0, 2πL]and forcingf=sin(ky)ˆx(i.e., the source term in Eq. (1),kis the

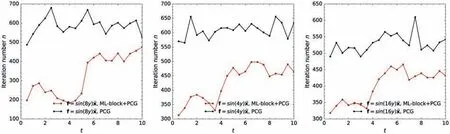
Fig. 3. Iteration numbers of ML-block + PCG and PCG for Kolmogorov flow with Re=1000 when the solution accuracy of ‖App-b‖2 ≤1×10-5 is achieved.

Fig. 4. Several pressure field solution snapshots of Kolmogorov flow at Re=5000 using ML-block+PCG method, a f =sin(8y)ˆx, b f =sin(4y)ˆx, c f =sin(16y)ˆx.

The flow field gradually develops from laminar flow to turbulent flow. The solution domain is discretized using a fully conservative higher-order finite difference scheme [33], and some basic solution settings are shown in Table 1.

We first train the ML-block with the dataset from Kolmogorov flow withRe=1000 andf=sin(8y)ˆx, which contains 1500 highfidelity field snapshots withint=[0,5]. After completing the MLblock training, to verify its applicability and effectiveness, let the ML-block participate in solving Kolmogorov flows with different source terms (see Table 1) according to the framework shown in Fig. 1a. Several pressure field solution snapshots of Kolmogorov flow atRe=1000 using ML-block+PCG method are as shown in Fig. 2. Here, ML-block +PCG refers to taking the pressure field output by ML-block as the initial iteration value of PCG, while PCG refers to taking the pressure field solution of the previous time step as the initial iteration value of PCG. For uniform comparison, the termination iteration conditions of ML-block +PCG and PCG are set to achieve the same specified high solution accuracy,i.e., to ensure that the same high-precision solution is obtained.Figure 3 shows the comparison of the iteration numbers of MLblock + PCG and PCG when the solution accuracy of ‖App-b‖2≤1×10-5is achieved. As can be seen from Fig. 3, the participation of ML-block greatly reduces the number of iterations of PCG. Note that fewer iterations indicate lower solution times and faster solution speed, which is true on any device. Furthermore, since the forward computation of ML-Block is non-iterative, its time consumption is almost negligible compared to hundreds or thousands of iterative computations.

The following acceleration coefficient is defined to evaluate the degree of acceleration of ML-block for accelerating PCG:

where,nPCGandnML-block+PCGrepresent the number of iterations for PCG and ML-block +PCG to achieve the same solution accuracy, respectively. Eq. (15) is the ratio of the reduced (or increased)iteration number of ML-block + PCG compared with PCG to the iteration number of ML-block +PCG, which intuitively reflects the percentage of speed increase (or decrease) of ML-block +PCG compared with PCG. The acceleration coefficients corresponding to Fig. 3 are shown in Table 2. It can be seen that in the training set (Re=1000,f=sin(8y)ˆx,t=[0,5]), the solution speed of MLblock + PCG is nearly 3 times (ξ+1) that of PCG, and in other cases, ML-block + PCG still maintains a speed improvement of 0.1-0.7 over PCG. The performance of ML-block + PCG in the test set is indeed inferior to that in the training set, but its solution speed still has a certain improvement than PCG. It indicates that the ML-block provides a better initial iteration value (closer to the exact pressure field solution) for PCG, and the ML-block maintains a certain long-term robustness for Kolmogorov flows with different source terms. Although the ML-block suffers from some over-fitting issues, it does show great advantages in accelerating the solution of the Navier-Stokes equations.

Then we retrain the ML-block with the dataset (contains 1500 high-fidelity field snapshots withint=[0,5]) from Kolmogorov flow withRe=5000 andf=sin(8y)ˆx. Figure 4 shows several pressure field solution snapshots of Kolmogorov flow atRe=5000 using ML-block+PCG method, and similar to what is expressed in Figs. 3, 5 shows the comparison of the iteration numbers of MLblock + PCG and PCG. It can be seen that the performance of MLblock + PCG is still far superior to that of PCG, and the reduction of the iteration numbers of PCG by using ML-block is considerable. According to Table 2, the solution speed of ML-block + PCG is nearly 2 times that of PCG in the training set (Re=5000,f=sin(8y)ˆx,t=[0,5]), and it maintains a speed improvement of 0.1-0.8 over PCG in other cases. Therefore, the participation of ML-block does play a role in accelerating the solution of PPE,which is of great significance for the solution of large-scale systems. We also give the acceleration coefficients by Eq. (15) when‖App-b‖2≤1×10-4and ‖App-b‖2≤1×10-6in Tables A1 and A2 in the Appendix. It can be seen that when the solution accuracy is changed to 1×10-4, the acceleration coefficient increases,and when the solution accuracy is changed to 1×10-6, the acceleration coefficient decreases. This makes sense, as the proportion of ML-block participation increases when the solution accuracy requirements decrease, and vice versa.

According to the above numerical experimental results and Eq. (8), the well trained ML-block adaptively provides PCG with a more suitable initial iteration value, thus greatly reducing the number of iterations. It has certain guiding significance in accelerating CFD calculation based on machine learning. For example, according to the framework shown in Fig. 1a, a better ML-block can be designed or a more suitable training dataset can be selected. In addition, according to Eq. (8), machine learning models can also be used to explore a more suitable preconditioner.

In this study, we propose an ML-based solver for the largescale PPE split from the Navier-Stokes equations using projection method. In this framework, an ML-block (multi-scale GNN) is used to completely or partially (if not sufficiently accurate) replace the traditional PPE iterative solver to accelerate the solution of the incompressible Navier-Stokes equations. The speed-up performance of the ML-block is verified via solving two-dimensional Kolmogorov flows (Re= 1000 and 5000) with different source terms.The results demonstrated that the participation of the well-trained ML-block significantly reduces the number of iterations for the traditional PCG solver to reach the specified accuracy, i.e., the MLblock provides a better initial iteration value for the PCG solver. It indicates that the participation of ML-block does play a role in accelerating the solution of the Navier-Stokes equations. Embeddingan ML-block into the numerical solution framework of the Navier-Stokes equations is a good starting point, and we will continue to investigate how to design a more general and speedier ML-block in the future.

Table A1 Acceleration coefficients for Kolmogorov flow at Re=1000.

Table A2 Acceleration coefficients for Kolmogorov flow at Re=5000.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

This research was funded by the National Natural Science Foundation of China (Grant No. 52108452), the Science Fund for Creative Research Groups of the National Natural Science Foundation of China (Grant No. 51921006), and the Guangdong Science and Technology Department (Grant No. 2020B1212030001).

Appendix