非简谐振动对石墨烯量子电容和热稳定性的影响

吴 强，高君华，2，周虹君，郑瑞伦

(1.重庆文理学院重庆市高校新型储能器件及应用工程研究中心，重庆 402160;2.黑龙江大学 电子工程学院，哈尔滨 150080)

1 引 言

自1987 年Luryi 提出量子电容的概念和2008年石墨烯制备成功以来［1］，人们已对石墨烯材料的量子电容进行了不少研究.John 等人［2］对二维电子气的量子电容进行了计算，Fang 等人［3］对单层石墨烯、Guo 等人［4］对石墨烯纳米带、Kliros［5］，Cheremisn［6］，Alisultanov 等人［7］对双层石墨烯、Trabelsi［8］对在SiC 上的外延石墨烯分别与对应材料的量子电容进行了研究.Bhahcharya 等人［9］还对具有曲折边界的单层和石墨烯纳米带的量子电容进行估计，Xia 等人［10］对如何精确测量量子电容问题开展实验研究.2015 年杨光敏等［11］使用密度泛函理论的第一性原理，采用VASP 软件包，在广义梯度近似下，对N 掺杂石墨烯的量子电容进行研究并分析量子电容提升储能的原因.但这些研究未反映出温度等对量子电容的影响，更未研究量子电容的热稳定性问题.2020 年Davydov［12］对石墨烯纳米结构的量子电容从模型上给以予测，得到石墨烯纳米结构量子电容变化规律的解析式.该文虽提到量子电容随温度变化，但研究中认为原子静止，未考虑到原子的非简谐振动，体现不出原子相互作用对量子电容的影响，而且也未研究它的热稳定性问题.

石墨烯材料具有完美的晶体结构和独特的电学、光学、热学、力学等性能，在电子器件、能量储存、环境科学等领域具有广泛的应用前景.它的突出应用之一是制作超级电容器.在实际应用中，多变的外场以及多变的高温环境，原子非简谐振动效应突出，不仅使石墨烯材料的性质随温度发生变化，而且使材料发生形变，影响材料的性能稳定性和超级电容器的使用寿命.考虑到原子振动非简谐效应，确定石墨烯材料量子电容随温度、外电场等的变化规律及其热稳定性，这对于石墨烯材料在超级电容器等储能器件上的应用就是一个亟待解决的重要问题.为此，本文将应用固体物理理论和方法，对此问题进行研究，以期对提高超级电容器储能性能问题提供理论参考.

2 物理模型

我们研究的石墨烯是由N 个碳原子构成的二维六角格子平面系统，设平面为OXY 平面，Z 轴垂直向上，坐标系选取如图1 所示.一个原子的平均原子相互作用能为［13］:

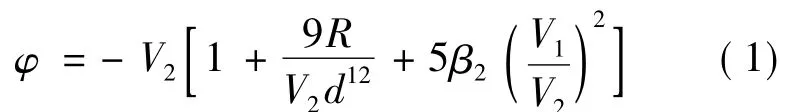
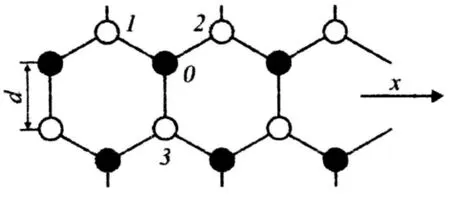
图1 石墨烯的结构示意图Fig.1 Schematic diagram of the structure of graphene

其中，V2为两原子的sp2轨道σ 键的共价能，它与原子间距离d 的平方成反比:这里的m 为自由电子的质量; V1为金属化能，R=0.154 ×104( ħ2/2m)，a0为玻尔半径，β2是与维数有关的参量，β2=2/3.

原子在平衡位置附近作非简谐振动，将原子相互作用能φ( d) 在平衡位置d0附近展开，偏离δ=d - d0很小时，有

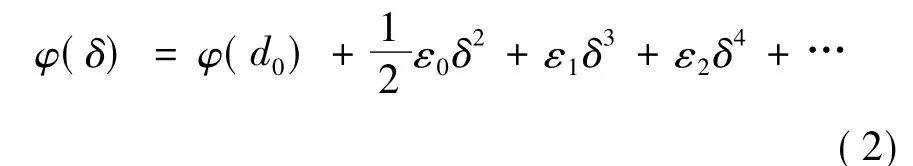
其中，ε0、ε1、ε2分别是简谐系数、第一和第二非简谐系数.其具体表示式见文献［14］所述.

3 石墨烯量子电容随温度和电压的变化

John 等人［2］给出电荷密度与电子态密度的关系为:

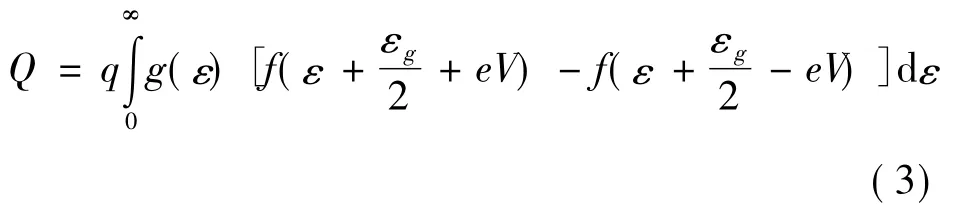
其中，g( ε) 为电子的态密度，它与一个原子上的平均态密度ρ( ε) 的关系为ρ( ε)=g( ε) /N，f( ε) 为费米分布函数，εg为禁带宽度.将( 3) 式代入量子电容CQ的定义式，即单位质量( 或单位面积) 材料因量子效应产生电荷量改变dQ 对电势差dV 的比值:

对单层石墨烯，禁带宽度εg=0 ，求得石墨烯量子电容随温度和电压的变化为［15］:

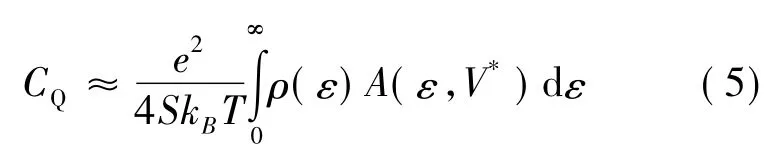
这里，

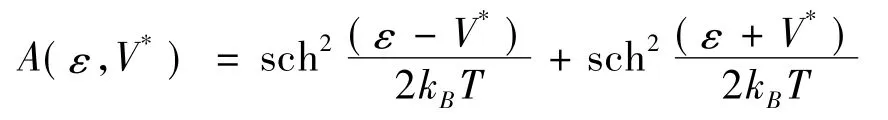
而ρ( ε) 为一个原子上的平均态密度，V*=eV，V是外电场电势; S 是一个表面原子所占面积，对于石墨烯，为晶格常数.按照文献［13］，单层石墨烯的态密度为:

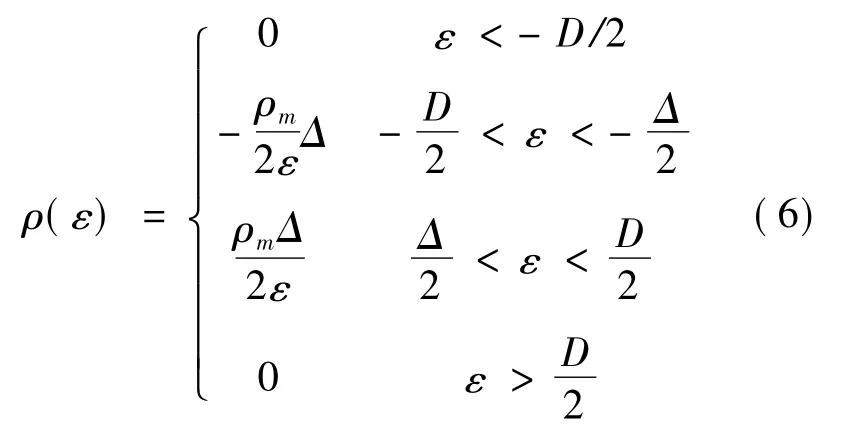
将(6) 式代入(5) 式，并令τ=t/2kBT，ν*=eV/2kBT，得到不考虑原子非简谐振动时的量子电容为［15］:

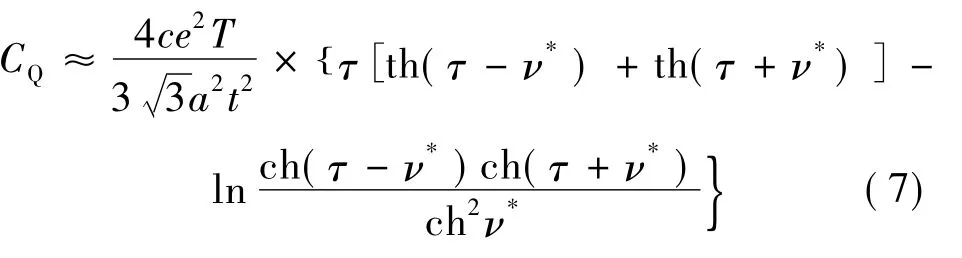
其中，c=2/(1 +2ln3) ，而t 是最近邻格点的交换能.

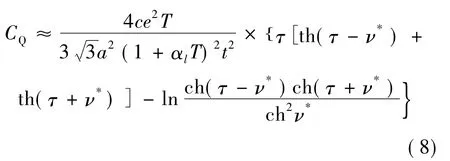
其中，线膨帐系数为［16］:

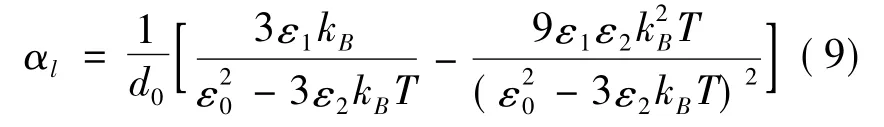
这里的d0为绝对零度时最近邻原子间的距离.

4 石墨烯量子电容的热稳定性随温度的变化

材料在热、电、光、化学等内外因素作用下，性能逐渐降低，甚至完全丧失使用价值，这种现象叫材料的老化( Ageing).除材料老化以及材料掺杂、缺陷等会影响石墨烯蓄热传热和储能性能的稳定性外，温度无疑是另一重要因素.原子的非简谐振动，温度的变化引起膨胀或收缩，使原子组成结构和相互作用发生变化，导致一个原子所占面积以及电荷密度电子态发生改变，进而引起量子电容等蓄能性能发生改变.

热稳定性常用温度稳定性( Temperature stability) 系数来描述，它反应了物理量随温度的波动情况［17］.为了描述石墨烯量子电容的温度稳定性，普遍采用它的温度系数表示: 设系统的性能参数为f，热稳定系数定义为αf=(1/f) ( df/dT).αf愈小，热性能愈稳定.按此定义，量子电容热稳定性系数定义为:

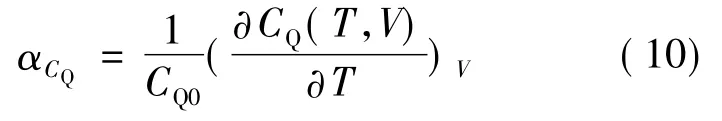
其中，CQ0为T 趋于0 K，V=congst 时的量子电容，按文献［15］，可取CQ0=1.6 μF·cm-2.将(8) 、(9) 式代入( 10) 式，得到石墨烯量子电容随温度和电压变化的具体表示.

5 原子非谐振动对石墨烯量子电容及热稳定性变化规律的影响

5.1 石墨烯材料量子电容随温度的变化规律

Davydov［13］给出石墨烯零温时键长d0=1.42×10-10m，将文献［13］的数据代入(1) 式，求得简谐系数ε0=3.5388 ×102J·m-2，第一非简谐系数ε1=-3.49725 ×1012J·m-3，第二非简谐系数ε2=3.20140 ×1022J·m-4.代入(9) 式，得到线膨胀系数αl随温度的变化.

最近邻格点间的交换能t=3 eV，晶格常数a=1.42 ×10-10m，将玻尔兹曼常数、电子电荷等一起代入( 8) 式，求得不同电压下理想单层石墨烯材料的量子电容( 单位: F·m-2) 随温度的变化，如图2 所示.其中V=0.1 V 时的部分数据如表1 所示.图中的曲线0、1、2 和表1 中的0、1、2 分别是简谐近似、计算第一非简谐项、同时计算第一、二非简谐项的结果.

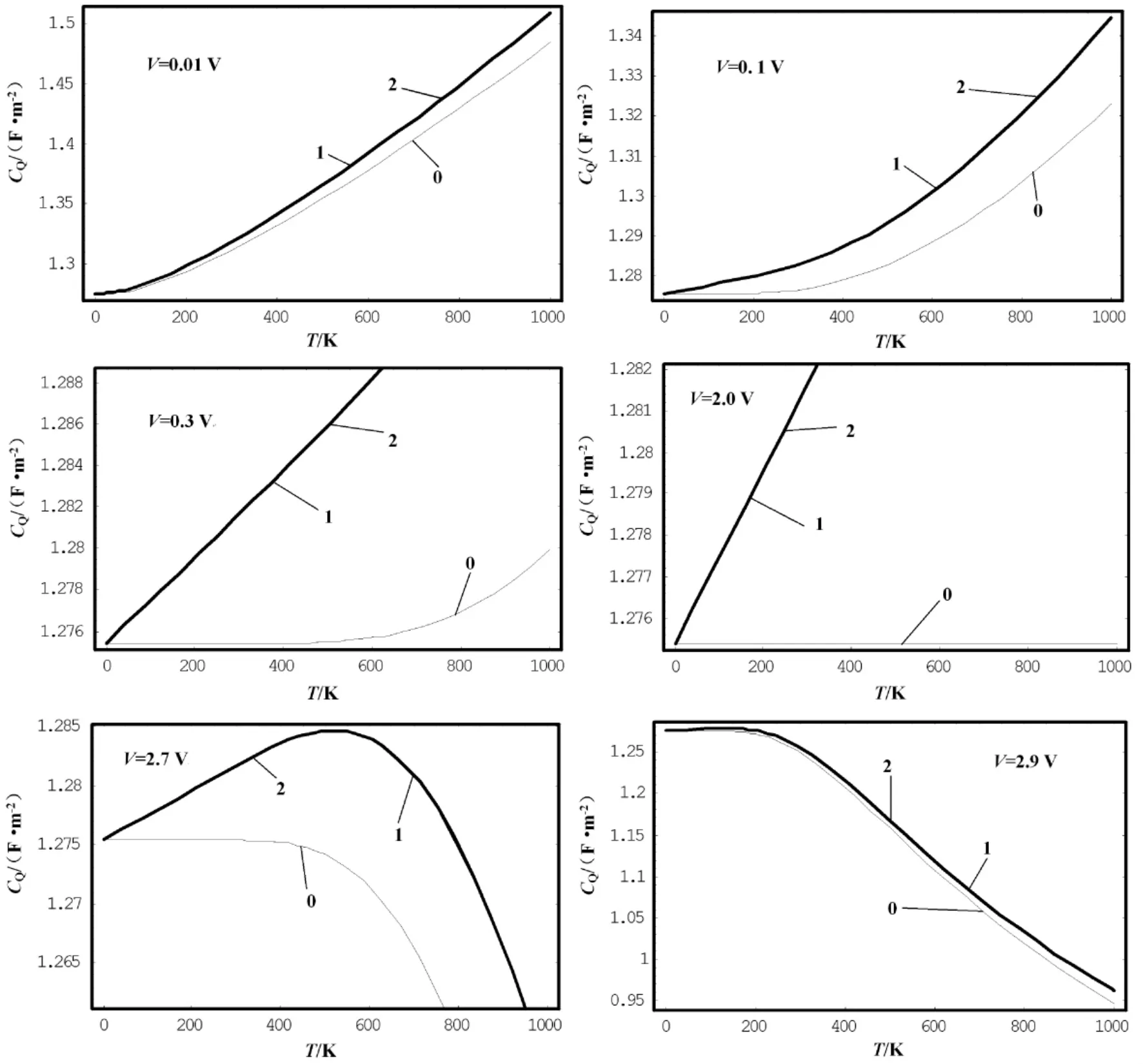
图2 不同电压下单层石墨烯材料量子电容随温度的变化Fig.2 Changes of the quantum capacitance of a single -layer graphene material with temperature under different voltages

由图2 和表1 可以看出，( 1) 电压一定的条件下，单层石墨烯量子电容随温度升高发生非线性变化，具体变化情况与电压有关，电压小于2.3 V 时，量子电容随温度升高而增大; 而电压高于2.3 V 时，量子电容先随温度升高而增大，到达某一温度值时，反而随温度升高而减小.(2) 非简谐项对量子电容随温度的变化规律有重要影响.与简谐近似相比，考虑到原子非简谐振动后的量子电容的值有所增大，且温度愈高，两者的差愈大，即非简谐效应愈显著.例如，当温度为300 K 时，非简谐情况的量子电容值比简谐近似时的值大0.33%; 而当温度为1 000 K 时，后者比前者大1.47%.( 3) 本文的计算结果不仅在数量级上与文献［10］的结果( 0.23 F·m-2)接近，而且给出了量子电容随温度的变化规律.

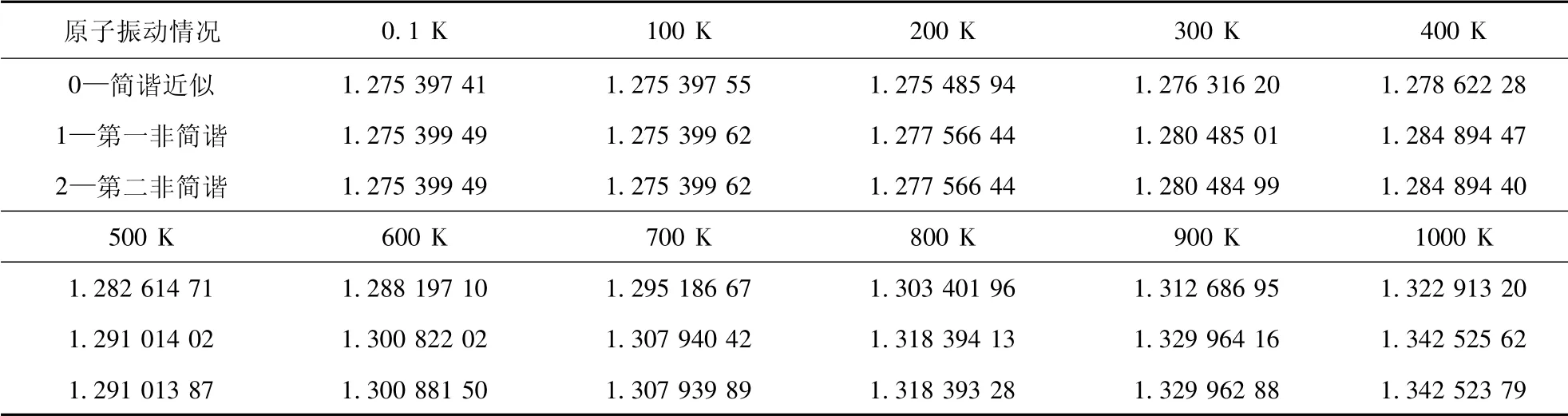
表1 当V=0.1 V 时，简谐、第一非简谐、第二非简谐量子电容随温度变化的对比Table 1 Comparison of the changes of simple harmonic，first anharmonic，and second anharmonic quantum capacitances CQ( F·m -2) with temperature at V=0.1 V ( CQ单位: F·m -2)

5.2 石墨烯材料量子电容随电压的变化规律

将数据代入(8) 式和( 9) 式，得到温度为T=300 K 和T=800 K 情况下，石墨烯量子电容CQ随电压V 的变化，如图3 所示，部分数据如表2 所示.图3 的曲线0、1、2 的含义同图2.

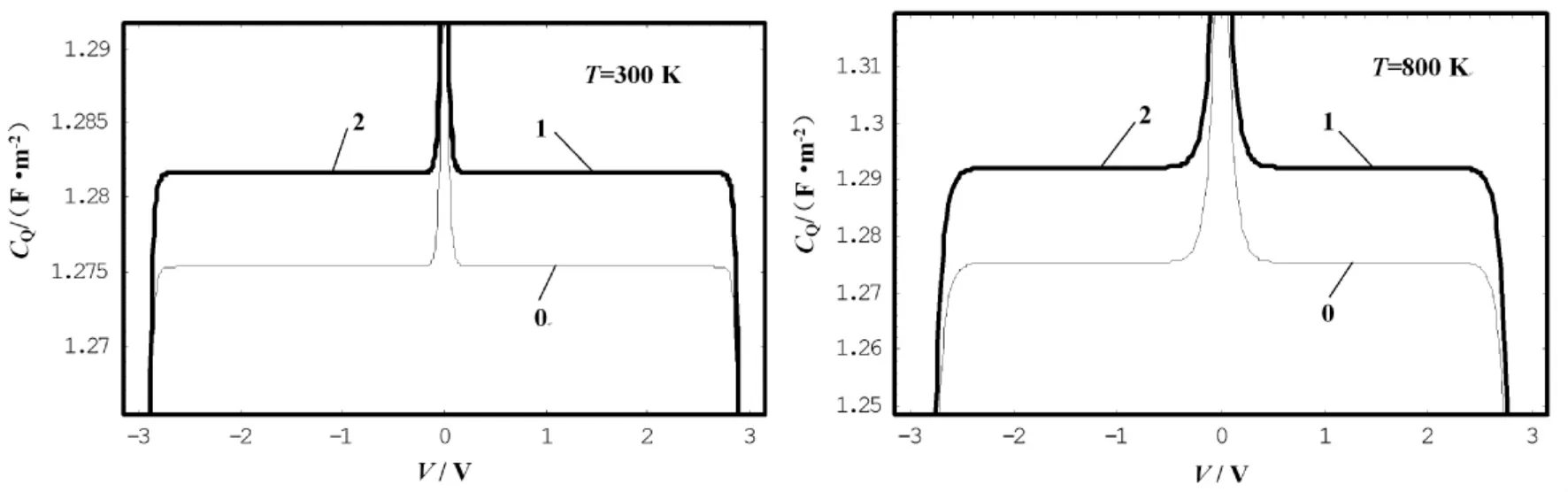
图3 不同温度下单层石墨烯量子比电容随电压的变化Fig.3 Changes of graphene quantum capacitance with voltage at different temperatures

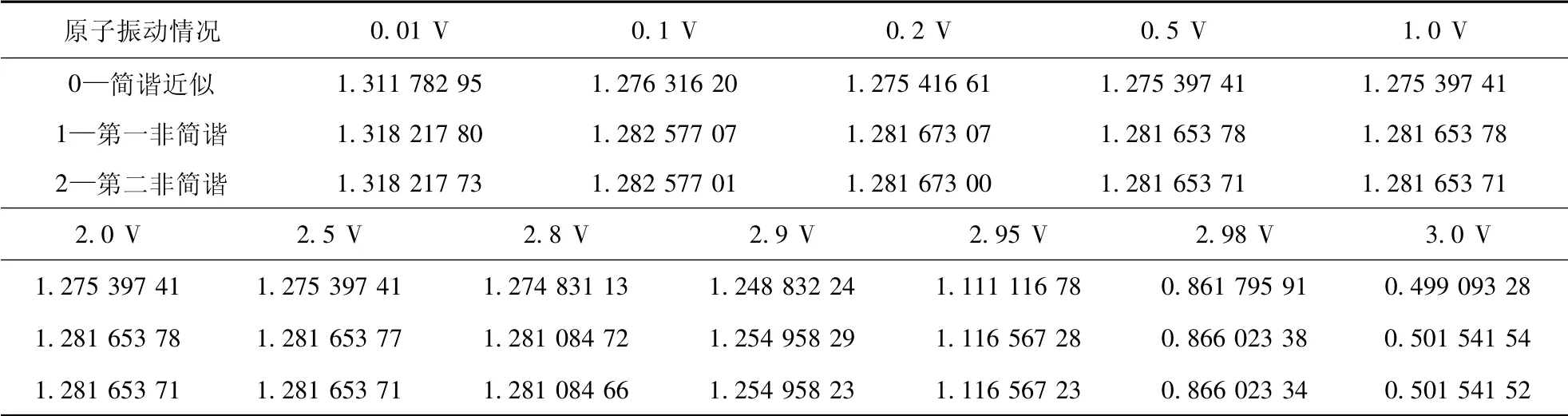
表2 当T=300 K 时，简谐(0) 、第一非谐(1) 、第二非谐(2) 量子比电容随电压的变化Table 2 Changes of graphene quantum capacitance CQ( F·m -2) with voltage at T=300 K( CQ单位: F·m -2)

由图2 和表1 可以看出，( 1) 给定温度下，石墨烯量子电容随电压的增大产生非线性变化，其中，当电压值小于0.4 V 时，量子电容由极大值迅速减小，当电压值在0.4 ～2.8 V 时，量子电容较大几乎保持不变; 当电压值大于2.8 V 时，量子电容迅速减小; 电压值大于3 V 时，量子电容变为0.(2) 与简谐情况的值相比，非简谐情况的量子电容值有所增大( 由1.275 F·m-2增大到1.282 F·m-2) ，但曲线的变化趋势相同，其中，温度较高时的曲线其变化趋势较缓慢，曲线较圆滑.

5.3 石墨烯量子电容的热稳定性的变化规律

将上述数据代入(8) 式和(9) 式，再代入(10)式，就得到不同电压情况下，石墨烯量子电容的温度稳定性系数随温度的变化，如图4 所示.图4 的曲线0、1、2 的含义同图2.其中V=0.1 V时简谐0、第一非简谐1、第二非简谐2 的部分数据如表3 所示.

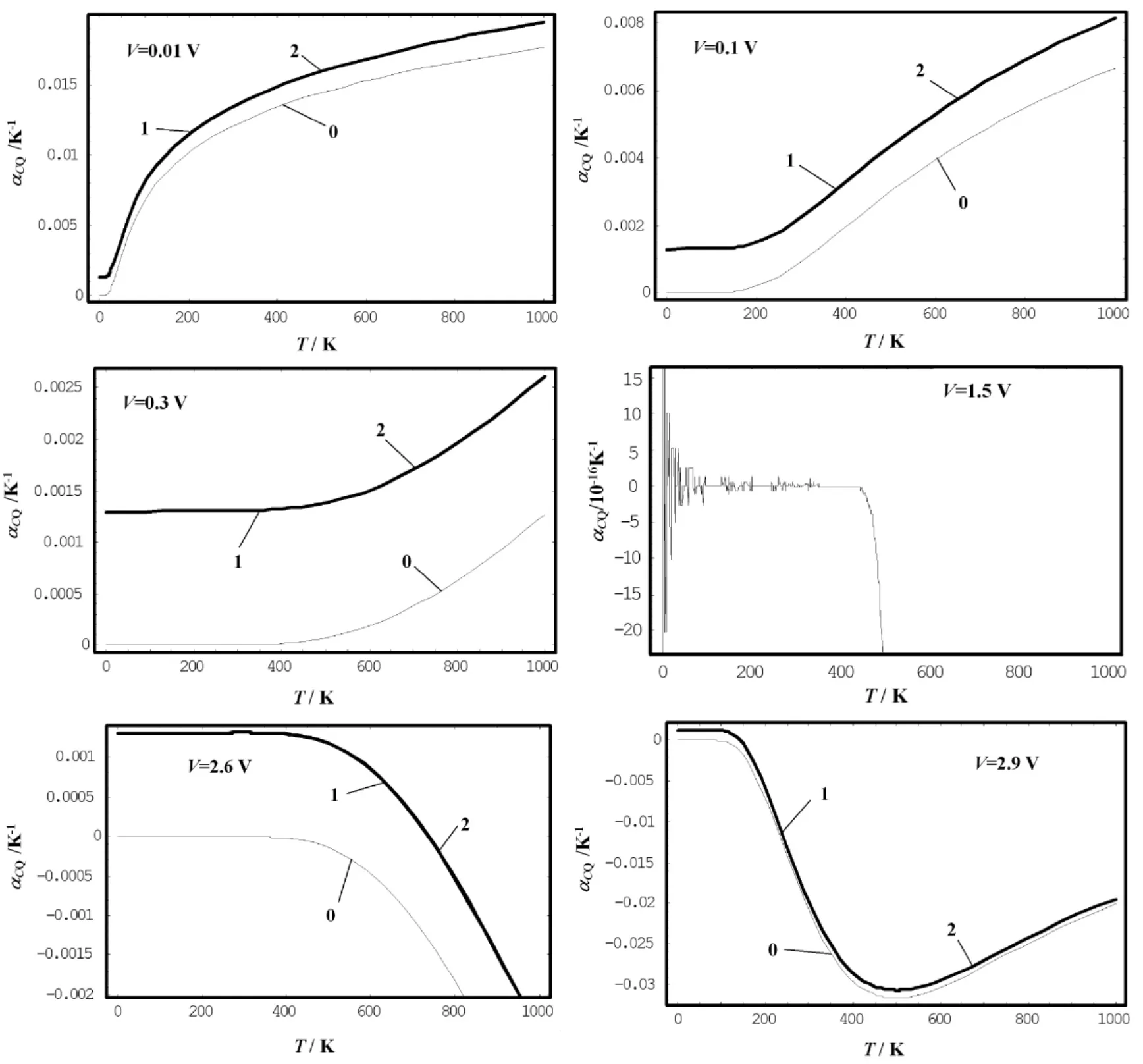
图4 不同电压条件下石墨烯量子电容的温度稳定性系数随温度的变化Fig.4 Variations of temperature stability coefficient of graphene quantum capacitor with temperature under different voltage conditions

由图4 和表3 可看出，( 1) 石墨烯量子电容的温度稳定性系数随温度升高发生非线性变化，具体变化情况与电压有关.其中，当电压小于1.5 V 时，其温度稳定性系数随温度升高而由缓慢变化到很快增大; 当电压大于1.8 V 时，则随温度升高而由缓慢变化到很快减小; 当电压在1.5 ～1.8 V 之间时，变化曲线逐渐发生反向变化; (2) 在电压在1.5 ～1.8 V 之间，而温度低于800 K 的情况下，石墨烯量子电容的温度稳定性系数最小且不随温度而变，这表明在此电压和温度范围内，石墨烯量子电容的温度稳定性最好;(3) 与简谐近似的值相比，考虑到非简谐项后，石墨烯量子电容热稳定性系数有所增大，且增大的情况与温度有关.例如，在电压为0.1 V 的条件下，温度为400 K 时，非简谐情况的量子电容热稳定性系数值比简谐近似的值大67.47 %; 而温度为1 000 K 时，则大22.36%.这表明非简谐效应会使石墨烯量子电容热稳定性比简谐近似情况变差，即非简谐效应具有降低量子电容热稳定性的作用.

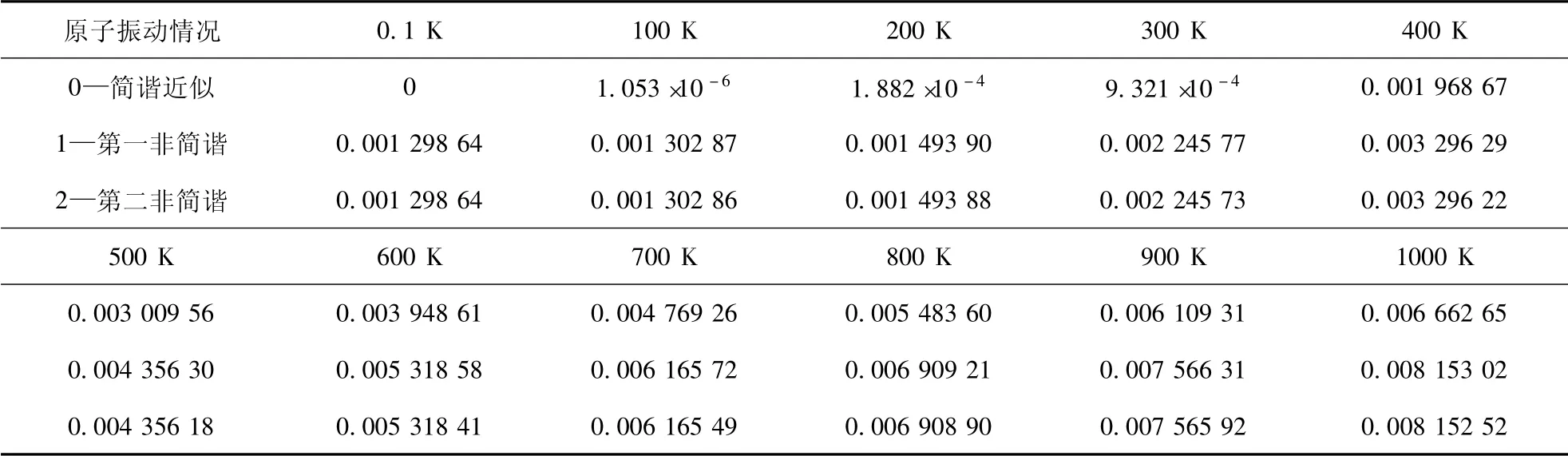
表3 当V=0.1 V 时，不同情况的量子比电容热稳定性系数αC Q随温度的变化Table 3 Changes of thermal stability coefficient αC Q ( K -1) of graphene quantum capacitance with temperature at V=0.1 V( 单位: K -1)

6 结 论

本文的研究给出了石墨烯材料量子电容及其热稳定性的变化规律，发现都与温度和电压有关，具体结果由(8) 式、(9) 式、(10) 式表示.具体描述为:

(1) 当电压一定时，石墨烯量子电容和它的温度稳定性系数均随随温度升高发生非线性变化，变化情况与电压有关.其中，当电压小于2.3 V时，量子电容随温度升高而增大，它的温度稳定性系数随温度升高由缓慢变化到很快增大; 而电压高于2.3 V 时，量子电容先随温度升高而增大，到达某一温度值时，随温度升高而减小，它的温度稳定性系数随温度升高而由缓慢变化到很快减小; 而当温度一定时，量子电容只在电压值为0.4 ～2.8 V 范围内才变化较小，而电压值大于2.8 V 时，量子电容迅速减小并趋于0.

(2) 与简谐近似情况相比，非简谐项会使石墨烯量子比电容有所增大，且温度愈高，两者的差愈大，即非简谐效应愈大.例如，当温度为300 K 时，非简谐振动情况的量子比电容值比简谐近似的值大0.33%; 而温度为1 000 K 时，则非简谐情况大1.47%.

(3) 与简谐近似的值相比，非简谐项会使石墨烯量子比电容热稳定性系数有所增大，其中温度为400 K 时，非简谐情况的热稳定性系数值比简谐近似的值大67.47%，而温度为1 000 K 时，则非简谐情况大22.36%.非简谐效应会使石墨烯量子电容热稳定性比简谐情况变差，即非简谐效应会降低量子电容热稳定性的作用.

(4) 电压在1.5 ～1.8 V 之间，而温度低于800 K 的情况下，石墨烯量子电容的温度稳定性系数最小且不随温度而变，此时石墨烯量子电容的温度稳定性最好.

本文所得有关量子电容的结果不仅与已有文献的结果接近，而且还给出了量子电容和它的温度稳定性系数随温度的变化规律，这对石墨烯在超级电容器储能性能上的应用是有参考价值的.