井下履带式探测机器人及其运动抗扰控制研究

单杰， 关丙火

(国家能源集团 神东煤炭集团公司， 陕西 神木 719315)

0 引言

当前，中国煤矿安全形势依然严峻，煤矿事故死亡人数是世界上其他产煤国家煤矿事故死亡总数的2～3倍[1-3]。井下灾害发生后，救援的最大困难在于原有通信瘫痪、工作通道坍塌堵塞，导致无法进行信息和物质交换。由于不能掌握井下灾害情况，地面工作人员很难进行决策并精准施救[4-5]。井下探测机器人可提前布置于井下或从地面释放至井下进行探测作业，通过轮式或履带式移动底盘驱动，并携带各类探测仪器，不仅可实时探测井下现场环境参数并回传，还可用于应急通信甚至灾后辅助救援[6-8]。由于井下尤其是灾后路面环境极其复杂，多为非结构路面，所以对机器人的结构设计、爬坡越障性能及动力驱动算法等提出较高要求[9-10]。

在机器人结构设计方面，为提升机器人灾后爬坡越障能力，通常采用履带式移动平台。履带式移动底盘具有较好的移动越障能力，并且能够原地零半径转向，更适应井下复杂的非结构路面环境[11-12]。但与轮式底盘相比，履带式底盘体积和质量更大，导致其移动和转向时受到较大路面摩擦力作用，故对驱动机构的驱动性能和控制精度提出更高要求。尤其当履带式移动机器人在井下进行高精度定点探测或救援作业时，对移动转向机构的驱动性能和控制精度提出很高要求。

在机器人驱动控制方面，永磁同步电动机(Permanent Magnet Synchronous Motor，PMSM)因具有结构简单、效率高、功率密度大等优势而被广泛应用于井下履带式机器人动力驱动系统[13]。但井下探测机器人作业环境复杂，驱动电动机需要有较宽的转速调节范围，同时，因机器人携带多种探测或救援装备且需进行爬坡越障，易导致负载扰动，具有较强的非线性和不确定性。此外，PMSM本身是多变量、强耦合的非线性系统，目前常规的基于误差的比例积分微分(Proportional Integral Derivative, PID)控制器很难满足控制需求[14]。

针对上述难题，本文设计了一种四摆臂井下履带式探测机器人，分析了机器人运动工况和爬坡越障参数。在此基础上，针对机器人PMSM，速度环采用自抗扰控制器(Active Disturbance Rejection Control，ADRC)，电流环采用比例积分(Proportional Integral，PI)控制器，采用磁场定向控制(Field-Oriented Control，FOC)技术对PMSM进行驱动，从而提升机器人在井下作业时的响应性能和抗干扰性能。

1 井下履带式探测机器人移动平台设计

1.1 机器人整机结构

井下履带式探测机器人主要包括履带式移动平台、摆臂机构、驱动机构、探测系统、通信系统等，如图1所示。

1—履带式移动平台；2—摆臂机构；3—驱动机构； 4—探测系统；5—通信系统。图1 井下履带式探测机器人样机Fig.1 Prototype of underground crawler detection robot

履带式移动平台为探测机器人的移动载体，内部设置有动力驱动机构、电源和控制器等，外部两侧安装有悬挂组件，用以带动机器人移动。为进一步提升机器人攀爬性能，在本体前后两侧设计四摆臂机构进行辅助越障。摆臂机构由内部电动机驱动进行角度调整。探测系统根据现场实际侦查需求搭载不同的传感组件。通信系统实现机器人与地面指挥站间的信息交互功能。

1.2 摆臂和动力驱动机构设计

机器人移动采用PMSM驱动，左右各设置1组PMSM，通过减速箱进行减速，以提升转矩。机器人前后摆臂采用外摆臂结构，内部采用齿轮传动，包括前摆臂、移动组件、后摆臂、动力驱动机构、摆臂驱动机构，如图2所示。摆臂减速箱将摆臂驱动电动机的动力源降速增矩后传送至摆臂组件上。通过摆臂驱动电动机转动，带动前后摆臂进行角度调整，实现机器人辅助越障爬坡。

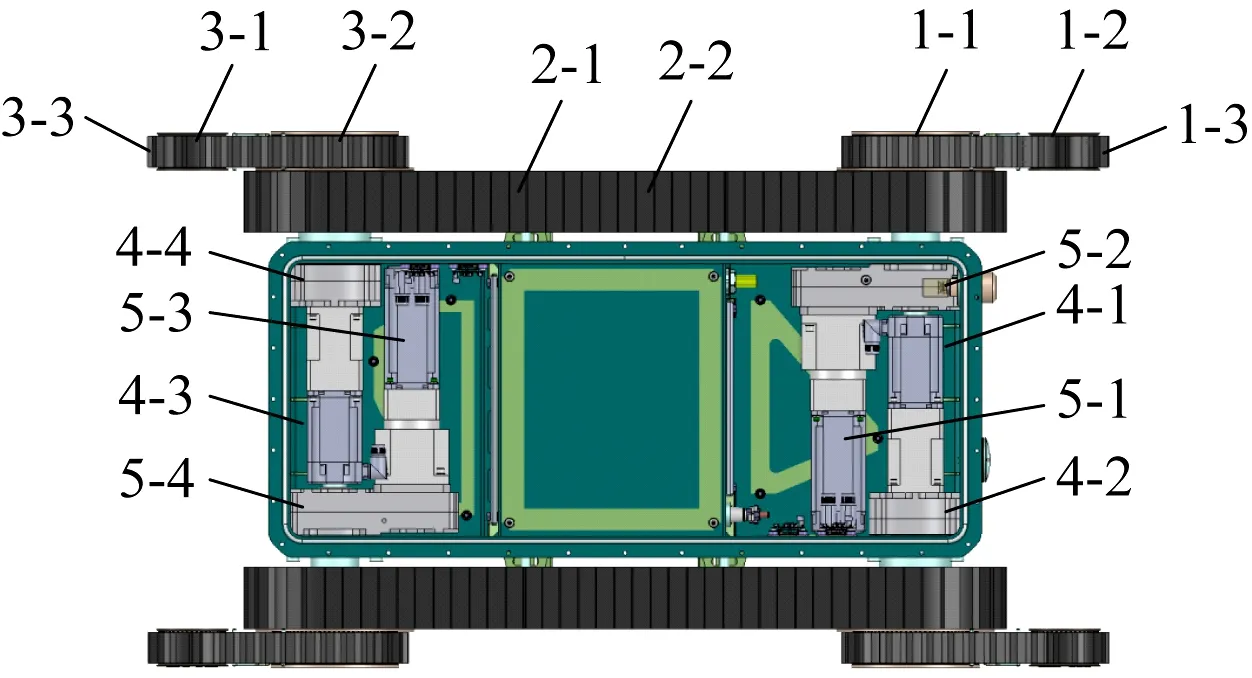
1-1—前摆臂驱动轮；1-2—前摆臂从动轮；1-3—前摆臂履带； 2-1—承重轮；2-2—移动履带；3-1—后摆臂驱动轮； 3-2—后摆臂从动轮;3-3—后摆臂履带；4-1—右驱动电动机； 4-2—右驱动减速箱；4-3—左驱动电动机；4-4—左驱动减速箱； 5-1—前摆臂驱动电动机；5-2—前摆臂减速箱； 5-3—后摆臂驱动电动机；5-4—后摆臂减速箱。图2 机器人摆臂和动力驱动机构Fig.2 Robot swing and movement arm drive mechanism

1.3 机器人越障分析

机器人运动工况一般包括平地行驶和爬坡越障。在井下实施探测救援时，机器人应具备强悍的爬坡越障性能，而影响其爬坡越障性能的重要因素之一是机器人的质心位置分布。井下履带式探测机器人摆臂及本体质心情况如图3所示。

图3 机器人摆臂及本体质心分布Fig.3 Robot swing arm and body centroid distribution

XbObYb为惯性坐标系，X0O0Y0为本体坐标系，X1O1Y1为前摆臂坐标系，X2O2Y2为后摆臂坐标系;CM，Cf，Cr分别为机器人的本体质心、前后摆臂质心。机器人关键机械参数见表1。

根据质心变换方程和质心运动学方程[15]，可计算出本文井下履带式探测机器人最大爬坡倾角为38°，最大越障高度为359 mm。

根据移动底盘机械特性，建立如下典型工况。工况1：平地直行；工况2：直行爬坡，坡度为38°。机器人在移动过程中受内外部阻力作用。机器人两侧履带接地压力为

(1)

式中：pmin，pmax分别为最小和最大接地压力；m为载荷质量；bw为履带宽度；lw为履带接地长度；ew为机器人本体质心CM相对于本体中心线的纵向偏心距。

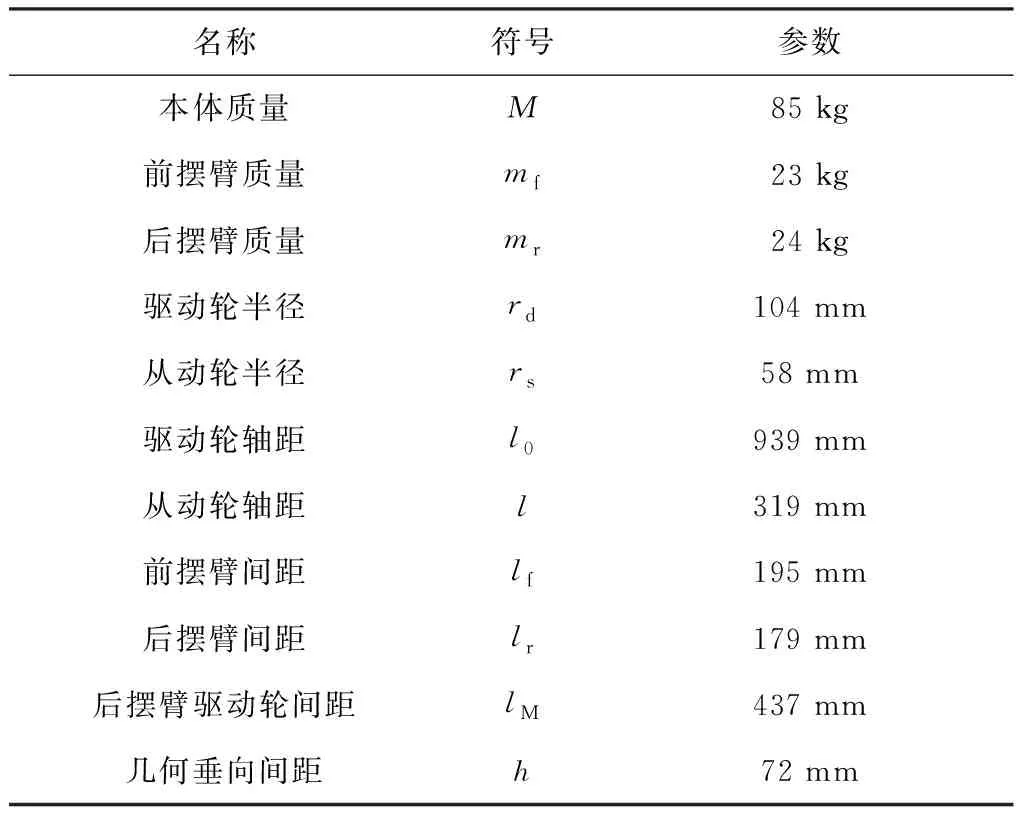
表1 机器人关键机械参数Table 1 The key mechanical parameters of the robot

对于机器人履带系统与驱动轮、从动轮及承重轮等轮系的内部阻力Fin，计算时取摩擦因数μ=0.3。履带系统与路面的外部阻力为

(2)

式中：n,K分别为路面土壤变形指数和模量；paver为平均接地压力，paver∈[pmin,pmax]；cw为机器人本体质心CM相对于本体中心线的横向偏心距;sw为履带的轨距。

根据上述参数和实际路面环境，考虑动力输出减速机的减速比及效率问题，上述2种工况下，探测机器人左右PMSM转矩和转速见表2。可看出，当机器人爬坡时转矩需求较平地直行时要高。

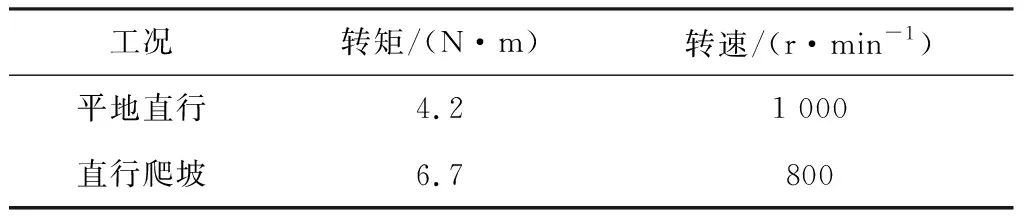
表2 机器人2种工况下PMSM转矩和转速Table 2 PMSM torque and rotational speed under two working conditions of the robot

2 PMSM抗扰控制方案

对PMSM进行建模分析，设计速度环和电流环控制器；同时，为实现PMSM精准转速控制，还需对PMSM内部参数进行解耦控制。

2.1 PMSM数学模型

考虑定子电流d轴分量id=0的矢量控制策略，采用三相正弦波电流驱动的隐极子式PMSM，其状态方程为

(3)

式中：iq为定子电流q轴分量；ω为角速度；Rs为定子电阻；Li为电动机电感;Ld,Lq为电感d,q轴分量,Ld=Lq=Li；ψf为转子磁链；Pn为电动机极对数；J为转子转动惯量；Q为阻尼系数;ud，uq分别为定子电压d，q轴分量；TL为负载转矩。

2.2 ADRC结构及数学模型

由于探测机器人携带大量观测仪器且在复杂非结构路面环境运动，各类干扰对PMSM的扰动明显，容易造成机器人轨迹跟踪和运动精度差。为提高机器人的运动精度和抗干扰能力，本文采用ADRC对PMSM进行控制[16]。

ADRC最先是为解决常规PID控制器的缺陷而提出[17]，包括跟踪微分器(Tracking Differentiator，TD)、扩张状态观测器(Extended State Observer，ESO)及非线性状态误差反馈(Nonlinear State Error Feedback，NLSEF)3个部分，如图4所示。将ADRC内部的不确定扰动和外部干扰定义为广义总扰动，利用ESO进行扰动观测，并利用NLSEF进行扰动补偿，从而实现对总扰动的抑制。

图4 ADRC结构Fig.4 ADRC structure

为方便描述ADRC模型，以一阶被控对象为例阐述其抗扰原理：

(4)

式中：x，U，y分别为状态变量、控制输入、控制输出；f(x,w)为系统未知扰动；w为扰动状态变量；B为输入增益。

ADRC对应的TD，NLSEF和ESO模型分别为[17]

(5)

(6)

(7)

式中：E0，E1和E2为观测误差；z11为期望输出的跟踪信号；ydesire为期望输出；z为状态变量；v为速度因子；fal(·)为非线性函数[16-17]；α0,α1,α2,δ0,δ1,δ2为fal(·)控制参数；z21，z22为ESO的状态变量，z22/B用于补偿被控对象内外总扰动；β1为NLSEF增益；U0(t)为NLSEF的输出控制信号；t为时间;β01，β02为ESO增益。

2.3 速度环ADRC设计

PMSM转速控制直接决定探测机器人的空间位置及机器人能否快速精准跟踪目标轨迹。

将式(3)改写为ADRC的标准型：

Qω/J-TL/J+iqPnψf/J

(8)

为提高系统响应性能，采用直接误差函数代替非线性函数fal(·)，重新设计后的NLSEF和ESO模型分别为

(9)

(10)

式中：ka为ADRC增益；Ndesire为期望转速；E=z21-ω。

可以看到，此时ESO变为标准的线性观测器，故可进行极点配置，其特征方程稳定的充要条件是β01>0,β02>0。

2.4 电流环PI控制器设计

由于探测机器人采用id=0的控制策略，所以采用PI控制器就能很好地调节d轴电流。由式(3)可知，定子电流id和iq在d，q轴上产生耦合电动势，此时对id，iq进行解耦，可得解耦后定子电压d，q轴分量ud0，uq0：

(11)

式中ωe为PMSM电角速度。

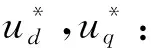
(12)

根据电动机的电流环带宽γ与时间常数τ的关系：τ=min{Ld/Rs,Lq/Rs}，γ=2π/τ，推算出如下关系：kpd=γLd,kid=γRs,kpq=γLq,kiq=γRs。

2.5 FOC原理

采用FOC方法[18-19]实现对转矩的精准控制。FOC的本质是对电流进行实时采样并进行电流/电压坐标变换，实现空间矢量脉宽调制(Space Vector Pulse Width Modulation，SVPWM)。在进行SVPWM时，需判断电压空间矢量所在扇区，确定本开关周期所使用的基本电压空间矢量，具体原理和步骤见文献[19]。

3 PMSM抗扰控制仿真分析

3.1 Simulink仿真建模

对PMSM进行仿真实验，将本文PMSM控制方案与常规的双PI控制方案进行对比，双PI控制方案即速度环和电流环均采用PI控制器(PI+PI)。速度环采用ADRC、电流环采用PI控制器(ADRC+PI)的Simulink仿真模型架构如图5所示。

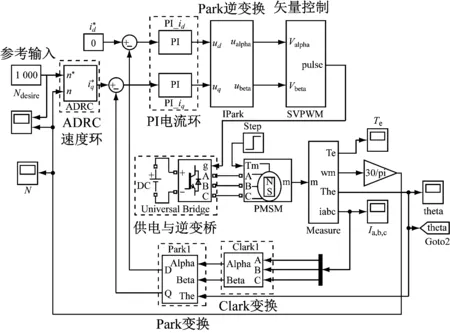
图5 采用ADRC+PI方案时PMSM Simulink 仿真模型架构Fig.5 Simulink simulation model architecture of PMSM when ADRC+PI scheme is adopted

采用双PI控制方案的Simulink仿真模型架构如图6所示。

3.2 平地直行工况仿真

在平地直行工况下，机器人左右两侧的PMSM转矩为32 N·m，期望转速Ndesire=1 000 r/min，定子电阻Rs=0.08 Ω，Li=Ld=Lq=6.5×10-2H，电动机极对数Pn=4，转子转动惯量J=1.2×10-3kg·m2，转子磁链ψf=0.143 Wb。当电动机进入平稳期后，持续转矩为4.2 N·m，在t=0.2 s时引入2 N·m干扰量。

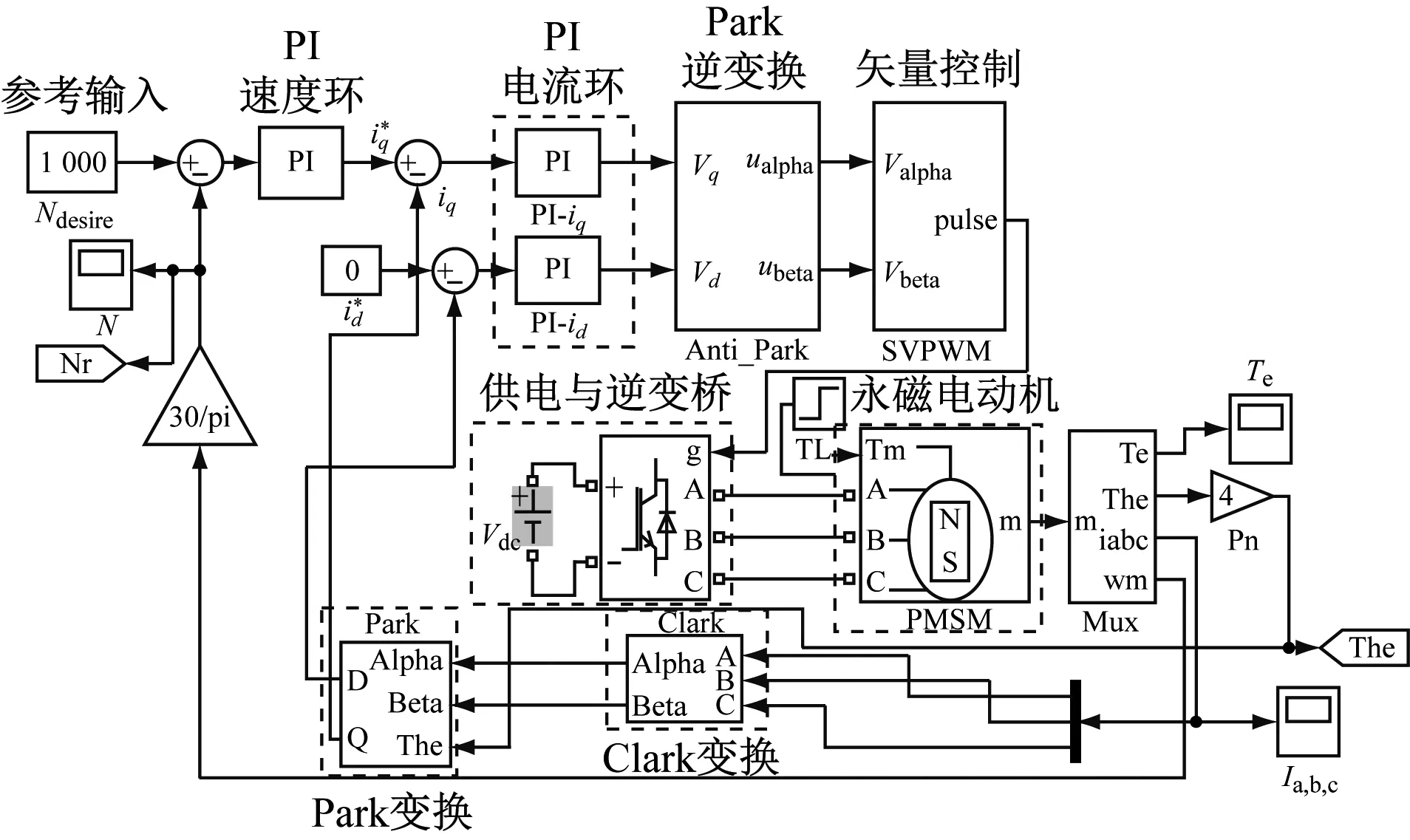
图6 采用PI+PI方案时PMSM Simulink 仿真模型架构Fig.6 Simulink simulation model architecture of PMSM when PI+PI scheme is adopted

平地直行工况下PMSM转速N响应曲线如图7所示。在PMSM启动阶段，速度环采用ADRC时基本没有超调，而采用PI控制器时超调很明显，最大超调量超过8%；速度环采用ADRC时调节时间仅为0.04 s，而采用PI控制器时调节时间超过0.1 s。在0.2 s加入扰动后，采用PI控制器时PMSM摄动变化明显，转速摄动幅度超过20 r/min，而采用ADRC时PMSM转速非常稳定，抗干扰能力较强。

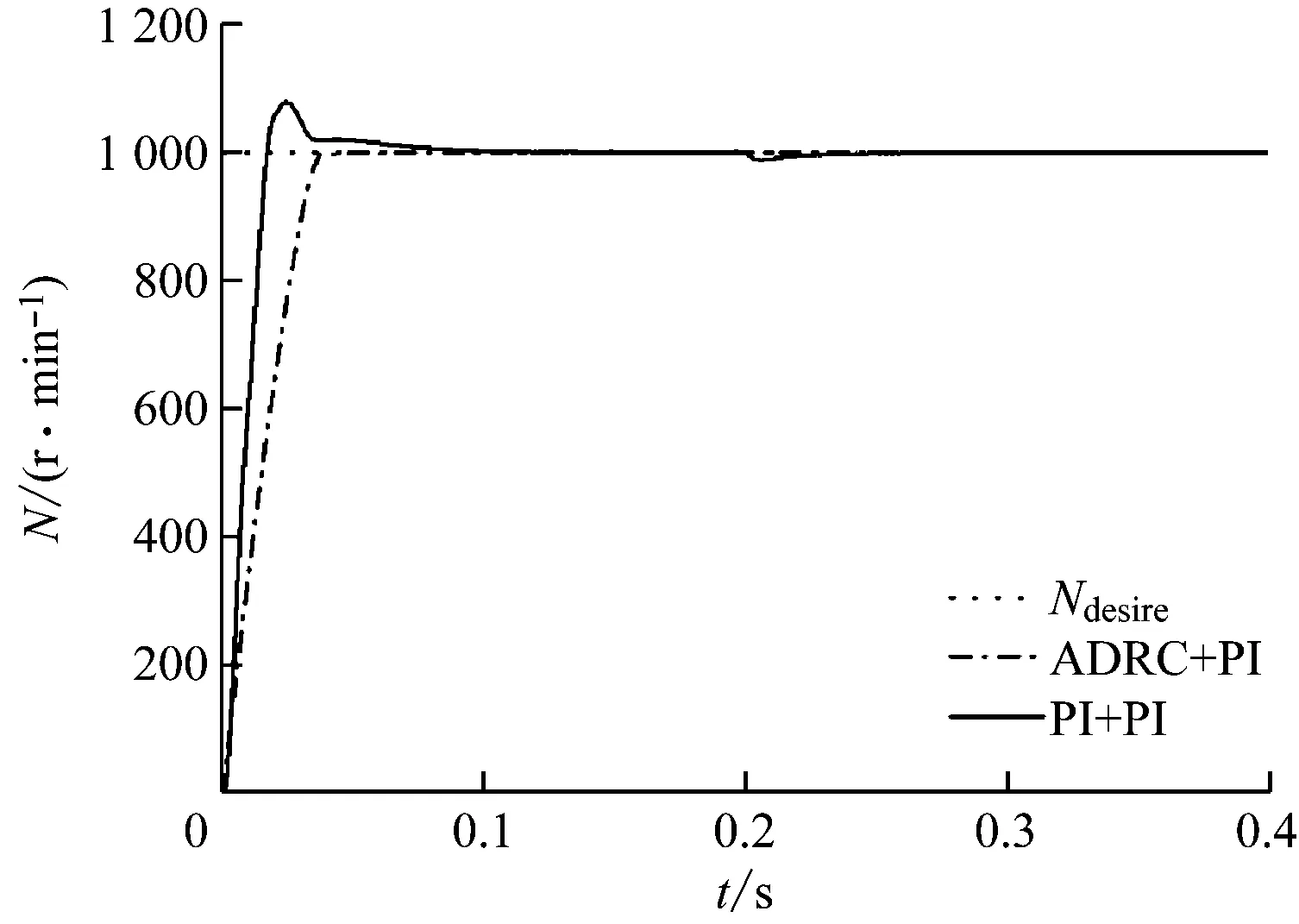
图7 平地直行工况下PMSM转速响应曲线Fig.7 Speed response curves of PMSM in straight driving condition on flat ground

平地直行工况下PMSM转矩Te响应曲线如图8所示。采用ADRC+PI方案时，PMSM转矩输出稳定且可精准跟踪期望值或外部扰动量，尤其当遇到外部转矩突变扰动时，也能快速恢复到给定参考值；但采用PI+PI方案时，PMSM转矩则存在一定的波动，无法实现对期望转矩的跟踪输出。

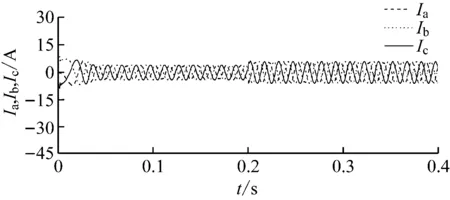
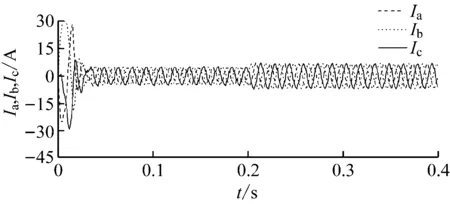
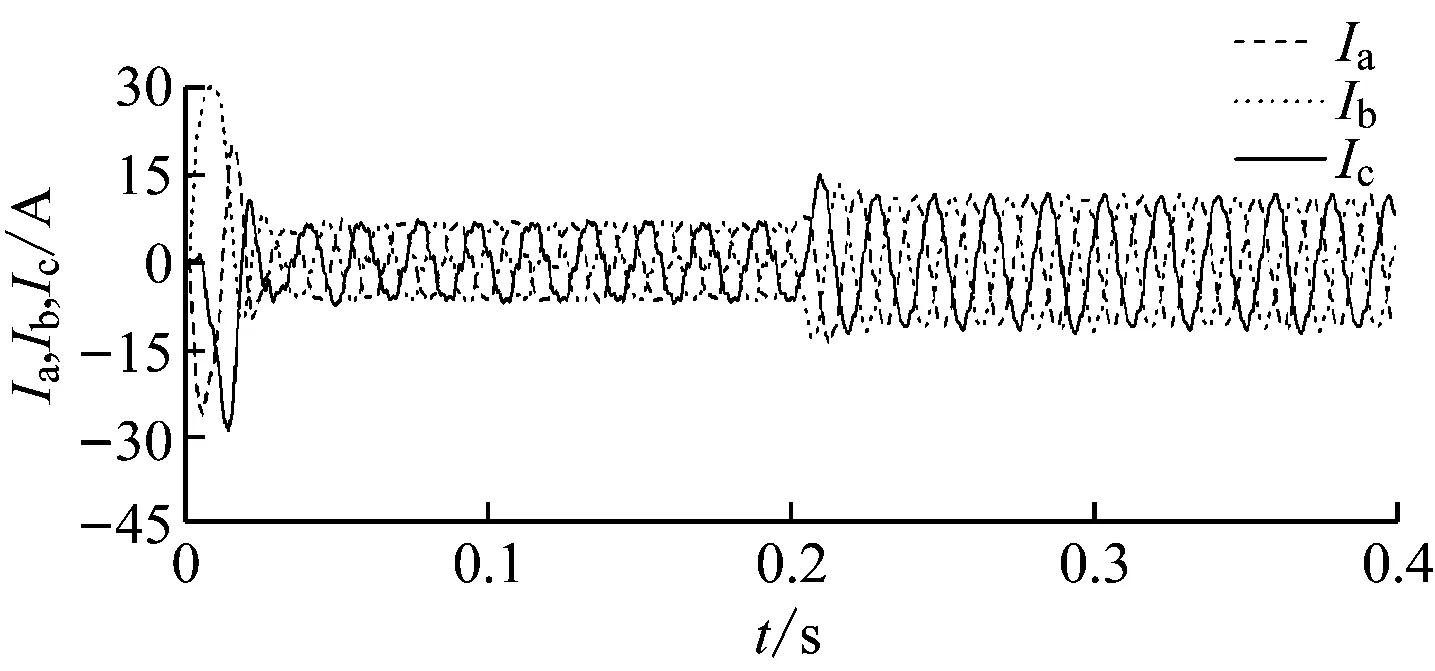
平地直行工况下PMSM相电流响应曲线如图9所示,Ia,Ib,Ic为三相电流。与PI+PI方案相比，采用ADRC+PI方案时，转速稳定，转矩输出平稳，因此PMSM的相电流幅值更稳定，在PMSM启动过程中，采用ADRC+PI方案时电流对PMSM的冲击更小，PMSM启动更平稳；而在突加负载的情况下，采用ADRC+PI方案的PMSM相电流调节时间更短、波动更小。

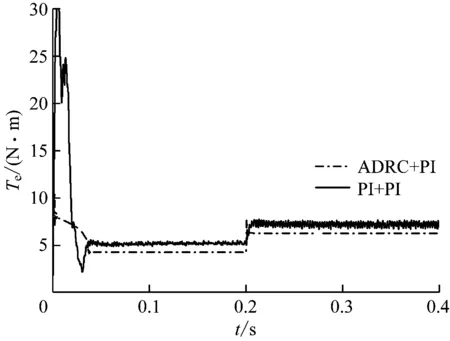
图8 平地直行工况下PMSM转矩响应曲线Fig.8 Torque response curves of PMSM in straight driving condition on flat ground

(a) ADRC+PI

(a) ADRC+PI

3.3 直行爬坡工况仿真

机器人爬坡时，电动机转矩比在平地行走时高，持续转矩为6.7 N·m。当电动机进入平稳期后，在t=0.2 s时引入4.7 N·m干扰量。

直行爬坡工况下PMSM转速响应曲线如图10所示。在PMSM启动阶段，速度环采用ADRC时产生一定超调，但超调量较小，仅为1.5%，但采用PI控制器时超调量较大，超过11%，且调节时间较长，为采用ADRC时的3倍。在0.2 s加入扰动后，采用PI控制器时摄动变化较明显，摄动幅度超过40 r/min，而采用ADRC时PMSM转速相对稳定，转速摄动幅度不超过10 r/min，抗干扰能力较强。

直行爬坡工况下PMSM转矩响应曲线如图11所示。可看出速度环采用ADRC时，PMSM的转矩输出稳定且跟踪精准，且在外部突变扰动状态下响应速度更快，跟踪能力更强。

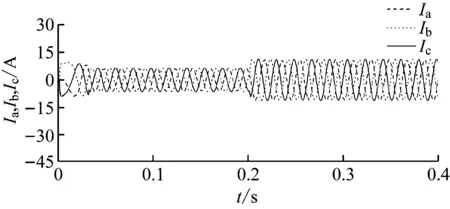
直行爬坡工况下PMSM相电流响应曲线如图12所示。速度环采用ADRC时，PMSM的相电流逼近正弦波，矢量控制精准，启动电流更小、更平稳，有利于提高PMSM控制性能并延长其工作寿命。

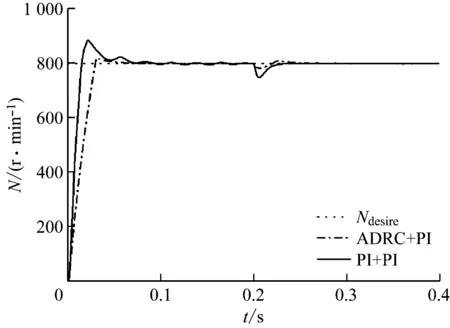
图10 直行爬坡工况下PMSM转速响应曲线Fig.10 Speed response curves of PMSM in straight climbing condition

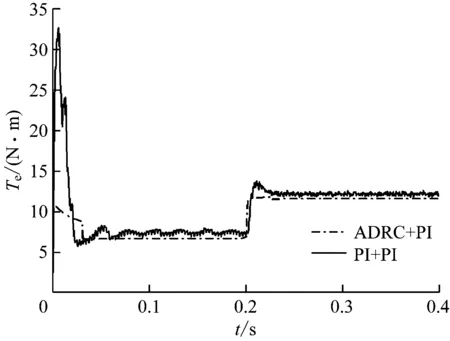
图11 直行爬坡工况下PMSM转矩响应曲线Fig.11 Torque response curves of PMSM in straight climbing condition

(a) ADRC+PI

(b) PI+PI

4 结论

(1) 设计了适用于非结构复杂路面环境的井下履带式探测机器人，并进行了爬坡越障性能分析，得出了平地直行和直行爬坡2种工况下机器人PMSM的转矩和转速。

(2) 对机器人PMSM进行数学建模，设计了速度环ADRC和电流环PI控制器，并采用FOC技术对PMSM进行驱动。

(3) 对ADRC+PI和常规PI+PI控制方案进行仿真和对比分析，得到2种工况下PMSM的转速、转矩、相电流响应曲线，结果表明：在2种工况下，采用ADRC+PI方案时机器人PMSM的转速和转矩响应控制更精准，具有更小的超调量和更短的调节时间，应对外部突变干扰的能力更强，能有效提升井下履带式探测机器人的爬坡越障性能和作业稳定性。