无砟轨道路桥过渡段动力分析
2022-03-04许思遥
许思遥
(湖南省交通科学研究院有限公司,湖南 长沙 410014)
列车通过路桥过渡段时,因路基与桥台刚度差异明显,列车和线路振动加剧,导致过渡段受力环境复杂,容易发生轨道变形、扣件丧失刚度等,不利于列车安全运行及过渡段正常服役。针对该问题,李双龙等以蒙华(浩勒报吉—吉安)重载铁路为背景,建立轮轨-路基耦合模型,研究过渡段刚度及轮轨接触力变化特性,认为倒梯形过渡段动力扩散效果优于一般路基;常文浩等以CRTSⅡ型板为研究对象,建立严寒地区路桥过渡段无砟轨道有限元模型,研究过渡段冻胀对过渡段的影响,认为过渡段长度较小时,冻胀变形会导致路桥过渡段层间离缝严重;李泰灃等建立轻质填料路桥过渡段模型,分析列车荷载作用下轻质填料路桥过渡段的动力响应,结果表明轻质填料路桥过渡段的动力性能满足高速铁路运营标准;周文涛等建立CRTSⅡ型板式无砟轨道路桥过渡段数值模型,计算列车和路桥过渡段的动力响应,认为随过渡段不均匀沉降增大,过渡段列车和轨道的动力响应明显增大,应严格控制过渡段不均匀沉降。为模拟列车-轨道-路桥过渡段真实工作状态,并减少现场测量,该文以CRTSⅡ板式无砟轨道为研究对象,建立列车-轨道-路桥过渡段有限元模型,计算不同工况下列车与轨道的动力响应并分析其特性,为路桥过渡段优化设计提供参考。
1 列车-轨道-路桥过渡段模型构建
1.1 列车模型
列车以CRH3为研究对象,考虑车体、两系悬架、转向架及轮对。为提高计算效率并保证结果准确,适当简化列车结构,车体、转向架及轮对采用刚体模型(见图1)。
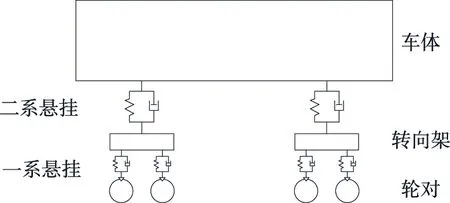
图1 列车模型
基于牛顿第二定律和动量矩理论建立列车动力方程:
(1)
式中:M、C、K分别为质量、阻尼和刚度矩阵;X为列车广义位移向量;F为列车广义荷载向量;t表示列车。
根据式(1),利用ABAQUS多体动力模块建立列车数值模型,列车的动力参数见表1,列车有限元模型见图2。

表1 列车的动力参数

续表1

图2 列车有限元模型
1.2 轨道模型
因轮轨相互作用较复杂,轨道模型采用连续分布模型,相关部件均采用实体单元。CRTSⅡ型板式无砟轨道由钢轨、支撑层、CA砂浆及轨道板构成,轨道有限元模型见图3。钢轨模型(见图4)采用60 kg/m钢轨,相关参数见表2。

图3 轨道有限元模型

图4 钢轨有限元模型

表2 钢轨的截面尺寸及特性
扣件间距取0.6 m,亦为单节钢轨长度。针对硬轨道振动特性,钢轨单元尺寸取0.6 m。利用Merge将350个单节钢轨合并,钢轨总长度为210 m。为快速准确建模,利用MATLAB编写子程序,批量建立Wire,模拟扣件形态。
1.3 路基模型
路基结构分3层,逐层填筑,基床上为压实性级配碎石,底层为填料组A、B,路基采用压实土。采用ABAQUS软件建立路基有限元模型,路基采用C3D8R单元模拟,基本尺寸为500 m×13 m×5 m(长×宽×高),边坡坡度1∶1.5。路基结构剖面见图5,有限元模型见图6。

图5 路基剖面(单位:m)

图6 路基有限元模型
1.4 桥梁模型
以二跨箱形简支桥梁为研究对象,单跨长30 m,其纵向刚度为400 kN/cm。桥梁相关参数见表3,桥梁剖面见图7,有限元模型见图8。

表3 桥梁的材料属性
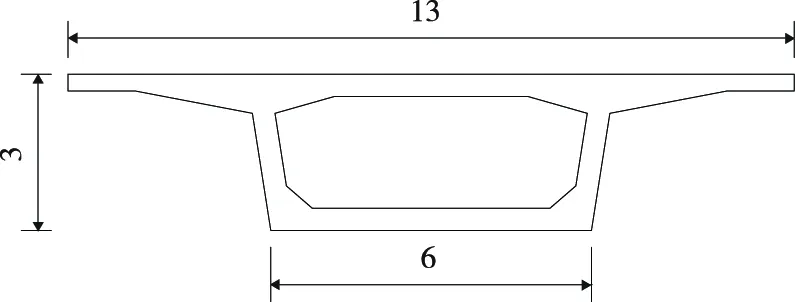
图7 桥梁剖面(单位:m)

图8 桥梁有限元模型
1.5 列车-轨道-路桥过渡段模型
过渡段形式为倒梯形,其模型见图9。过渡段长度按式(2)计算,过渡段有限元模型见图10。

图9 路基-过渡段-桥梁连接剖面
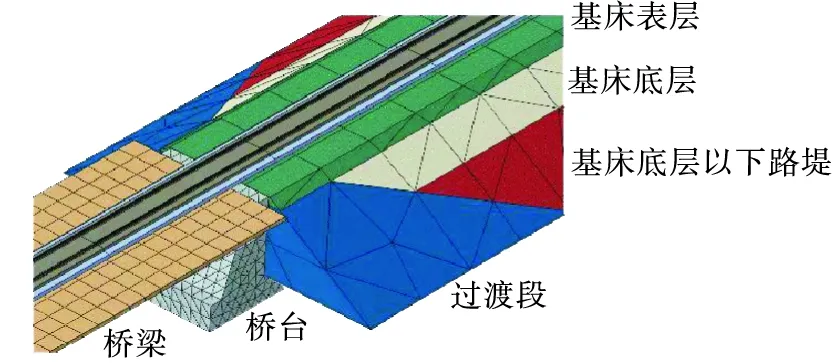
图10 轨道—路桥过渡段模型
L=a+(H-h)n
(2)
基于相关链接属性,将上述模型在Assembly模块中装配。考虑列车与轨道轮轨的接触关系,建立轮轨接触属性,模拟轮轨动态接触。根据赫兹理论,轮轨接触关系与轮轨接触力、相对位移、接触材料性质及接触面形状有关,将钢轨和车轮视为圆柱体,由赫兹公式得:
y=Gp2/3
(3)
式中:y为轮轨法向相对位移;G为钢轨挠度系数,其值为4.57R-0.149×10-8,车轮为磨耗性踏面时取3.86R-0.149×10-8,R为车轮半径;p为轮轨法向接触力。
轮轨接触模型见图11。

图11 轮轨接触模型
2 列车-轨道-路桥过渡段动力分析
2.1 列车运行安全性指标
高速铁路规范采用列车运行安全性作为评价列车动力响应的主要依据,具体评价指标有脱轨系数和轮重减载率。
(1)脱轨系数。式(4)为脱轨系数表达式。根据文献[5],脱轨系数安全指标如下:H/F≤1.2为危险限度,H/F≤1.0为容许限度。
脱轨系数=H/F
(4)
式中:H为车轮横向力;F为车轮纵向力。
(2)轮重减载率。式(5)为轮重减载率表达式。根据文献[5],轮重减载率安全指标如下:ΔP/P≤0.65为危险限度,ΔP/P≤0.60为容许限度。
轮重减载率=ΔP/P
(5)
式中:ΔP为轮重减载量;P为平均净轮重。
2.2 列车运行平稳性评价指标
旅客乘车舒适度由列车运行平稳性来评价。采用列车垂向振动加速度和横向振动加速度作为列车运行平稳性评价指标,评价标准见表4。

表4 列车振动加速度评价标准
2.3 轨道结构动力响应评价
由于桥梁和路基刚度不同,列车高速通过桥梁和路基连接部分会加剧轮轨冲击作用,对轨道几何形位、轨道结构稳定及路基结构产生不利影响。采用轮轨垂向力和轮轨横向力评价高速铁路路桥过渡段轨道结构的动力响应。
(1)轮轨垂向力。轮轨垂向力由轮轨垂向振动产生。为限制轮轨振动幅度,《高速试验列车动力强度及动力学性能规范》规定,列车通过道岔、桥梁、曲线等部位时,最大垂向作用力不大于170 kN。
(2)轮轨横向力Q。轨道结构存在轨道不平顺、路基刚度不均匀等,会导致轮轨横向力过大,引起轨道横向变形、扣件损伤及列车脱轨。轮轨横向力评价标准为Q≤43.8 kN。
3 动力特性分析
建立列车-轨道-路桥过渡段有限元模型,采用ABAQUS/Explicit求解器计算,分析不同过渡段长度和不同过渡段填料弹性模量下轨道和列车的动力响应。
3.1 过渡段长度对轨道动力响应的影响
依次计算不同过渡段长度下轨道垂向力和三向振动加速度等动力学指标,分析过渡段长度对轨道动力响应的影响,结果见图12~15。
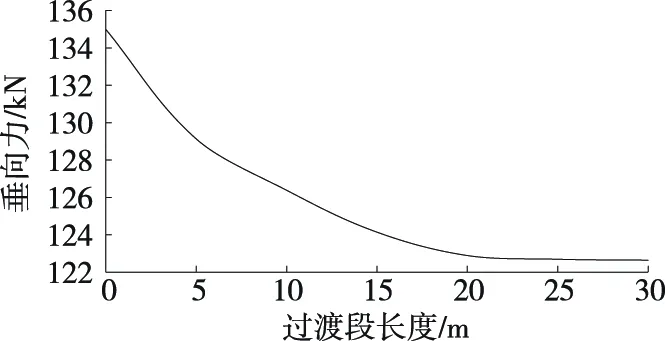
图12 过渡段长度对轮轨垂向力的影响
由图12可知:无过渡段时,轮轨垂向力为135.3 kN;轮轨垂向力随着过渡段长度的增大逐渐降低,过渡段长度为15、20、25、30 m时,轮轨垂向力分别为124.4、123.1、122.9、122.9 kN。表明过渡段长度达到20 m后,继续增加过渡段长度对降低轮轨垂向力无明显作用。
由图13可知:无过渡段时,轮轨垂向加速度为242g;轮轨垂向加速度随着过渡段长度的增大逐渐降低,过渡段长度为15、20、25、30 m时,轮轨垂向加速度分别为222.5g、220.3g、218.5g、218.3g。表明过渡段长度达到20 m后,继续增加过渡段长度对降低轮轨垂向加速度无明显作用。
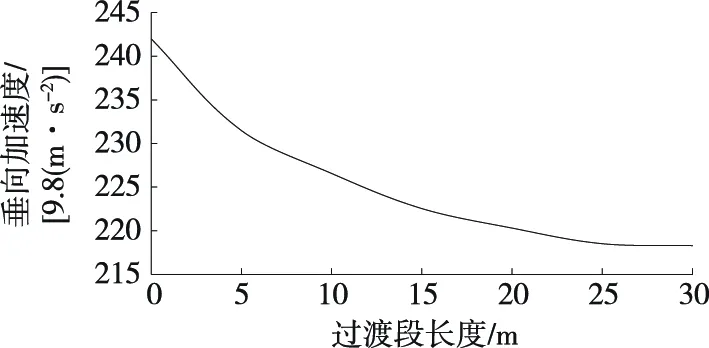
图13 过渡段长度对轮轨垂向加速度的影响
由图14可知:无过渡段时,轮轨横向加速度为449.8g;横向加速度随着过渡段长度的增大略有降低,但衰减幅度并不明显,与过渡段长度为20 m时相比,过渡段长度为30 m时横向加速度仅降低0.20%。

图14 过渡段长度对轮轨横向加速度的影响
由图15可知:无过渡段时,轮轨纵向加速度为394.8g;纵向加速度随着过渡段长度的增大趋于平缓;过渡段长度为20 m时,纵向加速度比无过渡段时降低0.33%。

图15 过渡段长度对轮轨纵向加速度的影响
3.2 过渡段长度对列车动力响应的影响
依次计算不同过渡段长度下列车的轮重减载率、脱轨系数、车体垂向加速度,分析过渡段长度对列车动力响应的影响,结果见图16~18。

图16 过渡段长度对列车轮重减载率的影响
由图16可知:无过渡段时,列车轮重减载率为0.638,大于容许限度;过渡段长度为5 m时,轮重减载率为0.546,小于容许限度;过渡段长度小于15 m时,随着过渡段长度的增大,轮重减载率明显降低;过渡段长度大于15 m时,随着过渡段长度的继续增大,轮重减载率无明显变化。
由图17可知:无过渡段时,脱轨系数为0.460;过渡段长度增加为20 m时,脱轨系数为0.235,比无过渡段时减小48.9%;过渡段长度大于20 m,继续增加过渡段长度,脱轨系数变化不明显。
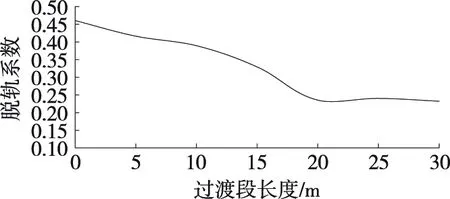
图17 过渡段长度对列车脱轨系数的影响
由图18可知:无过渡段时,列车垂向加速度为0.138g;列车垂向加速度随着过渡段长度的增加逐渐减小,过渡段长度达到20 m时列车垂向加速度为0.060g,比无过渡段时减小56.5%;继续增加过渡段长度,列车垂向加速度变化不明显。
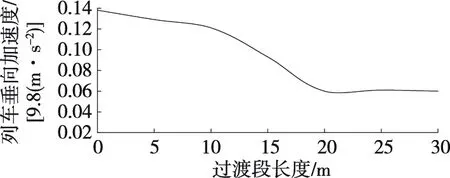
图18 过渡段长度对列车垂向加速度的影响
3.3 过渡段填料对轨道动力响应的影响
依次计算不同过渡段填料(填料不同弹性模量)下轨道三向振动加速度,分析过渡段填料对轨道动力响应的影响,结果见图19~21。

图19 过渡段填料对钢轨垂向加速度的影响
由图19可知:填料弹性模量为80~90 MPa时,钢轨垂向加速度无明显变化;填料弹性模量为90~120 MPa时,随着填料弹性模量的增加,钢轨垂向加速度逐渐减少,与填料弹性模量为90 MPa时相比,填料弹性模量为120 MPa时钢轨垂向加速度减小22.43%,填料弹性模量在该范围内对钢轨垂向加速度有明显影响;填料弹性模量为120~140 MPa时,钢轨垂向加速度趋于平缓;填料弹性模量大于150 MPa时,钢轨垂向加速度略有增加。
由图20可知:填料弹性模量为80~120 MPa时,轨道板垂向加速度随填料弹性模量的增加逐渐减小,与填料弹性模量为80 MPa时相比,填料弹性模量为120 MPa时轨道垂向加速度减小24.22%;填料弹性模量为120~150 MPa时,随填料弹性模量增加,轨道板垂向加速度无明显变化;填料弹性模量大于150 MPa时,轨道板垂向加速度略有上升。

图20 过渡段填料对轨道板垂向加速度的影响
由图21可知:填料弹性模量为80~90 MPa时,支撑层垂向加速度变化不明显;填料弹性模量为90~110 MPa时,随填料弹性模量增加,支撑层垂向加速度逐渐减小,与填料弹性模量为80 MPa时相比,填料弹性模量为110 MPa时支撑层垂向加速度减小15.6%;填料弹性模量大于110 MPa,随着填料弹性模量的增大,支撑层垂向加速度无明显变化。

图21 过渡段填料对支撑层垂向加速度的影响
3.4 过渡段填料对列车动力响应的影响
依次计算不同过渡段填料下列车的轮重减载率、脱轨系数、车体垂向加速度,分析过渡段填料对列车动力响应的影响,结果见图22~24。

图22 过渡段填料对列车轮重减载率的影响
由图22可知:填料弹性模量为80~90 MPa时,列车轮重减载率无明显变化;填料弹性模量为90~110 MPa时,随填料弹性模量增大,列车轮重减载率逐渐降低,与填料弹性模量为90 MPa时相比,填料弹性模量为120 MPa时轮重减载率减小31.34%;填料弹性模量为110~150 MPa时,轮重减载率无明显变化,趋于平稳;填料弹性模量大于150 MPa时,轮重减载率随着填料弹性模量的增大而逐渐增大。
由图23可知:列车脱轨系数随填料弹性模量增加而逐渐减小;填料弹性模量为100~120、130~140 MPa时,脱轨系数趋于平缓;填料弹性模量为80、90 MPa时,脱轨系数较大,分别为0.469、0.464,均未超过容许限度。

图23 过渡段填料对列车脱轨系数的影响
由图24可知:填料弹性模量为80~120 MPa时,随着填料弹性模量的增大,列车垂向加速度减小,与填料弹性模量为80 MPa时相比,填料弹性模量为120 MPa时列车垂向加速度降低58.62%;填料弹性模量为120~140 MPa时,列车垂向加速度趋于平缓;填料弹性模量大于150 MPa时,列车垂向加速度略有增加。

图24 过渡段填料对列车垂向加速度的影响
4 结论
(1)路桥过渡段长度为0~20 m时,轨道和列车的动力响应随着路桥过渡段长度的增大逐渐降低;过渡段长度大于20 m时,列车和轨道的动力响应随着过渡段长度的继续增大无明显变化。
(2)随着过渡段填料弹性模量的增大,列车脱轨系数逐渐减小;过渡段填料弹性模量为80~110 MPa时,其他动力响应随填料弹性模量的增大逐渐降低;过渡段填料模量大于140 MPa时,列车动力响应增大。
