基于高压氮气充气试验的气体状态方程对比研究
2022-03-04王堃*
王 堃 *
(海军装备部)
0 引言
用于存贮高压气体的气瓶广泛应用于石油、化工、军事等工业,如压缩天然气(CNG)瓶、高压氢气瓶、医用高压氧气瓶、用于液体火箭发动机的高压气瓶(氮气、氦气等)等[1-3]。
气体状态方程是用于描述气体基本热物性参数之间的函数关系,也是高压气瓶设计的基础。气体状态方程包括理想气体状态方程和实际气体状态方程。高压气瓶内的气体压力较高,往往高于15 MPa;在较高压力下,气体的非理想性将会逐渐显著,采用理想气体状态方程计算则会产生较大误差[4-5]。
本文对3 种常用的气体状态方程(理想气体方程、范德瓦尔方程以及Redlich-Kwong 方程)进行了描述和分析。并以氮气为介质开展了充气试验,最后将充气质量和充气压力的试验结果与3 种方程进行了对比分析。
1 气体状态方程
1.1 理想气体状态方程
理想气体是对实际气体简化后建立的一种理想模型。理想气体具有以下两个特点:(1)分子本身不占有体积;(2)分子间无相互作用力。实际应用中,温度不太低、压强不太高条件下的气体可近似看作理想气体,而且温度越高、压强越低,越接近于理想气体。如上所述,由于理想气体的特性,气体密度与气体温度、压力呈简单线性关系。理想气体状态方程如式(1)所示:

式中:p——气体压力,MPa;
v——气体比体积,v=V/m,m3/kg;
V——气体体积,m3;
m——气体质量,kg;
Rg——气体常数,J/(kg·K);
T——气体温度,K。
1.2 范德瓦尔气体状态方程
针对实际气体和理想气体假设之间的差别,范德瓦尔方程考虑了实际气体分子本身的体积以及分子之间的引力的影响,对理想气体状态方程式进行了修正,提出了最早的实际气体状态方程——范德瓦尔方程[6],如式(2)所示:
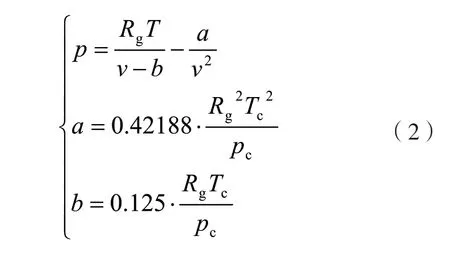
式中:a——修正数,考虑分子之间有吸引力,与气体本身性质有关,(m6·Pa)/ kg2;
b——修正数,考虑分子本身有体积,与气体本身性质有关,m3/kg;
Tc——气体临界温度,K;
pc——气体临界压力,Pa。
1.3 Redlich-Kwong气体状态方程
德里(Redlich)和匡(Kwong)在范德瓦尔方程的基础上提出了含有两个常数的R-K 方程,保留了范德瓦尔方程中体积的三次方程的简单形式。R-K方程通过对内压力项(a/v2)进行修正,进一步提高了计算精度[7],如式(3)所示:

式中:aa——修正数,考虑分子之间有吸引力,与气体本身性质有关,(m6·Pa·K0.5)/ kg2;
bb——修正数,考虑分子本身有体积,与气体本身性质有关,m3/kg。
1.4 状态方程比较
针对氮气工质,根据文献[6-7]可计算得到范德瓦尔方程和R-K 方程的修正数,可见表1。

表1 范德瓦尔方程和R-K方程的氮气修正数
通过3 种状态方程分别计算了20 ℃时,氮气在0.1~50 MPa 压力下的密度,计算结果如图1 所示。在温度不变的条件下,理想气体状态方程计算的密度与压力成正比关系,整个压力范围气体密度与压力呈线性关系;当压力较低时(15 MPa 以下),范德瓦尔方程与R-K 方程计算得到的密度,与理想气体状态方程的计算结果基本一致;随着压力逐渐升高,氮气分子间间距逐渐减小,分子间作用力逐渐增大,压力增长对密度增长的作用越来越有限,计算得到的密度增长逐渐放缓。当压力为50 MPa 时,范德瓦尔方程和R-K 方程计算的密度分别为400.9 kg/m3和438.3 kg/m3,较理想气体状态方程计算结果相比分别减少了30.1%、23.7%。高压情况下三种方程的计算结果差异较大。
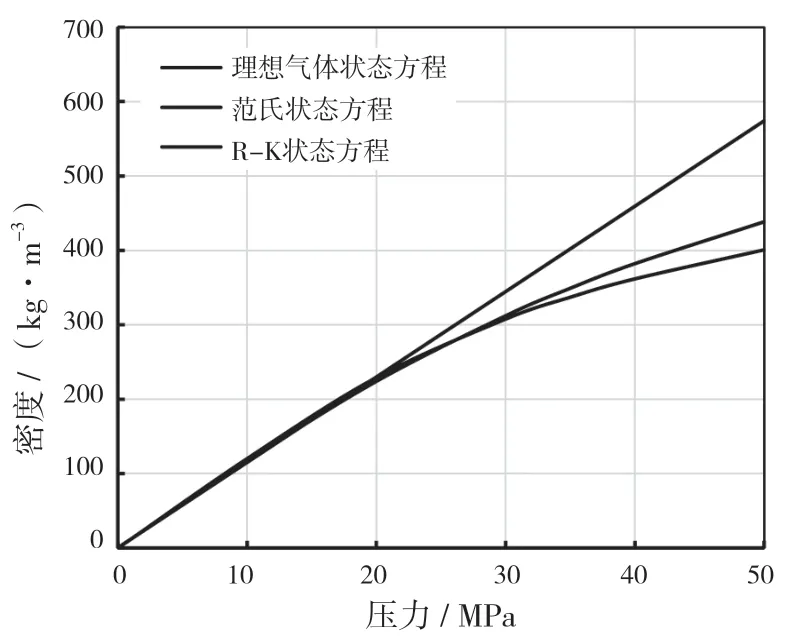
图1 密度计算结果对比
2 充气试验
为了分析3 个状态方程的计算精度,开展了以氮气为介质的充气试验,试验系统如图2 所示。试验系统主要由高压气源、恒温箱、气瓶、电子秤、压力、温度传感器及数据采集设备等构成。气瓶标称容积为4.00 L,充气压力为20~40 MPa,恒温箱温度为20~65 ℃。压力传感器用于测量气瓶内压力,量程为0~50 MPa,精度为0.5%;温度传感器用来测量气瓶表面温度,考虑到气瓶表面温度可能分布不均,因此设置了3 个T 型热电偶,计算时取平均温度,热电偶的测温范围为0~100 ℃,精度为1%。
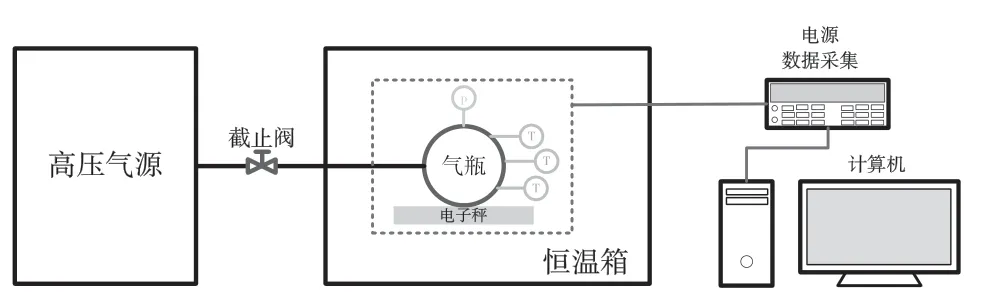
图2 充气试验系统示意图
通过上述试验系统开展了两项试验:(1)常温充气称重试验;(2)充气后气瓶压力随温度变化试验。常温充气称重试验是通过试验确定温度恒定时,气体密度与气体压力的关系;气体压力随温度变化试验则是通过试验确定密度恒定时,气体压力与气体温度之间的关系。上述温度、压力、密度的试验结果可以用于对比三种状态方程的计算结果。
2.1 称重试验
进行了4 个工况的充气试验,试验压力分别为20、30、35、40 MPa,环境温度为20.0 ℃。每一个工况试验时,恒温箱不工作,充气后断开截止阀,当气瓶温度与环境温度平衡时,通过压力传感器和电子秤测量并记录气体压力和质量。
为了更加准确地评价各状态方程的精度,充气容积考虑了气瓶接嘴至截止阀前管路容积与压力传感器容积,并考虑了充压后气瓶尺寸增大带来的气瓶容积变化。
试验结果与三种状态方程计算结果如图3 所示。以试验结果为基准,统计各状态方程的偏差可见表2。
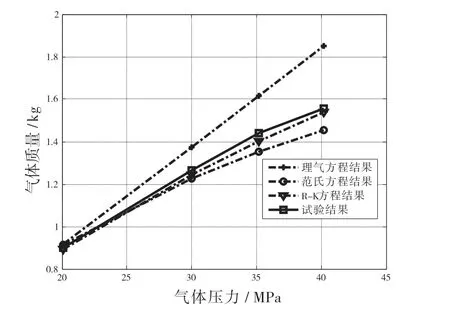
图3 称重试验结果
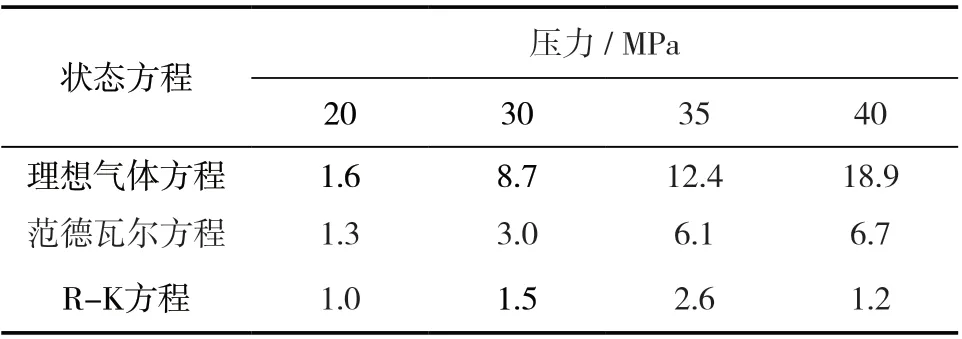
表2 状态方程计算偏差 %
从上述试验结果可以看出,充气质量随着充气压力提高而增大,但随着压力提高,充气质量增长的幅度也越来越小,即温度一定时,气体密度随着压力提高而增大,但变化率越来越小。3 种气体状态方程计算得到的充气质量与充气压力变化趋势与试验结果一致,但由于高压下气体的非理想性显著提高,因此理想气体状态方程计算结果与试验结果的偏差随着压力提高而逐渐增大。当充气压力为20 MPa 时,理想气体状态方程的偏差可以控制在1.6%以内;当充气压力大于30 MPa 时,偏差大于8.7%;充气压力为40 MPa 时,偏差则达到了18.9%。与理想气体状态方程相比,两种实际气体状态方程的计算结果与试验结果吻合较好,当充气压力在40 MPa 内,范德瓦尔方程的偏差在6.7%以内;R-K 方程的偏差最小,最大偏差为2.6%。
2.2 温度试验
首先恒温箱不工作,环境温度为20.0 ℃,向气瓶内缓慢充入38 MPa 的氮气,并在1 h 后补气,补气后稳定2 h,压力传感器测量气瓶内压力为37.97 MPa;关闭截止阀,控制恒温箱缓慢升温至65.0 ℃,气瓶温度稳定后,压力传感器测量气瓶内压力为46.5 MPa,随后2 h内该压力值未发生变化。
对于初始状态相同的氮气(20 ℃、37.97 MPa),通过三种状态方程计算温度为65.0 ℃时的气瓶压力。试验结果与计算结果的对比情况如表3 所示。理想气体方程、范德瓦尔方程、R-K 方程的计算结果分别为43.8、47.1、46.4 MPa。以试验结果为基准,三个状态方程的计算误差分别为:5.8%、1.3%、0.2%。与称重试验结果类似,当压力高于40 MPa 时,R-K方程计算结果与试验结果最接近,范德瓦尔方程次之,理想气体方程计算偏差较大。

表3 温度试验结果
3 状态方程讨论
气瓶压力较低(15 MPa 以下)时,气体分子间距较大,分子之间的作用力较小,接近理想气体状态。采用理想气体状态方程计算得到气体的热物性参数,计算值与实测值的误差不大。因此,在压力较低的情况下,利用理想气体状态方程来计算气瓶设计参数,并通过经验性参数(设计容积裕度等)修正,可以得到比较满意的结果。
当气瓶内压力较高时,气瓶在充气过程中容积略微增大会在一定程度上弥补理想气体状态方程的计算误差,但是随着压力升高,气体分子之间的间距逐渐缩小,分子之间的作用力越来越大,这种弥补作用越来越弱化,气体分子体积、气体分子之间的作用力已不能被忽略,理想气体状态方程难以满足设计需求。当气瓶设计压力较高(15 MPa 以上)时,需要采用实际气体状态方程。对称重试验、温度试验的结果进行分析后可知,当压力较高时,采用R-K 方程计算得到的结果与试验结果最接近,计算误差最小,因此进行高压气瓶设计时建议采用R-K 方程。
4 结论
本文对3 种气体状态方程(理想气体状态方程、范德瓦尔气体状态方程和R-K 气体状态方程)进行了说明和对比。高压氮气充气试验结果表明:R-K方程的计算精度最好,能更准确地表征实际气体p-v-T关系。在对高压气瓶(特别是设计压力大于15 MPa 的高压气瓶)进行设计计算时可以采用R-K方程。
