考虑作息时间的流水车间调度模型与算法*

2022-03-04任丹妮熊禾根阳光灿

组合机床与自动化加工技术 2022年2期

任丹妮，熊禾根，阳光灿

(武汉科技大学a.冶金装备及其控制教育部重点实验室;b.机械传动与制造工程湖北省重点实验室,武汉 430000)

0 引言

流水车间调度问题(flow-shop scheduling problems,FSP)是当前很多以流水线方式生产的制造车间调度的抽象模型，作为一个离散的非数值化优化问题，也被证明是一个典型的NP-hard问题，具有很高的理论研究价值和实践价值[1]。

在实际生产过程中，流水车间调度模型的建立中存在各种不确定因素和资源约束条件，如机器具有不可用时间限制的约束。LEE[2]研究了当工件是部分可恢复时，机器具有不可用时间间隔的双机FSP；SAFARI等[3]将实际生产过程中机器需要进行预防性维护以及可能发生故障的约束条件加入FSP，提出了此类问题的流水车间调度模型；AGGOUNE等[4]假设机器存在周期性的不可用时间段，设计了结合启发式规则的禁忌搜索算法，有效地提高了加工效率。

为了实现FSP的最优调度求解，国内外很多学者也做了大量的研究。遗传算法由于较好的搜索能力被广泛应用，NEPPALLI等[5]提出解决双机双目标FSP的遗传算法；KARIMI等[6]提出解决混合FSP的多阶段遗传算法；DUGARDIN等[7]提出的求解可重入FSP的多目标改进遗传算法。当传统单一算法难以得到最优解时，通常可以选择混合算法使保持多样性与搜索最优解的能力相平衡，王芳等[8]提出了结合瓶颈启发式的引力搜索算法用于解决柔性FSP；TSENG等[9]利用遗传算法进行全局搜索，再结合两种局部搜索解决了FSP最小化流程时间目标；轩华等[10]提出结合迭代贪婪算法的混合遗传融合优化策略对解决实际柔性流水车间的多处理器调度问题能够获得较好的近似解；吴永明等[11]提出了解决无等待FSP的改进蛙跳算法，其中结合高斯变异和扰动因子，提高了局部搜索及全局搜索能力。

即使已有研究考虑到机器的不可用状态，但是很少有研究考虑到车间存在作息时间导致的机器不可用问题，导致调度方案不能很好地指导实际应用。因此，本文针对考虑作息时间的流水车间调度问题(flow-shop scheduling problem with consideration of timetable of work,FSP-CTW)进行研究，提出相关调度模型与改进算法，在一定程度上保证了调度方案与实际生产调度相吻合，提高生了产效率，具有明确的现实意义，符合企业的实际生产需求。

1 考虑作息时间的流水车间调度模型

1.1 问题描述

流水车间调度问题可以描述为：n个工件以相同的顺序经过m台机器，每台机器上工件加工顺序相同。给定工件在各机器上的加工时间，安排工件的加工优先级，在满足工件加工的工艺顺序约束与机器加工工件的先后顺序约束条件下，实现调度目标。

考虑作息时间的流水车间调度问题不仅要满足FSP的约束条件，还要满足工件加工的开始时刻、完成时刻在工作时段内，即机器的可用时段内，达到调度目标。与FSP相比，FSP-CTW虽然在解的空间上没有变化，但新添了约束条件，也增加了问题求解的难度。对FSP-CTW做出如下假设：

(1)给定不同工作时段数的工作时间与休息时间；

(2)工作制、工作时间段数、工作日的开始工作时刻设定后，在调度过程中保持不变；

(3)同一时刻，一台机器只能加工一个工件，且一个工件只能被一台机器加工；

(4)加工无抢占性，即不允许任意工件的加工插入另一工件的加工过程中；

(5)不同工件的加工优先级相同；

(6)给定工序加工是否可恢复；

(7)不考虑机器故障、机器维护、机器维修等动态因素；

(8)不考虑机器调整时间、工件运输时间，将其计入对应的加工时间内；

(9)工件在机器上的加工顺序确定后，不再改变。

1.2 数学模型

为建立该问题的数学模型，首先根据问题描述定义相关符号与决策变量如表1所示。

表1 相关符号及含义

续表

其中，aij=1表示工序Oij的加工可恢复，即工序Oij的加工可跨越工作时段，在工作时段的结束时刻，工序Oij剩余的加工可在下一工作时段继续进行；aij=0表示工序Oij的加工不可恢复，即工序Oij的加工不可跨越工作时段，工序Oij的加工开始时刻、完成时刻均要在同一工作时段内；zijkt=1表示工序Oij的加工过程包含工作时段Mkt，即工序Oij的加工开始时刻或完成时刻在工作时段Mkt内；zijkt=0表示工序Oij的加工过程不包含工作时段Mkt，即工序Oij的加工开始时刻或完成时刻不在工作时段Mkt内。

定义决策变量以确定工件在机器上的加工顺序：

(1)

目标函数为最小化最大完工时间：

MinimizeCmax=Cim,Xin=1

(2)

约束条件如下：

(3)

(4)

Sij≥ri,∀i∈J,j∈U

(5)

Sij≥Ci(j-1),∀i∈J,j∈Ji∧j>1

(6)

Sgh≥Cij,∀i,g∈J,j=h∈U,p,q∈J,i≠g,pXgp>qXiq

(7)

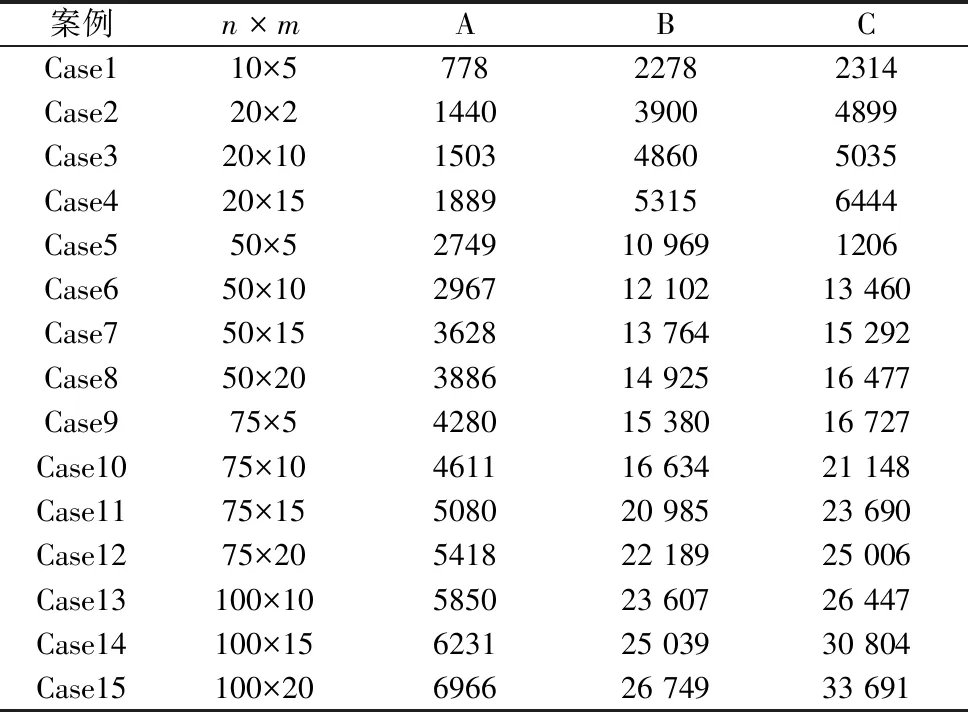
Wkt≤Sij

(8)

Wkt

(9)

(10)

(11)

(12)

式中，J表示工件集合；U表示机器集合和工序集合；Q表示工作时段集合。式(3)表示一个工件能且只能占一个加工位置；式(4)表示一个加工位置能且只能被一个工件占用；式(5)表示工件的加工开始时刻不得早于工件的释放时刻；式(6)约束了同一工件的加工开始时刻与完成时刻；式(7)约束了同一机器上不同工件的加工开始时刻与完成时刻；式(8)表示存在某个工作时段，满足对任意工件的加工开始时刻大于等于其工作时段的开始时刻，小于其工作时段的结束时刻；式(9)表示存在某个工作时段，满足对任意工件的加工完成时刻大于其工作时段的开始时刻，小于等于其工作时段的结束时刻；式(10)表示若工件加工可恢复，则工件的加工过程可以包含多个工作时段，即工件的加工开始时刻、完成时刻可以在不同的工作时段内；式(11)表示若工件加工不可恢复，则工件的加工过程能且只能在一个工作时段内完成，即工件的加工开始时刻、完成时刻必须在同一工作时段内；式(12)表示工序的加工完成时刻与加工开始时刻、加工时间、工序加工过程所包含的工作时段的关系。

1.3 作息时间设计方法

为方便对FSP-CTW进行研究，作息时间的设计通过设置每台机器上的工作制、工作时段数、工作时间与休息时间来实现。比如，一个机器数量为3的FSP-CTW的作息时间设计如图1所示。

图1 作息时间设计示例

以机器1作详细说明。依次从左往右看，5表示机器1为5天工作制；0 1 2 3 4表示周一至周五工作；8表示每个工作日的调度起始时刻为8:00；2表示每个工作日有两个工作时间段；4表示第一个工作时段的工作时间为4 h；1表示第一个工作时段的休息时间为1 h；5表示第二个工作时段的工作时间为5 h；-1表示一个工作日的结束并自动确定休息时长，其余行以此类推。作息时间设计将人与机器分离，不从排班角度考虑设置机器的可用时段，而从机器本身的可用时段进行考虑，具有简单高效、包含的信息较为全面的优点。

2 求解FSP-CTW的改进遗传算法

遗传算法是一种高效的全局搜索方法，它能在搜索过程中不受搜索空间的局限，从种群开始利用适应度函数和概率转移策略指导其自动获取相关搜索空间的内容，并且能自适应地控制搜索过程以便求得最优解，在车间调度问题中得到很好的应用[12]。

但是传统遗传算法在解决确定型流水车间调度问题时，其计算结果往往趋于不稳定，容易陷入过早收敛和局部化最优。基于对作息时间的考虑，本节对传统遗传算法做了相应的改进。对流水车间调度模型采用了基于工件的编码，创建染色体和初始化种群，进行选择、交叉、变异等一系列操作后，利用了禁忌搜索改进遗传算法的局部搜索能力，提高解的质量。

2.1 编码与解码

有效的编码在不产生非法解的情况下能表达出个体与可行解的关系。对流水车间调度模型染色体主要采用基于工件的十进制编码方式。以6个工件为例，316245表示为每一台机器上均以工件3开始加工并依次加工余下工件，也代表了问题的一个解。

不同的解码方式产生的最大完工时间及机器的利用效率也会不同。在FSP-CTW中，由于休息时间段的存在，因此，在解码过程中需要考虑工件加工可恢复与不可恢复情形，如图2所示。从图中可知加工可恢复与加工不可恢复对工件的加工完成时刻存在明显影响。

图2 工件加工可恢复与不可恢复的解码示例

2.2 选择

为尽可能让适应度高的个体被保留，本文选择后代个体的方式是以轮盘赌策略为基础，辅以精英策略相结合。轮盘赌策略可有效防止问题的解步入局部最优化陷阱，精英策略则确保种群向更高质量的方向进化，两者有效结合，加速了种群的迭代和求解速度。

2.3 交叉与变异

在遗传算法中，交叉操作是为了在不发生优质基因损失的情况下产生新的个体。本文主要采用部分映射交叉PMX。具体步骤如下：

步骤1：随机选择并交换父代的基因片段；

步骤2：找到步骤1基因片段的映射关系；

步骤3：根据步骤2的映射关系合法化子代。

以n=6的流水车间调度为例，PMX如图3所示，其中父代1选择的基因片段为6、2、4；对应的父代2选择的基因片段为2、1、3；基因片段的映射关系为6对应1，4对应3。

图3 PMX示例

为了避免陷入局部最优解，应该使用变异算子来增加交叉后种群的多样性。本文应用两点交换变异算子。交叉操作和变异操作协同完成搜索空间的全局搜索和局部搜索。

2.4 禁忌搜索

在FSP-CTW中，由于作息时间的存在，工件的加工可能在不同的工作时段，而工作时段之间存在休息时段，因此可能不存在完整的关键路径，为提高搜索效率，在原有算法的基础上加入了禁忌搜索，防止在搜索过程中陷入局部最优的同时还可以搜索更多解空间。具体流程如图4所示。

图4 算法流程图

在车间调度问题的求解中，常用的禁忌搜索方法是插入式方法，即将工件插入到其他工件之间加工。将搜索方式分为3种：向前插入，向后插入，交换。搜索方式与任意两道工序结合构成禁忌表。比如，以图2的编码为例，禁忌搜索表为{1,5，“1”}，则表示将工件5插入到工件1之前，即工件5的加工在工件1之前，示例及结果如图5所示。

图5 禁忌搜索示例

3 案例仿真与分析

为方便研究FSP-CTW，设计15个案例，工件数量10～100，机器数量5～20，加工时间服从1～100的均匀分布，加工时间单位为min。将调度起始日期设置为2020年7月6日，工作制、工作时段均设置为5 0 1 2 3 4 8 2 4 1 4 -1，即均为5天工作制，每个工作日的调度起始时刻为8 h，则每个工作日的工作时段为8 h～12 h，13 h～17 h。

实验设计如表2所示，其中A组不考虑作息时间，B组中工件加工均可恢复，可采取直接映射的策略，即将调度方案直接应用在FSP-CTW模型中，并重新解码，C组中工件加工均不可恢复，采取两阶段优化策略，即在第一阶段不考虑作息时间，第二阶段考虑作息时间并将第一阶段的调度方案作为初始调度方案，进行再优化。

表2 实验设计

A、B组以及C组第一阶段的算法参数设置为种群规模为200，交叉概率为0.80，变异概率为0.05，最大迭代次数为150。C组中第二阶段的算法参数将最大迭代次数设置为60，最大值滞留代数设置为20。每个案例各运行10次，实验结果如表3所示，其中L表示总工序数量，A～C列的值表示算法的最优结果，表示2020年7月6日至调度最大完成时刻的时间，时间单位为min。

表3 实验结果

从实验结果可以看出A、B、C三组的最优结果存在C>B>A的关系，表明作息时间的存在、加工可恢复与加工不可恢复均对调度目标存在影响。A组中，Case1、Case2的结果最为集中，其在B组中的结果最为集中，表明采用的算法具有较好的效果。结合单因素分析方法，通过对比分析作息时间的存在、加工可恢复与加工不可恢复均对调度目标的影响。对比组合为A-B、A-C与B-C，显著性水平设置为0.05，分析结果p值均小于0.05，表明作息时间的存在、加工可恢复与加工不可恢复均对调度目标存在显著影响。因此，在调度中有必要考虑休息时段和考虑工件加工是否恢复。其中Case9的A-C组最优结果的甘特图分别如图6～图8所示。

图6 Case9的A组最优甘特图

图7 Case9的B组最优甘特图

图8 Case9的C组最优甘特图

由表3可知，Case9的A-C组最优结果分别为4280、15 380与16 727，分别对应2020年7月8日23时20分、2020年7月16日16时20分与2020年7月17日14时47分，与图6～图8吻合。当加工可恢复时，一些工序跨越了休息时间段，而加工不可恢复时，工序均不可跨越休息时间段，仅被安排在工作时段内，验证了算法的正确性。