基于混合算法的七轴机器人逆解求解*

杨 康，熊瑞平，潘楚光，卢文翔，徐毅松

(四川大学机械工程学院，成都 610065)

0 引言

机器手逆运动学是指通过给定的机器手末端位置位姿求得机器手的各个旋转轴角度。运动学逆解求解是机器人学的核心，对于机器手避障、克服奇点、提高机械臂灵活性等有极大用处[1]。

机器手逆解求解一般分为解析法与数值迭代法。解析法在求解多轴机器人时较为复杂，一般在特定结构机器人逆解求解时使用。数值迭代法是将机器手逆运动学问题转化成数学迭代优化的过程，进行一步步接近最终结果从而达到最终姿态。DULEBA等[2]利用雅各比伪逆矩阵进行了机器手运动学逆解的求解。CHIRIKJIAN等[3]利用离散性微分方程来进行求解机器人雅各比伪逆矩阵，简化了运算步骤。何理等[4]利用SVD分解求广义逆来避免机器手运动过程中的奇异性问题，同时简化了雅各比矩阵。杨扬[5]建立了基于运动轨迹的约束泛函，优化了冗余机器人的逆解。

近年来智能算法也越来越应用在机器手求逆解的过程中，进一步提高了机器手的工作精度。石建平[6]通过粒子群优化算法进行了平面冗余机器人的运动学逆解求解，获得了更快的收敛速度与更好的收敛质量。刘洋[7]通过多目标粒子群算法实现了机器人位置精度与姿态精度的控制，极大的满足了实际应用的需求。李国江等[8]利用多种群协同进化算法进行了绳索牵引并联机器人末端位置补偿，提高了末端位置的精度。吉阳珍等[9]利用组合优化算法用于逆运动学求解，提高了精度以及稳定性。郑雪芳等[10]基于改进萤火虫算法进行了冗余机器人的轨迹规划。

由于数值解求解过程中存在累积误差，且会陷入局部最优的状态，智能优化算法又存在搜索范围广，搜索速度慢的问题，所以本文采取先用数值迭代法求出最接近期望位姿的机器手初步最优角度解，再利用粒子群优化算法在初步最优角度解处偏置±10°进一步搜索优化，提高机器手逆解精度与准确度。

1 机器手迭代法

1.1 机器手逆运动学模型

本文以自由度为6的七轴机器人为主要研究对象，根据DH方法建立机器手模型，机器手的DH参数如表1所示。

表1 七轴机器人DH参数

长度ai(i=1,2,…,7)是指Xi-1轴从Zi-1轴移动到Zi轴的距离，扭角αi是沿Xi-1轴从Zi-1轴转动到Zi-1轴的角度，偏置di是沿Zi轴从Xi-1轴移动到Xi的距离，关节角θi是沿Zi轴从Xi-1轴转动到Xi轴的角度[1]。

由机器手运动学知识得到，根据DH参数[θαda]可以得出从坐标系Xi-1Yi-1Zi-1到坐标系XiYiZi的变换关系为：

(1)

将七轴机器人的7个旋转矩阵从左到右依次相乘，能得到机器手末端坐标系相对于基坐标系的位姿矩阵：

(2)

式(2)表示机器手的末端位姿方程，矩阵R3×3、P分别表示机器手末端的位姿矩阵及位置矩阵，位姿矩阵表示机器手末端分别沿着X、Y、Z方向旋转角度的3个自由度，位置矩阵代表着机器手的位置X、Y、Z位置坐标。

1.2 机器手逆运动学分析函数

数值法求解思想是将机器手位姿求解过程转化为牛顿迭代过程，每一步计算变化角度，一步步逼近最终结果。

机器手末端的位姿X由机器手位置x、y、z及末端绕x、y、z分别旋转的角度θ、α、γ来确定。

(3)

X=f(q)

(4)

(5)

(6)

∴

f(q)=f(q0)+J×(q-q0)+δ(q0)

(7)

f(q)-f(q0)=J×Δq+δ(q0)

(8)

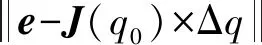
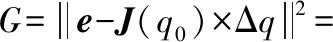
(9)

当

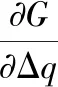
(10)

此时，当机器手的变化角度为Δq时，此时误差最小，并且伪逆矩阵可以消除机器手在运动过程中产生的奇异性影响。

本文数值法利用伪逆矩阵，通过机器手期待的末端位姿来计算机器手每次的迭代角度变化。

步骤1：设置机器手的初始位姿矩阵TF或者初始角度q，以及期望的终端位姿TL，初始化迭代次数i=0，最大迭代次数il=300，设定迭代收敛条件位置及位姿误差范数G，以及范数影响因子λ；

步骤2：计算出下一步机器手的变化角度Δq=JT(JJT)-1e；

步骤3：更新机器手各个旋转轴角度qc=qc+Δq；

步骤4：更新(qc)，得到机器手角度变化后末端位置坐标及绕X、Y、Z轴旋转角度；

步骤5：计算机器手此时的雅各比矩阵J(qc)；

步骤6：期望末端位姿t=[xyzθαβ]，T中各元素分别表示位置x、y、z及绕三坐标轴旋转的角度θ、α、γ，计算末端位姿与此时的位姿之间的误差e=t-f(qc)；

步骤7：迭代次数i=i+1;

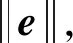
2 粒子群算法

2.1 基本原理

粒子群算法是模仿鸟群觅食的模型进行修正优化得到的算法，通过一个由m个粒子组成的群体在D维搜索空间中以一定的速度飞行，每个粒子在搜索时，考虑到了自己搜索到的历史最好点和群体内其它粒子的历史最好点，在此基础上进行位置与速度的变化直到到达历史最好点[11-12]。

2.2 算法流程

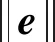
粒子群算法位置与速度的关系：

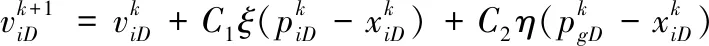
(11)

基本粒子算法步骤：

步骤1：随机初始化粒子群，包括随机位置和速度；

步骤2：计算每个粒子的适应值[13]；

步骤3：对于每个粒子，进行比较每次迭代后的适应值并且提取粒子更优的适应值，提取历史最优值；

步骤4：判断其是否满足迭代停止规则，若满足，跳出算法循环输出结果。否则进行位置与速度更新，转到第2步[10]。

2.3 适应度函数

机器手的运动特性包括位置坐标X、Y、Z与位姿即绕X、Y、Z三轴旋转的角度θ、α、γ，本文算法的适应度函数是机器手位姿误差范数大小比较，寻求机器手误差最小值。

通过机器手期望的位姿旋转矩阵计算得到机器手末端位姿

t=[XL、YL、ZL、θL、αL、γL]

(12)

粒子群算法迭代过程中通过在初始范围内搜索变化的角度，通过计算产生的机器手末端位姿

f(qc)=[XP、YP、ZP、θP、αP、γP]

(13)

评价函数：

(14)

式中，G表示机器手期望中的位姿误差与实际中的位姿误差范数。

3 数值迭代法与粒子群算法混合算法

冗余机器手由于机器手旋转轴数目更多，逆运动学解数目是无穷的，所以本质上是一个多元多峰函数最优解的求取问题，其适应度函数是一个带约束条件的复杂的方程组，计算量较大，若是直接利用粒子群算法在全局范围内进行角度搜索，搜索角度范围太大，计算量繁重，收敛速度更慢精度不高，消耗算力也更多，且容易陷入局部最优的范围解内。

数值法迭代优势在于迭代速度很快，程序简单，目标明确能够短时间内达到一个接近终点的目标，但是由于需要利用到雅各比矩阵，在计算每次变化角度时省略了后面很多较小量级的角度，所以机器手每次迭代都存在较大的迭代累积误差，且容易陷入局部循环的境地。

本文将数值法与粒子群算法相结合起来，先用数值法迭代进行初步计算，得到七轴机器人的初步旋转角度，然后利用粒子群算法进行进一步搜索，搜索范围在初步解上，每个轴偏转10°，优化精确机器手的位姿，此时消除了数值解过程中式(8)中δ(q0)产生的累积误差，又简化了粒子群算法的搜索范围，降低了搜索成本，加快了搜索迭代收敛速度，因此很大程度上能够搜索到较为精确的机器手逆解。

混合算法求机器手逆解的过程大概如下：

步骤1：输入机器手DH参数，运用MATLAB工具箱创建七轴机器手；

步骤2：输入机器手期望的终点末端位姿旋转矩阵TL以及起点位姿或者起始角度等；

步骤4：初始化粒子群初始角度范围θmax=[θ1+10°,θ2+10°,θ3+10°,θ4+10°,θ5+10°,θ6+10°,θ7+10°],θmin=[θ1-10°,θ2-10°,θ3-10°,θ4-10°,θ5-10°,θ6-10°,θ7-10°]在这个角度范围内随机初始化角度粒子及相关粒子群参数；

步骤5：将粒子带入粒子群算法求解机器人运动学逆解；

步骤6：输出机器手逆解结果θ，逆运动学求解结束。

进行数值迭代法初步迭代后，得到初步的机器手角度以及初步的位姿范数误差，再在此基础上初始化粒子群角度范围进行粒子群算法迭代得到进一步的精确解并得到此时的位姿范数误差，比较初步迭代后与粒子群算法优化后的结果。

4 实验结果

经过指定机器手的初始点位姿与期望的终点位姿，根据数值迭代与粒子群混合算法步骤进行仿真求解，如表2所示实验初步设置的初始位置位姿与期望的初始位置位姿；如表3所示机器手进行初步迭代后的角度初步最优解与初步误差，误差范数等；如表4所示混合优化算法运行完毕的角度解以及此时的位置位姿误差与误差范数。

表2 初始位姿与期望位姿设置

表3 数值解初步求解后结果

表4 混合优化后实验结果

从表格中相关的实验数据可以看出，经过数值迭代法初步计算后的初步结果，初步迭代后的位姿误差较大，且结果误差始终无法进一步减小，在此角度基础上偏置±10°，缩小搜索角度范围，进行PSO算法搜索优化后，误差明显大大减小。

小结：在整个混合优化算法求解机器手逆解过程中，机器手逆解进行了二次精度优化，在初步数值迭代法计算步骤中，机器手容易产生累积误差，当累积误差到达一定程度时，位姿误差很难降低到一个理想数值，在初步最优角度解的基础上偏置±10°利用PSO算法进行搜索，搜索结果显示位姿误差大大降低，降低了数值迭代法运行过程中存在的累积误差状况，同时搜索范围的降低使得迭代收敛速度提高，逆解精度大大提高。

连续轨迹测试：

根据设定的七轴机器人初始角度θα=[0,pi/6,-pi/18,pi/3,pi/5,0,-pi/6]及混合优化算法优化过后的终点角度θβ=[0.31,0,1.04,-1.57,0.17,0.26,0.21]，在这两个位姿间利用机器人工具箱插值10次，随后利用样条曲线得到机器人运动过程中的角度值结果如图1所示，以及运行过程中机器手的位姿变化如图2所示，位姿误差范数如图3所示。

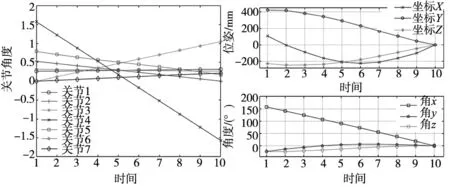
图1 机器手轨迹角度变化 图2 机器手轨迹位姿误差变化

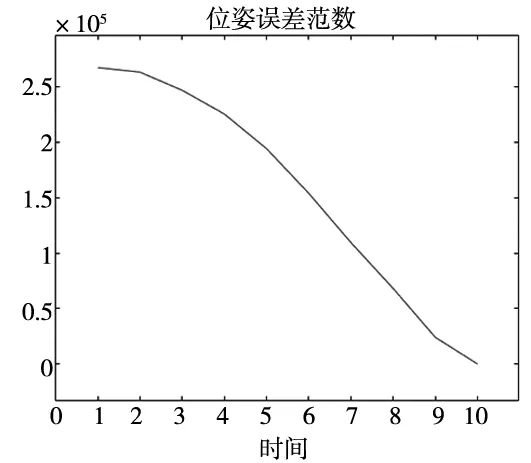
图3 机器手轨迹位姿误差范数

分析实验数据，七轴机器手在进行数值迭代法求逆解时，会产生累积误差导致最终结果不能降低到一个理想的位置，在初步迭代结果上，选取位姿误差最小时的角度解，在此角度基础上偏置±10°进行二次优化搜索，减小了粒子群的搜索角度范围，加快了搜索速度，加快了迭代收敛速度，极大地提高了计算精度，同时在后续的轨迹规划中，利用插值的思想，机器手的角度变化波动较为平滑，同时位姿误差以及位姿误差范数收敛性很强，机器手的运动更加平稳，无较大波动，冲击较小，因此混合优化算法具有极强的利用研究价值。

5 结论

本文在分析了数值迭代法与粒子群算法在冗余机器人求逆解过程中的弊端后，提出了一种混合优化算法，先利用数值迭代法接近末端执行器期望的末端位姿，缩小搜索范围，在迭代过程中提取出位姿误差最小时的角度值，然后在此角度范围偏置±10°，减小搜索范围，进行粒子群智能优化算法的搜索，进一步逼近结果，得到机器手优化后的角度后，在后续的轨迹测试中，利用最终优化结果与初始角度进行插值计算，机器手的角度变化更加柔和，波动更小，同时位姿误差与位姿误差范数的波动收敛性更强，机器手的运动更加平稳，冲击更小。实验论证大大提高了机器手末端的位姿精度，提高了机器手在运动过程中的平稳性，在实际的研究过程中具有极大的研究价值。