改进果蝇算法求解零空闲流水车间调度问题*

2022-03-04尹瑞雪冯旭青李付春

组合机床与自动化加工技术 2022年2期

尹瑞雪，冯旭青，吴拓，李付春，王泽

(贵州大学机械工程学院，贵阳 550025)

0 引言

零空闲流水车间调度问题(NIFS)具有很强的工业背景，广泛见于集成电路、纺织、玻璃和陶器等产品的生产制造过程中。基于成本及加工工艺要求的考虑，要求每台机器一旦开始加工某个工件，则需要不间断的把所有工作都加工完成，不允许机器操作之间有空闲时间，即机器不能空转。

实现零空闲车间调度将有效节约机床闲置能耗，是实现机加工行业节能减排的有效途径之一。因此，针对该问题，国内外学者展开了一系列研究。BAPTISTE等[1]证明了F/no-idle/Cmax是一个NP难问题。武磊等[2]求解以总流经时间和最大完工时间为目标的零空闲流水线调度问题，改进了和声搜索算法的求解模型。王亚敏等[3]以E/T指标最优为优化测度，提出了一种蛙跳求解算法。潘全科等[4]基于PSO算法，提出了离散粒子群算法求解NIFS问题。李丽娟等[5]则改进了标准觅食算法，引入交叉优化算子、混合复制策略及自适应迁徙概率求解问题。研究表明，采用更有效更稳定的优化算法是获得最优解的重要前提。

针对该优化问题，本文拟采用果蝇优化算法(fruit fly optimization algorithm，FOA)[6]，该算法是一种新的基于果蝇觅食行为寻找全局最优解的新方法。该算法操作简单，易于实现，具有较好的局部搜索能力[7]。已有的研究中，仅有少数学者采用该算法解决此类优化问题。杜利珍等[8]针对不相关并行机混合流水车间调度问题，利用权重系数来提高算法的随机搜索能力。高兵新[9]将果蝇算法应用于炼钢-连铸生产中，并设计动态搜索半径求解NIFS问题。以上这些已有的少量研究大多采用的是传统果蝇算法，其具有局部最优的局限性，且寻优后期可能存在收敛速度慢、寻优精度低的问题。因此，本文提出了一种改进的果蝇算法用于解决该优化问题，该算法针对种群初始化、嗅觉搜索方式、视觉觅食阶段飞行方式等方面均进行了改进，不仅设置了多个种群中心，并在嗅觉搜索阶段加入破坏重建，多重独立交换、插入领域搜索及随机权重系数变换；在视觉觅食阶段引入免疫算法激励度对传统果蝇算法做出了改进，使搜索能力达到进一步增强；最后，通过案例验证，证明该算法能有效提高全局寻优效果，其稳定性也有所改善。

1 问题描述与数学建模

零空闲车间调度，即每台机器上的两个连续操作之间不允许有空闲时间，工件加工一旦开始，不允许中断。为了满足零空闲约束即每台机器一旦开启，就必须连续切削直至把所有工件加工完毕。NIFS问题可描述如下：有n个工件的集合N={1,2,…,n}，m台机器的集合为M={M1,M2,…,Mm}。工件在零时刻都可用，且必须按照相同的工艺路线次依次经过机器M1、M2直到机床Mm。pij为工件i(i=1,2,…,n)在机器Mj(j=1,2,…,m)上的加工时间(s)。每个工件在任意时刻最多只能被一台机器加工，且每台机床最多只能加工一个工件。其调度目标就是通过安排工件的生产次序，以达到最大完工时间最小化。

在建立该调度问题数学模型的过程中，一个工件的加工排列可用π=(π(1),π(2),…,π(n))表示，即工件按π(1)到π(n)的顺序依次加工；相邻的机器j和j+1之间存在的开工时间差记为Ej,j+1(π)，pπ(i),j表示工件在π(i)位置上的加工时间，具体计算方法如式(1)所示；加工排列π对应的最大完工时间(s)记为Cmax(π)，故某个具有加工排列π的工件的最大完工时间可用式(2)进行计算。

(1)

(2)

用A表示具有不同工件生产次序的调度方案的集合，则NIFS问题的目标是在集合A中找到一个最优的调度方案A*，使A*得的总完工时间在集合A中最小，即调度A*的最大完工时间小于其它具有不同工件生产次序的调度方案的最大完工时间，如式(3)所示。

Cmax(A*)≤Cmax(A) ∀A*∈A

(3)

式中，Cmax(A*)和Cmax(A)分别为调度方案A*与集合A对应的完工时间。

2 问题求解

本文拟采用改进果蝇算法进行求解。传统果蝇算法独特的嗅觉与视觉搜索特性使其原理易懂、易于实现，并且具有较强的局部搜索能力，但其全局搜索能力相对较弱，容易陷入局部最优，进而早熟收敛[10]。

改进果蝇算法在传统果蝇算法基础上，建立了多种群中心搜索模式，改进嗅觉搜索方式，引入破坏重建、插入领域局部搜索；并将免疫算法激励度引入果蝇视觉觅食阶段。首先，编码和解码将使用矩阵来表示，采用1×n的矩阵π=[a11,a12,…,a1n]表示一个个体的编码，其中n为工件的个数。用元素a1j(j=1,2,…,n)表示矩阵π=[a11,a12,…,a1n]中的任意一个工件，将其按照a11～a1n的顺序依次进行加工；此外，设置多个种群中心来提高全局搜索能力。种群中心位置采用随机生成的方式产生，种群中心数目为Csize，种群规模为Psize。

(1)嗅觉搜索

在嗅觉搜索阶段，从种群中心出发，在中心果蝇产生其他果蝇个体。为了改进基本果蝇算法给予的随机方向和距离的方式，本文采用多阶段方法进行搜索，主要分为以下三个阶段：

第一阶段：在迭代次数小于给定迭代次数D时，半数果蝇个体引入IG算法[11]的破坏与重建过程产生个体位置，剩余果蝇个体数减1的位置采用多重领域交换结构产生。

IG算法的破坏与重建过程中，首先随机从排列πa中删除d个工件进行破坏，并将这d个工件构成排列πd；接着从πd中取出第一个工件并插入到πa的可能位置，根据目标函数来评估得到的部分序列的插入位置的好坏，选择最优的部分序列进入下一代迭代；然后再取出第二个工件插入到最优的部分序列中，依次迭代，直到πd中所有工件取出完毕进行重建。

采用多重独立交换结构对领域作搜索，是在排列中随机选择两个位置的工件，然后交换这两个工件。评估交换后的排列的适应度值，若交换后的适应度值比当前解好，则更新当前解并替换之前的排列，然后继续选择位置，交换工件，重复上述操作，直达操作次数达到阈值M为止。

第二阶段：当迭代次数大于等于给定迭代次数D时，所有果蝇个体位置用随机权重系数变换产生以增强后期跳出局部最优的能力。

第三阶段：因为中心果蝇相对上一代果蝇位置占优，故对此插入局部的领域进行不断的搜索，将得到的优势个体放入种群。

插入领域的局部搜索是对于排列πa，依次取πa(1),πa(2),…,πa(n)。首先取出πa(1)插入到πa-πa(1)排列的所有可能位置，得到最优排列；然后取出πa(2)，重复上述操作直到取尽所有工件，得到最终的最优排列后替换原排列πa的位置。

整个嗅觉搜索过程流程图如图1所示。

图1 整个嗅觉过程流程图

(2)视觉觅食

在视觉觅食阶段，果蝇个体会根据味道浓度找出最优的个体位置并替换种群中心的位置，并利用视觉引导种群飞向新的种群中心。若此时的最优个体不是全局最优个体，则易导致算法陷入局部收敛的困境；然而免疫算法具有自身产生多样性和维持机制的特点，可以有效保持种群多样性，避免寻优过程中的早熟现象[11]。结合二者的特点，本文将在免疫反应过程中，将用于衡量抗体最终质量的激励度引入果蝇算法，以提高算法稳定性，增强寻优能力。

果蝇算法中的果蝇个体对应于免疫算法中的抗体，食物对应于免疫算法中的抗原，味道浓度对应于表征免疫细胞与抗原结合强度的亲和度评价算子。相关定义如下：

①抗体与抗原之间的亲和度评价定义为目标函数的倒数，即果蝇个体适应度值的倒数，可表示为式(4)：

(4)

式中，Cmax(πa)为排列πa的最大完工时间。

②抗体与抗体之间的亲和度代表了两个抗体之间相似程度，可表示为式(5)：

(5)

式中，πa,k=πb,k时，∂k=1，否则∂k=0；πa,k和πb,k分别为抗体a的第k位和抗体b的第k位的数值；n为工件的数量，即抗体或果蝇个体编码大小。

③抗体浓度与抗体种群的多样性相对应，可表示为式(6)：

(6)

式中，aff(πa,πb)>δs时，S(πa,πb)=1，否则S(πa,πb)=0；δs为相似度阈值。

④抗体激励度的计算方法为式(7)：

(7)

式中，sim(πa)为抗体πa的激励度，exc(πa)=1/den(πa)；ps为多样性评价因子；由式(7)可以看出，激励度sim(πa)随果蝇个体适应度值f(πa)的增大而增大，随抗体浓度值den(πa)的增大而减小。

果蝇视觉觅食阶段引入免疫算法激励度后的具体操作为：首先评估每个种群个体的激励度；随后选择一定比例λ的种群飞向以适应度大小排序的种群中心，而剩余的种群则飞向以激励度大小排序的种群中心，最终获得新的种群中心群。

整个视觉觅食过程流程图如图2所示。

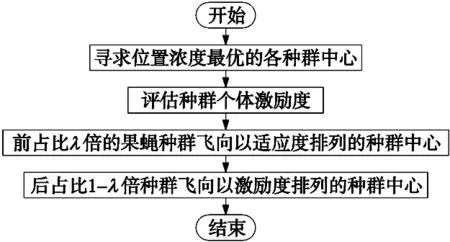
图2 整个视觉觅食过程流程图

3 算例试验

3.1 有效性分析

以平均性能参数ARI作为评价因子，ARI的值越大，算法的性能越好，其计算式如式(8)所示。其中，Ci表示算法第i次运行的结果值。

(8)

表1 算法比较结果

通过分析表1可知：

①IAFOA算法在50×5规模问题下求得的最优解相较于IBFO_NEH算法相同；说明二者求解该问题时性能相近；此外，IAFOA在其余5个规模问题下的求解结果均明显优于其余两种算法，这表明求解零空闲流水车间调度问题时，改进的果蝇算法是有效可行的。

②运用IAFOA算法相比较IBFO_NEH 算法在平均性能参数ARI上均有所提高，IAFOA算法在最好情况下的ARI值为9.64%，最低为0.37%，体现了改进果蝇算法的全局寻优的良好性能。

3.2 算法改进元素对比分析

采用平均相对偏差(average percent relative deviation，APRD)和标准差(stand deviation，SD)[14]来衡量算法特性，二者的计算方法参照文献[14]。APRD用于衡量算法搜索的最优解与当前最优解的平均相对偏差百分比，体现算法的平均寻优精度，其值越小平均寻优精度越高；SD用于衡量相对偏差百分比的平均离散程度，体现算法的稳定性，其值越小算法稳定性越好。借助MATLAB软件对Taillard算例中前6个规模的第2个算例进行求解，设置具体参数为：种群中心数目为Csize=10；种群规模Psize=50；迭代次数Maxgen=40；多样性评价因子ps=0.3；种群比例λ=0.5；相似度阈值δs=0.1n；各算例随机运行次数Nr=10。

将本文提出的改进果蝇算法记为IAFOA；在此基础上，将仅不采用插入领域的局部搜索的算法记为IAFOA1；仅不采用破坏与重建过程的算法记为IAFOA2。将上述两种方法都不采用的算法记为FOAS；基于FOAS，在视觉觅食阶段采用传统的飞行方法，即果蝇全部飞向最优的个体位置的算法记为FOAF。经过对比分析，各改进元素对比结果如表2所示。

表2 各改进元素的对比结果

通过对比表2中FOAF与FOAS的结果可知：

①FOAS的平均相对偏差的平均值相比FOAF要高0.14，说明FOAS算法相比较于FOAF，平均寻优精度要差一点，算法搜索最优解和当前最优解存在一定偏差。

②从SD值来看，FOAS在50×5、50×20规模问题下的SD值比同等问题下FOAF稍大，但在其余四个规模问题下的SD均小于采用传统飞行方式的FOAF算法，并且FOAS的平均标准差比FOAF要低0.044，这些结果表明 FOAS算法的稳定性更高。总的来说，在视觉觅食阶段加入作为种群中心飞行引导的免疫算法激励度，算法稳定性会有所提升。

通过对比表2中FOAS与IAFOA1、IAFOA2和IAFOA的结果可知：

①IAFOA1和IAFOA2、IAFOA相较FOAS，在APRD值上均有所提高，分别提高了1.368、0.633和1.391。这表明在嗅觉搜索阶段加入破坏与重建过程和对种群中心进行插入领域的局部搜索策略会使算法平均寻优精度稍有降低，但这会有助于跳出局部最优的困境，增强算法的全局寻优能力；以上三种方法的平均SD值相较FOAS更小，分别降低了0.32、0.146和0.332，这些结果表明了三种算法平均离散程度更小，算法更稳定。

②在IAFOA1和IAFOA2、IAFOA三种方法中，可以看出三种算法在求解50×5问题的SD为0，在求解其余5个规模问题时出现一定的波动；对比不同规模问题的求解结果可知，IAFOA2波动较大；此外，IAFOA2的平均APRD最优且与IAFOA1相差不大，但稳定性相较于其余二者有所降低。总的来说，加入破坏与重建过程相对于插入领域的方法更为重要，表明破坏与重建过程会对算法寻优精度有所影响，但能较好的改善算法稳定性。

③通过对比不同改进元素算法的平均值可知，IAFOA的稳定性优于其他算法，平均寻优精度稍低，全局寻优能力有所改善。其中，IAFOA与IAFOA1对相同规模的算例，APRD与SD值相近。这表明两种算法具有相互的优势，算法之间的差别并不会有很大影响。而IAFOA2与上面两种算法相比，表明了破坏与重建过程对于求解零空闲流水车间调度中的改进果蝇算法的寻优精度和稳定性有更大的权重。