基于无监督学习的岸边集装箱起重机关键部件故障诊断方法*

张 氢 李帅杭 陈 星 肖炳林 李 恒

1同济大学机械与能源工程学院 上海 201804 2海南省锅炉压力容器与特种设备检验所 海口 570203

3广州港股份有限公司南沙集装箱码头分公司 广州 510100

0 引言

海洋运输是最主要的国际物流运输方式，它承担了我国进出口货运总量的90%。岸边集装箱起重机（以下简称岸桥）是整个码头完成货物从海洋到陆地转移的核心装备。为防止岸桥发生故障导致的码头效率降低、停工，甚至人员安全事故，针对岸桥的故障检测是十分必要的。如今，我国的集装箱码头正在陆续进行智能化改造，同时建设新的自动化、智能化码头。

目前，对齿轮箱的故障诊断研究正在飞速发展，针对齿轮箱振动数据的诊断方法较多[1-3]。然而这些方法大耗费时间较长，需要额外设计诊断模型的自我更新等问题。在对齿轮箱的无监督故障诊断领域中，现有的研究并不多。Luo J等[4]提出了一种基于流形学习和支持向量机的半监督学习方法，通过少量的标记样本训练，从行星齿轮箱试验台中获取数据，实验验证了其方法的有效性。Cheng G等[5]将从EMD分解后获得的能量特征值作为无监督的SOM网络的数据输入，进行故障分类，实验证明该方法能够准确地提取和区分这些信号的故障特征。李状[6]利用C均值聚类算法对ART2神经网络的分类性能进行了优化，在风电机组齿轮箱的实机信号上成功进行了无监督的故障诊断。这些方法能够在试验台数据或运行较为稳定的风机齿轮箱中获得较好的诊断结果，但岸桥齿轮箱的工况更加复杂、存在大量的加速减速和正反转运动，使得其故障诊断尤其是无监督的故障诊断难度增大。在基于岸桥齿轮箱的大数据故障检测中，遇到的很大的问题是故障数据缺失，无法训练，也无法自行学习更新。

本文提出了一种基于无监督机器学习的岸桥齿轮箱故障检测方法。通过对岸桥的振动信号进行处理，提取能够反应其状态的特征值，然后通过无监督的机器学习方法判断齿轮箱的健康状态。

1 振动信号的特征值

在对信号进行聚类分析前，首先要明确聚类的对象，性能良好的对象应该能够表征当前信号的数据模式，这些数据模式不应受到转速、载荷等其他因素的影响，能够正确区分正常模式的数据与故障模式的数据。此外，为了减少无监督聚类的训练时间，聚类对象需要尽可能的正交，即去除冗余的特征值，保留下能够充分表征当前信号的特征值。

1.1 特征值提取

实际中采集到的振动信号为一段随机的离散信号，为了反映该段信号的振动模式，以该段信号的统计特征值作为表征该信号的特征值。振动信号的统计特征值可分为两类，时域统计特征值与频域统计特征值。

本文采用的时域统计特征值包括均值、标准差、均方根值(有效值)、峰值指标、脉冲指标、波形指标、峭度指标、偏度指标、裕度指标等。其中标准差反映了信号围绕均值的波动程度，描述了信号的波动分量；均方根值描述了振动信号的能量，稳定性好，重复性好；峰值指标和脉冲指标可用来检测信号中是否存在冲击；峭度指标对信号的冲击特征很敏感，当数值过大时，表明机械中可能存在由于间隙过大、滑动副表面存在破损等原因导致的冲击性振动；裕度指标可用于检测机械设备的磨损情况；偏度指标反映振动信号的非对称性。

频域统计特征包括功率谱重心指标、均方谱、功率谱方差、相关因子、谐波因子、谱原点矩等。功率谱是反映单位频带内信号功率随频率的变化情况，也就是信号功率在频域内的分布情况。功率被定义成幅值的平方的时间平均分量，而这个过程也可以看做是去除频域谐波分量的相位信息的过程。功率谱重心指标反映了能量重心位置的变化程度，可以较好地描述信号频域特征的变化；功率谱方差反映了能量分布的离散程度；功率谱均方频率表征功率谱主频带的位置；相关因子反映了谱能量分布的相关程度；谐波因子反映了谱的分布状态和谱宽情况；谱原点矩反映功率谱的总体能量情况。

这些时域、频域特征值能够较好地反映机械设备在故障状态与非故障状态下的差异[7,8]，选择其构成的特征矩阵作为机器学习的对象。

1.2 特征值归一化

不同的特征值之间存在较大的数量级差异，需通过各特征值归一化来避免某一较大的特征值占据主导地位。

Z-Score标准化既适用于数值比较集中的情况也适用于数值分散的情况，且能保证归一化结果相对稳定。此外，Z-Score标准化在分类、聚类算法中或者使用PCA等技术进行降维时，其性能表现较好，故本文选用Z-Score标准化。

Z-Score标准化后数据符合标准正态分布，即均值为0，标准差为1，其转化函数为

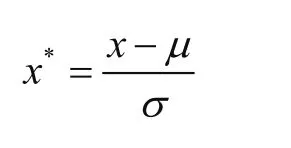
式中：μ为所有样本数据的均值，σ为所有样本数据的标准差。

1.3 特征值降维

因为各特征值之间可能存在信息重叠，为了提升机器学习的效率，减少不必要的计算量，在提取了上述信号特征之后需要对特征值进行降维，本文采用主成分分析法（PCA）对特征进行降维，利用正交变换来对一系列可能相关的变量的观测值进行线性变换，从而投影为一系列线性不相关变量的值，这些不相关变量称为主成分。

求解归一化后的特征值矩阵的协方差矩阵，再求出其协方差矩阵的特征值，就可以得到各个成分的贡献率。贡献率表明主成分综合变量数据的能力，贡献率越大说明其综合原始变量数据的能力越强。一般选取排名靠前且累计贡献率大于80%的主成分。

2 无监督聚类

在有监督机器学习方法中，需要获取大量的有标签数据作为输入，具体到故障检测领域中，即需要大量的实际故障数据作为训练集与测试集。然而，目前在港口机械中，由于机型众多，机构组成复杂，工况各异，这些小样本的监督学习标签局限性比较大，同时这些标签数据由于历史原因又少，在效果上差强人意。

本文考虑使用无监督的方法进行岸桥的故障检测，目前常用的无监督方法主要有：K-Means、ART2网络、SOM网络等聚类方法。K-Means聚类作为一种启发式算法，极适用于大数据处理任务，目前已经在计算机视觉、天文学、故障诊断等领域取得成功应用。

2.1 K-Means聚类

K-Means算法源于信号处理中的一种向量量化方法，其聚类的目的是：把n个点划分到k个类别中，使得每个点都属于离他最近的均值对应的类别[9]。K-Means聚类的步骤为：

1）选取k个聚类中心，也称其为该类的质心。若完全随机选取质心，则可能使聚类过程计算量过大，增加不必要的迭代步骤。因此，在选择质心时需要增大距已选质心较远的点的被选中的概率。

2）对每个样本点i，计算其所属的类别

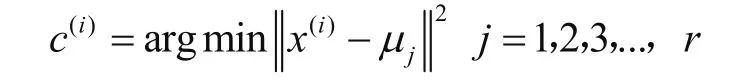
式中：x(i)为样本，μj为类的质心，c(i)为计算出的样本所属的新类，‖a－b‖2为计算两者间的欧几里得距离。

此步可具体分为计算距离与寻找新类2步，主要的计算量发生在距离计算中。为加快迭代聚类过程，通过elkan K-means算法，利用三角形的几何特性可减少大量的计算步骤。

3）对每个类别，重新计算其质心位置

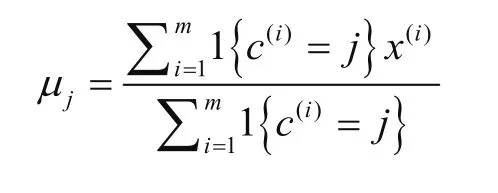
重复2）、3），直至收敛或达到终止条件。

损失函数为

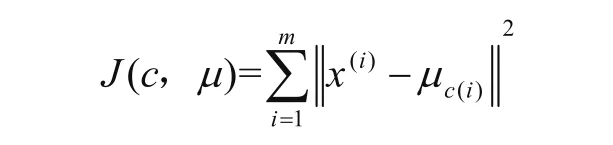
2.2 无监督机器学习流程

本文基于聚类的无监督故障诊断方法由3部分构成：对振动信号进行预处理得到特征矩阵；然后通过PCA算法对特征进行降维；最后通过K-Means算法对简化后的特征矩阵进行聚类。无监督故障诊断模型如图1所示。

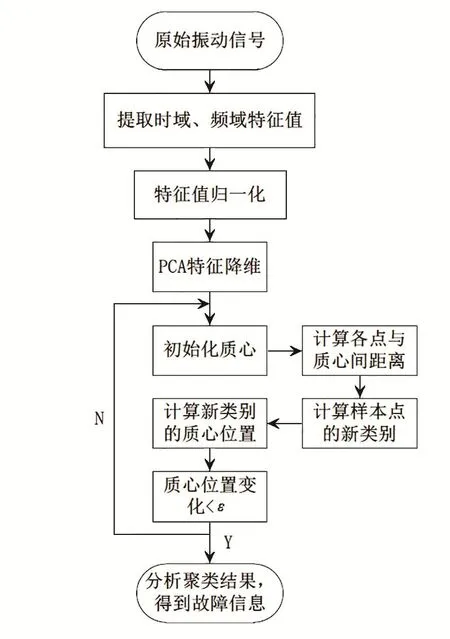
图1 无监督故障诊断模型

3 实际实验

3.1 实验1

采用某大学的公开数据集对本文提出的方法进行验证。该实验选择了安装有14 in的轴承在采样频率12 kHz下的驱动端数据，轴承存在内圈故障、滚动体故障、6点钟方向的外圈故障，转速为1 797 r/min。

从3组故障数据中各选出10条故障样本，再加上从3组对应的正常数据中各选出30条样本，组成总数90的数据集。

每条数据可计算出20维特征值，对特征值矩阵归一化后进行PCA主成分分析。为了便于可视化分析与展示，设置约简后的特征维数为3，可以计算出最终的3维特征值主成分贡献率之和为88.83%，认为能够表征原特征空间。

表1所示为某大学数据集中部分样本特征值示例，0～5为正常样本特征值，70～72为滚动体故障样本特征值，87～89为外圈故障样本特征值。对比表中各特征值可知，经过上述处理流程后，不同故障类型的样本能够明显区分开。

表1 各样本特征值

在对经过PCA后的特征矩阵进行聚类分析，设置聚类类别为4。通过K-Means算法将这90条数据分为4类，每类样本数分别为60、17、12、1。选取前2维特征值对聚类结果进行可视化，如图2所示。

图2 某大学数据集聚类结果

3.2 实验2

采用国内某码头岸桥设备的实机振动信号作为数据源。如图3所示，为岸桥起升机构的传感器安装示意图，共7个测点。

图3 传感器布置

起升机构上7个传感器的采样频率为51 200 Hz与25 600 Hz。电动机转速800～1 200 r/min，岸桥装卸集装箱质量范围为28～65 t。

当该岸桥出现异常时，将该时刻的数据添加到总数据集中，即可运用本文提出的无监督方法分辨出该异常数据。此次实验的数据集中包含示例岸桥的某一个时刻检测到的异常实际数据，后经停机拆箱检查后确认此为一轴承发生故障所致。

起重机原始数据中，各个测点间数据独立，文以单个岸桥的机构为分析对象，首先对原始数据进行整理，将机构的多测点数据整合为一条。

之后对振动数据进行特征值提取，得到特征矩阵。通过数据归一化消除特征值间的数量级差异，同时使得后续特征约简与聚类分析过程的性能得以提升。

将归一化后的特征值矩阵通过PCA进行降维，确定最终的特征维数为5。此时，各主成分贡献率之和为88.06%，表明约简后的特征仍能够较为全面的表征原始信号。

通过K-Means方法进行聚类分析，设置最终聚类类别为3，得到聚类结果后发现添加的故障数据被单独分为一类。选取前2维特征值对聚类结果进行可视化，如图4所示。实验证明本文提出的方法能够分辨出异常的岸桥振动数据。

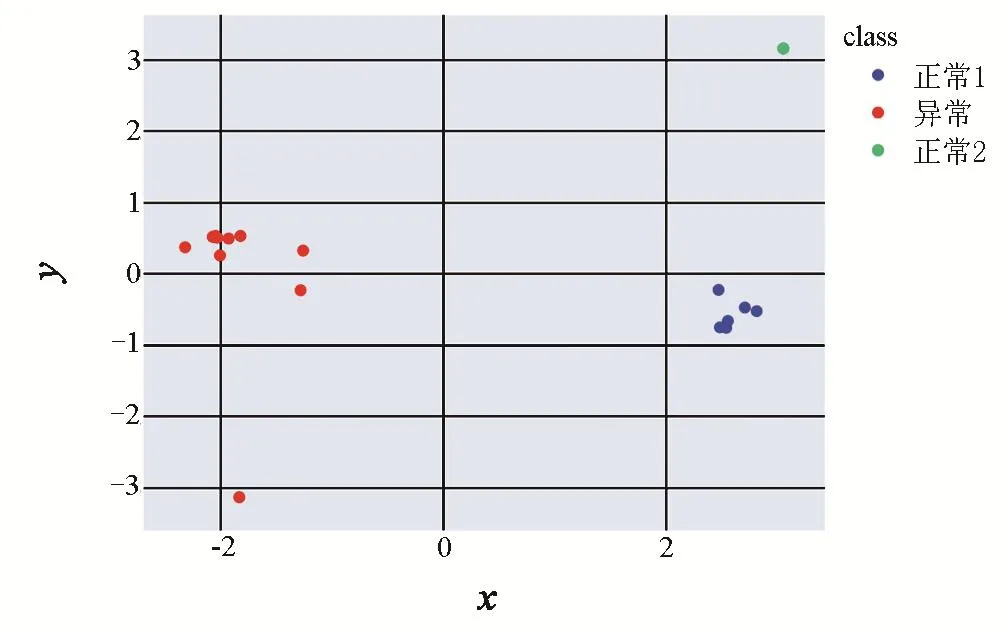
图4 岸桥实际振动数据聚类结果

4 结论

本文以港口中实际运行的岸桥为对象，进行了故障检测的研究。针对目前港机缺乏充足的故障标签数据的情况，提出了一种基于无监督方法的岸桥故障检测方法。通过提取反映设备当前状况的特征值，对其进行必要的归一化与降维，优化数据集，增强了下一步聚类分析的性能。通过实机检测到的数据进行验证，实验结果验证了该方法的有效性。