CSR上154 MeV/u C6+离子束分别入射Ti、V、Fe、Ni和Zn靶的X射线辐射

梅策香， 张小安， 周贤明， 曾利霞，梁昌慧

(1. 咸阳师范学院与中国科学院近代物理研究所联合共建离子束与光物理实验室， 咸阳 712000；2. 西北工业大学 超常条件材料物理与化学教育部重点实验室， 西安710049； 3.中国科学院近代物理研究所， 兰州 730000)

1 引 言

高电荷态离子与固体靶原子碰撞导致靶原子内壳层电子电离产生空穴，相应的空穴退激时伴随着发射X射线或俄歇电子[1, 2]. 精确测量离子与原子碰撞引起的靶原子内壳层电离截面，对研究原子内壳层过程以及建立合适的理论模型具有重要的意义，目前许多高科技应用领域需要精确的原子内壳层电离截面数据，例如材料元素分析中利用到的X射线荧光光谱技术[3, 4]、俄歇电子谱仪(AES)[5]以及聚变等离子体中的杂质诊断等，该研究成为倍受关注的热点领域之一[6-9].

离子与原子碰撞内壳层电离实验，早期主要集中于研究低原子序数的入射离子与靶相互作用过程中靶原子K壳层电子的电离问题[10, 11]；随着Si(Li)探测器分辨率的提高，研究逐步深入到L和M壳层电子的电离问题[12-14]. 与此同时，对离子激发原子内壳层电离的物理机制分析也迅速发展，相应的理论模型随之建立. 平面波玻恩近似(PWBA)[15]、两体碰撞近似(BEA)[16]和半经典近似(SCA)[17]可成功描述质子打靶引起的靶原子K壳层直接电离(DI)过程. 基于PWBA理论对入射能量损失、入射离子在靶核库仑中偏转、靶原子中电子受到的定态微扰中束缚能的增加、极化效应和相对论效应进行修正，建立起来的ECPSSR模型[18-20]，可较好的描述中低能轻离子的入射过程. 除直接电离外，入射离子通过俘获靶原子中的电子而使靶原子内壳层产生空穴(电子俘获)也是内壳层电离的主要机制之一. 一级波恩近似理论就是基于描述直接电离的平面波波恩近似和描述电子俘获的Oppenheimer-Brinkman-Kramers(OBK)公式联合建立的[21, 22]. 高速入射的高电荷态重离子与固体靶相互作用的内壳层过程比轻离子入射过程要复杂得多，由于实验条件的限制，实验数据比较匮乏，该能区实验值和理论计值对比的分析鲜有报道，哪种理论模型适合，需要进一步的实验验证.

本实验用电子冷却存储环提供的能量为165 MeV/u C6+的高能离子脉冲束分别轰击Ti、V、Fe、Ni和Zn靶，探测到了各固体靶的K壳层X射线发射谱. 测量了炮弹离子在同一入射条件下激发各靶的KX射线的位置. 分别计算了X射线的产生截面，并将BEA，PWBA和ECPSSR理论计算值与实验值进行比较.

2 实验方法

中国科学院近代物理研究所的电子冷却贮存环(Cooling Storage Rings，CSR)可以提供能量高达900 MeV/u(C6+)的束流，流强达到105-108个/周期. 我们利用CSR提供动能为165 MeV/u的高电荷态C6+脉冲束流入射原子序数不同的固体靶表面，束斑面积可通过CsI晶体测量，大小为5*5 mm2，束流强度约为108个/脉冲. 考虑到离子束到达靶之前穿透空气介质的能量损失，打靶时离子实际能量为154.26 MeV/u. 离子束垂直入射(45度观测)表面洁净的Ti(纯度98%)、V(纯度99.99%)、Fe(纯度96%)、Ni(纯度99.99%)和Zn(纯度99.99%)靶固体表面，靶厚度分别为4.02 mm、0.30 mm、0.10 mm、0.05 mm和0.02 mm. 靶X射线的探测通过Si漂移XR-100SDD型探测器进行，探测面积为7 mm2，探测口前铍窗的厚度为12.5 μm；峰化时间9.6 μs，增益100的情况下，可探测的能量范围是0.5 keV～14.55 keV；能量分辨率为136 eV. 实验时，探测器距离靶点100 mm，与入射束流方向成135°角，探测口的几何立体角为7×10-4sr. 入射离子的个数通过法拉第圆筒和束流终端的计数器间接给出. 实验前用标准放射源55Fe 和241Am对探测器进行了刻度.

3 结果与讨论

3.1 高能C6+脉冲束引起靶原子X射线谱

图1为动能154.26 MeV/u C6+脉冲离子束分别入射Ti、V、Fe、Ni和Zn靶表面激发的靶原子K壳层特征X谱线. 由图可见实验测的原子序数不同的各靶KX谱线结构基本一致，所有谱线均为双峰结构. 这两个峰的形成是由于靶原子的K壳层电子被炮弹离子激发，形成空穴，L和M支壳层的电子分别向K壳层跃迁辐射产生的Kα和Kβ射线. 由于本实验探测器分辨率和测量时间的限制，未能分辨出Kα和Kβ射线所包含的四个峰，分别主要为Kα1(2p3/2-1s)、Kα2(2p1/2-1s)、Kβ1(3p3/2-1s)、Kβ3(3p1/2-1s)，Kα和Kβ特征谱线电子跃迁示意图如图2所示. 实验中靶原子的L、M等壳层的X射线均未探测到，是由于空气介质的自吸收以及探测器的效率主要在低能量段所致.

将图1分析出的各靶K-X射线峰中心位置与美国劳伦斯伯克利国家实验室(Lawrence Berkeley National Laboratory，LBNL)X射线与现代光源中心(Center for X-ray Oprics and Advanced Light Source)提供的数据对比，列于表1. 由表可见各固体靶的K-X射线的实验测量值跟文献值相比均向高能区发生了不同程度的移动. 例如，固体靶Ti的Kα射线向高能区能移60 eV，Kβ射线向高能区移动48 eV；靶Zn的Kα射线向高能区能移81 eV，Kβ射线向高能区移动88 eV，其它各靶的情况各有不同，详见表1. 对表中的数据分析发现，在相同入射条件下靶原子X射线向高能区能移量与靶原子序数关联不大，没有明显规律. 分析能移的原因，我们考虑到高速重离子入射固体靶表面时，会与靶原子内的多个电子同时作用，引起靶原子内壳层发生多电离，同时伴随着核外各壳层多个空位的产生. 原子核外出现多个空位时，核电荷屏蔽减小，从而内壳层中剩余电子的束缚能被扰动，导致了测量到的X射线向高能区移动.

图1 动能为154 MeV/u的C6+脉冲离子束入射(a)Ti、(b)V、(c)Fe、(d)Ni和(e)Zn靶表面激发的靶原子K壳层特征X谱线Fig. 1 Characteristic of K-shell X-ray spectra induced by 154 Mev/u C6+impacting on (a)Fe, (b)Co, (c)Ni, (d)Cu and (e)Zn targets

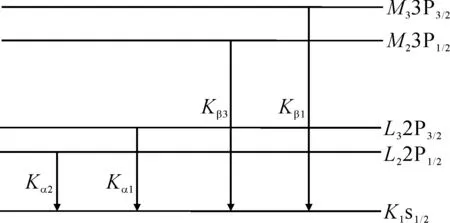
图2 Kα和Kb特征谱线电子跃迁示意图Fig. 2 Electron transition diagram of the lines of Kα and Kβ X-rays

表1 靶原子X射线能量测量值与文献值[23]的比较

而L壳层多重电离效应可以通过分析K壳层X射线的能量偏移或者利用高分辨率晶体光谱仪探测到的K-L转变过程中X射线相对强度分布来确定. 根据实验结果，利用多组态Dirac-Fock方程，可以根据能量的偏移量估算，由于高电荷态重离子的作用靶原子上大概产生了2～3个2p空穴. 多电离的另一个影响是改变荧光产额，2p电子多电离将导致Kα荧光产额降低，而Kβ荧光产额增加. 表2给出了 154 MeV/u C6+离子和低能H+离子轰击Ti、V、Fe、Ni和Zn各靶时靶原子K壳层X射线峰强度比. 如表2所示，高能C6+入射Ti靶时Kβ与KαX射线的强度比约为质子入射Ti靶的2.5倍，而对于其它的各靶也存在大约1.4～1.9倍的比例. X射线强度比的变化又一次证明了高电荷重离子引发靶原子的多电离效应.

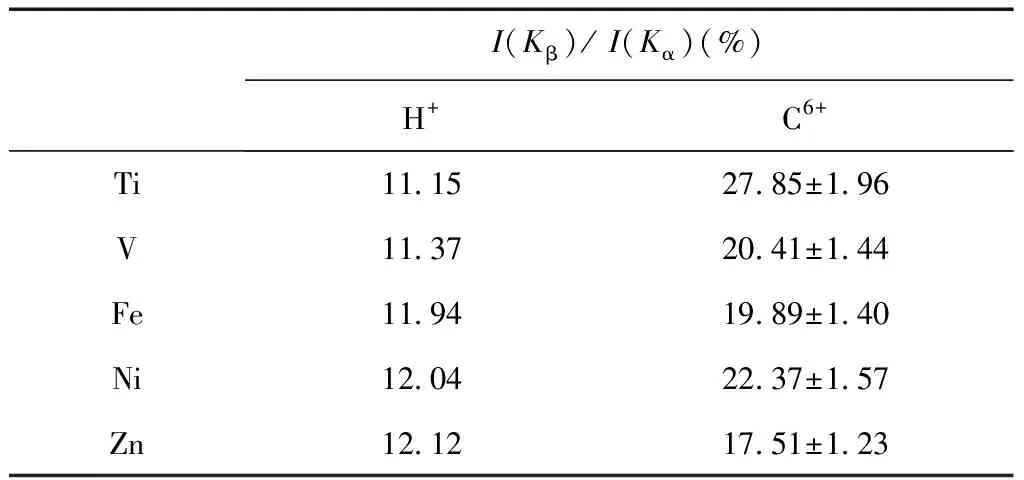
表2 154 MeV/u C6+离子和低能H+离子轰击[2]Ti、V、Fe、Ni和Zn各靶时靶原子K壳层X射线峰强度比

3.2 靶原子K壳层X射线产生截面的计算

当高能1848 MeV C6+脉冲束轰击固体薄靶时，其X射线产生截面可以通过测量X射线计数来计算，按公式σX=Nx/nNPεdft(Ω/4π)进行，式中n为单位面积内的靶原子数. 本实验中C离子在固体靶Ti、V、Fe、Ni和Zn中射程分别为19.8 mm、17.0 mm、18.0 mm、18.8 mm、28.4 mm，远大于各固体靶中K-X射线的衰减长度，X射线计数统计时需要考虑靶的吸收，故以上计算薄靶X射线产生截面的公式将不能直接应用. 本实验中，入射粒子在固体靶中X射线衰减长度内能量损失比较小，不到0.024 MeV/u，可近似认为入射粒子的能量不变. 考虑到实验中测量的靶原子X射线在靶中的自吸收和空气介质的吸收，高能离子入射薄靶的X射线产生截面的实验值计算公式可修正为[18].

(1)

其中μ为射线在靶中的衰减常数，Nx为X射线光子数，Np为入射粒子数，ρ为单位体积内的靶原子数，εd为探测器效率，ft为靶和探测器之间介质的吸收系数，Ω为探测器所张的立体角，L为靶的厚度. 实验结果的不确定度主要来源于X射线的计数统计(<5%)，入射离子的计数统计(<10%)，立体角误差(<6%)，考虑误差传递产生截面的最大不确定度为13%.

运用(1)式分别计算了能量154 MeV/u的C6+入射Ti、V、Fe、Ni和Zn固体靶表面时，激发靶原子的K-X射线的实验产生截面，其计算结果如图3所示. 由图可见，计算出的X射线产生截面数值在103bar量级，而且入射条件相同的情况下，靶原子K-X射线的产生截面随原子序数的增加有减小的趋势，Ti靶和Fe靶的实验值有点偏离，可能是由于靶纯度不高造成的.

按照原子结构和光谱理论，对于靶原子K壳层X射线的产生截面理论上可以通过(2)式计算得到：

(2)

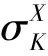
(3)

G(V)=[V2/(1+V2)]3/2V-2×[V2/(1+V2)+

[1-1/α][1-(1/α)1+V2]

(4)

其中N是对应i壳层的电子个数，Z是入射离子的电荷态，σ0=πe4=6.56×10-14cm2eV2，U为电子束缚能，G(V) 是约化速度的函数，约化速度V=vp/vi(vp是入射离子的速度，vi是i壳层电子的平均速度)，α=4V2(1+1/V)，对于V<0.206时[19]，可近似的取G(V)=4V4/15.

基于PWBA和ECPSSR理论模型，我们利用ADDS-V4-0版本的ISICS程序分别计算了154 MeV/u的C6+脉冲束轰击Ti、V、Fe、Ni和Zn固体靶表面时Kα和KβX射线产生截面，计算结果同实验产生截面和BEA模型计算结果一并见图3.

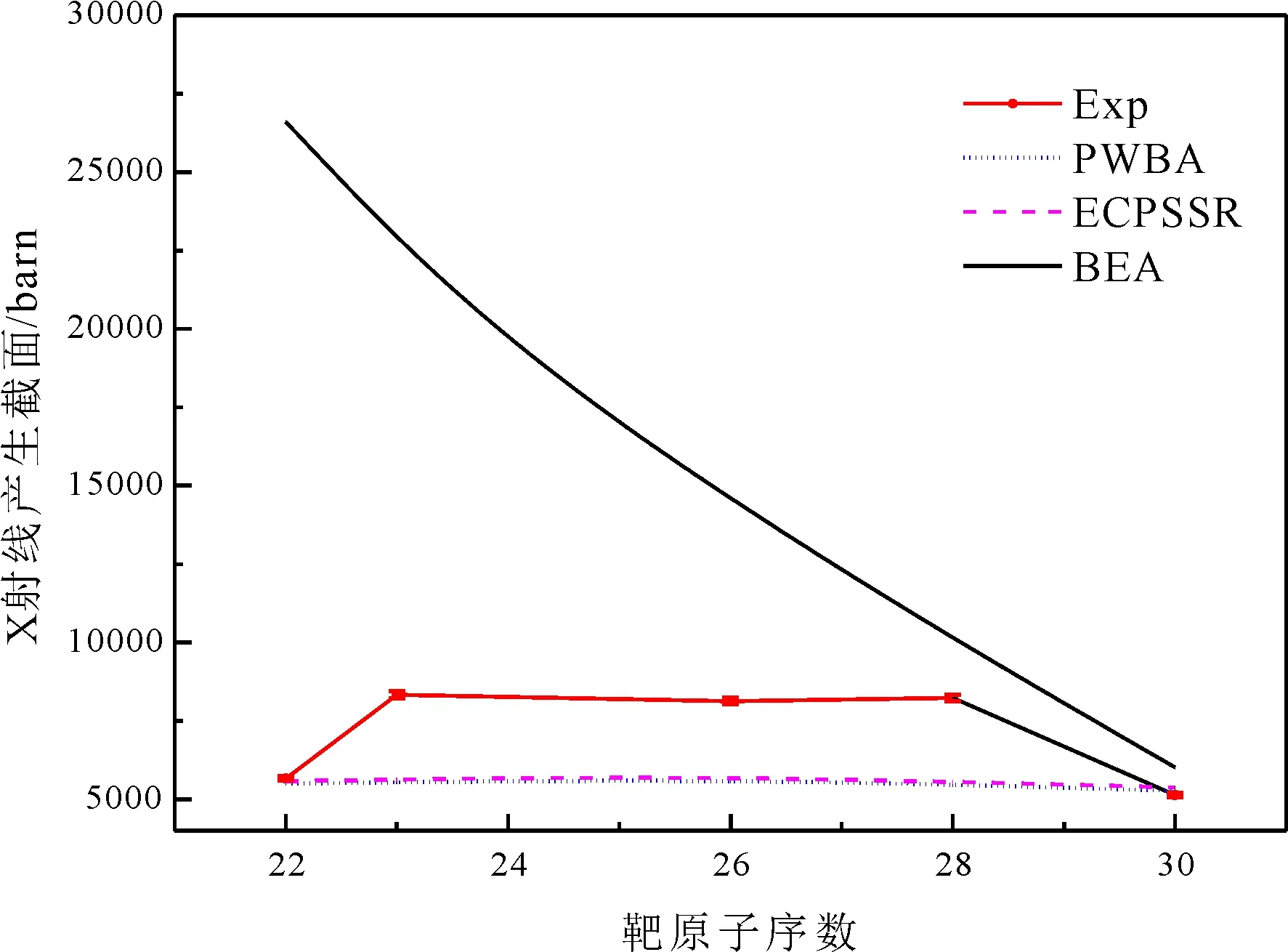
图3 154 MeV/u C6+诱发各靶的K-X射线产生截面Vs靶原子序数Fig. 3 Comparisons of the experimental K-shell x-ray production cross sections of Ti, V, Fe, Ni and Zn for 154 MeV/u C6+ion impact with their theoretical calculations from BEA, PWBA, and ECPSSR models

由图3可见利用平面波玻恩近似模型(PWBA)和ECPSSR理论模型计算各靶的K-X射线总产生截面接近，两者比实验结果明显偏小. ECPSSR理论是在PWBA基础上的修正，因此两种理论的计算结果近似. 与以上两个理论相比较，应用BEA模型计算的理论值比实验值明显偏大，对于Ti、V、Fe和Ni靶，实验测到的K-X射线产生截面比利用BEA模型计算的理论值小一个数量级，而对Zn靶则实验值跟BEA理论值接近. 整体上利用BEA模型计算的靶原子K-X射线的产生截面随原子序数的增加而减小.K-X射线产生截面的实验值除Ti以外，也符合靶原子K-X射线的产生截面随原子序数的增加而减小的规律. 接下来将会对BEA模型进行适当修正，比如考虑入射离子有效电荷态修正以及库仑偏转修正等. 对于Ti的K-X射线的产生截面数据与其他规律不符，后期的实验将会进一步验证.

4 结 论

实验分别测量了154 MeV/u的C6+脉冲离子束入射原子序数从22(Ti)到30(Zn)固体表面时激发靶原子的Kα和Kβ特征X射线. 实验发现高能重离子脉冲束轰击固体靶时发生了多电离效应，从而导致靶原子的Kα和Kβ特征X谱线的能量向高能区发生了不同程度的偏移，偏移量跟原子序数的大小无明显关联. 计算了入射条件确定(154 MeV/u，C6+)的前提下，各靶的K-X射线的产生截面. 发现该产生截面的实验值随原子序数的增大而减小，该变化趋势与BEA模型计算的理论值接近，但BEA模型计算的理论值偏大，欲利用BEA模型分析该能区靶原子的X射线产生截面还应对模型做相应的理论修正. 而PWBA模型和ECPSSR模型的计算结果虽在数量级上与实验结果相同，但其变化趋势不符. 欲用该模型更好的描述本实验结果需要对理论做进一步修正，我们今后将在此方面做出更多的努力.

致 谢：作者对中国科学院近代物理研究所CSR上全体工作人员的辛勤工作表示衷心感谢.