一种单天线ADS-B交织信号分离算法*

(四川大学 电子信息学院，成都 610065)

0 引 言

广播式自动相关监视(Automatic Dependent Surveillance-Broadcast，ADS-B)是一种安装在飞机上的新型监视系统，它利用卫星导航技术并采用全向广播的方式定期向空中交通管制中心和附近的其他飞机发送其飞行器编号、空中位置、运行速度等信息[1]。这种新型监视技术的应用能有效提升管制员和飞行员对飞机态势的感知能力，扩大监视覆盖范围，提高空中交通安全水平、空域容量与运行效率。与传统的雷达监视技术相比，ADS-B具有成本低、精度误差小、监视能力强等优点，因此，它在未来民航监视系统中发挥着越来越重要的作用，已成为国际民航组织(International Civil Aviation Organization，ICAO)未来空中导航系统项目的重要组成部分[2]。

近年来，随着民航业的不断发展，飞机数量也在日益增加，这使得接收到的ADS-B信号可能存在多条报文交织的情况。在ICAO制定的文件标准中，对交织报文的处理方法如下：当前导中出现交织时，对信号强度最大的报文进行解码，并放弃其他报文；当数据块中出现交织时，对先到的报文进行解码，并放弃其他报文[3]。若按此标准进行信号处理，则任何情况下都只有一条报文能够正确解码，这将会大大降低系统的监视容量。因此，如何有效分离出ADS-B交织信号中的各条报文，成为当前急需解决的一个问题。

目前，较为主流的交织信号处理方法是，利用阵列天线接收信号，再采用阵列信号处理的方法从空域上将其进行分离。例如，文献[4]使用均匀线性阵列天线接收二次雷达(Secondary Surveillance radar，SSR)信号，并估算出交织信号个数及其波达方向(Direction of Arrival，DOA)，再利用最大似然估计分离交织信号。文献[5]采用阵列天线接收SSR信号后，利用信号源的时间稀疏性，提出了一种基于投影技术的交织信号分离算法。文献[6]则根据S模式信号的编码特性，采用曼彻斯特解码算法对交织信号进行分离。此外，针对阵列信号，还有快速独立主成分分析(Fast Independent Component Analysis，Fast ICA)[7]、MUSIC[8]、自适应波束成形[9]等分离算法。

但与阵列天线接收机相比，单天线ADS-B接收机的使用更加普遍，且具有成本低、易维护等优点。因此，如何分离单天线ADS-B交织信号受到了众多研究者的关注。文献[10]提出了一种基于累加分类的ADS-B二重交织信号分离方法，在得到两个信号的相对时延后对信号数据进行累加并利用K-means方法进行分类，最终得到比特位判决以实现交织信号分离，但该方法需要保证两个信号存在着一定的功率差。文献[11]提出利用单通道ICA算法进行信号分离，但该方法要求混合信号相互独立且频谱不相交，故不适用于ADS-B交织信号。文献[12]通过重构应答信号矩阵，将单天线问题转化为多天线问题，利用投影算法(Project Algorithm，PA)来分离信号，但该方法对信号的时延和信噪比要求较高。

针对现有方法存在的不足，本文提出了一种PA算法与卷积神经网络(Convolutional Neural Network，CNN)相结合的分离方法，降低了对交织信号信噪比以及功率差的要求。

1 ADS-B信号模型

一帧完整的ADS-B应答信号如图1所示，前8 μs为信号的前导，由位置分别固定在0.0 μs、1.0 μs、3.5 μs以及4.5 μs的四个脉冲组成，每个脉冲的持续时间为0.5±0.05 μs；后112 μs为信号的数据块，采用脉冲位置调制(Pulse Position Modulation，PPM)编码，共包含了112 b的数据[3]。每比特数据所占时间为1 μs，包含了两个chip，当脉冲出现在前一个chip时代表数据“1”，出现在后一个chip时代表数据“0”，其中脉冲的持续时间为0.5±0.05 μs。

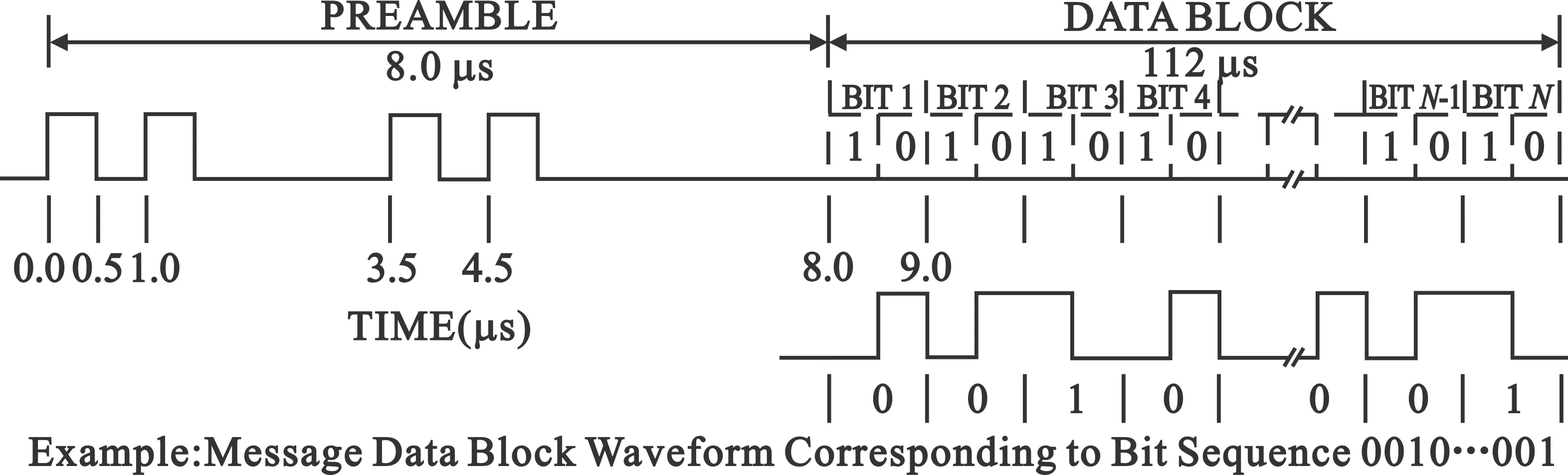
图1 ADS-B应答信号结构图

由此，基带ADS-B信号可表示为

(1)

式中：c[k]表示每一个chip的值，为“0”或“1”；p(t)表示脉宽为T=0.5 μs的矩形脉冲。为便于信号在信道中的传播，将其调制到1 090 MHz，允许存在±1 MHz的偏差。由于偏差的存在，接收机将调频信号下变频到基带后仍会有频差。

采样后，接收到的单天线ADS-B二重交织信号如图2所示，可表示为

x=s1+s2+n。

(2)

图2 ADS-B二重交织信号

源信号s1、s2的每一个采样点s1m、s2m又可以表示为

(3)

(4)

式中：P1、f1和C1[m]分别表示前一个信号的功率、频率偏差以及采样点取值，P2、f2和C2[m]则分别表示后一个信号的功率、频率偏差和采样点取值，Ts表示采样周期。

2 单天线PA算法

2.1 虚拟阵列信号的构建

当采样率为10 MHz即1 μs包含10个采样点时，每次选取连续的d=5个点[12]，将信号矢量x=[x1x2…xM]重构为d行l=M/d列的虚拟阵列矩阵。d的值相当于模拟天线的个数，而在此处选择d=5的原因是应答信号中一个chip刚好包含5个采样点，如果选择其他值则每列包含的数据没有规律性，不利于信号的分离。可将重构后的虚拟阵列信号矩阵表示为

(5)

则式(2)可重新表示为

X=S1+S2+N。

(6)

式中：S1、S2和N的维数与X相同，都为d×l的矩阵。

重构后的源信号S1、S2可看作

S1=A1V1，

(7)

S2=A2V2。

(8)

式中：A1、A2为两信号的虚拟导向矢量，维数为d×r1和d×r2，r1、r2为矩阵S1、S2的秩，通常情况下为1；V1、V2维数为r1×l和r2×l。

将式(7)、式(8)代入式(6)可得

X=A1V1+A2V2+N=

AV+N。

(9)

式中：导向矩阵A的维数为d×(r1+r2)，矩阵V的维数为(r1+r2)×l。

2.2 交织位置检测

先利用一个固定大小的滑动窗口对虚拟阵列信号X进行分隔，每次得到一个包含4 μs即40个采样点的子矩阵Xsub，其矩阵维数为d×8；再对每个子矩阵Xsub进行奇异值分解，可表示为

Xsub=PΣQT。

(10)

式中：P=[p1,p2,…,pd]为左奇异值矩阵，其矩阵维数为d×d，且p1到pd为子矩阵Xsub的特征向量；Q为右奇异值矩阵，其矩阵维数为8×8，且P和Q均为单位正交矩阵，符号“T”表示对矩阵求转置；Σ是维数为d×8的对角矩阵，可将其表示为

(11)

式中：σ1～σd为子矩阵Xsub的特征值，并按数值从大到小降序排列。

根据以上方法，可以求出每个滑动窗口中子矩阵Xsub的特征值，组合而成的虚拟阵列信号X的特征值变化曲线如图3所示。因第五个特征值σ5的数值很小未在曲线图中画出。

图3 特征值变化曲线

根据特征值大小的变化可以确定四个转折时间点t1、t2、t3以及t4，其中t1～t2时刻只包含前一个信号X(1)，t3～t4时刻只包含后一个信号X(2)。为了能区分出t1和t2时刻，要求后一个信号相对前一个信号的时延要大于0.5 μs。由此，可将两个时间段的信号分别表示为

X(1)=AV(1)+N(1)，

(12)

X(2)=AV(2)+N(2)。

(13)

又因为V(1)仅包含前一个信号V1的一部分，V2此时为零矩阵；V(2)仅包含后一个信号V2的一部分，V1此时为零矩阵，故可将式(12)、式(13)分别写作

X(1)=A1V1(1)+N(1)，

(14)

X(2)=A2V2(2)+N(2)。

(15)

2.3 导向矢量估计与信号分离

对X(1)、X(2)进行奇异值分解，选取前r1、r2个特征值所对应的特征向量作为虚拟导向矢量A1、A2，进而得到导向矩阵A=[A1|A2]。

根据导向矩阵A，可得到能恢复重构源信号的加权矩阵W，即

W=A†=[AHA]-1AH

。

(16)

式中：符号“†”表示矩阵的伪逆 。

对源信号S1、S2来说，其加权矩阵分别为

W1=[A10d×r2]W，

(17)

W2=[0d×r1A2]W。

(18)

由加权矩阵W1与接收到的交织信号X，可得到分离后的源信号S1的估计值如下：

W1AV+W1N=

[A10d×r2]WA†V+W1N=

[A10d×r2]AAV+W1N=

A1V1+W1N=

S1+W1N。

(19)

同理，可得到分离后的源信号S2的估计值

(20)

对于图2所示的ADS-B交织信号，经过以上算法分离后的前后两信号分别如图4和图5所示。

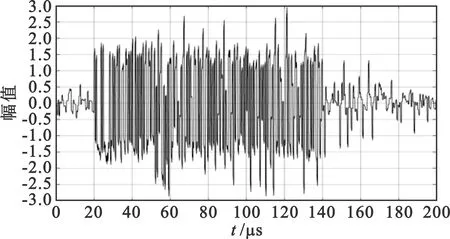
图4 分离后的前一个信号

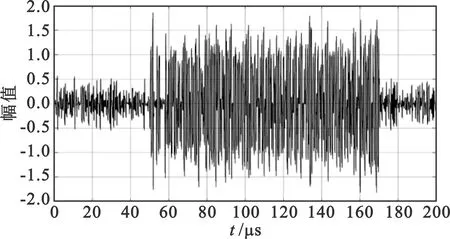
图5 分离后的后一个信号

从图4和图5中可以看出，分离出来的信号脉冲中含有大量毛刺，这对后续解码过程中的比特判决以及置信度判定影响较大，可能导致解码失败。因此，需要对分离出来的信号进行波形修正，以提高解码成功率。

3 CNN 编解码器的修正

3.1 CNN编解码器的结构

卷积神经网络主要用于图像处理领域，如图像分类[13]、图像样式转换[14]以及人脸识别[15]等，较少应用在通信信号的处理中。但由于灰度图片的本质是一个矩阵，而时域传输信号也能看作一个矢量或矩阵，故将CNN应用于对ADS-B信号的处理是可行的。

针对采样率为10 MHz的信号，首先搭建一个如图6所示的CNN编解码器模型。该模型可以分为编码器以及解码器两大部分，其中，编码器包含一个输入层和5个隐藏层，解码器包含5个隐藏层和一个输出层。经过编码器的特征提取，将输入信号压缩成更短的只包含重要特征的序列，再经过解码器的合理插值，使之扩增为与输入信号长度一致的序列后输出。要使输出的重建信号成为期望的波形凭证的信号，就要先对编解码器进行训练，使其中的可变参数都接近最佳值。

图6 CNN编解码器结构图

3.2 样本选择

训练编解码器需要大量输入样本及其对应标签，即需要大量的带噪ADS-B应答信号及其对应的纯净信号。但不存在完全不含噪声的ADS-B应答信号，且一个完整信号包含的采样点数较多，直接作为输入会使得模型中参数过多，增加训练的复杂度。因此，采用大量如图7所示的含有噪声的随机方波脉冲作为输入信号，其信噪比为0 dB。相应地，图8所示的对应纯净信号作为标签，即期望信号。

图7 输入信号

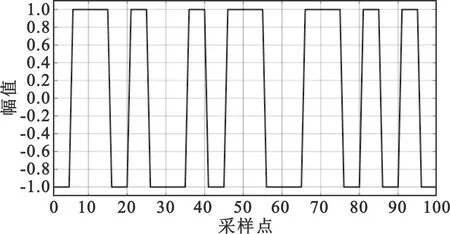
图8 标签信号

3.3 模型训练

可以将CNN编解码器的训练分为两个过程，即前向传播过程以及反向传播过程。其中，前向传播过程用于计算每一层的输出并将其保存下来，反向传播过程则用于更新每一层的权值参数。

对于前向传播过程，每一个隐藏层的输出可以表示为

al=σ(zl)=σ(al-1*Wl+bl)，l=2,3,…,L。

(21)

式中：al-1表示上一层的输出即当前层的输入，Wl表示上一层与当前层之间的卷积核的参数，bl表示当前层的偏置值，zl表示当前层的线性卷积输出，al表示当前层经过激活函数处理后的输出，L表示输出层，符号“*”表示卷积处理。值得注意的是，为了便于后续反向传播过程的运算，需要将每一层的输出al(l=2,3,…,L)保存下来。

将最后的输出序列aL与给定的标签即期望序列y进行比较，可以得到样本误差。为了定量地分析样本误差的大小，将损失函数也即误差函数定义为

(22)

为了使总的损失函数值J(W,b)达到最小，需要不断地更新参数W和b以找到其最佳值，即训练CNN编解码器时的反向传播过程。若要加快损失函数J(W,b)的收敛速度，即用更少的迭代次数找到其最小值，就要保证参数是沿着损失函数J(W,b)梯度的反方向即函数值减小最快的方向更新的。

各卷积层中参数W和b的更新递推式为

(23)

(24)

式中：k表示当前的迭代次数；m表示单次送入CNN 编解码器进行训练的样本个数；α表示学习速率；l=2,3,…,L;δl为各卷积层的灵敏度，定义为

(25)

至此整个训练过程结束，即完成了CNN 编解码器的前向传播过程以及反向传播过程。

3.4 幅值修正

训练完成后，将图4和图5所示的分离后的信号都分割成与输入样本采样点相同的信号片段，依次送入编解码器进行幅值修正。修正完成后，再将输出的信号片段顺次拼接成完整信号，其波形如图9和图10所示。对修正后的信号进行解码，可得到通过循环冗余校验(Cyclic Redundancy Check，CRC)的112 b的十六进制分别为“8D 78 16 10 99 14 5F 9D 10 04 09 36 B1 8A”和“8D 78 10 1A 20 30 B1 79 DB 7E 60 E6 B6 30”。

图9 CNN修正后的前一个信号

图10 CNN修正后的后一个信号

综合第2、3节所述内容，可得到改进单天线PA分离算法的步骤如下：

Step1 将单天线ADS-B二重交织信号x重构为虚拟阵列信号X。

Step2 利用滑动窗口选取信号子矩阵Xsub进行奇异值分解，以确定两个源信号的起始时刻t1、t2以及终止时刻t3、t4。

Step3 根据四个时刻选出仅包含一个信号的部分X(1)、X(2)，对其进行奇异值分解得到虚拟导向矢量A1、A2，组合成导向矩阵A。

Step4 根据导向矩阵A的伪逆得到两个源信号的加权矩阵W1、W2。

Step6 将得到的估计值还原成单天线信号后，再利用CNN模型对其进行幅值修正。

4 实验与分析

图2所示的仿真ADS-B二重交织信号中，前后两交叠信号的频率差为0，信噪比(Signal-to-Noise Ratio，SNR)为12 dB，且后一个弱信号相比于前一个强信号衰减了3 dB。对该样例，经过PA算法以及CNN编解码器的处理后，可以正确解码并提取出报文所包含的信息。

因接收机不能做到理想的相干解调，所以将接收信号下变频到基带后，前后两交叠源信号会存在一定的频率差。频率差值的不同对分离后信号解码率的影响也不同。生成了几种不同频率差下信噪比为12 dB、强度差为3 dB的仿真单天线ADS-B二重交织信号各10 000个。观察分离后弱信号的解码成功率变化，找到频率差对其的影响规律，具体的解码成功率见表1。

表1 不同频率差下弱信号的解码成功率

由表1可看出，频率差越大越容易将交织信号分离出。考虑到实际信号中前后两交叠信号的频率差不会太大，故后续的仿真实验样本频率差都取为0.01 MHz。

为了进一步验证该改进PA算法的可行性，随机生成了信噪比从7～16 dB、强度差为3 dB的仿真ADS-B二重交织信号各10 000个进行测试。比较不同信噪比下CNN编解码器处理前后分离弱信号解码成功率的变化，以此来评价改进算法的性能。测试结果如表2所示。

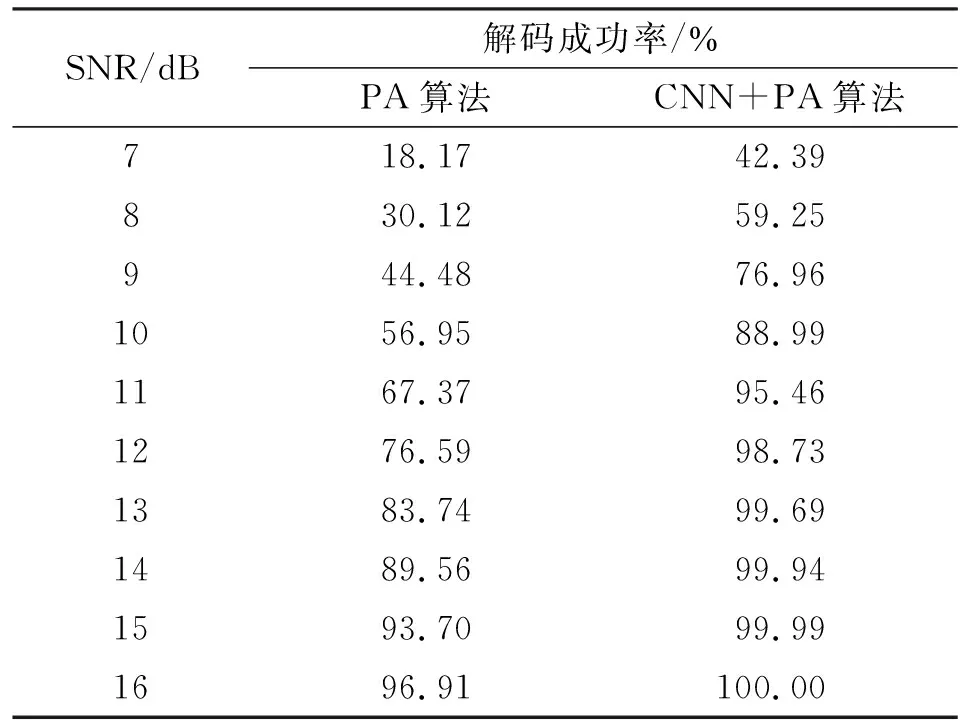
表2 不同信噪比下弱信号解码成功率对比

除此之外，还选择了信噪比为12 dB、强度差从0～6 dB的仿真ADS-B二重交织信号各10 000个进行测试，观察不同强度差下CNN编解码器处理前后分离弱信号解码成功率的变化来验证改进算法的性能。具体的解码成功率见表3。

表3 不同衰减强度下弱信号的解码成功率

从表2和表3中的解码率的变化能看出，经过CNN编解码器处理后分离弱信号的解码成功率都得到了显著的提升。因此，结合CNN编解码器后的PA分离算法对不同信噪比、强度差的ADS-B二重交织信号都具有可行性。

5 结 论

ADS-B监视系统性能的好坏取决于接收端信号的解码成功率。为了实现单天线ADS-B二重交织信号的分离，以提高其解码成功率，提出了一种PA算法与CNN编解码器相结合的分离方法：首先将单天线ADS-B二重交织信号重构为虚拟阵列信号，接着利用PA算法对其进行分离，最后将分离信号通过训练好的CNN编解码器进行幅值修正。为了评价该方法的性能，将分离出的弱信号进行解码，并以通过CRC校验为解码成功的标准。实验结果表明，经过该方法处理后的分离信号，其解码成功率得到了显著的提升，即该方法具有可行性。