High-Precision Vital Signs Detection Method Based on Spectrum Refinement and Extended DCMA

Mingxu Xiang,Wu Ren,Weiming Li,Zhenghui Xue

Abstract:In this paper,the spectral estimation algorithm is extended to the detection of human vital signs by mm-wave frequency modulated continuous wave (FMCW) radar,and a comprehensive algorithm based on spectrum refinement and the extended differentiate and cross multiply algorithm (DCMA) has been proposed.Firstly,the improved DFT algorithm is used to accurately obtain the distance window of human body.Secondly,phase ambiguity in phase extraction is avoided based on extended DCMA algorithm.Then,the spectrum range of refinement is determined according to the peak position of the spectrum,and the respiratory and heartbeat frequency information is obtained by using chirp z-transform (CZT) algorithm to perform local spectrum refinement.For verification,this paper has simulated the radar echo signal modulated by the simulated cardiopulmonary signal according to the proposed algorithm.By recovering the simulated cardiopulmonary signal,the high-precision respiratory and heartbeat frequency have been obtained.The results show that the proposed algorithm can effectively restore human breathing and heartbeat signals,and the relative error of frequency estimation is basically kept below 1.5%.

Keywords:vital signs detection;frequency modulated continuous wave (FMCW) radar;frequency spectrum refinement;high-precision frequency estimation

Human communication is mainly based on the good electrical conductivity of the human body,utilizing the body as the medium of information transmission to realize information interaction with equipment [1].In some cases,the transmission of vital characteristic parameters is required.Considering the limitation of application scenarios,the acquisition of these parameters increasingly dependson noncontact detection technology [2]. Among them,the frequency modulated continuous wave (FMCW) Doppler radar has been widely studied and applied in the monitoring of physical signs due to its advantages of small size,wide bandwidth,high resolution and low influence by the surrounding environment[3−5].How to obtain high precision cardiopulmonary frequency information in radar detection has become one of the research hotspots.

At present,the application of FMCW radar in high precision ranging research has gradually matured.A Doppler frequency-based range ambiguity elimination method is proposed to deal with the serious noise in [6].In [7],the ratio of the amplitude of the three spectral lines in the DFT amplitude spectrum was calculated to achieve frequency correction.[8] combined Quinn algorithm and Aboutanios iterative algorithm to obtain the correct interpolation direction at the spectrum near the quantized frequency point,thus overcoming the defect of poor accuracy when the frequency is near the spectral line or at the center of the spectral line.[9] proposed an improved zoom fast Fourier transform (ZFFT)algorithm,which obtained the approximate value through fitting method and used it as the basis of spectrum thinning interval,and then used ZFFT for spectrum thinning. In [10],the spectrum range of refinement was redefined:by comparing the amplitudes of the spectral lines adjacent to the left and right half of the spectral interval from the peak line of the fast Fourier transform(FFT) amplitude spectrum,the one with the larger amplitude was selected as the end of the refinement frequency band to avoid the misjudgment of the direction of frequency interpolation.In [11],an interpolation algorithm based on the phase difference method was proposed to overcome the phase entanglement problem,which had high noise resistance under the condition of strong local random noise.However,these highprecision spectral estimation algorithms are seldom used to extract vital signs.Therefore,the spectral estimation algorithm is considered to be applied to cardio-pulmonary frequencies detection by FMCW radar to improve the detection accuracy.

Because the energy of the heartbeat signal is much less than that of the respiration signal,and the multiple harmonics of respiration in echo signal will interfere with the heartbeat signal,it is difficult to achieve accurate monitoring [3].Since FMCW radar is not accurate enough in extracting respiratory and heartbeat frequencies,a comprehensive algorithm based on spectrum refinement and the extended DCMA algorithm is proposed in this paper.By precisely locating the range window of the target,avoiding phase ambiguity when extracting the phase information of radar echo signal,and refining the local spectrum when estimating heart and lung frequency,high precision extraction of respiratory and heartbeat frequency has been realized.The simulation results show that the algorithm can effectively recover the simulated respiration and heartbeat signals from the radar difference frequency signals,and the relative errors of the respiration and heartbeat frequencies obtained are basically less than 1.5%.

1 Vital Signs Model in FMCW Radar

Assuming that the transmitted wave of the FMCW radar is a sawtooth modulated signal,it can be expressed as [12]

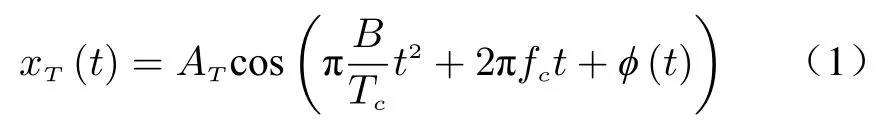
where xT(t) is the transmitted chirp signal,t is the propagation time of the signal,ATis the amplitude of the transmitted signal,fcis the initial frequency of the transmitted signal,B is the bandwidth of the chirp,Tcis chirp duration and φ(t) is the phase noise produced by the radar transmitter.

Breathing and heartbeat movements cause the chest to move,and radar signals are modulated by these movements as they reach the body.Assuming that the distance between the human target and the radar is R0,and there is a slight time-varying displacement r(t) caused by cardiopulmonary activities or other movements.Then the received signal reflected after the signal reaches the human body will produce a time delay td,and it is

where xR(t) is the received signal reflected after the signal reaches the human body,ARis the attenuation of radar signal;the time delay can be expressed by:td=2(R0+r(t))/c;c is the speed of light,the speed at which a signal travels through space.The radar receiver mixes the received signal with the transmitted signal,and the demodulated differential frequency signal is expressed in the I and Q channels as follows

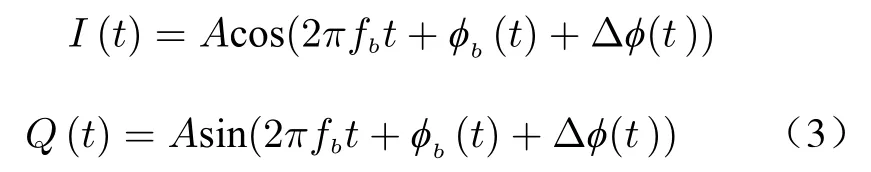
where I(t) and Q(t) are the demodulated differential frequency signal in the I and Q channels respectively,A is the amplitude of the difference frequency signal;fb=td·B/Tc≈2R0/c·B/Tcis the frequency of the differential frequency signal[13];Δφ(t)is phase noise;φb(t) is the phase generated by the movement of the human chest and the distance between the human body and radar,and it can be expressed by φb(t)=2πfctd+πB/Tc·td2,where the second term can be omitted because of B/Tc·td≪fc[14].Then φb(t) is

where λmaxis the wavelength corresponding to the frequency fc.Since the motion modes of chest fluctuation caused by respiration and heartbeat are similar to periodic vibration,they can be represented separately according to the periodic vibration of different amplitude and frequency caused by them,and the sinusoidal signal model meets this requirement. Considering that the chest fluctuation caused by respiration is about 1–12 mm and the frequency is 0.1–0.5 Hz,and the chest fluctuation caused by heartbeat is about 0.1–0.5 mm and the frequency is 0.8–2 Hz[15],the simulated respiration and heartbeat signal r(t) can be expressed as

where xr(t) and xh(t) are simulated respiration and heartbeat signals; Arand Ahare the amplitudes of respiration and heartbeat respectively which are the amplitudes causing chest fluctuation; frand fhare the frequency of respiration and heartbeat respectively,representing the information of cardiopulmonary signs of the human body; φrand φhare the initial phases of respiration and heartbeat.Based on (3),the differential frequency signal is represented as a complex signal as follows

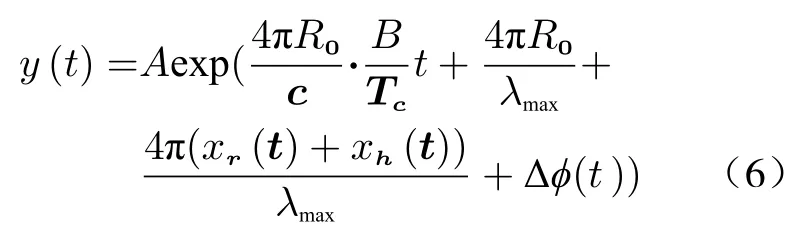
It follows that the frequency information of the physical sign signal is contained in the phase of the complex signal,and the magnitude of the item 4π(xr(t)+xh(t))/λmaxis vertically proportional to the wavelength.The higher the radar operating frequency,that is,the shorter the wavelength,the greater the phase modulation generated by the chest wall movement.For example,if the 77 GHz FMCW radar is selected,when the chest cavity produces 3 mm displacement due to cardiopulmonary movement,the corresponding phase modulation term is about 3π.At this time,the phase modulation term is much larger than π,so it is necessary to adopt appropriate methods to recover cardiopulmonary signals in the subsequent phase information extraction.

2 Principle of Hybrid Algorithm

A spectrum refinement method based on the extended DCMA algorithm is proposed for high precision estimation of respiratory and heartbeat frequencies.The algorithm is mainly divided into four parts: the first part is to extract the phase of the distance window where the target is,in which the improved discrete Fourier transform (DFT) algorithm is used to carry out the Fourier transform of the distance dimension,to obtain the accurate target range window,and to further extract the phase of the target in each frame period to obtain the initial phase information in the range window.The second part is the recovery of cardiopulmonary signals,that is,by the extended DCMA algorithm to process the phase obtained in the previous step,so as to restore the original cardiopulmonary signals as much as possible. In the third part,CZT algorithm is used to refine the local spectrum to achieve high-precision estimation of respiratory frequency.The fourth part is the heartbeat signal extraction and heart rate estimate.First the respiration and lower frequencies are filtered through a high-pass filter,and then design the notch filter group to filter 2– 4 respiratory harmonic components so as to reduce the effects of breathing harmonic component to the heartbeat signal,finally CZT algorithm is adopted to improve the frequency spectrum refinement for high accuracy of heart rate information.

2.1 Phase Extraction of Range Bin

2.1.1 High-Precision Range Bin Selection

The FFT of distance dimension is performed on the complex signal y(t) one chirp at a time,and the target distance corresponding to each chirp is obtained to form a range window. Then,the range window is used as the range unit where the target is located to extract phase information including chest motion. When FFT is used for range window extraction,due to the limitation of sampling rate and sampling points of this dimension,the frequency resolution is not high enough,leading to low accuracy.In this paper,the improved DFT algorithm is used to improve the accuracy of range detection.

Assuming that the sampling number of distance dimension is M and the sampling rate is fs,now analyze the situation of one chirp,and then the frequency resolution after FFT,Δf,is

According to the properties of the DFT [16],if the signal is multiplied by the factor exp(−j2π·u/v·m/M),an orthogonal basis can be obtained

where m is the sampling serial number of the differential frequency complex signal (m=0,1,2,...,M–1);v is the number of intervals between frequency bands to be refined,i.e.,the refinement multiple;u is the serial number of the spectral line in the current corresponding interval,and its value is [–v/2+1,v/2].When k takes the spectral line number M0corresponding to the peak value obtained by FFT of the original signal,the frequency range refined is [(M0−0.5)Δf,(M0+0.5)Δf].At this point,the frequency resolution becomes

2.1.2 Phase Extraction of Range Bin

The phase information is extracted by the arctangent method in the range window above.Due to the short radar wavelength,the actual phase will exceed the range of [–π,π] when the chest displacement is greater than a quarter of the maximum wavelength in the radar operating bandwidth. However,in computer calculation,only the phase in the first and the second quadrants can return [0,π],and the phase value in the third and the fourth quadrants can return[–π,0].Therefore,it is difficult to recover the original cardiopulmonary signal due to the phase ambiguity caused by breakpoints only through the arctangent method.There are two ways to solve this problem.

2.2 Respiratory and Heartbeat Signals Recovery

2.2.1 Phase Unwrapping

According to the characteristics of the arctangent algorithm,when a certain angle changes from 0 to 2π,the result obtained from the computer is 0 to π,–π to 0,and there is a jump at π,resulting in the output phases wrapped in [–π,π].Therefore,it needs to be corrected as follows [13].

Assuming that this moment phase value of φ(n),phase value of the next moment for φ(n+1),when the φ(n+1)−φ(n)>π,we need to add 2π to φ(n+1) for modifing; when φ(n+1)−φ(n)<−π,we need to modify φ (n+1) minus 2π.

2.2.2 Extended DCMA Algorithm

When the arctangent algorithm is used to extract the phase of a complex signal,the breakpoint phenomenon occurs,which leads to phase ambiguity.Thus,we need to consider the method to solve the breakpoint.In the DCMA algorithm,angular velocity is used to reflect the phase change [17],that is,the time derivative of the phase information obtained by the arctangent solution is carried out.We find that the angular velocity obtained at this time contains the information of chest displacement change,and there is no limit on the range of amplitude in the solution and thus it changes continuously,so the algorithm can be adopted to solve the phase breakpoint problem mentioned above.Then we integrate the diagonal velocity to inversely solve the phase information,and the expression is [18]

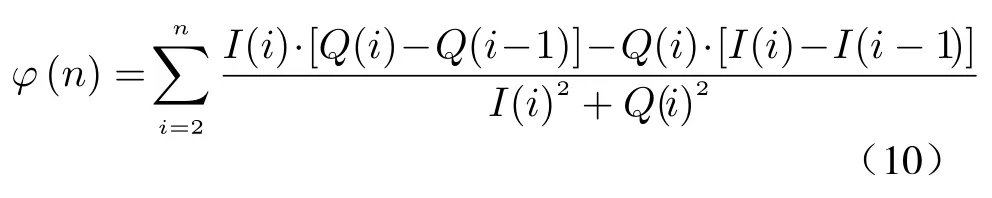
where φ(n) is the phase information obtained by the signals in the I and Q channels,which includes the physical sign information of the human body;I(i) and Q(i) are the sampling sequences of I(t) and Q(t) respectively,and I(i−1)and Q(i−1) are the sampling values of the previous moment relative to I(i) and Q(i) respectively.Since the denominator of φ(n) expression after re-integration does not equal 0,the phase obtained by this algorithm is continuously changing and there is no breakpoint problem,so the phase ambiguity problem is solved and the respiratory-and-heartbeat-signal can be recovered well.

The thermometer had dropped to 18 degrees below zero, but still chose to sleep in the porch as usual. In the evening, the most familiar sight to me would be stars in the sky. Though they were a mere1 sprinkle（） of twinkling dots, yet I had become so accustomed to them that their occasional absence would bring me loneliness and ennui2（） .

2.3 Respiratory Rate Estimation

The CZT algorithm is used to refine the spectrum for accurate estimation of respiratory frequency.Different from n-point FFT on the unit circle of the z-plane to calculate the frequency spectrum of equal interval sampling,the CZT algorithm calculates the frequency spectrum of equal interval sampling on the spiral line of the Z plane to realize the refinement of a certain spectrum.We transform the recovered phase φ(n) into φ(z).Assuming that an M-point is sampled in the Z plane with an initial phase of θ0and a sampling interval of φ0,calculate the value of φ(zk) at the fixed point zkas follows [19]

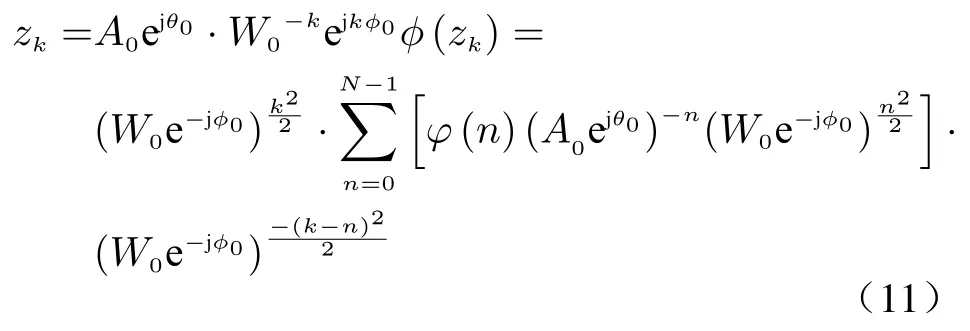
where A0is the vector radius length of the initial sampling point;θ0is the phase angle of the initial sampling point;φ0is the angle difference between adjacent sampling points;W0is the elongation of the helix. We set the spectrum range of CZT refinement as follows:the starting point is the position separated by half a spectral interval from the peak spectral line of FFT on the left,and the endpoint is the position separated by half a spectral interval from the peak spectral line on the right. Assuming that the spectral resolution of the restored cardiopulmonary signal after N-point FFT is Δf0=Fs/N and the peak spectral line obtained is N0,where Fsis the sampling rate of the restored cardiopulmonary signal,then the frequency band f1−f2to be refined is expressed as (N0−0.5)Δf0−(N0+0.5)Δf0.Then the parameters of CZT algorithm can be determined.Considering the spectrum analysis of the signal,the process is realized on the unit circle,that is,A0=1, W0=1, θ0=2π(N0−1)Δf0/Fs,φ0=2πΔf′0/Fs,where Δf′0is the required spectral resolution.If it can be realized after CZT sampling at point M,then

Then the sampling interval φ0can be expressed as

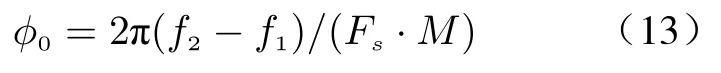
Finally,the selected A0,W0,θ0,φ0and the restored cardiopulmonary signals are substituted into (11) for calculation,and the frequency corresponding to the peak spectral line is the respiratory frequency.When the refinement multiple M is large,the algorithm flow shown in Fig.1 is generally used for calculation. And there is A=A0ejθ0,W=W0e−jφ0[19].

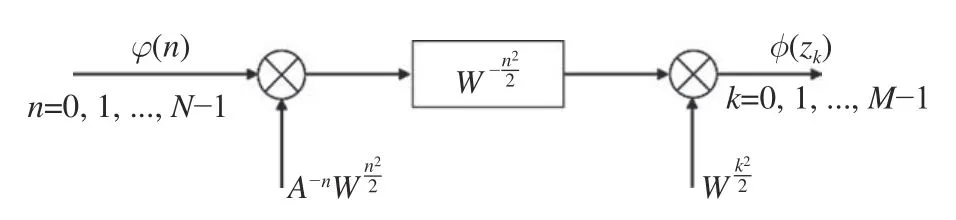
Fig.1 CZT calculation process

2.4 Extraction and Rate Estimation of Heartbeat Signal

Since the amplitude of chest vibration induced by human respiration is much larger than that of heartbeat,the respiratory signal is first filtered out during heart rate estimation. Considering that infinite impulse response (IIR) filter can be based on the results of mature analog filters in design,and can obtain higher selectivity with lower order than finite impulse response (FIR)filter,it occupies less computing resource.This paper adopts Butterworth IIR high-pass filter to filter the respiratory signal and lower frequency part.Set the breath frequency obtained in Section 2.3 as a point in the stopband of the highpass filter,and set the attenuation here as 25 dB.In order to retain enough heartbeat information and reduce the minimum passband frequency of the high-pass filter as much as possible,this paper chooses to set the point as adding 0.2 Hz on the basis of respiratory frequency.

Considering the influence of respiratory harmonics on the heartbeat signal,a set of notch filters are used to filter respiratory harmonics.Notch filter refers to the band-stop filter with a very narrow stopband,which can achieve the effect of rapid attenuation of the input signal at a certain frequency point.The transfer function of the notch filter,H(z),is analyzed in [20] as follows

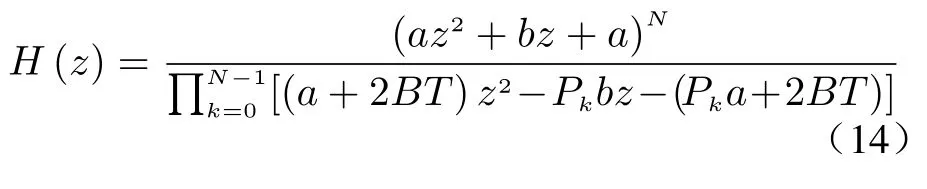
where N is the order of the filter;B is the stopband bandwidth of the filter;T is the sampling period;and a=4+, b=−8; Ω0is the stop-band center frequency of notch filter;Pk=exp[jπ(1/2+(2k+1)/2N)].

In order to reduce its computational complexity,N=2 is selected in this paper.Then the system function of the filter can be expressed as

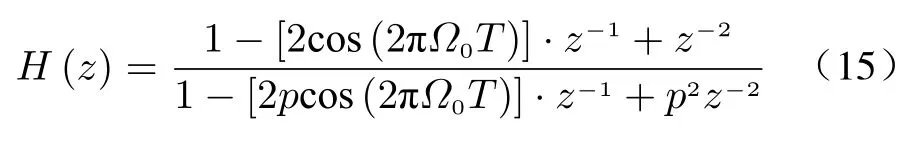
where p is a constant and p <1,and the closer to 1,the narrower the notch filter’s bandwidth is.

According to the normal range of cardio-pulmonary frequency,a set of notch filters is used to filter the 2－4 harmonic components of respiration,and the recovered heartbeat signal can be obtained.Finally,the heart rate can be estimated according to the algorithm in Section 2.3.And the proposed hybrid algorithm can be described as shown in Fig.2.

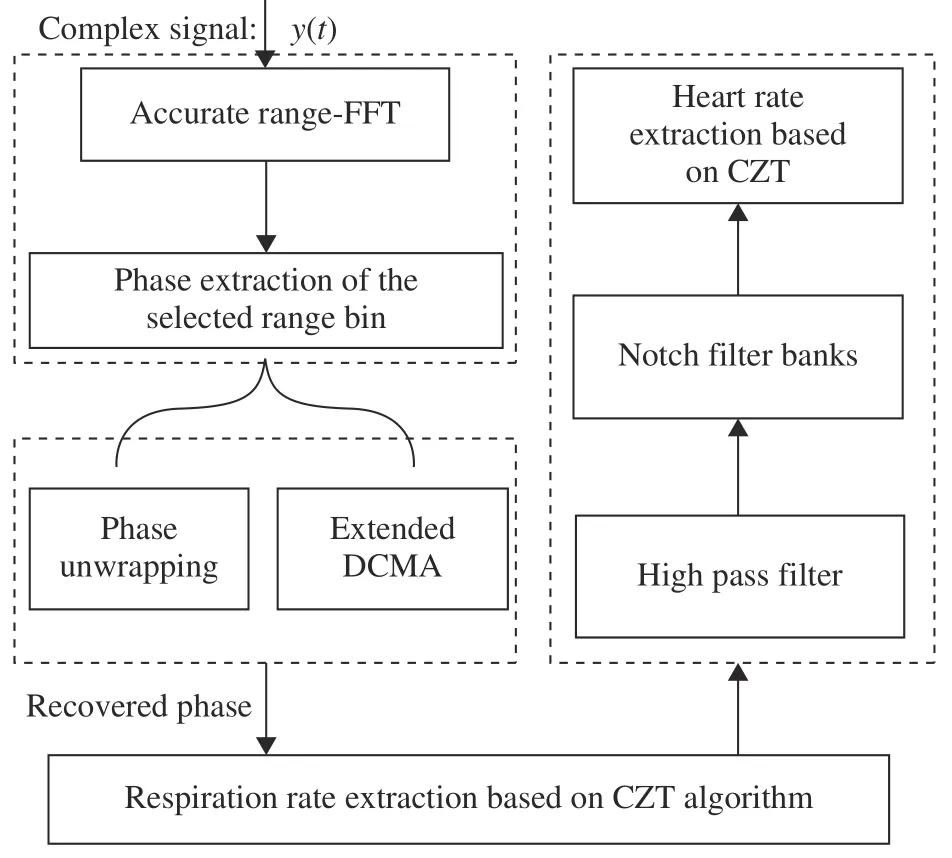
Fig.2 Proposed signal processing algorithm flow

3 Simulations and Results

3.1 Simulation Parameter Setting

The FMCW signal parameters constructed in the simulation are shown in Tab 1.Tab.2 shows the actual simulated position and physical sign information of the target human body.The subsequent simulation verification is based on this.The simulated FMCW signal is described as follows.

Tab.1 FMCW signal parameters

Tab.2 Simulation parameters

Assuming that the chirp repetition frequency of radar is 16 Hz,the chest movement of the human target is detected 16 times per second,which is also the slow time sampling rate fs.If the total number of pulses is 512,denoted by N,then (5) can be expressed as

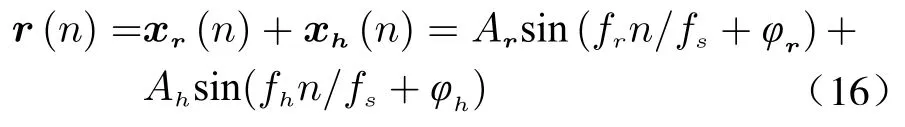
where n=0,1,2,...,N–1,and parameters Ar,Ah,frand fhare set according to Tab.2.If the analog-to-digital converter (ADC) sampling rate of FMCW radar is 3 MHz,the sampling number per second is 3×106,that is,the fast time sampling rate Fs; and the total number of sampling points is 128,which is represented by M.Since Fsis much larger than fs,1/ Fscan be ignored compared with 1/ fs.Then (6),that is,the echo signal to be processed after sampling can be approximated in the form of the matrix as follows

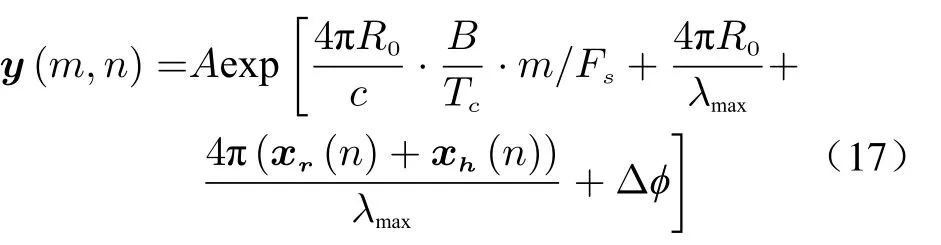
where y(m,n) is the echo signal to be processed after sampling,Fsis the fast time sampling rate,Δφ is the phase noise,m=0,1,2,...,M–1,and the parameter R0is the location of the human target,which is set according to Tab.2.λmaxis c alculated from fmin.

3.2 Results Analysis

3.2.1 Precision Analysis of Range Bin Selection The echo signal reflected by a human target with a distance of 1.4 m from the radar is simulated.Fig.3 shows the range window of the target obtained after direct FFT and improved DFT processing for each chirp respectively.By comparison,it can be seen that the result of the direct FFT algorithm is 1.406 m,and the result of the improved DFT algorithm is 1.401 m,which verifies the high-precision performance of the latter.

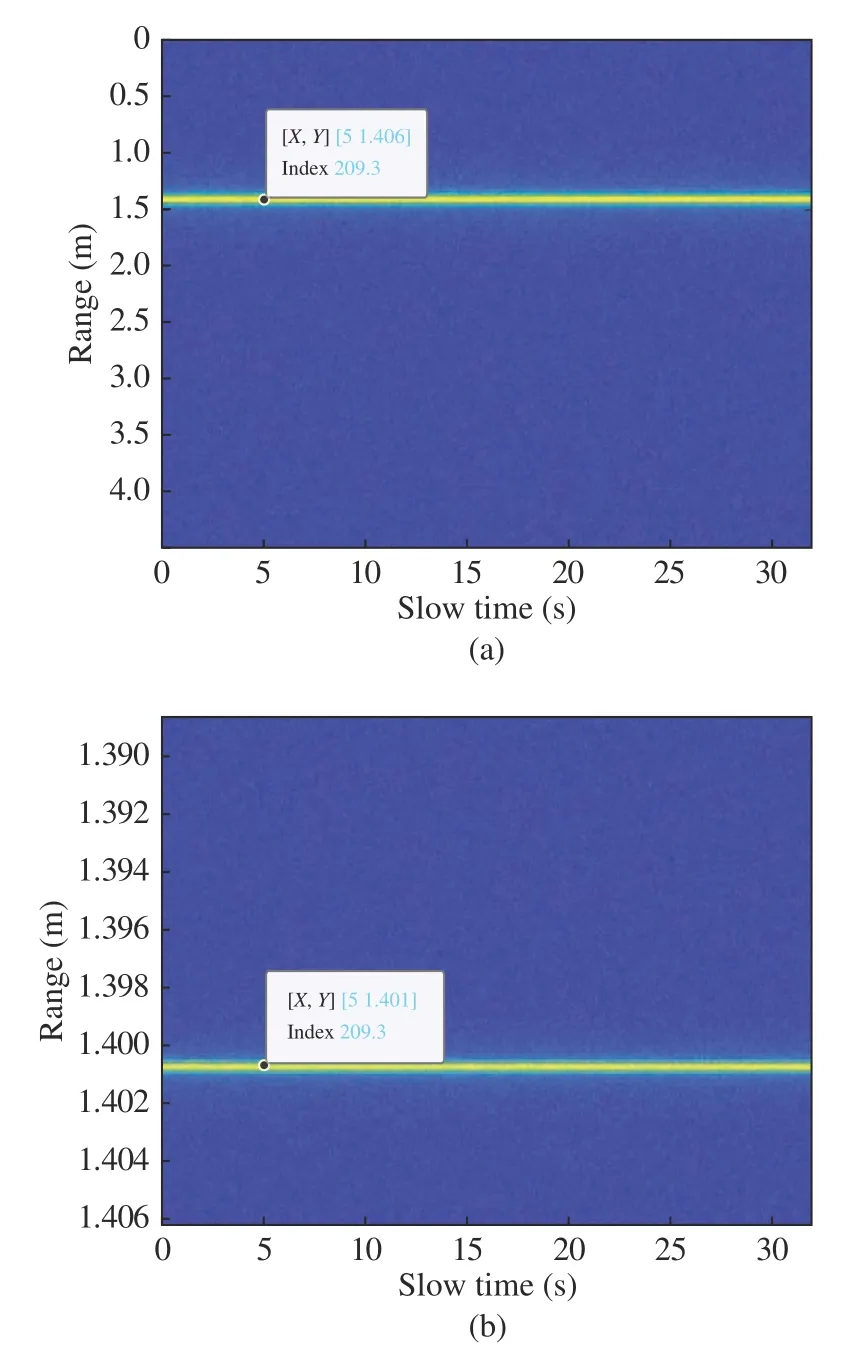
Fig.3 Target range window:(a) FFT;(b) improved DFT

3.2.2 Recovery Effects of Respiratory and Heartbeat Signals

Cardiopulmonary signs were constructed according to (16) and Tab.2,as shown in Fig.4.Fig.5 shows the phase information contained in the range window of the target extracted from the simulated echo signal by phase unwrapping and extended DCMA method.The phase here refers to the phase of the echo signal,which includes respiratory rate and heart rate information.And the horizontal axis in Fig.5 refers to the slow time category.It can be found that after phase unwrapping,there is still a lot of high-frequency interference information in the phase signal,from which it is difficult to extract respiratory and heartbeat signals.The extended DCMA method basically realized the signal recovery and laid a foundation for the subsequent estimation of respiratory and heartbeat frequency.

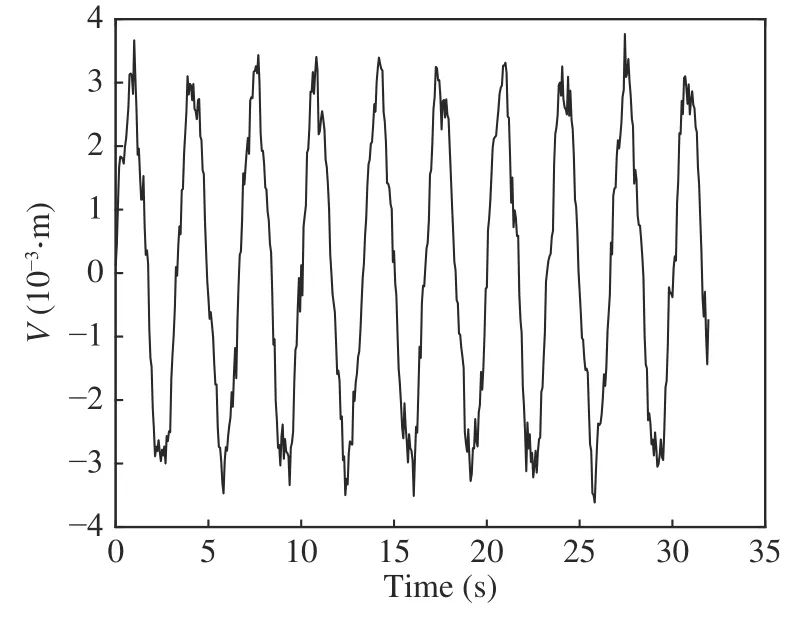
Fig.4 Simulated physical signs

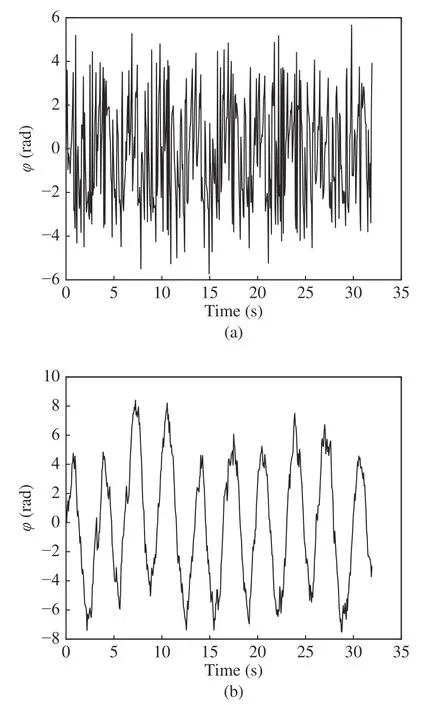
Fig.5 Recovered breathing and heartbeat signals:(a) phase unwrapping;(b) extended DCMA method

3.2.3 Analysis of Frequency Estimation Results Fig.6 shows the amplitude spectrum obtained by direct FFT of cardiopulmonary signals recovered by the extended DCMA method.It can be found that the frequency of respiratory signals is estimated to be 0.312 5 Hz at this time,and the relative error is 4.17%.In addition,there is low-frequency noise interference and the respiratory signal covers up the heartbeat information.

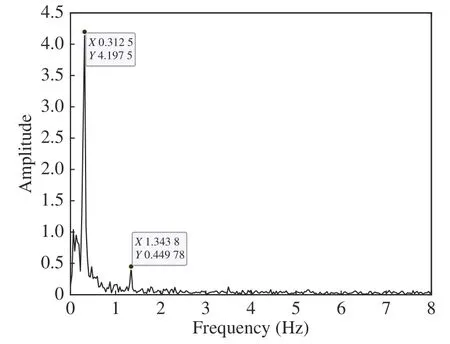
Fig.6 FFT amplitude spectrum of the recovered signal

Fig.7 shows the signal waveform and spectrum after the high-pass filter removes low-frequency information,where the first piece of the graph shows the waveform in Fig.5(b),the second piece shows the amplitude-frequency response of the designed high-pass filter,the cutoff frequency of which depends on the measurement to the breathing rate,and the third and the fourth pieces of the graph respectively show the waveform and corresponding spectrum of the original signal (as shown in the first picture)filtered by the high-pass filter.It can be found that the low-frequency part is basically filtered out,reducing the impact on heart rate measurement.However,it is not difficult to find that the amplitude of some spectral lines in the amplitude spectrum is basically the same as the spectral line corresponding to the heartbeat frequency.After analysis,this part of the spectral line is the harmonic component of breathing.The signal shown in the third part of Fig.7 is filtered through the notch filter bank to obtain the finally recovered heartbeat signal.And the first part of Fig.8 is the time-domain signal obtained by this step,while the second part is its spectrum.By observing its amplitude spectrum,we can find that the heartbeat signal is basically restored.

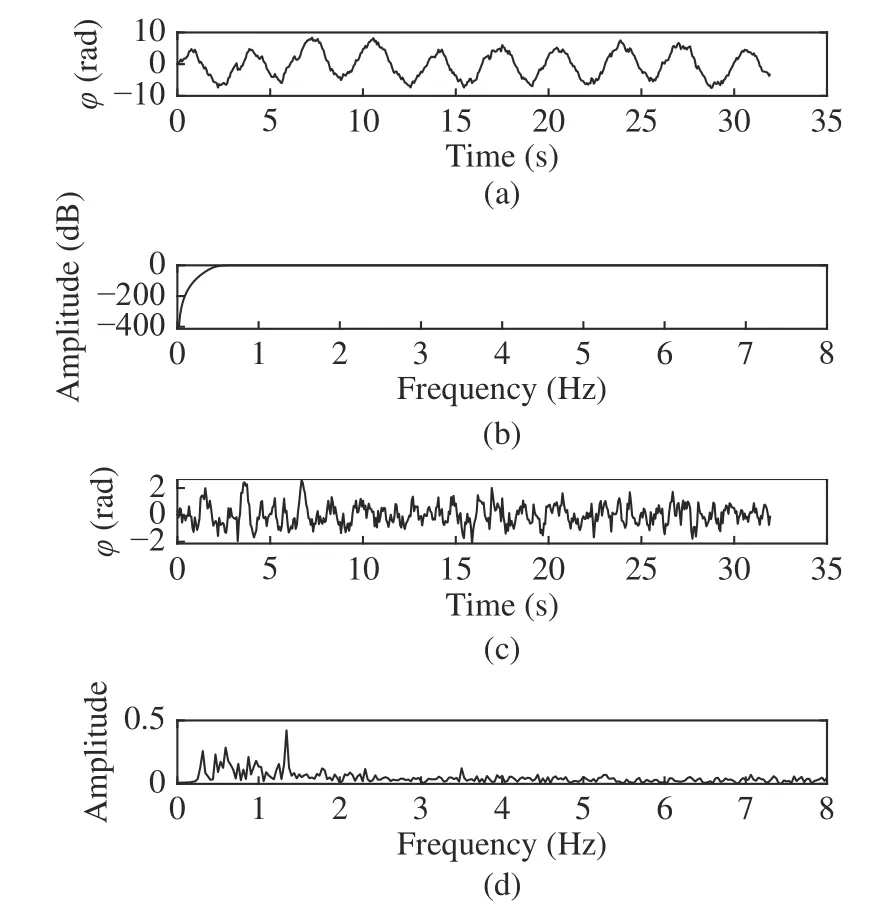
Fig.7 Filtering effect of high pass filter:(a) original signal;(b) high pass filter;(c) filtered signal;(d) FFT

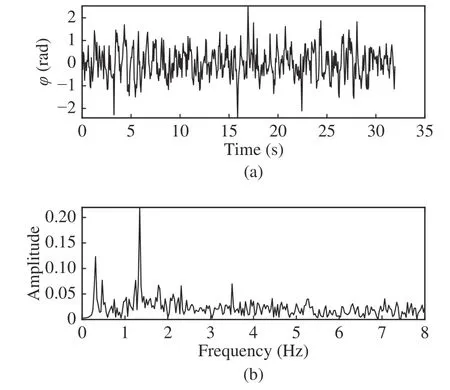
Fig.8 Filtering effect of notch filter banks:(a) filtered signal;(b) FFT

CZT calculation was performed on the restored cardiopulmonary signals as shown in Fig.5(b) and the restored heartbeat signals as shown in Fig.8,and the results are shown in Fig.9,where the respiratory and heartbeat frequencies are 0.300 5 Hz and 1.349 9 Hz respectively.Tab.3 compares the results obtained by the direct FFT method and CZT algorithm,where the relative error is expressed as the ratio of the difference between the simulation value and the theoretical value to the theoretical value.It can be found that the accuracy of respiration and heart rate has been greatly improved.

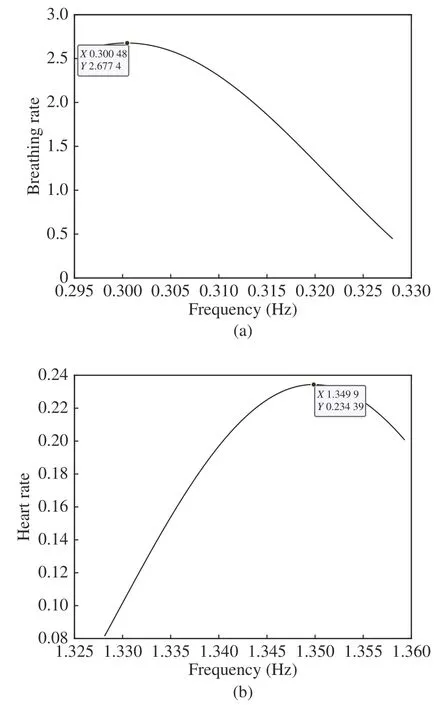
Fig.9 CZT algorithm results:(a) respiratory signal;(b)heartbeat signal

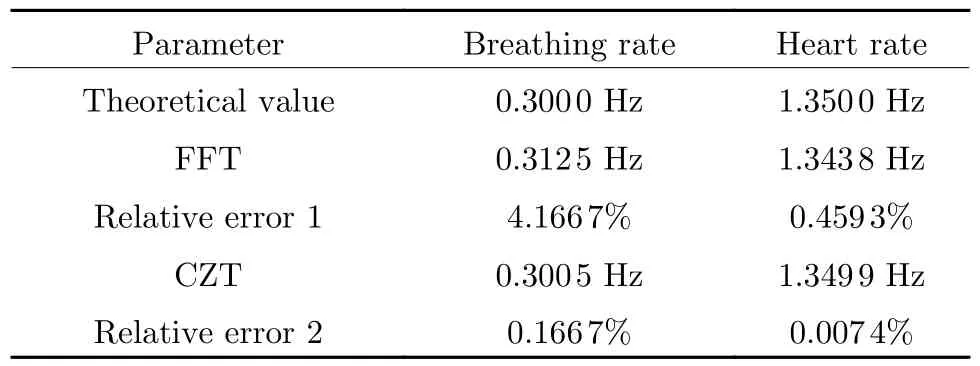
Tab.3 Comparison of accuracy

Tab.4 lists two extreme conditions within the range of normal cardiopulmonary frequencies.One is a relatively low respiratory rate with a relatively high heart rate,and the other is a relatively high respiratory rate with a relatively low heart rate.After verification,it is found that the relative error can be kept below 1.5% in the two cases,which proves the stability of the proposed algorithm in high precision frequency estimation.

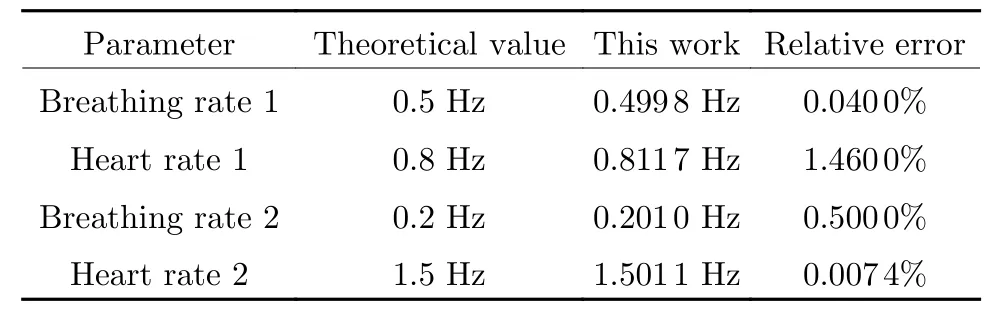
Tab.4 Accuracy realization of different cardiopulmonary signs

Tab.5 shows the comparison of relative errors of the respiration and heart rate obtained by different algorithms.These algorithms are based on the approximate operating frequency band in this paper.In [5],an 80 GHz ultra-wideband FMCW radar system with a bandwidth of 10 GHz was used to measure cardiopulmonary frequencies.The proposed algorithm puts forward high requirements on bandwidth.And the algorithm adopted in [13] has a relative error that is hard to ignore in heart rate detection.In comparison,the hybrid algorithm proposed in this paper is more accurate in detection.

Tab.5 Comparison of different algorithms

4 Conclusion

In this paper,based on the analysis of the spectrum refinement effect achieved by the improved DFT method and CZT algorithm,different spectrum refinement methods have been used to extract the physical signs information many times,and high accuracy has been obtained in the selection of range window and the extraction of cardiopulmonary frequency.At the same time,the extended DCMA algorithm can realize breathing and heartbeat signals recovery more effectively than the commonly used phase unwrapping method.In addition,notch filter banks with very narrow stopband bandwidth are used to overcome the interference of respiratory harmonics on heartbeat signal.Finally,the relative error of frequency estimation can be kept below 1.5%,which verifies the feasibility of the proposed method.