航空发动机多元拉杆结构载荷标定试验技术
2022-03-02田常棵王培元安中彦吴法勇项钧清
田常棵,苏 军,王培元,安中彦,吴法勇,项钧清
(中国航发沈阳发动机研究所,沈阳 110015)
在航空领域中,安装系统是指将航空发动机安装在飞机上所需的机械构件系统,其功能是将发动机推力和各种附加载荷传递给飞机,保证发动机在整个飞行包线内能够可靠定位、安全连接。发动机安装系统承载大、工况状态多,对安装系统进行准确的受力状态测量是保证其工作安全及发动机工作状态确认的重要措施,而拉杆结构是发动机安装系统中常用的受力构件,对其进行实际工作时的受力状态测量是保证其安全工作的重要措施。
本文研究了基于多元承载设计的航空发动机多元结构拉杆试验件的载荷标定试验技术,其应变测量位置与承受载荷的应变-载荷曲线呈现出线性段与非线性段结合的曲线特征。为提高其载荷标定精度,分别研究了应变片粘贴位置、应变数据稳定性、加载位置偏移及装配扭矩对载荷标定精度的影响,从而确定更好的载荷标定测量方案。
1 多元拉杆结构载荷标定试验方法
1.1 载荷标定试验方案
如图1所示,某型航空发动机辅助安装节多元拉杆结构由2个侧拉杆、1个中间拉杆、2个连接销及其拧紧螺母组成,其单耳侧及双耳侧的两端与关节轴承相连,因此多元拉杆结构在工作中为二力杆受力结构,仅需对其进行拉压载荷的标定,本文仅就其在承受拉伸载荷时进行讨论。
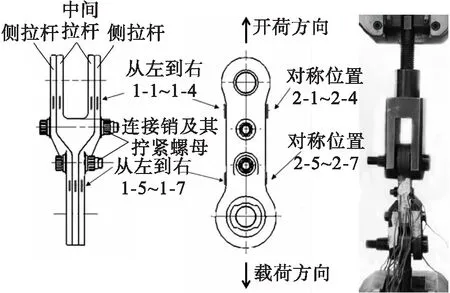
图1 多元拉杆结构及载荷标定试验方案图
为了确定合适的应变片粘贴位置,使用ABAQUS有限元软件分析了多元拉杆结构在拉伸载荷方向上的应变云图(拉伸载荷为80 kN,螺栓预紧力为2 000 N),如图2a所示。根据应变云图分析,多元拉杆结构的单耳侧及双耳侧具有较大的应变值,适合载荷标定,应变片粘贴位置及编号如图1深色短线所示。通过有限元软件分析了应变片粘贴位置处的应变-载荷曲线,此应变-载荷曲线为非线性曲线,如图2b所示。
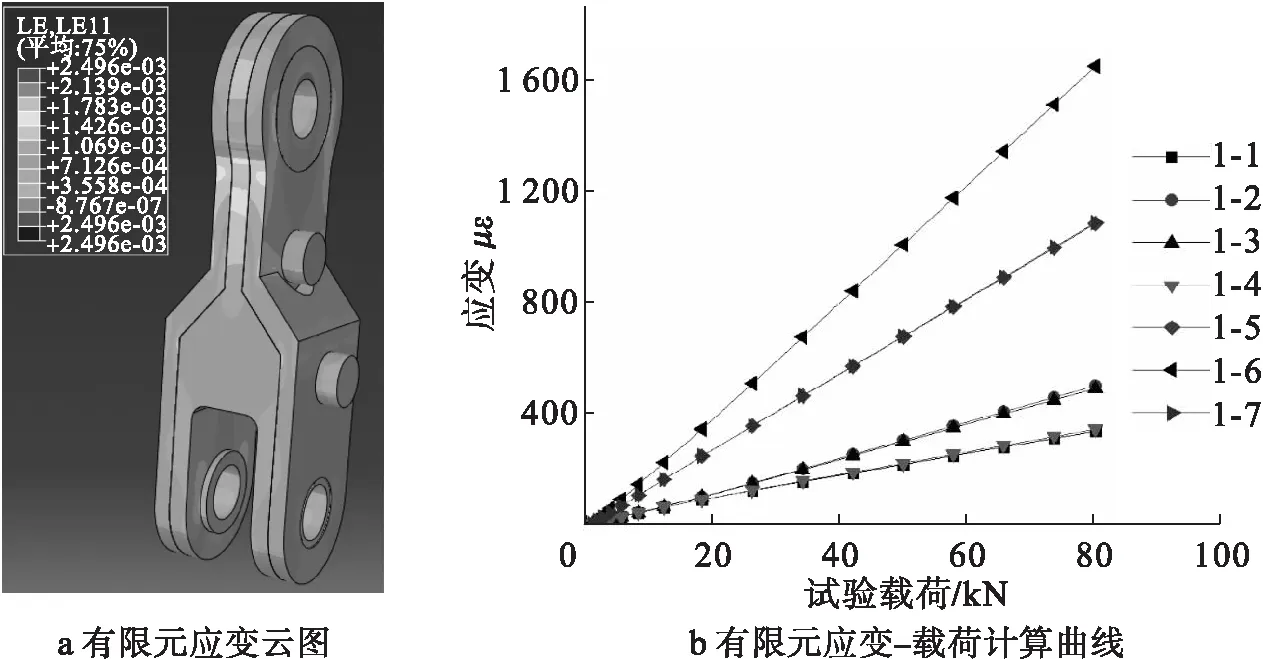
图2 有限元应变云图及应变计算结果
3个拉杆之间的非线性接触是造成应变片粘贴处应变-载荷曲线非线性的重要原因,中间拉杆双耳侧承受载荷比例随加载载荷变化的曲线如图3所示。从图3可知,其承受载荷比例随试验载荷的增加而增大,这是由于侧拉杆受拉向载荷作用时,其变形趋势为在长度上变长、在厚度上变薄(如图4所示),其变形趋势导致随着试验载荷的增加,侧拉杆在斜接触面上对中间拉杆的接触力越来越大,造成中间拉杆承受了更大比例的拉向载荷,并在应变上反映出其随载荷非线性变化的特征。
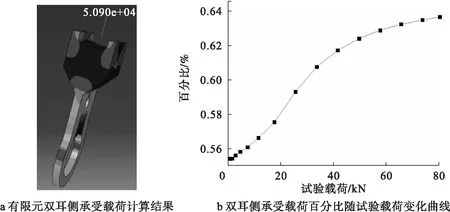
图3 中间拉杆双耳侧承受载荷比例随载荷变化曲线
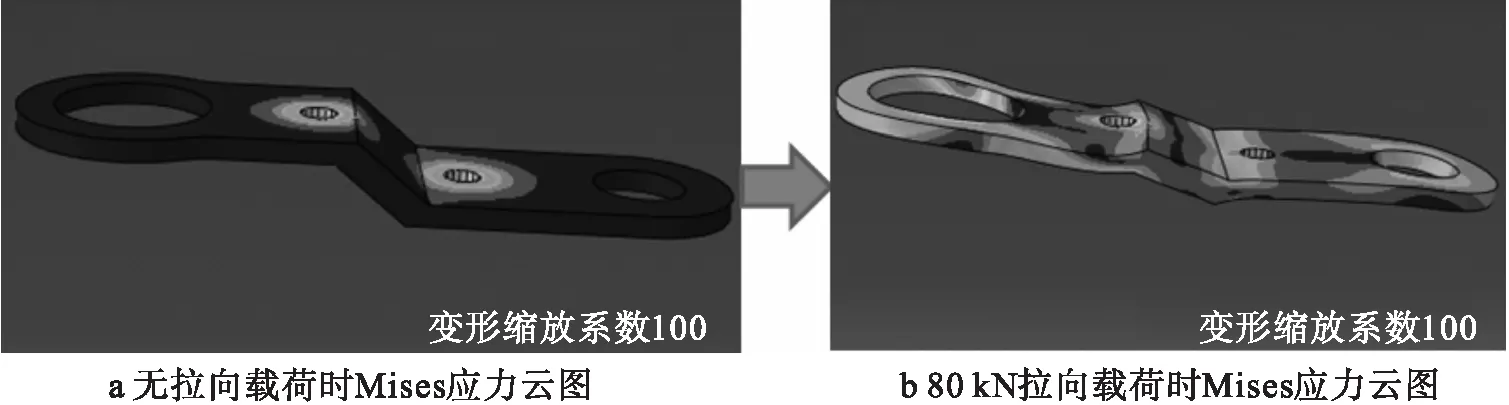
图4 侧拉杆受拉向载荷作用时变形趋势图
1.2 拉杆结构典型应变-载荷曲线
通过有限元分析及考虑应变片布局,结合工程使用的方便性(可将应变片串联,直接测量其应变和),可使用多元拉杆结构的单耳侧中间拉杆应变和(1-6、2-6应变片之和,数值意义为其平均应变值的3倍)、双耳侧中间拉杆应变和(1-2、1-3、2-2、2-3应变片之和,数值意义为其平均应变值的4倍)、单耳侧应变片和(1-5~1-7、2-5~2-7应变片之和,数值意义为其平均应变值的6倍)或双耳侧应变片和(1-1~1-4、2-1~2-4应变片之和,数值意义为其平均应变值的8倍)共4种应变片组合测试方案作为载荷标定的应变值,多元拉杆结构载荷标定的典型应变-载荷曲线如图5所示。从图5可知,相较于将曲线整体拟合为二次多项式,将曲线作为2段分段函数进行拟合的效果更好,即在0~30 kN呈现出抛物线变化趋势,可采用二次多项式拟合,在30~80 kN为线性变化趋势,可采用线性拟合。

图5 拉杆结构典型应变-载荷曲线
2 载荷标定影响因素分析
由于拉杆为多元结构组合件,具有非线性接触的特点,根据其载荷标定或实际使用状态,分析了多次加载中应变数据的稳定性、加载位置偏移及连接销拧紧力矩对载荷标定应变数据的影响;同时,也分析了这些因素对4种应变片组合测试方案的影响,以找到其中最好的应变片组合测试方案。
2.1 多次加载中应变数据的稳定性分析
能否将应变标定数据用于试验中的载荷测试,需考虑多次加载过程中应变数据的稳定性问题,以及拟合曲线计算出的应变值与试验测得应变值的精度问题。
连接销拧紧力矩为20 N·m时,试验载荷加载到80 kN并卸载后的残余应变变化图如图6所示。首次加载并卸载后,应变片有较大的卸载残余应变,继续进行3次加载试验,加载后卸载的残余应变很小,可忽略残余应变的影响。
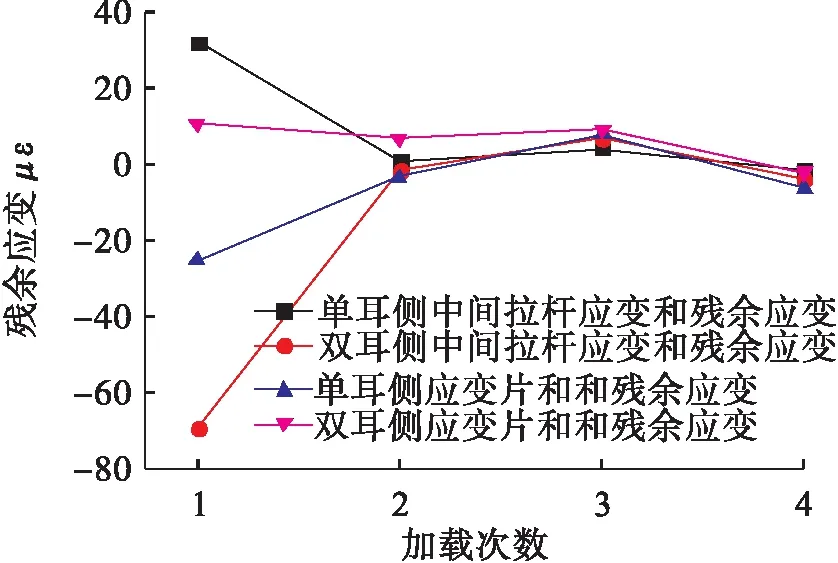
图6 残余应变随加载次数变化图
在连接销拧紧力矩为40 N·m时,对第2次载荷加载的试验数据进行应变-载荷曲线拟合,并将此拟合曲线作为基准,计算第2~4次载荷加载时试验数据与拟合曲线的偏差,以分析此拟合曲线的精度及第2~4次载荷加载时应变数据的稳定性,试验数据与拟合曲线偏差统计图如图7所示。由图7可以看出,4种应变片组合测试方案的试验数据与拟合曲线偏差在±2.5%以内,当载荷大于30 kN时,采用4种应变片组合测试方案进行曲线拟合时具有较高的精度;同时发现,单耳侧应变片和拟合曲线计算出的应变值与试验测得应变值的偏差均在±1%以内,因此采用单耳侧应变片和作为载荷标定应变值时,其全部载荷区间范围内均具有较高的精度。同时可以看出,对第3次、第4次的试验数据使用第2次载荷加载的拟合曲线进行载荷标定时,其偏差无较大变化,说明后续加载应变数据具有很好的稳定性,因此可将首次加载作为预加载后,使用后续应变标定数据进行校准曲线拟合,用于试验中的载荷测试。
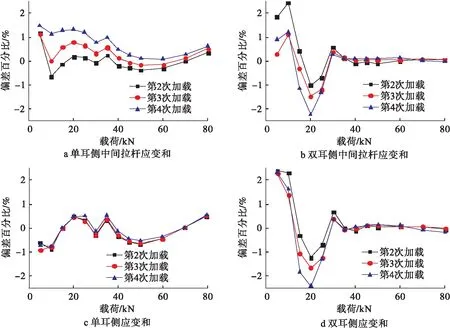
图7 第2~4次加载时试验数据与拟合曲线偏差统计图
2.2 加载位置偏移对载荷标定的影响
由于多元拉杆结构的载荷标定试验工装结构相较于其实际连接结构有一定差异,尤其是使用的标定试验工装为有安装间隙的试验工装结构时,容易在载荷标定过程中出现加载位置偏移拉杆中面的情况,需分析加载位置偏移拉杆中面对应变标定数据的影响。
表1为连接销拧紧力矩为40 N·m时,在80 kN载荷下(已预加载),以未偏移的应变测量值为基准,拉杆双耳侧加载中心偏移拉杆中面的位移为2 mm和4 mm时应变标定数据相对于基准的应变偏差统计表。从表1可以看出,当双耳侧的加载位置偏移拉杆中面时,双耳侧中间拉杆应变和、双耳侧应变和的应变结果偏差较大,达到了±2%以上;单耳侧中间拉杆应变和、单耳侧应变和影响较小,在±1%以内。从材料力学上分析,由于双耳侧应变片粘贴位置距离中面较远,因此在相同弯矩的影响下,其应力、应变水平变化更大。从试验过程中可能出现加载位置偏移拉杆中面的情况分析,单耳侧中间拉杆应变和、单耳侧应变和更适用于应变载荷标定。

表1 应变标定数据相对于基准的应变值偏差统计表
2.3 连接销拧紧力矩对载荷标定的影响
多元拉杆结构由2个侧拉杆和1个中间拉杆通过2个连接销及其拧紧螺母拧紧组成,连接销附近的受力状态会影响多元拉杆整体结构的受力状态,螺纹连接紧度受疲劳载荷、温度变化等因素影响时,连接销的拧紧力矩容易发生变化,因此需要分析连接销拧紧力矩对应变数据的影响。
图8为在80 kN载荷下(已预加载),以连接销拧紧力矩40 N·m为基准,应变值随连接销拧紧力矩的变化统计图。由图8看出,单耳侧中间拉杆应变和、双耳侧中间拉杆应变和受连接销拧紧力矩的影响明显,偏差达±2%以上;而单耳侧应变和、双耳侧应变和受连接销拧紧力矩的影响较小,偏差为±1%以内,受拧紧力矩的影响更小。
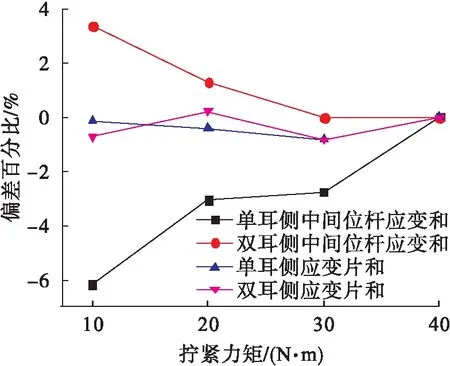
图8 应变偏差随拧紧力矩的变化统计图
3 结论
(1)多元拉杆结构载荷标定的典型应变-载荷曲线为非线性曲线,为提高载荷标定精度,可将曲线作为2段分段函数进行拟合;
(2)当改变连接销拧紧力矩首次加载时,应变片有较大的卸载残余应变,因此应使首次加载作为预载,后续加载应变数据具有很好的稳定性,可将后续应变标定数据作为标定载荷的应变输出结果,用于试验中的载荷测试;
(3)在拟考虑的4种应变片组合测试方案中,采用单耳侧应变片和作为载荷标定应变值具有较高的载荷标定精度,其拟合曲线计算出的应变值与试验测得应变值的偏差在±1%以内,其受加载位置偏移及连接销拧紧力矩的影响的偏差也在±1%以内,满足工程使用要求。
