基于流体网络法的射流式风洞系统流动计算分析

孙 科，张久峰，刘 涛，梁靖国，宋江涛

(1.中国飞行试验研究院 发动机所，西安 710089；2.西安远方航空技术发展有限公司，西安 710089)

风洞试验是一种在空气动力学研究领域应用广泛的研究方法，其具有试验数据精度高等优势,是仿真分析等方法无法比拟的。航空发动机流道内气动参数测量的受感部一般都需通过风洞吹风，对受感部的角度及速度特性进行验证[1]。五孔探针等多孔探针使用前都需进行不同速度、不同气流偏角条件下的吹风校准，测量结果结合校准曲线可得到气动参数。受感部气动吹风校准一般采用下吹式自由射流风洞[2-3]，按照相关标准要求总静压复合受感部和多孔方向受感部均应进行吹风校准[4-5]。因此，风洞试验在受感部气动吹风校准方面具有十分重要的作用。下吹式自由射流风洞由气源系统、扩散段、稳定段、收缩段及试验段组成。气源系统产生高压气体，为风洞运行提供基本工作介质，气体从高压端持续向低压端流动，经过收缩段加速后，气流自由射流进入环境空间中。吕聘予等[6]进行了低速高温风洞结构设计及性能测试；王文奎等[7]进行了风洞洞体设计。风洞设计时需考虑沿程损失及稳定段中阻尼网与蜂窝器形成的局部损失，综合考虑风洞系统各环节的流阻特性，为气源系统的选型提供指导。李勇等[8]针对其设计风洞中的收缩段，采用数值模拟进行仿真计算，得到收缩段及试验段速度变化。孔诗媛等[9]设计了气象用强风风洞，利用总当量损失系数计算风洞能量损失。张洪军等[10-11]设计了风冷散热器测试风洞，采用并联工作的两台风机作为气源，并采用总等效阻力系数对流阻进行评估。姚家平[12]设计的风洞用储气罐作为气源，在能量损失评估时将不同元件间的损失系数进行叠加。现有研究[13]虽考虑风洞系统中不同部件的阻力损失，但将流阻等效为局部阻力损失系数，将不同部件阻力系数简单相加，得到系统总阻力，结合试验段气流动压头，得到系统压降。这种方法仅可大致估算系统损失，不能精确评估，如采用CFD对风洞系统流阻特性进行研究，所耗费计算资源较大，时间较长。

孙科等[14]将流体网络法应用于管路系统流阻计算分析，对风洞系统的流动阻力进行评估分析。本文将风洞系统简化为由等截面摩擦管、扩散段、蜂窝器、阻尼网、收缩段等关键部件组成的系统，各个部件的阻力分别在当地气流速度条件下精确计算。通过分析计算，揭示气流在风洞系统中的流动过程及原理，了解风洞系统内部流动损失机理，为气源系统设计选型提供精确指导，为试验段气流速度预评估提供数据支撑。

1 风洞系统介绍

1.1 风洞系统组成

射流式风洞系统一般由气源系统、扩散段、稳定段、收缩段及试验段等组成，如图1所示。气源系统为风洞提供所需的压缩空气，型号为雷茨Explorer-350风机，风机出口最大总压的表压值达38 kPa，该型风机可持续为试验段提供所需的压缩空气。扩散段对气流进行减速扩压，并逐渐过渡至稳定段中。稳定段削弱气流紊流度，并使气流更均匀，其内一般布置蜂窝器及多层阻尼网。在收缩段中气流增速减压，并膨胀至试验段。受感部气动吹风校准使用下吹式自由射流风洞开展，其试验段为开口式设计，气流直接膨胀至大气环境中。

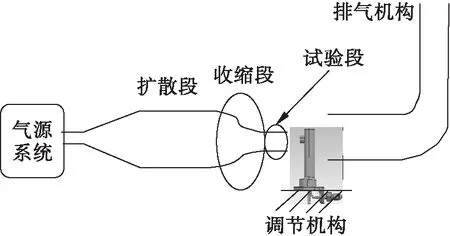
图1 射流式风洞示意图

气源系统产生的高压气经过一系列损失之后，气流总压降低，所以在风洞结构设计初期，需考虑气源系统的选型设计，且需评估试验段气流所能达到的速度。通过评估风洞系统所产生的损失，计算得到试验段气流速度。

本文所设计的风洞主要针对气动探针校准，因此试验段内径设计为100 mm，在收缩段后等截面延伸50 mm，在该延伸段布置静压测点。扩散段入口为100 mm的等截面管。收缩比设置为16，稳定段内径为400 mm，稳定段从上游至下游分别布置1层蜂窝器及8层阻尼网。在蜂窝器前、后各留300 mm的管段，在8层阻尼网后预留400 mm的静流段，使气流湍流度进一步减弱，并布置总压测点。

1.2 流体网络模型

应用流体网络法将风洞系统简化为典型元件组成的流体网络，各个元件代表风洞系统中的部件，各个元件均有明确的计算方法，可得到整个系统的压力损失及试验段气流速度。图2为射流式风洞的流体网络结构图。

图2 射流式风洞的流体网络结构图

气源系统选用了雷茨Explorer-350风机，其在某一工作状态下可长期稳定工作，可为风洞系统提供所需的压缩空气，保证风机出口气流的总压及总温恒定。将风机出口作为整个流体网络的入口，首先气流流过一段管路，对应管元件；随后经过稳定段上游的扩散段，气流增压减速，对应局部损失元件(突扩损失)；再进入稳定段内的等截面管段，对应管元件；随后经过蜂窝器，对应局部损失元件；在蜂窝器后气流在等截面管段流动，对应管元件；随后进入8层阻尼网，对应8个局部损失元件；后经过收缩段，气流膨胀至大气环境中，流速加快，对应局部损失元件(突缩元件)。风洞出口为大气压力环境，出口条件明确。

表1为流体网络中各个元件类型与实物对应情况及各个元件进出口节点编号。整个流体网络中空气由入口流入，后经过扩散段前的管元件，再经过扩散段，进入蜂窝器前的等截面管中，通过蜂窝器进入蜂窝器后的等截面管中，后进入共8层阻尼网形成的局部损失元件，再流经阻尼网后的等截面管内，最后经过收缩段对应的局部损失元件，收缩加速。

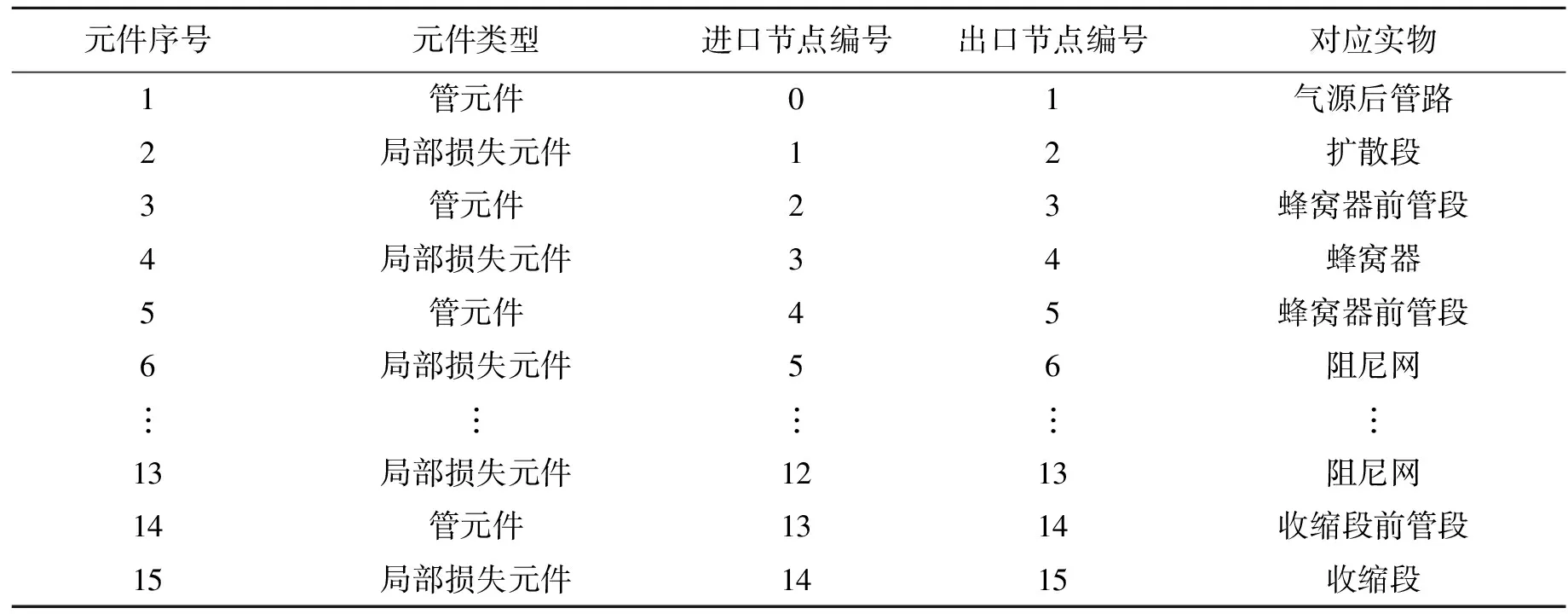
表1 流体网络元件与实物对应关系

2 典型元件计算方法

2.1 等截面摩擦管流

风洞系统中的气流流动时间尺度远远快于气流与管路壁面间的壁面间传热的时间尺度，对气流与壁面间的传热可忽略不计。管元件内部流动原理为等截面摩擦管流在气流膨胀、壁面摩阻及边界层充分发展的作用下，气流加速运动。图3所示为在等截面管微元段中的流动示意图。

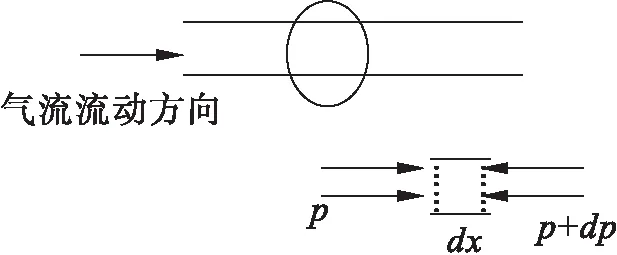
图3 等截面管微元段

式(1)为等截面摩擦管流在微元段上的总压差计算式，其与气流马赫数及壁面摩阻、管路直径有关

(1)

其中：p*为气流总压，单位为Pa；dp*为在微元段上的总压差，单位为Pa；k为绝热指数，对空气为1.4；Ma为气流马赫数；Cf为壁面摩阻；dx为微元段长度，单位为m；d为等截面摩擦管的管径，单位为m。

将式(1)进行转化后得到总压随管长度方向的变化关系。

(2)

使用Runge Kutta法[13]求解式(2)所示的常微分方程。

由于等截面摩擦管流与外界没有机械功或热的交换，在给定的边界条件下，即给定入口总压、入口总温、流量，便可得到等截面摩擦管流沿程的总压分布。根据式(3)，通过总压、流量、总温，便可得到气流马赫数及气流速度、气流静温、气流静压等参数。

(3)

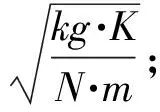
(4)

2.2 扩散段

在稳定段内部前端设计扩散段，从而将气流从较小尺寸的管径扩散至较大横截面的稳定段，进而减少气流在扩散段内的能量损失。

在没有分离的情况下，气流通过扩散段的损失ΔP主要包含摩擦损失和扩压损失两种，可用式(5)表示

(5)

其中：A1和A2分别是扩散段进口、出口截面积；q1为进口截面动压值；λ平均为摩擦损失系数；θ为扩散段全扩散角。

由式(5)可知，最少损失时的最佳扩散角θ可按式(6)计算，λ平均≤0.01，则可得最佳扩散段的扩散角θ≤5°。

(6)

2.3 蜂窝器

为使气流均匀，并且降低紊流度，需在稳定段中安装蜂窝器及纱网等结构。稳定段直径直接关系到风洞的收缩比C，即稳定段截面积与试验段截面积之比。随着收缩比C的增大，气流在稳定段的流速将明显降低，使得气流在通过稳定段内各整流装置(蜂窝器、阻尼网)时的压降也相应降低。

按照试验段直径为100 mm进行设计，取收缩比值为16，则稳定段直径为400 mm。

蜂窝器长细比为15，损失系数一般较大。蜂窝器的损失包括入口损失Km、摩擦损失Kf和出口损失Kout，即：

K=Km+Kf+Kout

(7)

其中3种损失的计算表达式分别为式(8)、式(9)、式(10)。

(8)

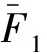
(9)

其中：λ为摩擦阻力系数；L为蜂窝器长度，单位为m；D为蜂窝器水力直径，单位为m。

(10)

2.4 阻尼网

对阻尼网而言，当网丝雷诺数大于1 000时，其损失系数可按照下式[15]计算

(11)

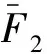
2.5 收缩段

收缩段使稳定段的气流均匀加速后进入试验段，湍流度降低。收缩段的收缩曲线应使流速沿轴向均匀地增加，不产生边界层分离现象；在收缩段的入口和出口处，壁面平行于风洞轴线，保证出口截面气流的速度均匀，方向和风洞轴线平行。稳定段的横截面积与试验段的横截面积之比称为收缩比。在试验段横截面积和气流速度大小一定的条件下，如果收缩比取值大一些，可以降低稳定段的气流速度，从而使稳定段和整流装置改善流场品质的作用发挥得更好，而且气流的能量损失也要小一点。选用式(12)所示的韦氏曲线进行收缩段的设计，研究表明，这种曲线型面造成的损失系数很小。

(12)

其中：R1为收缩段进口截面半径,单位为m；R2为收缩段出口截面半径,单位为m；x为距离收缩段进口截面的距离,单位为m。

3 计算及分析

在建立流体网络模型的基础上，设计风洞系统各个关键元件的结构尺寸，试验段出风口直径为100 mm。结合上述的各个元件流动计算方法，分析风洞系统流动损失。

3.1 风洞系统压力损失分析

气源压力即入口节点总压为126 kPa，试验地常年大气压力为96 kPa,即出口节点静压为96 kPa。由于风洞系统中选用的风机工作过程基本为等熵压缩过程，在对气流做功使得气流总压升高的同时，气流总温也升高，设置入口节点总温为333.15 K，风洞系统为绝热系统。根据上述条件设置基本算例中流体网络的入口及出口参数进行工程计算。

图4为沿程各个节点总/静压的计算结果。结果显示，由入口至出口间气流总压逐渐减小，体现了风洞系统中各个元件造成的损失，且沿程各个节点上的静压均比总压小。1#元件入口/出口节点静压(Ps0、Ps1)与15节点静压(Ps15)均较小，相应流通直径都较小，其中流体速度较大，总压与静压差较大。图5为沿程各个节点静温及流速计算结果，其与静压结果趋势基本一致，节点1、节点2、节点15的静温较小，对应的气流流速较大。计算结果显示，在稳定段内流速不足20 m/s,气流湍流度在稳定段内充分减弱。

图4 沿程总/静压计算结果

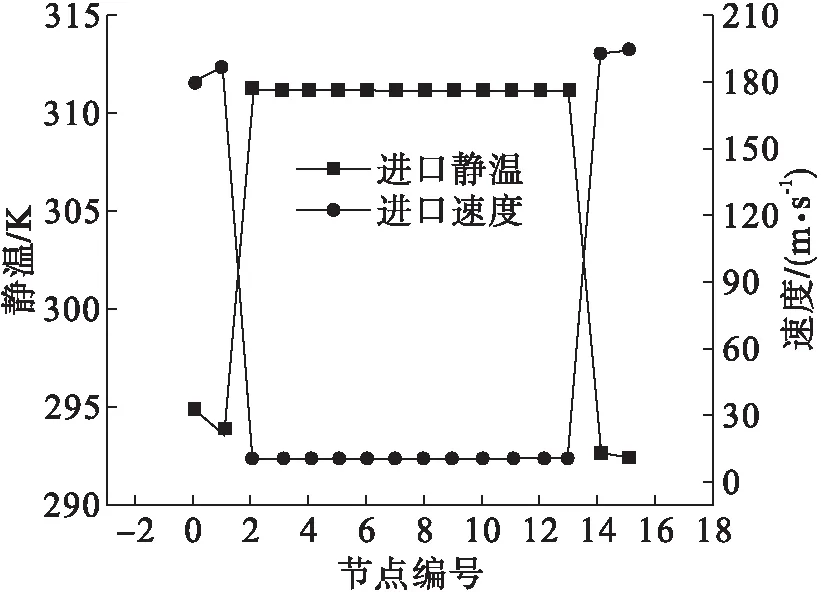
图5 沿程静温及速度计算结果

3.2 气源压力对气流速度影响

设置气源压力为不同值进行工程计算，得到不同气源压力条件下，系统流量值及试验段风速值，为试验段风速的评估及气源系统的选型提供支撑。设置入口节点全压为5～40 kPa，间隔为5 kPa，分析图6的计算结果，结合所选风机性能曲线，由于采用两台风机并联工作，图6中风机特性曲线为两台雷茨Explorer-350风机累加结果。在风机额定运行状态，设计形成的风洞系统试验段气流马赫数可达0.47。随着气源压力增大，所消耗的空气流量及试验段气流速度逐渐增大。因此，如需提升风洞试验能力，提高试验段气流速度，需同时提升气源系统增压能力及气源系统供气流量。

图6 空气流量及试验段马赫数随入口全压变化情况

3.3 试验段直径影响

针对不同试验段直径进行计算，分别设置试验段内径为80 mm、120 mm，与基本结构100 mm进行对比,各种不同直径试验段下的收缩比均设置为16。由于试验段为整个风洞系统中流通面积最小部位，因此其内径直接决定了风洞的流阻特性。在相同入口全压下，随着试验段直径的增大，风洞所需的空气流量逐渐增大。使用同一个风机为不同尺寸风洞提供风源时，由于不同风洞流阻特性不同，导致风机额定状态下的工作点不同。图7中各风洞流阻特性曲线与风机特性线的交点即为风机工作点。随着试验段直径增大，入口全压减小。图8为不同尺寸风洞下马赫数随入口全压变化情况，在相同入口全压情况下，随着试验段直径增大，试验段马赫数略有增大，这是由于管路直径越大，流动阻力损失越小。

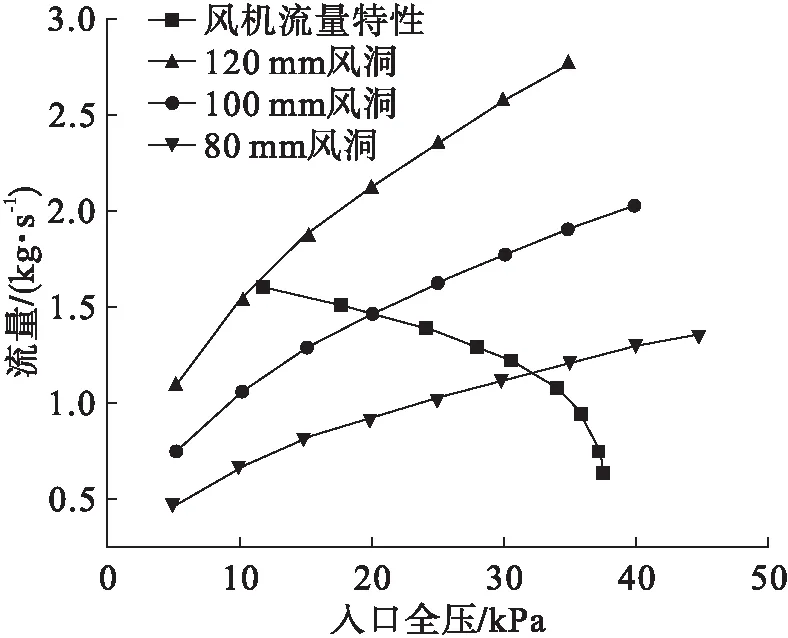
图7 不同尺寸风洞流量特性对比

图8 不同尺寸风洞马赫数随入口全压变化情况

由于风机额定工作状态下，直径较大的风洞入口全压较小，对应的直径较大风洞试验段速度较小。对于所选风机，随着风洞试验段直径增大，试验段速度减小。表2为不同设计结构和风机额定运行条件下，空气流量及试验段马赫数计算结果。综合考虑后，选择试验段直径为100 mm，风洞吹风区域大小适中，适用于探针气动校准，试验段马赫数可达0.47。

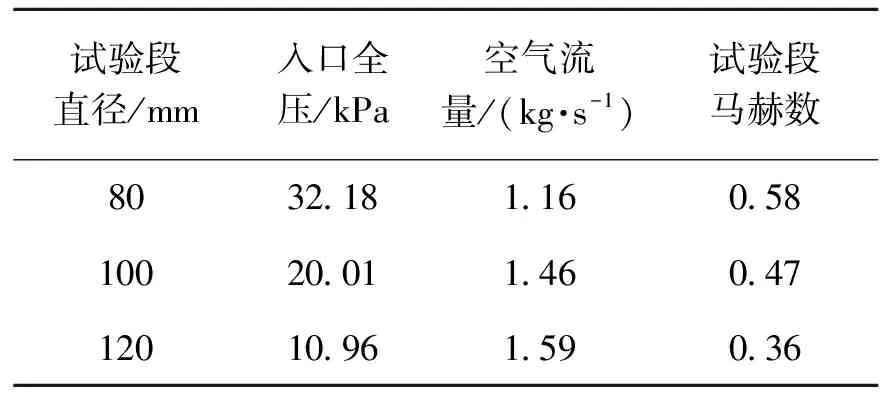
表2 空气流量及试验段马赫数计算结果

4 结论

本文针对下吹式自由射流风洞进行流动损失分析计算，揭示流动过程损失规律，探索影响试验段气流速度的影响因素。主要得到以下结论：

(1)下吹式自由射流风洞主要由气源系统、扩张段、稳定段、收缩段、试验段等组成，可将风洞系统简化成由典型元件组成的流体网络系统。通过流体网络工程计算得到风洞系统沿程气动参数分布情况，揭示风洞系统流动损失规律。

(2)分析典型工况下的计算结果得出，流动损失在扩张段较大，而在稳定段内较小。由于在扩张段流道横截面变化较大，而稳定段横截面较小、速度较小，因此流动损失较小。

(3)通过不同入口全压下的计算得出，随着入口全压的增大，空气流量及试验段速度都在增大，因此为提升试验段速度，入口全压和空气流量都需提高。由于常规风机在额定功率条件，随着入口全压的增大，空气流量减小。对于选定的风机，试验段直径设计为100 mm时所能达到的最大气流马赫数为0.47。计算结果可为后续提升试验能力进行气源选型提供支撑。