基于强化学习的飞机发动机健康维护
2022-03-02李永强许雪冬
王 潇,李永强,许雪冬,曲 娜
(沈阳航空航天大学 安全工程学院,沈阳 110136)
随着航空发动机运营规模的增大,其维修市场也以超出预期的速度增长。据统计,2019年全球民航飞机维修市场规模达到819亿美元。从2021年全球区域市场预测情况来看,亚太地区市场占比最高,达到32%,其次是欧洲地区和北美地区,分别占比25%和24%。目前窄体客机发动机的大修访问量已经增长了10%,并且这种增速将持续。预计未来10年,航空维修市场将达到9 000亿美元,而飞机发动机维修更是航空维修中最主要的业务。
作为飞机的心脏,航空发动机直接影响飞机的性能、可靠性及经济性,更是国家科技、工业和国防实力的重要体现。定期维护方式缺点过于明显,不仅造成资源浪费、使用效率低下,而且有时还会存在维护过剩和维护不足的情况,维护行为经常处于被动状态,维护费用也相对较高。目前,基于设备状态的维护策略研究已经吸引了全世界研究人员和工业实践者的关注,其主要思想是确定在观测的设备是否需要执行维护行动,防止设备在实际运行过程中失效或突然发生故障。应用基于状态的维护方法进行维护管理能有效地降低维护费用、提高操作安全性、降低系统故障发生的频率及严重程度。
1 研究现状
针对飞机发动机的维护问题方面,Razavi[1]提出了基于模型的航空发动机维修计划综合决策系统,最大限度地利用预计剩余时间对飞机发动机进行维护。Toufexis等[2]研究提出了涡轮叶片的剩余使用寿命的估计,展示了发动机在诊断方面的预测能力。Norcross[3]通过定性研究采用扎根理论的方法,探讨了在进行发动机维护时,如果遇到维修手册中未写到的问题时,如何采取维护决策和行动。Urdu[4]提出了飞机维修费用估算方法,该方法通过考虑老化因素,得出飞机在一定年限下的维修费用。Conijn等[5]在研究中开发了一种通用的优化方法,通过在本地减少任务间隔来系统地消除工作量过剩问题,进一步提高该应用程序的效率和通用能力。Douglas[6]建立了基于单目标代理的飞机维修管理因素模型,该模型测量了管理环境和命令对代理人动机和效力的影响。Cho[7]解决了具有低可观察性能力的飞机所特有的维修调度过程。郭翰卿[8]提出了基于可靠性的典型发动机附件维修间隔优化研究。李臻[9]探索了面向全寿命的民航发动机机队维修决策优化方法。戎翔[10]针对民航发动机的运营与维修特点,阐述了民航发动机健康管理的理念。李晓明[11]对航空发动机防喘控制系统故障预测与健康管理技术进行了研究。周媛[12]深入研究了面向民航大数据的航空发动机状态监测中的数据重构、状态监视、发动机退化模式识别以及面向大数据的系统构架和数据质量管理问题。
针对飞机发动机相关研究方法,Mahadevan[13]指出了几种异步算法之间的关键相似性,指出了哪些算法可以使平均回报最大化,并得到最优决策。Gosavia等[14]提出了一种基于策略迭代的增强学习算法,用于求解平均奖励马氏和半马氏决策问题。Kevin[15]研究了预测维护策略对制造系统的影响,发现使用基于传感器的退化模型来预测故障的好处。Gebraeel[16]建立了一个随机退化建模框架,使用的是一种计算和更新部分退化部件剩余寿命分布的方法。Niaki等[17]提出了一种基于产品质量的单阶段和两阶段决策的单机最优更换策略,主要目标是利用马尔可夫过程来确定上界和下界阈值的最优值,以使机器更换策略的总成本最小化。樊钊[18]提出了基于多维数据挖掘方法的发动机振动评级的应用研究。刘永建[19]提出了基于改进神经网络的民用发动机故障诊断与性能研究。李志鹏[20]对基于多智能体强化学习的制造过程建模进行了研究。肖嘉鸣[21]进行了深度强化学习的改进研究。彭颖[22]提出了基于退化隐式半马尔可夫模型的设备健康预测及系统性能维护策略研究。刘勤明[23]提出了基于状态检测信息的设备在线健康预测及维护优化研究。温忻[24]研究了基于深度强化学习的多智能体沟通策略。
综上所述,国内外学者对飞机发动机的维护问题采用不同的方法进行了多方面的研究。但基于飞机发动机的设备状态进行预测维护决策方面的研究仍比较欠缺,因此本文开展的相关研究具有一定的理论价值和实践意义。
2 衰变过程
2.1 衰变过程模型
在飞机发动机运行过程中,其状态由于疲劳、磨损、老化等一些原因发生衰变。有此类衰变的飞机发动机会影响飞机的安全性能,并且运营维护成本会有所提高。当飞机发动机发生衰变后,需要进行及时的维护,以确保设备能够稳定地运行,否则有可能会带来安全隐患。
本文用离散状态下的马尔科夫过程来对飞机发动机的状态进行表征,如图1所示,可以发现,飞机发动机的状态依次下降。其中,状态1、状态2、…、状态n表示飞机发动机衰变过程的各个状态。
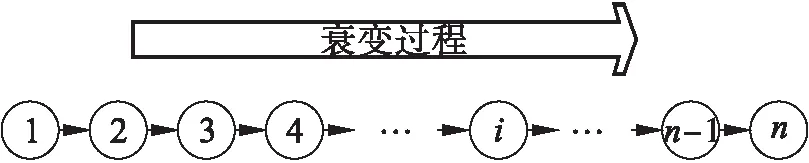
图1 飞机发动机衰变过程
2.2 观测状态信息
飞机发动机的状态水平(如1,2,…,n)不能被直接观测并准确地获取,但是通过一些可观测到的信息可以进行推断,成为设备预测维护决策的重要信息来源。而信息的获取则离不开飞机上形形色色的传感器,这些传感器构成了信息采集平台。通过传感器测量可直接得到的参数,由机载计算机计算得到间接参数,再经系统处理转变为可显示的参数,以指针、数字或图形方式显示出来,或者把这些参数传输给自动控制系统,产生控制指令,直接操纵飞机改变飞行状态。
发动机上主要的测量传感器有压力传感器、温度传感器、转速传感器、加速度传感器、迎角传感器等。传感器测量的一些参数包括风扇入口温度、LPC出口温度、HPC出口温度、LPT出口温度、风扇出口压力、涵道压力、HPC出口压力、风扇转速、转子转速、压气比、HPC出口静压、燃油流量比、修正风扇转速、修正高压轴转速、涵道比、燃气比、排气焓、需求风扇转速、需求修正风扇转速、HPT冷却流量、LPT冷却流量等。
2.3 维护决策恢复模型
(1)完美维护恢复模型设计
当飞机发动机开始运行后,随着工作时间的增加其状态不断发生衰变,并能通过监测设备的数据分析得出衰变发展情况。当达到系统设定的状态阈值W时,需要对设备进行大修,经过大修以后可以使飞机发动机恢复到之前最好的状态,如图2所示。飞机发动机在时刻t1触发大修以后,到时刻t2恢复到初始状态,这个过程称之为完美维护。其中,图2的维护时间表示为t=t2-t1,一个维护周期表示为时间t=0至t=t2。图2中的纵坐标s表示飞机发动机的完好率水平。
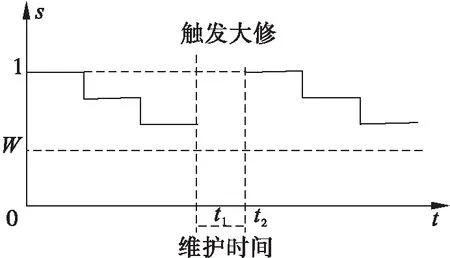
图2 完美维护
(2)不完美维护恢复模型设计
飞机发动机的不完美维护如图3所示,当飞机发动机运行到t1时刻,触发系统的第一次不完美维护,维护时间t=t2-t1,在进行维护后发现设备不能达到先前的初始状态s11,当前状态s21介于s11与s12之间;随着设备继续运行,在t3时刻又将触发设备的第二次不完美维护,维护时间t=t4-t3,在进行维护后发现设备所能达到的最优状态依然比上一次的最优状态差,即s31所处状态介于s21与s22之间。在经过几次这样的小循环后,飞机发动机的状态最终达到极限状态W,此时需要对飞机发动机进行大修,使其能够更好地继续运行。图3中,t=0至t=t6为一个大的维护周期,0-t1(k1)、t2-t3(k2)、t4-t5(k3)这几种情况称为子循环。

图3 不完美维护
在对飞机发动机进行维护时,也是属于不完美维护,即进行维护后飞机发动机的状态会得到改善,但不会恢复到全新状态。通过维护前后状态水平的变化描述这个过程,借鉴Zhu等[25]的思想,对于两个连续衰变的子循环,状态函数关系如式(1)所示
Sk+1(t)=bkSk(t+ekHk)t∈(0,Hk)
(1)
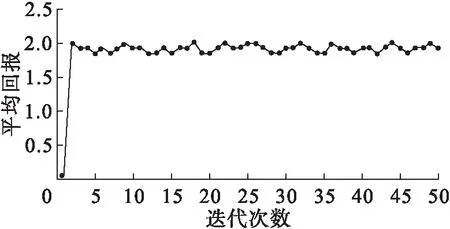
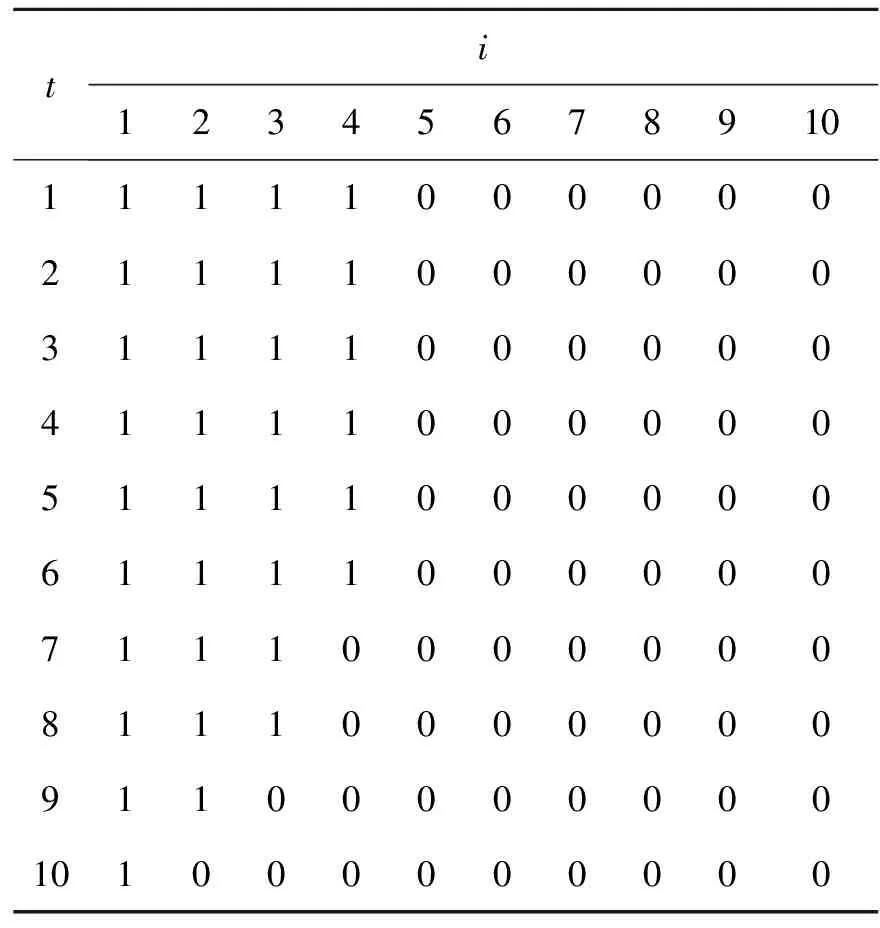
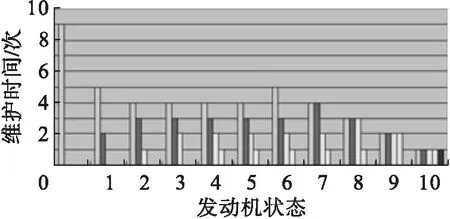
其中:bk为故障率衰减因子,且0 (2) 其中:L是每个子循环k中预先指定的状态水平值,l=1,2,…,L。 针对本文已建立的发动机衰变问题模型,对相关参数在取值区间进行合理取值。飞机发动机进行不完美维护时服从均匀分布U(2,8);大修时间设定为服从伽马分布Γ(20,0.5),当k=1时,其到达维护的时间服从伽马分布Γ(100,0.2)。其他值如表1所示,其中,发动机的状态数n设为10。 表1 参数设定 在强化学习方法中,Q学习方法经常被用于求解类似马尔可夫问题。本文采用策略迭代方式获取最优策略,在最优策略基础上直接获得预测维护时间。当发动机设备处于当前状态s时,采取维护行动a使其转移到状态s′,此时Q值更新为 Q(s,a)=(1-α)Q(s,a)+α[r(s,a,S′)-ρt(s,a,S′)+Q(S′,a)] (3) Q学习算法的流程图如图4所示,详细步骤如下: 图4 学习算法流程图 步骤1.初始化系统值,Q(s,a)=0,k=0,s=(0,0),设置一个较大k值,初始化TOTAL_REWARD,TOTAL_TIME,发动机的状态数n=10。 步骤2.进入系统循环,得到系统的状态s,并计算发动机此时的即时回报和状态转移时间。 步骤3.通过公式(4)~(5)来更新累积的即时收益和状态转移时间 TOTALREWARD←TOTALREWARD+r(s,a,s′) (4) TOTALTIME←TOTALTIME+t(s,a,s′) (5) 更新此时的平均回报率: (6) 更新Q(s,a): Q(s,a)=(1-α)Q(s,a)+α[r(s,a,S′)-ρt(s,a,S′)+Q(S′,a)] (7) 步骤4.通过探索因子β选择行动a,系统状态从s转移到s′,此时系统的即时收益和状态转移时间分别为r(s,a,s′)和t(s,a,s′)。其中,初始化探索因子β为0.5。 步骤5.如果k 步骤6.得到最优维修策略d*: d(l)=argmaxQ(s,a) (8) 通过仿真,可以得到平均回报如图5所示。 图5 平均回报 由图5可见,随着策略更新次数的增加,发动机设备的平均回报率趋于稳定值1.9左右,可以认为这是发动机设备在此模型中学习到的近似最优策略。 s=a(k-iterationtime)b (9) k=20,b=0.1,平均回报:1.942 6 表2中,t表示飞机发动机自上次维护以来的时间,i表示飞机发动机的状态。图6中,横坐标表示飞机发动机自上次维护以来的时间,纵坐标表示下一次的预测维护时间,图中柱形图表示发动机状态的衰变,同一个灰度表示同一个状态。 表2 策略 图6 预测维护时间 由表2可以得出,当飞机发动机当前所处状态i=1、2、3、4、5、6时,飞机发动机距上次维护以来的时间t=1、2、3、4时,飞机发动机不需要进行维护即可继续运行;当自上次维护以来的时间t=5时,就需要开始对飞机发动机进行维护。当飞机发动机当前所处状态i=7、8,飞机发动机距离上次维护以来的时间t=1、2、3时,飞机发动机可以继续运行不需要维护;当自上次维护以来的时间t=4时,就需要对飞机发动机进行维护。当飞机发动机当前所处状态i=9,飞机发动机距离上次维护以来的时间t=1、2时,飞机发动机可以继续运行不需要维护;当自上次维护以来的时间t=3时,就需要开始对飞机发动机进行维护。当飞机发动机当前所处状态i=10,飞机发动机距离上次维护以来的时间t=1时,飞机发动机可以继续运行不需要维护;当自上次维护以来的时间t=2时,就需要对飞机发动机进行维护。 由图6可以得出,当飞机发动机自上次维护以来的时间t=0时,发动机设备处在初始状态,并且预测飞机发动机下一次的维护时间为t=9;当t=1时,最终到达状态2,预测在此状态保持的时间为t=2之后需要维护;当飞机发动机自上次维护以来的时间t=2时,最终到达状态3,预测在此状态运行t=1之后需要进行维护;当飞机发动机自上次维护以来的时间t=3时,最终到达状态3,预测在此状态运行t=2之后需要进行维护;当飞机发动机自上次维护以来的时间t=4,最终达到状态4,并预测在此状态运行t=1之后需要进行维护;当飞机发动机自上次维护以来的时间t=5,最终达到状态4,并预测在此状态运行t=1之后需要进行维护;当飞机发动机自上次维护以来的时间t=6,最终达到状态4,并预测在此状态运行t=1之后需要进行维护;当飞机发动机自上次维护以来的时间t=7,最终达到状态4,并预测在此状态运行t=1之后需要进行维护;当飞机发动机自上次维护以来的时间t=8,最终达到状态4,并预测在此状态运行t=1之后需要进行维护;当飞机发动机自上次维护以来的时间t=9时,最终到达状态4,在此状态运行t=2之后需要进行维护;当飞机发动机自上次维护以来的时间t=10时,最终衰退到状态5,预测此状态下运行t=1后进行维护。由表2结果和图6的预测维护时间可知,当k=20,b=0.25,可得到平均回报为1.866 3。可以发现在此种幂指数情况下,k值保持不变,随着b值的增加,平均回报越来越小。 本文采用了基于强化学习的算法—Q学习算法,通过决策者与动态系统交互过程中所采取的行动进行学习。利用飞机系统监测的数据信息、事件信息、维修信息等作为飞机发动机状态的来源,建立马尔可夫模型,考虑设备维护过程中的预防维护成本、更新维护成本、衰变因子等,通过仿真计算,算出平均奖励来确定最优的维护周期,进而指定合理的维护策略,通过智能算法提高了系统的动态性,延长发动机的寿命,在发动机失效前进行预防性维修或更换,对于解决设备维护问题具有一定的参考意义。3 算例分析
3.1 基本算例参数
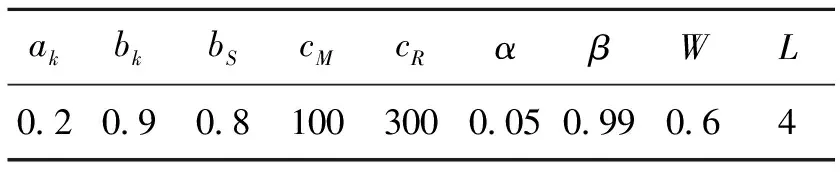
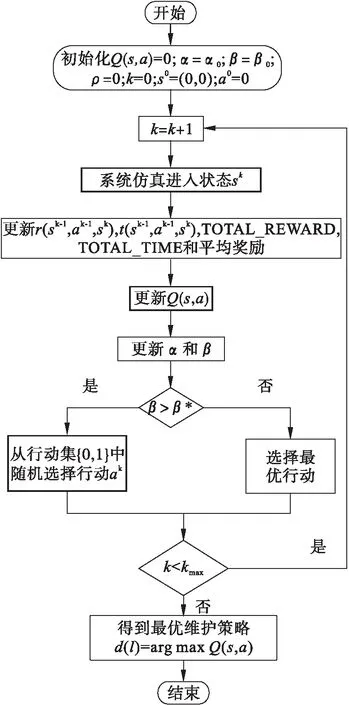
3.2 仿真结果分析
4 结论
