滚装甩挂运输牵引车调度优化及作业模式类比分析

靳志宏，焉红，王小寒，邢磊，徐奇

(1.大连海事大学，交通运输工程学院，辽宁大连116026；2.山东科技大学，交通学院，山东青岛266590；3.桂林电子科技大学，建筑与交通工程学院，广西桂林541004)

0 引言

滚装甩挂运输是由牵引车拖曳带有集装箱的挂车行驶，在滚装船船舱内进行甩挂作业，然后，牵引车下船返回堆场或仓库进行下一个任务。由于滚装甩挂运输模式结合了水路大批量干线运输与陆路支线集疏运的优势，具有广阔的发展前景。2019年2月26日，国家发改委发布《关于推动物流高质量发展促进形成强大国内市场的意见》，大力鼓励和支持甩挂运输等新型运输模式的发展；2019年6月4日，国务院发布《关于加快道路货运行业转型升级促进高质量发展意见的通知》，鼓励挂车共享与接驳甩挂；2020年，交通运输部发布《滚装甩挂操作规程》等4 项标准征求意见函，进一步从政策上给予滚装甩挂足够的支持力度。2020年9月，“中华富强号”船舶成功投入运营(统称为“新船型”)。该船型艏艉开门，大型车辆可直进直出，通行高效。新船型的投入运营，为滚装甩挂码头装卸作业模式的研究提供了技术基础。

与传统运输模式相比，甩挂运输可有效节约牵引车的使用数量、降低运输总成本[1]。XU等[2]在分析甩挂运输的优势和组织方式的基础上，对比研究了全挂车和半挂车的运输效率，得出在运输相同质量的货物时，半挂车的运输效率较高的结论。薛亮等[3]在多点循环甩挂适合不同网络结构形式的运输模式条件下，对牵引车调度优化进行研究。此外，针对交换箱甩挂运输[4]的牵引车调度优化也逐渐成为研究热点。

针对港口甩挂运输，LU 等[5]和常馨玉等[6]分析了港口甩挂运输的特点，指出该模式有助于平衡陆海联运过程中空、重集装箱的运力，降低物流成本，提高多式联运效率。杨珍花等[7]针对空挂任务不确定情形，构建牵引车调度优化数学模型，并设计了模拟退火算法求解模型，同时，用分支定界法求解货滚码头的牵引车调度问题[8]；杨珍花等[9]进一步提出甩挂车辆的动态调度优化问题并开发多阶段动态优化算法求解。SUN 等[10]分析比较ship-swap和port-swap 两种模式，得出在码头牵引车数量不足、任务量大的情况下使用port-swap 模式运行成本更低的结论。

整体来看，由于更高的资源利用率等优势，甩挂运输已引起学者广泛关注并展开研究。但滚装甩挂相关研究相对较少，而不同船型条件下牵引车作业模式与调度优化的研究则尚未涉及。随着船舶大型化、货运量的增加以及船型的改变等现实情况，有必要分析不同船型的牵引车运作情况，确定哪种船型、哪种运作模式的牵引车效率更高。

1 问题描述

本文研究对象包括滚装船、堆场以及有限数量的牵引车。滚装船到港靠泊后，需在规定时间内完成卸货、维修和装船作业。牵引车存放于车场，空、重挂车存放于堆场。以某港调研的数据获取传统滚装船的平面配载图，如图1所示，“BAY”表示贝位，“Sprinkle value”表示消防用的喷淋系统，“AFT”表示船的尾部，“FWD”表示船的前部，“DECK”表示甲板。

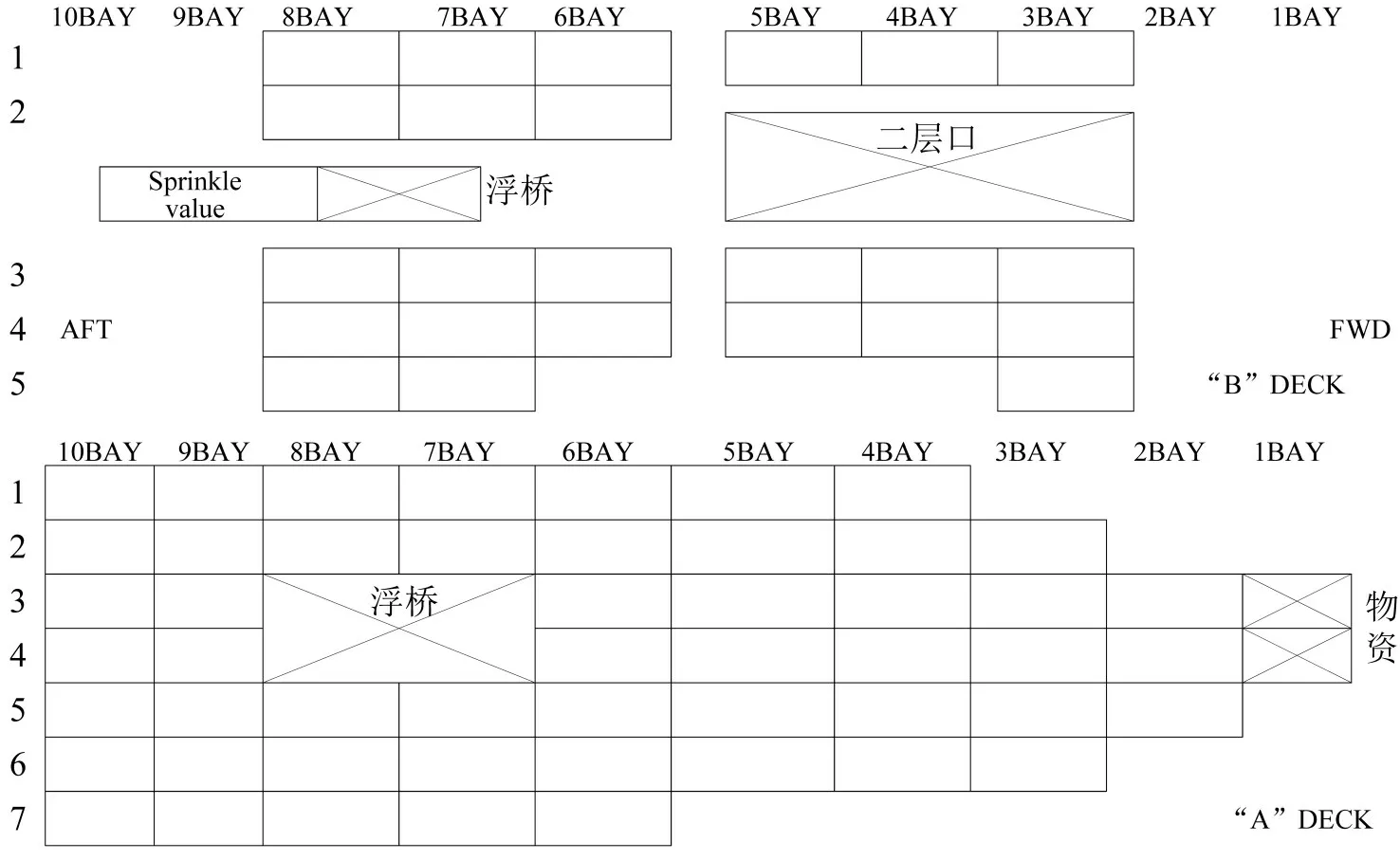
图1 滚装船平面配载图示例Fig.1 Example of plane stowage plan on ro-ro

在滚装船一层(“A”DECK)装载重挂车，二层(“B”DECK)装载集装箱和空挂车。在对滚装船进行装船作业前，先判断货量是否充足以至于是否启用二层。如货量充足，则先装二层(用于装载轻泡货，例如，服装)，再装一层(用于装载重泡货或海鲜类货物)；如货量不足，则将所有货物都装于一层。卸船作业则是先完全卸载一层货物后，再进行二层货物的卸载。

在传统船型条件下，牵引车出入均通过船艉完成(即“船艉进出”)，因此，传统船型装卸船作业只能选择“先卸后装”的作业模式。而在新船型条件下，由于“艏艉开门”，则可以设计“边装边卸”的作业模式进行货物装卸；此时，除艏艉区域需要倒车进行甩挂作业外，车辆在其他区域均可实现“直进直出”。传统船型与新型船型的装/卸任务作业模式如图2所示。

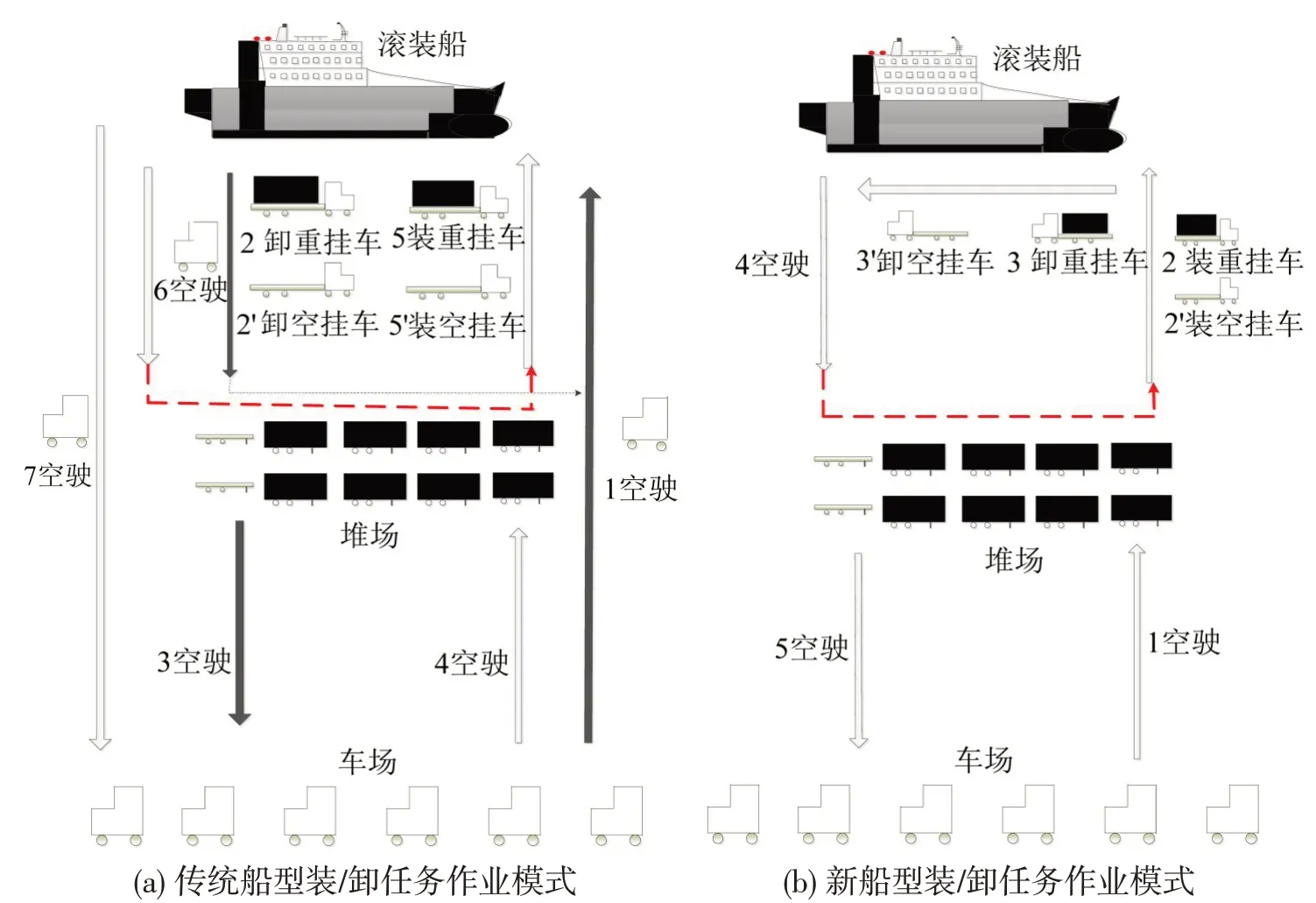
图2 传统船型与新型船型装/卸任务作业模式Fig.2 Loading/unloading task operation mode of traditional and new ship type

图2(a)为传统船型装/卸任务作业模式，灰色箭头指卸船作业模式，牵引车从车场出发，到滚装船挂上重挂车，返回堆场后将重挂车解挂后卸下，连续作业直至任务完成；白色箭头指装船作业模式，牵引车从堆场装载空、重挂车出发，将其卸载至相应贝位，然后返回堆场。所有任务完成后，牵引车返回车场。图2(b)为新船型边装边卸作业模式，牵引车从车场出发到堆场，将空、重挂车装载在滚装船后，再进行卸空、重挂车作业，空驶返回堆场，连续作业直至任务完成，最后返回车场。

本文针对两种船型不同作业模式下，构建以牵引车运营成本最小为目标的数学模型，设计遗传算法求解模型，并进一步分析不同船型的不同作业模式、装卸滚装船任务的最晚完工时间以及系统中装卸船任务位置关系等因素对牵引车运营成本的影响情况。

2 模型构建

2.1 建模假设条件与符号设置

2.1.1 建模假设条件

(1)1辆牵引车只允许拖挂1辆挂车；

(2)牵引车从车场出发，完成分配任务后需要返回车场；

(3)集装箱统一为40尺箱；

(4)不考虑牵引车的转弯角度。

2.1.2 符号设置

(1)参数设置

K——牵引车的数量集合，k∈K；

I——作业任务集合，，其中，I1为装船作业任务，I2为卸船作业任务，0为牵引车从车场到堆场的虚拟任务，0′为牵引车从堆场到车场的虚拟任务；

B——滚装船贝位集合，b∈B；

N——滚装船贝位对应的排集合，n∈N；

P1,i(b,n)——任务i是否属于滚装船下层的第b个贝位的第n列，若是该值为1，否则为0；

P2,i(b,n)——任务i是否属于滚装船上层的第b个贝位的第n列，若是该值为1，否则为0；

l——滚装船上贝位的单位长度；

w——滚装船上贝位的单位宽度；

d1——车场与滚装船之间的距离；

d2——滚装船与堆场之间的距离；

d3——堆场与车场之间的距离；

Di——滚装船上任务i从艉部到贝位之间的距离；

Dij——滚装船上任务i和j之间的距离；

c0——牵引车的固定成本；

c1——牵引车空驶状态下的单位距离成本；

c2——空、重挂状态下牵引车的单位距离成本；

tp——牵引车甩下或挂上挂车的时间；

A1——牵引车在舱外的平均行驶速度；

A2——牵引车在舱内的平均行驶速度；

T——装卸滚装船任务的最晚完工时间；

Y——滚装船的总贝位数；

Z——浮桥所在的贝位。

(2)决策变量

xki——0-1变量，若牵引车k执行任务i，xki=1，否则，xki=0；

ykij——0-1 变量，若连续任务i,j均由牵引车k操作，ykij=1，否则，ykij=0。

(3)状态变量

Ski——牵引车k执行任务i的开始时刻；

tki——牵引车k执行任务i的重载时长；

Fki——牵引车k执行任务i的结束时刻；

Ekij——牵引车k为执行两个连续任务i和j的空驶时长。

2.2 传统船型“先卸后装”调度优化数学模型

传统船型“先卸后装”模式下，先执行完所有卸船任务后，再执行装船任务。因此，该模式下的调度优化模型实际上为卸船调度和装船调度两个数学模型。

(1)传统卸船任务调度优化数学模型

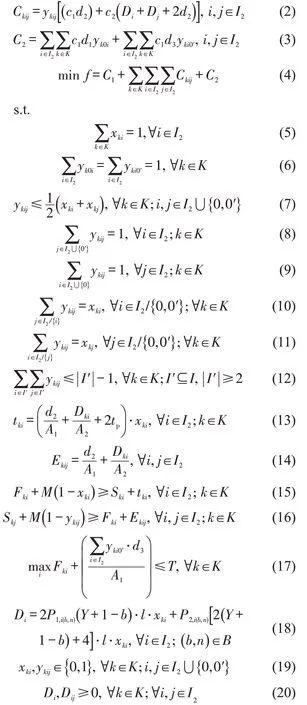
式(4)为传统船型优化模型的目标函数，即最小化牵引车的运营成本，包括：牵引车启用的固定成本，牵引车卸船作业的空、重挂车成本，牵引车的使用成本，分别如式(1)～式(3)所示。式(5)限制每项任务由1 辆牵引车完成。式(6)保证牵引车从车场出发，最终回到车场。式(7)表示两个决策变量xki，xkj与ykij的关系。式(8)和式(9)表示牵引车执行每个任务后只有1个紧后任务。式(10)～式(12)为避免牵引车路径出现子回路的约束。式(13)为牵引车k执行任务i的作业时间。式(14)定义了牵引车卸船作业的空驶时间。式(15)计算了牵引车k执行任务i的结束时间，其中，M表示无穷大。式(16)表示任务i的紧后任务j的开始时间。式(17)表示牵引车执行任务i的完成时刻不能超过系统规定的最晚完工时间。式(18)计算从船艉到牵引车k所执行任务i所在贝位之间的距离。式(19)～式(20)为变量的范围。

(2)传统装船任务调度优化数学模型

传统船型装船任务的约束与卸船任务类似，除式(2)和式(17)外，只需要将卸船模型中任务集合I2全部改为I1。式(2)和式(17)分别替换为

2.3 新船型“边装边卸”调度优化数学模型

新船型的约束与上述传统船型卸船任务的约束在式(1)、式(4)～式(13)和式(16)类似，只需将任务集合I2全部改为I。并将式(2)～式(14)、式(17)和式(18)分别替换为

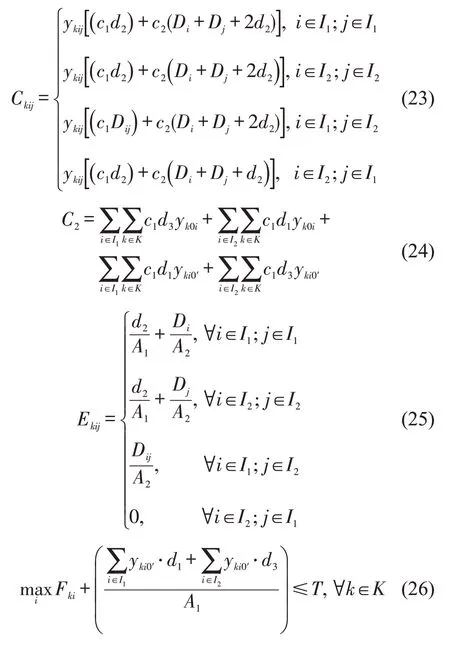
分段函数式(23)表示牵引车不同类型任务(全装、全卸、先装后卸，先卸后装)的空、重挂车成本；式(24)表示牵引车的使用成本；式(25)定义了牵引车不同类型任务(全装、全卸、先装后卸，先卸后装)的空驶时间；式(26)定义了最晚完工时间的范围；式(27)为牵引车k在滚装船上执行任务i和j之间距离的约束。

2.4 模型验证

建立传统船型与新船型的牵引车调度混合整数规划模型，可以利用CPLEX 求解小规模环境下不同任务数。新船型“边装边卸”作业模式的实验结果如表1所示。

表1 “边装边卸”作业模式的CPLEX求解结果Table 1 Solution results of"loading while unloading"mode by CPLEX

由表1 可知，在小规模求解中，随着任务规模的增加，牵引车的运营成本也不断地增加，CPLEX 求解模型的时间也在增加，从而验证了模型的正确性。

3 算法设计

本文研究的牵引车调度优化问题属于NPHard 问题，采用精确算法难以在合适时间内获得最优解。根据问题特点，设计遗传算法求解该问题。算法的流程如图3所示，图中，G表示遗传算法的代数。结合图3，具体的算法核心设计如下：

图3 遗传算法流程图Fig.3 Genetic algorithm flow chart

(1)染色体编码

假设装船任务集合{1,2,3,4,5}，卸船任务集合{6,7,8,9,10}，“边装边卸”作业模式调度的染色体编码规则如图4所示。

图4 染色体编码Fig.4 Chromosome coding

染色体编码是由一个2×10 的矩阵组成，第1行为装、卸船任务编号，先后顺序代表了牵引车的作业顺序；第2行为牵引车编号。例如，图4中灰色阴影部分表示任务4 由牵引车2 进行装船操作，其作业顺序为2。每个染色体的基因长度即为实际任务数。

(2)适应度函数计算

取目标函数的倒数为适应度函数。由于种群中可能出现不满足式(26)的不可行解，即装卸作业完工时间超过最大值，因此，利用惩罚函数法，逐代将其淘汰。适应度函数为

式中：γ为惩罚因子。

(3)交叉算子

在遗传算法的交叉操作过程中，生成[0,1]内随机数，仅当其小于交叉概率时，交叉操作才会发生。为保持个体的可行性，采用顺序交叉算子，如图5所示。

图5 顺序交叉算子示意图Fig.5 Schematic diagram of sequential crossover operator

(4)变异算子

本文所研究问题包括牵引车任务分配和任务排序两个子问题。因此，结合使用交换变异算子与基本变异算子实施变异操作，以保证能够对任务分配与排序进行变异，如图6所示。

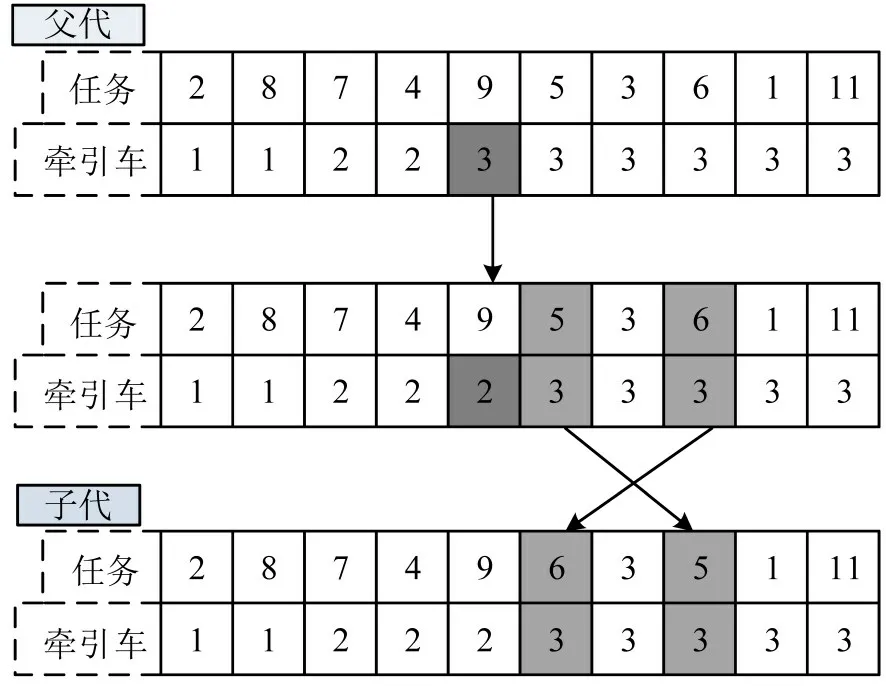
图6 交换与基本变异算子示意图Fig.6 Schematic diagram of exchange and basic mutation operators

4 算例测试与结果分析

4.1 算法有效性测试与结果分析

4.1.1 算法有效性验证

(1)基础数据

以某港的实际数据进行算例分析，牵引车的数量为5辆，算例的基础数据如表2所示。

表2 基础数据Table 2 Basic data

新旧船型的任务设置为20 个装船任务，20 个卸船任务，如表3所示。其中，位置(a,b,c)表示任务位于第a层，b贝位，第c列；状态1、状态-1，表示任务为装、卸船任务。例如，任务1表示装船任务，放在贝位2，第3列。

表3 装/卸船任务在滚装船上的随机位置Table 3 Random position of loading/unloading tasks on ro-ro ship

利用遗传算法求解问题，设定种群规模为100，交叉概率0.90，变异概率0.05，最大迭代次数为500。

(2)遗传算法收敛效果及求解方案

利用Matlab R2016a编写前文所设计的算法程序，运用Windows7操作系统的i7-3770 CPU处理器进行运算。遗传算法求解任务规模为40，新船型模型算例的收敛结果如图7所示。

图7 遗传算法收敛Fig.7 Genetic algorithm convergence

程序迭代500 次后算法终止，共耗时25.97 s，迭代至470 代，目标收敛于996.054 元。可认为算法有效。装卸船任务编号对应执行的牵引车编号及每项任务的作业时间如图8所示。

图8 牵引车完成连续装卸任务的时间分布Fig.8 Time distribution for tractor to complete continuous loading and unloading tasks

(3)遗传算法与CPLEX求解结果对比分析

为验证遗传算法的有效性，将GA与CPLEX的结果进行对比分析，如表4所示。

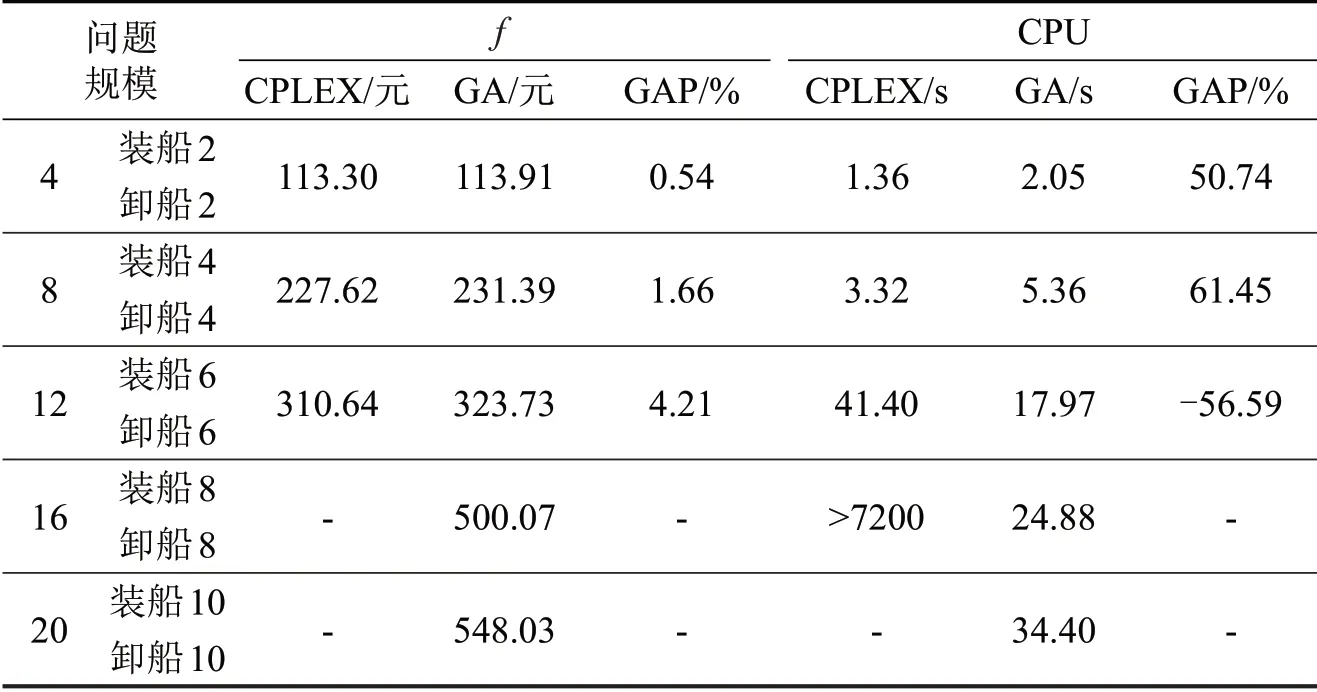
表4 CPLEX与遗传算法实验结果对比Table 4 Comparison of experimental results between CPLEX and GA

当算例规模较小时，GA 求解的目标函数值与CPLEX 精确解比较接近，f的GAP 平均值为1.60%，由此可见，本文所设计遗传算法的有效性。然而，随着任务规模增大，由于避免子回路约束的影响，问题的复杂性也成倍增长，使用CPLEX求解CPU 时长逐渐增大；且当任务规模大于16 时，CPLEX 在有限时间7200 s 无法求解出精确解。而使用本文所设计的遗传算法不仅可获得较优的满意解，且求解时间均在1 min 以内，由此可证明GA算法具备较好的寻优能力。

4.1.2 新船型“边装边卸”和传统船型“先卸后装”作业模式的对比实验

为验证新船型“边装边卸”作业模式的优越性，运用本文设计的遗传算法，比较不同规模下新船型与传统船型不同作业模式的总成本，如图9所示。

由图9 可知，在不同规模下，新船型“边装边卸”作业模式下的总成本均优于传统船型“先卸后装”作业模式下的总成本，且GAP 均大于15%。即“边装边卸”模式可比传统“先卸后装”模式节约成本15%以上。

图9 新船型“边装边卸”模式与传统船型“先卸后装”模式的总成本比较Fig.9 Comparison of total cost between"loading while unloading"mode of new ship type and"unloading before loading"mode of traditional ship type

由图10 可知，在装卸任务数差别极大(例如，1∶7)时，新船型牵引车的运营成本大于传统船型牵引车的运营成本；而当装卸任务数较为接近时，新船型牵引车的运营成本小于传统船型牵引车的运营成本。

图10 “边装边卸”与“先卸后装”作业模式不同任务数比Fig.10 Ratio of different tasks between"loading while unloading"and"unloading before loading"operation modes

4.2 “边装边卸”作业模式的灵敏度分析

4.2.1 装卸任务在滚装船上位置的影响分析

新船型装船与卸船任务在滚装船上的位置，对牵引车在船上行驶的距离有一定的影响，具体情况如表5和图11所示。其中，结合表3，表5中‘-1,1’形式表示卸船任务比装船任务更靠近船艏；‘1,-1’形式表示装船任务比卸船任务更靠近船艏。例如，‘1,-1’形式中的“20交叉”表示20个连续的装船任务紧接20个连续的卸船任务在滚装船的位置分布情况。

表5 交叉方式示意表Table 5 Schematic diagram of crossover mode

由图11 可知，‘-1,1’形式在装卸任务交叉分布密集(10 交叉以前)，且卸船任务越靠近船艏时，牵引车的运营成本越高；在装卸任务交叉分布稀疏(10 交叉以后)，且卸船任务远离船艏时，牵引车的运营成本越高；而‘1,-1’形式则相反，随着装卸任务交叉分布越稀疏，牵引车的运营成本大致呈上升趋势。

图11 装卸任务在滚装船上的位置分析Fig.11 Position analysis of loading and unloading tasks on ro-ro

4.2.2 装卸滚装船任务的最晚完工时间分析

针对不同装卸船任务最晚完工时间条件下的分析，如图12所示。

由图12 可知，“边装边卸”作业模式的运营成本优于“先卸后装”的运营成本。随着最晚完工时间范围的放宽，牵引车的运营成本逐渐降低，在5000～6000 s 时成本降低幅度很大，在9000 s 时，牵引车的使用数量减少至最少。由此看来，新船型“边装边卸”的作业模式受装卸船任务的最晚完工时间的影响，当时间越短，投入的牵引车数量越多才可以保证任务的完成，更有利于码头流转，提高码头运作效率。

图12 装卸船任务的最晚完工时间分析Fig.12 Analysis on the latest completion time of loading&unloading tasks

5 结论

从传统“先卸后装”的作业模式和新船型“边装边卸”的作业模式出发，构建传统装船、卸船以及新船型“边装边卸”模式的牵引车运营成本最小的混合整数规划模型，并根据问题特点，设计遗传算法求解问题。本文得到的主要结论如下：

(1)提出的新船型“边装边卸”作业模式，运用GA 进行求解，得出在不同任务规模下，新船型“边装边卸”作业模式的牵引车运营成本优于传统船型“先卸后装”的牵引车运营成本。

(2)针对新船型“边装边卸”作业模式，通过40个任务规模的算例求解，其装卸任务在滚装船上进行随机分配时，得出“-1,1”形式在装卸任务交叉分布密集，卸船任务越靠近船艏时，牵引车的运营成本越高；在装卸任务交叉分布稀疏，卸船任务远离船艏时，牵引车的运营成本越高；而“1,-1”形式则相反，随着装卸任务交叉分布越稀疏，牵引车的运营成本大致呈上升趋势。

(3)在装卸任务量相同，牵引车数量一定以及装卸滚装船任务的最晚完工时间一样的前提下，相较于传统船型“先卸后装”作业模式来说，新船型“边装边卸”作业模式的牵引车使用数量和牵引车的运营成本整体较低，更有利于提高牵引车的运作效率以及码头的流转。