AGA8方程的积分与应用
2022-03-02张科高欢欢
张科,高欢欢
中国石油大港油田 勘探开发研究院(天津300450)
AGA8-92DC是GB/T 17747.2—2011标准推荐的一个计算工作状态下天然气压缩因子精度较高的方程[1]。在文献[2]中给出了AGA8方程偏导数在天然气物性计算方面的应用。而有些天然气物性参数的计算如定容热容、焦耳-汤姆逊系数、等温焓差、等温熵差等,涉及到状态方程积分的问题[3-5]。在文献[2]基础上,研究了AGA8方程的积分问题,并与其互为补充,进一步拓展和完善了AGA8方程在天然气物性计算方面的应用,对AGA8方程的推广具有重要的工程意义。
1 AGA8积分表达式及理想气体物性
1.1 积分表达式
用AGA8方程计算天然气物性时,其共同特点是都涉及到特定式子的积分,该积分表达式为:
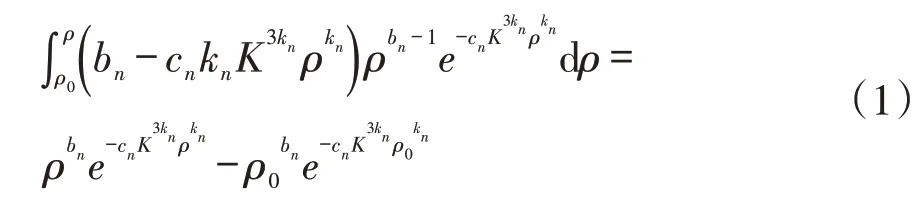
式中:bn、cn、kn为AGA8方程常数,见文献[1]中表B1;K为AGA8方程混合物体积参数,(m3/kmol)1/3;ρ为实际气体混合物摩尔密度,kmol/m3;ρ0为理想气体混合物摩尔密度,kmol/m3。
1.2 理想气体物性
纯物质理想气体的定压热容Cpi0、焓h0i及熵s0i可根据手册中的数据,回归成多项式使用[3]。
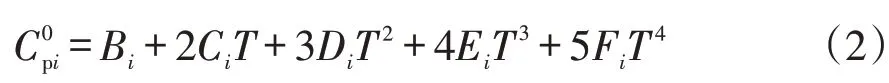

实际气体混合物在低压下的定压、定容比热分别为:

实际气体混合物在低压下的焓、熵分别为:

式中参数单位及意义见表1。

表1 参数单位及意义
2 AGA8方程热容计算
热容计算是天然气物性计算的一个重要方面,气体物性如焦耳汤姆逊系数、过程指数等都离不开气体热容的计算。
实际气体定压、定容热容[4-5]为

式中:Cv为实际气体混合物定容热容,kJ/(kmol·K);p为绝对压力,kPa。
2.1 定容热容计算
从式(6)可知:

根据AGA8方程式推导,并将式(1)、式(10)代入式(9),整理可得:

式中:an、un为AGA8方程常数,见文献[1]中表B1;为AGA8方程中混合物交互作用系数;C*n为AGA8方程中温度和气体组分的函数的系数;Eij为AGA8方程中第二维利系数的二元能量参数;Ki、Kj为AGA8方程中组分i、j的体积参数。
2.2 定压热容计算
得到Cv后,定压热容是通过定压热容与定容热容的关系来计算:定压热容表达式为[2]:

式中:Cp为实际气体混合物定压热容,kJ/(kmol·K)。
2.3 比热比计算

式中:k为气体混合物比热比。
3 AGA8方程焦耳—汤姆逊系数计算
焦耳-汤姆逊系数与偏导数基的关系式为[2],利用计算出的Cp,就得出计算焦耳-汤姆逊系数:
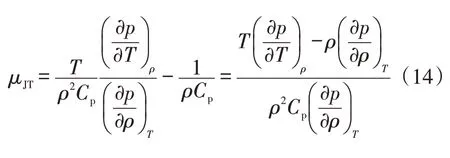
式中:μJT为气体混合物焦耳-汤姆逊系数。
4 AGA8方程绝热指数计算
4.1 温度绝热指数k T计算

温度绝热指数kT的定义[2]为:式中:ZT为气体混合物导数压缩因子。
4.2 容积绝热指数k v计算
容积绝热指数kv的定义[2]为:

式中:kv为气体混合物容积绝热指数;Zp为气体混合物导数压缩因子。
利用文献[6]中ZT、ZP的计算式及文中的CP计算式,即可计算温度绝热指数kT和容积绝热指数kv。
5 AGA8方程等温焓差计算
气体等温焓差有计算式如下[3]:

式中:h为实际气体混合物焓,kJ/kmol;p0=101.325,kPa;v为实际气体混合物体积,m3;v0为理想气体混合物体积,m3。
等温条件下:

式(18)也可用AGA8方程的摩尔密度表示为:


将式(20)、式(22)代入式(18)并整理可得AGA8方程的等温焓差计算式:

6 AGA8方程等温熵差计算
气体等温熵差表达式为[3]:

根据AGA8方程,推导可得:
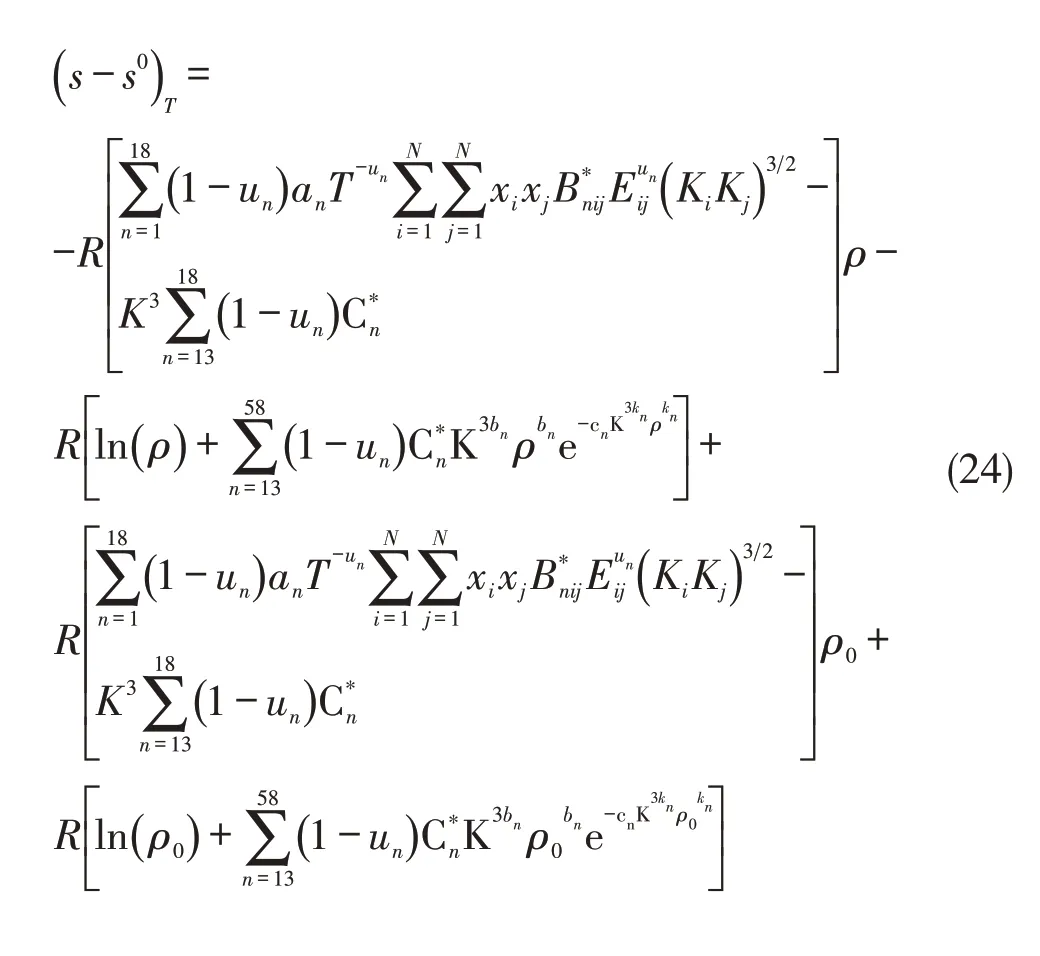
7 AGA8在天然气物性计算中的应用
7.1 用AGA8方程计算温度绝热指数
温度绝热指数在天然气物性计算及工程热力学计算中都是一个重要参数,本文采用上述方法,选取了文献[6]中的部分工况条件对温度绝热指数进行了计算,计算结果见表2。
从计算结果看,用AGA8方程计算天然气的温度绝热指数是可行的,表2中计算最大误差都不超过2%,由此可见,该方法可以应用到工程实际中。
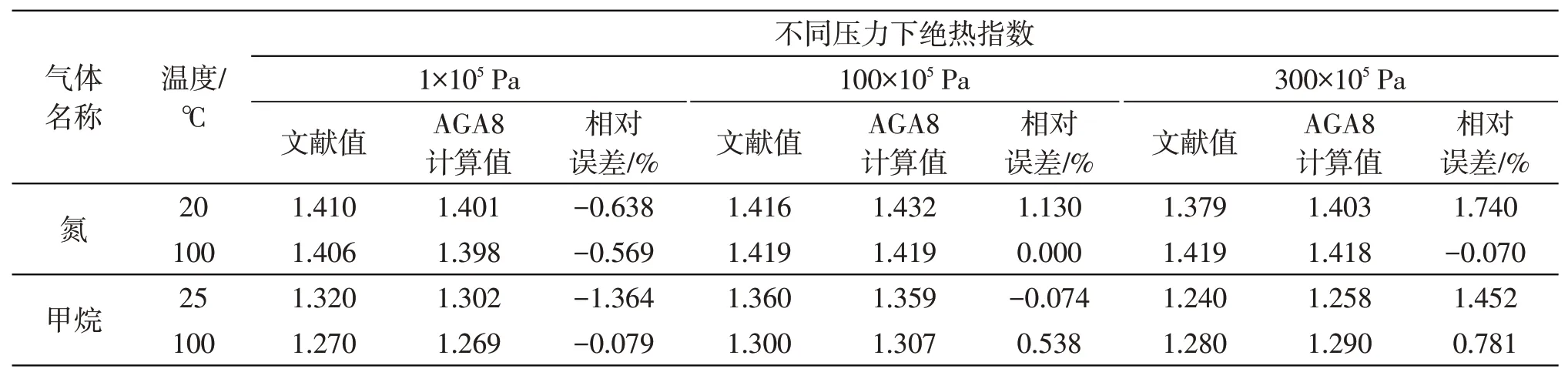
表2 气体的温度绝热指数K T
7.2 用AGA8方程计算天然气的其他物性参数
GB/T 17747.2—2011标准的附录C中给出6组不同组分的天然气气样,每组气样给出了2种压力和5种温度输配条件下的Z值。为便于比较,本文按文献[2]的方式对前3种气样只选取了一种输配条件,用AGA8方程和BWRS方程进行了对比计算。
表3标准中Z值是GB/T 17747.2—2011标准给出的数值,表中其他数值是扩展计算结果。

表3 1#、2#、3#气样物性计算比较
从上述计算可以看出:采用AGA8-92DC方程计算定压热容、定容热容、焦耳汤姆逊系数、比热比、焓差、熵差等天然气物性是可行的。从与BWRS方程的计算对比可以看出,计算结果可信。
8 结束语
通过对AGA8方程的积分研究,给出了天然气的定压热容、定容热容、焦耳-汤姆逊系数、焓、熵、温度绝热指数、容积绝热指数等多种天然气物性计算的数学表达式,建立起了AGA8方程在天然气物性计算方面较为完整的数学模型体系,进一步拓展和完善了该方程的应用范围,对GB/T 17747.2—2011推广和应用有进一步的提升。该方法的计算误差不超过2%,可应用到实际工程计算中。
