鼓形齿联轴器的曲率系数计算研究

2022-03-02卢茜莉陈云峰吴世祥杨远航

重型机械 2022年1期

卢茜莉，陈云峰，吴世祥，杨远航

(泰尔重工股份有限公司，安徽马鞍山 243000)

0 前言

鼓形齿联轴器是一种刚性可移式联轴器，是机械传动的重要基础部件。鼓形齿联轴器能够补偿两轴间径向、轴向、角度以及综合位移，具有承载能力高、传递转矩范围大、耐久性好、许用转速高等优点。鼓形齿联轴器广泛应用于冶金、采矿、化工、船舶、起重运输等各种机械设备中[1]。在鼓形齿联轴器的设计和生产中，曲率系数是一个非常重要的几何尺寸参数，不仅直接决定鼓形齿的几何尺寸，而且与鼓形齿联轴器的承载能力、轴间倾角、齿侧间隙等息息相关。目前在鼓形齿联轴器的相关设计中，其几何尺寸参数大都凭借经验和引用相关手册决定[2]，缺乏理论支撑；虽然部分文献[3、5、8]对曲率系数的计算也有了相关研究，但研究不够深入，理论依据不够完善，计算公式也不够全面，对鼓形齿几何尺寸设计不具有普遍的指导意义。本文提供一种比较完整的鼓形齿联轴器曲率系数的理论计算，并总结出各参数对曲率系数的影响规律，为进一步对鼓形齿联轴器的研究提供参考。

1 位移圆半径和曲率半径

鼓形齿联轴器在工作中，在两轴线之间要允许一定的倾角。所以，在鼓形齿的设计中，保证齿轮在最大倾斜的条件下，不发生内齿与外齿边缘接触，不产生端部载荷。因此，加工鼓形齿时，刀具是按半径为R的圆弧移进的。

鼓形齿可用插齿和滚齿两种方法进行加工，用插齿法加工出的鼓形齿，齿廓渐开线始终垂直于鼓形齿轴线。如图1a所示，进而可计算出离中心x处，垂直于轴线方向上的刀具移进量Yc。

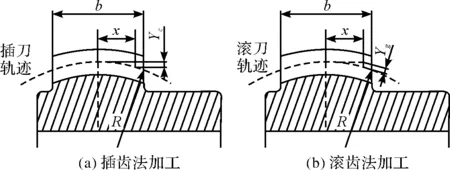
图1 刀具轨迹示意图

(R-Yc)2+x2=R2

(1)

(2)

用滚齿法加工出的鼓形齿，齿廓渐开线始终垂直于位移圆。如图1b所示，进而可计算出离中心x处，垂直于位移圆的刀具移进量Yg。

R2+x2=(R+Yg)2

(3)

(4)

式中，R为位移圆半径；Yc为插齿刀具移进量；Yg为滚齿刀具移进量；x为离齿宽中截面处的距离。

如图2所示，在鼓形齿中间截面中，A-A面为工作圆切面，过啮合点与工作圆相切；B-B面为齿啮合平面。

图2 鼓形齿的曲率半径

通过计算可知，鼓形齿廓在A-A、B-B截面中为椭圆或者双曲线，各点的曲率半径不同，计算时可将齿廓曲线看成圆弧近似计算，则鼓形齿齿宽与曲率半径的关系为

b=2rtsinωt

(5)

b=2resinωe

(6)

式中，b为鼓形齿齿宽；rt为工作圆切面内的曲率半径；re为齿啮合平面内的曲率半径；ωt为工作圆切面内的最大允许倾角；ωe为齿啮合平面内的最大允许倾角。

在截面A-A、B-B内，离齿宽中截面x处分别有单边的齿厚差yt、ye，也称为单侧减薄量。单侧减薄量与刀具移进量之间的关系如图3所示。

图3 鼓形齿单侧减薄量

在图3中，圆心到啮合点射线方向与中心线的夹角称为加工角。在极小的范围内，可将齿廓曲线近似看成一条直线，则单侧减薄量为

ye=Ysinα*

(7)

yt=Ysinα*/cosαw

(8)

式中，Y为插齿或滚齿刀具移近量；yt为工作圆切面内的单侧减薄量；ye为齿啮合平面内内的单侧减薄量；θ为加工角(θ=90°/Z，Z为齿数)；α为压力角；α*=α+θ；αw=α-θ。

以计算啮合平面内的单侧减薄量为例，将式(7)分别代入式(2)和式(4)中，得

(1)插齿法。

(9)

进一步变换

(10)

(2)滚齿法。

(11)

进一步得

(12)

公式(10)和(12)分别为椭圆方程和双曲线方程，由此可知，插齿法加工出来的鼓形齿齿廓曲线为椭圆，滚齿法加工出来的鼓形齿在啮合平面内齿廓曲线为双曲线。同理，在工作圆切面内齿廓曲线也是椭圆或双曲线。

2 工作倾角和齿的圆周位置问题

鼓形齿最大的特点就是在轴心线上允许一定的工作倾角来实现补偿位移。当鼓形齿倾斜一定角度时，不同圆周位置的齿在啮合平面或工作圆切面上的倾斜变化量是不一样的，所以，需要考虑哪个位置的齿最大允许倾角最小，即找到最容易发生端部载荷的齿来进行计算。以插齿法为例，计算在齿啮合平面内鼓形齿倾斜一定角度时，各参数之间的关系。

当渐开线直齿轮的轴心线在倾斜一定角度ω后，在齿廓节圆线上的任意一点M在啮合平面内到倾斜之前节圆线上的垂直距离称为直齿轮的间隙变化量Δ直，如图4a所示。

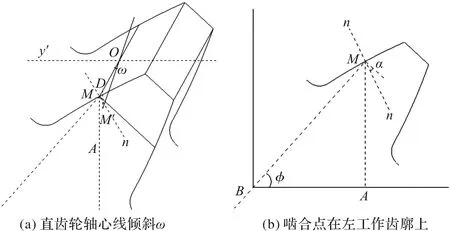
图4 倾斜直齿轮

Δ直等于DM′在齿廓法线n上的投影，即

Δ直=DM′cos∠nMA

(13)

在位于任意圆周位置φ的齿上，假设啮合点在左工作齿廓上，如图4b所示，则

φ=∠nMA+α

(14)

∠nMA=φ-α

(15)

当啮合点在右工作齿廓上，同理可得

∠nMA=π-(φ+α)

(16)

即

Δ直=|DM′cos(φ±α)|

(17)

设齿廓节圆线上的任意一点M到中心点O的距离MO为x，则

DM′=xsinω

(18)

Δ直=|xsinωcos(φ±α)|

(19)

当鼓形齿的轴心线在倾斜一定角度ω后，其间隙变化量Δ就等于直齿间隙变化量Δ直加上齿啮合平面内的单侧减薄量ye，即

Δ=Δ直+ye

(20)

将式(2)和式(7)代入式(20)，得

Δ=|xsinωcos(φ±α)|+

(21)

式中，ω为鼓形齿轴心线的倾斜角度；Δ为在啮合平面内鼓形齿倾斜后的间隙变化量；Δ直为直齿倾斜后的间隙变化量；φ为齿的任意圆周位置。

由于鼓形齿联轴器的内齿一般都为直齿，当鼓形齿与内齿刚好不发生齿端载荷时，即鼓形齿与内齿相切，所以以x为自变量，对Δ进行求导，当导数为零时刚好是临界状态。

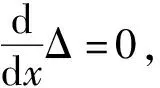
(22)

位于不同圆周位置的鼓形齿，其与内齿的切点位置也不相同，为了不产生端部载荷，鼓形齿的齿宽b必须要大于等于两倍的|x|的极大值。

当φ=±α或π±α时，x取极大值，即位于这四个圆周位置的齿最容易发生端部载荷。

(23)

则可看成

(24)

3 曲率系数的计算

曲率系数等于曲率半径与位移圆半径的比值，计算插齿法加工的鼓形齿在齿啮合平面内的曲率系数ψce。将式(6)代入式(24)中，得

(25)

当φ=±α或π±α时，这四个圆周位置的齿的轴心线倾斜方向刚好是在齿啮合平面内，所以有

ω=ωe

(26)

即

(27)

其中，ψce为插齿法齿啮合平面内的曲率系数。

当计算工作圆切面的曲率系数时，将式(8)代入计算，同理求出鼓形齿倾斜ω角度后的间隙变化量Δ′。

Δ′=|xsinωcos(φ±α)|+

(28)

(29)

从而可得

(30)

其中，ψct为插齿法工作圆切面内的曲率系数。

以鼓形齿联轴器参数(ω=0,α=20°)为例，计算不同齿数时的工作圆切面内的曲率系数ψct和齿啮合平面内的曲率系数ψce。工作圆切面内的曲率系数ψct和齿啮合平面内的曲率系数ψce都随着齿数Z的增大而增大。如表1所示，对比《齿轮手册》的曲率系数，本文工作圆切面内的曲率系数ψct的计算结果误差在0.02左右，齿啮合平面内的曲率系数ψce的计算结果误差在0.01左右。由此可证明本文的计算方法是正确的。