基于树冠生长和空间竞争指数的油松风景林经营密度表编制
2022-03-02孙广鹏章志都刘海轩朱济友徐程扬
孙广鹏,章志都,刘海轩,朱济友,徐程扬
(1.北京林业大学,北京 100083;2.福建省三明市林业局,福建 三明 365000;3.清华大学,北京 100084)
林分密度是林分生长的重要指标,是人工林经营中最重要的可控因素之一[1]。而对于风景林,林分密度不仅与林分产量和质量有关[2-3],还通过影响林木树冠生长[4]、林下植物多样性[5-6]、林分通透度和林内可及度[7]等影响景观质量。此外,林分密度过大会导致林木个体间的竞争加剧进而引起窄冠、偏冠、被压木等问题,还会影响林分中幼苗、幼树的生长发育[8],这些对风景林美学质量都有着不容忽视的作用。一是因为窄冠、偏冠、被压木等会制约林分中大树的出现,而大树恰好在提高林分美学质量中有极为重要的作用[4]。二是幼苗、幼树不仅能通过填充林分垂直空间对林分美学质量产生影响,甚至因为未来可能成为林分景观的基调个体而对林分美学质量有潜在贡献。
林分密度管理主要依据林分经营密度表(图)和林分可收获模型。传统的编制方法主要有“林分密度—胸径—冠幅”法[9]、最大密度线法[10]、疏密度法[11]等,以优势高和林分密度为自变量、以单株平均材积、平均胸径以及单位面积蓄积量为因变量构建非线性回归[12]或单木结构生长方程[13],这些方法忽略了竞争对林木个体生长的影响[14]。近期林分密度管理的研究中,学者们建立了关于胸径[15]、胸高断面积[16]、树高[17]、蓄积量[18]等的生长模型,基于贝叶斯法对林分最大密度线进行研究[19],探究合理的林分密度。虽然部分模型构建时,已经考虑了林分竞争对单木生长的影响,但只是从杉木[20]、红松[21]、落叶松[22]等用材树种的材积出发,关注点仍局限于胸径、树高、断面积等生长指标,而树木之间的竞争更多出现在树冠相互重叠或根系发生接触时[23]。而要科学合理地调整风景林密度,首先要了解风景林树种树冠生长的特点。因此,本研究以油松人工风景林为例,在综合考虑林分密度与林木个体间竞争关系的基础上,通过生长量修正法构建油松单木树冠半径生长模型,并基于树冠面积控制法,针对不同立地条件、不同林分年龄、不同竞争强度建立风景林经营密度表。
1 试验地概况
研究区位于北京市西山试验林场,地处低海拔山区,平均海拔300~400 m,最高800 m,平均坡度为15~35°,土壤主要类型为山地褐土。气候为典型的暖温带半湿润季风大陆性气候,年平均气温10~12℃,年平均降水量600 mm。林场总面积5 910 hm2,其中林业用地5 892 hm2,森林覆盖率为98.2%。林场内天然林较少,绝大部分为人工林,以油松Pinus tabulaeformis、侧柏Platycladus orientalis、栓皮栎Quercus variabilis、刺槐Robinia pseudoacia、黄栌Cotinus coggygria、山桃Amygdalus davidiana等为主。
2 研究方法
2.1 林分调查
参考章志都[24]的方法,采用典型抽样的方法设置61 个20 m×30 m 的标准样地,调查每块样地的林分年龄、林分密度,用全站仪(NTS—662)测量每株单木的相对坐标。通过每木检尺进行林分结构调查,记录每株树的种名、胸径、树高、冠幅(四个方向)、枝下高。其中,用围尺测量胸径,以2 cm 为起测径阶,精确到0.1 cm;用勃鲁莱测高器和测高标杆测量树高和枝下高,精确到0.1 m;用皮尺测量4 个方向的冠幅,精确到0.1 m;根据林木生长状况确定各标准地内的优势木和平均木,并分别筛选出树冠结构相对完整的优势木和平均木各1 株作为采集枝条的样木,用于分析油松林木树冠半径生长规律。记录枝条在树干上的高度、枝角和枝长,用于计算树冠半径。
为了便于差异性统计分析,将样地分为4个密度等级:密度等级Ⅰ(简写为Class1),林分密度<600株/hm2;密度等级Ⅱ(简写为Class2),林分密度为600~1 000 株/hm2;密度等级Ⅲ(简写为Class3),林分密度为1 000~1 400 株/hm2;密度等级Ⅳ(简写为Class4),林分密度>1 400 株/hm2(表1)。

表1 样地信息概况Table 1 Information summary for the investigated plots
2.2 邻体竞争木选择
采用Voronoi图来确定对象木的竞争木。参考汤孟平等[25]的方法,采用ArcGIS 软件生成Voronoi多边形来确定邻体竞争木。为消除边缘影响,使用“8 邻域法”样地进行边缘校正,即在样地的上、下、左、右、左上、左下、右上、右下8个邻域复制原样地,形成9 个样地组成的大样地。计算竞争指数时,对象木仅包含原样地内的树木,即图1 实线框内的林木。

图1 边缘矫正和树木竞争Voronoi 图Fig.1 Marginal correction and Voronoidiagram of tree competition
2.3 单木竞争指数的构建
树冠特征与树冠间的竞争对风景林景观质量具有重要影响,本研究在传统单木竞争指数的基础上引进树冠变量(冠幅、冠长、树冠表面积和树冠体积)构建相应的竞争指数,构建的竞争指数主要分为与距离无关的竞争指数和与距离有关的竞争指数。
2.3.1 与距离无关的单木竞争指数的构建
与距离无关的竞争指数常采用胸径、树高及其相对比值来构建。竞争指数中引进树冠变量可以提高竞争测度的性能[26],因此,本研究引用树冠因子构建了与距离无关的树冠竞争指数,相对胸径RD、相对树高RH、相对冠幅RCW、相对冠长RCL、相对树冠表面积RCS、相对树冠体积RCV,分别用以下公式表示:
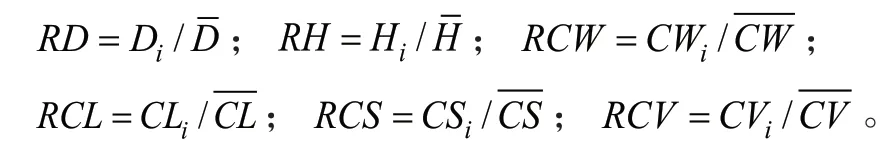
式中:Di、Hi、CWi、CLi、CSi、CVi分别为第i株树的胸径、树高、冠幅、冠长、树冠表面积和树冠体积;分别为林分平均胸径、平均树高、平均冠幅、平均冠长、平均树冠表面积和平均树冠体积。
2.3.2 与距离有关的竞争指数的构建
与距离有关的单木竞争指数中常采用在某一量纲下对象木和竞争木的大小以及它们之间的距离作为变量,单木竞争指数取决于所选择的变量以及用来定义相邻木作为竞争木方法之间的函数关系。
与胸径有关竞争指数CID:
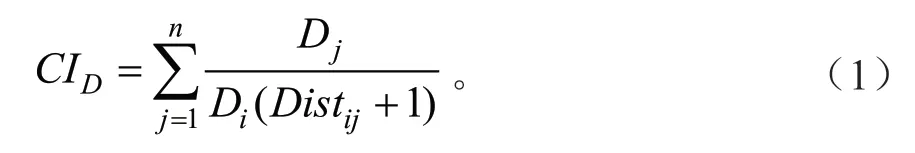
与树冠表面积有关竞争指数CICW:
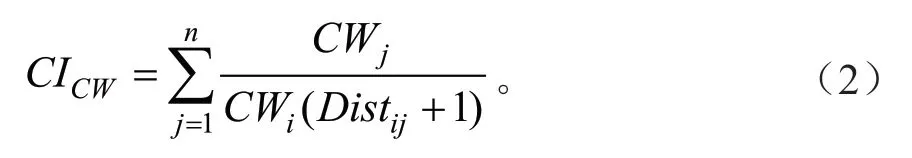
与树冠表面积有关竞争指数CICS:
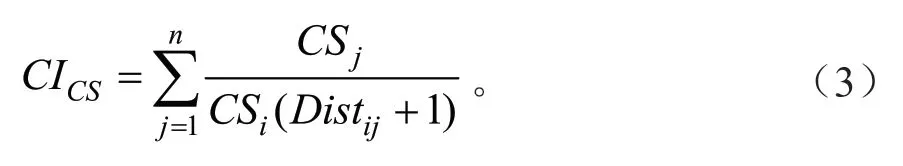
与树冠体积有关竞争指数CICV:
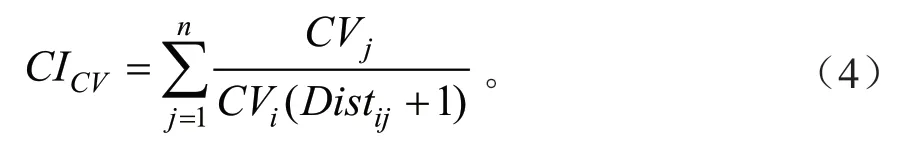
式中:Distij为第i株对象木到第j株竞争木之间距离;Di、CWi、CSi、CVi分别为第i株对象木的胸径、冠幅、树冠表面积和树冠体积;Dj、CWj、CSAj、CVj分别为第j株竞争木的胸径、冠幅、树冠表面积和树冠体积。
2.4 竞争指数的筛选
以冠幅为因变量,基于2.3 中竞争指数构建了生长竞争模型(公式5),用树冠生长数据对模型进行拟合,对待估参数进行估计,并在对各个指数灵敏性进行比较的基础上确定最适当的竞争指数。
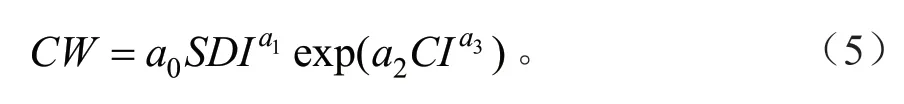
式中:CW为冠幅,SDI为林分密度指数,CI为竞争指数,a0、a1、a2、a3为待估参数。

式中:N为现实林分每公顷株数;D0为标准平均直径(D0=20 cm);D为现实林分平均直径;b为完满立木度林分的株树和平均直径之间的方程的斜率,油松林b值为-1.528 6[27]。
2.5 单木潜在树冠半径生长模型
将样地按密度分级,按比例选取90%(52 块)的样地数据,采用生长量修正法[32]建立单木树冠生长模型。首先选用Richard 方程(公式7),参数A与树冠半径的最大值呈正相关[28],冠幅半径与树木胸径成正比,参数k随树高增大而增大,因此构建拟合油松单木潜在树冠半径生长的基础模型(公式8):
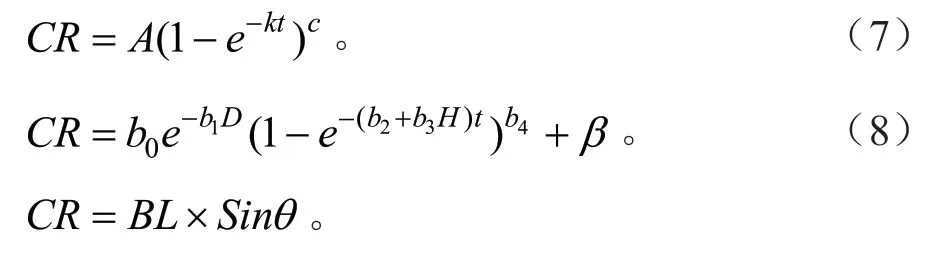
式中:CR为树冠半径,b1、b2、b3、b4为未知参数,H是树高,D是树木胸径,θ是枝角,即一级枝与树干的夹角。
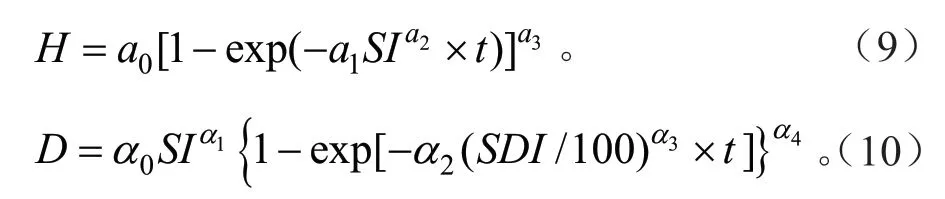
式中:H是标准木的平均高;D是标准木胸径;SI是立地指数[27];t是树木年龄;a0、a1、a2、a3;α0、α1、α2、α3、α4是模型参数。
2.6 单木树冠半径生长模型的建立
参考刘兆刚等[26]的模型修正法将SDI与RCS及其变量变化形式作为修正变量进行拟合筛选和函数构造修正,对潜在树冠半径生长模型进行修正,得到可用于实际生产的油松风景林单木树冠半径生长模型。
2.7 模型参数估计及有效性检验
用DPS 软件对树冠半径生长模型进行非线性参数估计。根据残差平方和(RSS)、估计标准误差和决定系数来评定方程拟合的优度,对模型参数进行筛选。利用未参与模型模拟的10%的独立样本计算平均偏差、平均绝对偏差、平均相对偏差、平均相对偏差绝对值和预测精度,对模型进行有效性检验,具体计算方法见文献[24]。
3 结果与分析
3.1 单木竞争指数筛选
变异性分析结果(表2)表明,不同林分密度等级RCS、CICS、CICV3 个竞争指数的变异系数相对较大,说明这几个竞争指数对林分密度变化的反应比较灵敏,对林木间竞争具有较强的解释能力。竞争模型模型参数估计结果(表3)表明,采用RCS、CICS、CICV构建的竞争模型的F检验虽然均达到显著性水平(P<0.01),然而用RCS拟合竞争模型时决定系数最大(R2=0.650 6,P=0.000 1)、剩余标准差最小,表明RCS最适合作为竞争指数拟合油松树冠的生长。
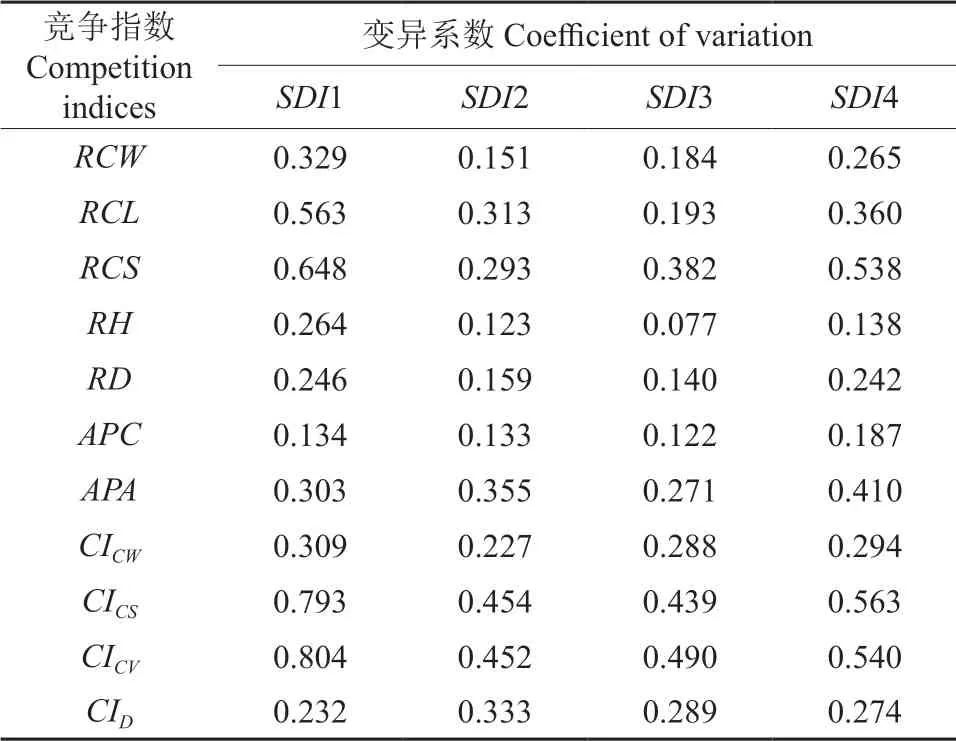
表2 不同林分密度油松各种竞争指数的变异系数Table 2 Coefficient of variation(COV)of competition indices of planted Pinus tabulaeformis forests with different stand densities

表3 油松单木竞争模型参数估计结果Table 3 Parameter estimation results of single tree competition model of Pinus tabulaeformis
3.2 油松人工风景林单木潜在树冠半径生长函数
单木潜在树冠半径生长模型的参数估计检验结果如表4所示,模型各个参数的F检验结果均达到极显著水平(P<0.01),R2值为0.930 5,说明模型拟合效果好,能用于模拟油松单木潜在树冠半径生长规律。
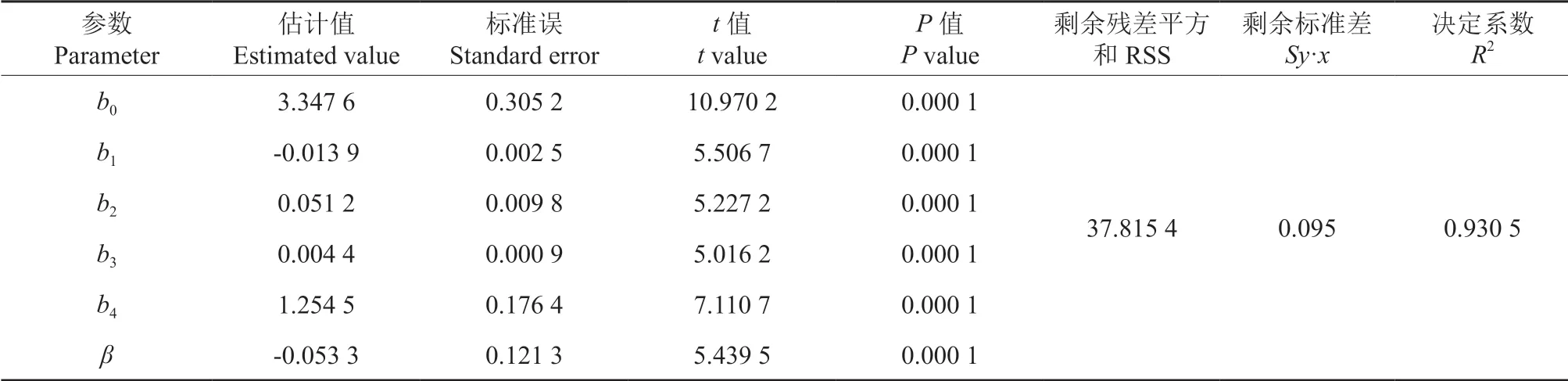
表4 油松潜在树冠半径生长模型参数估计结果与拟合统计量Table 4 Parameter estimates and fitting statistics of the potential canopy radius growth model of Pinus tabulaeformis plantations
3.3 修正后树冠半径模型拟合与参数检验
基于林分密度和林分竞争指数修正后的单木树冠半径生长模型如公式(11)所示:
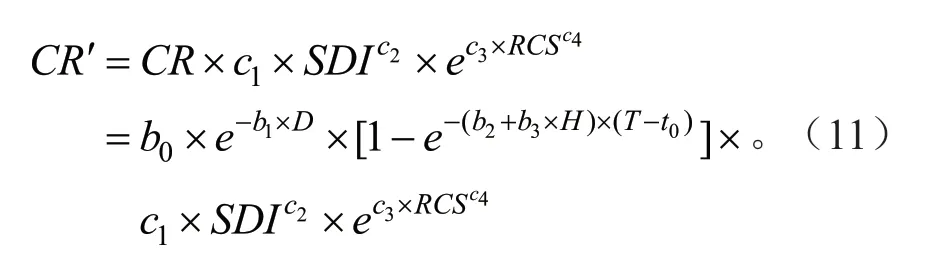
式中:CR′为林分中树木的树冠半径;T为树木年龄,c1、c2、c3、c4为待定参数;t0为树木生长到取枝高度时的年龄,根据公式和a3通过树高生长模型进行拟合分析确定(表5)。由模型参数估计和拟合统计量结果(表6)可以看出,模型各参数的F检验值均达到极显著水平(P<0.01),且决定系数达到0.843 6,说明引入林分密度指数和空间竞争指数为修正函数的油松单木树冠半径生长模型拟合效果较好。

表5 油松树高生长模型参数估计结果与拟合统计量Table 5 Parameter estimates and fitting statistics of the height growth model of Pinus tabulaeformisplantations

表6 油松单木树冠半径生长模型参数估计结果与拟合统计量Table 6 Parameter estimates and fitting statistics of the canopy radius growth model of Pinus tabulaeformisplantations
3.4 模型预测能力检验
树冠半径生长模型预测结果(表7)与实测值之间平均误差最大值为-0.53,绝对标准误差的最大值为0.57,潜在树冠半径的预估精度为94.53%,单木树冠半径的预估精度为89.03%。经检验,模型预估精度大于85%,能够有效地预测林分树冠半径的生长。

表7 预测模型检验结果Table 7 Test results of the growth estimation models
3.5 油松人工风景林经营密度表编制
基于修正后的树冠半径生长模型和段劼等[29]编制的油松人工林立地指数表,建立了不同立地指数不同竞争条件下的“树冠半径—林分密度”经营密度表。从油松人工林经营密度表(表8)可以看出,相同立地条件和龄级的林分中,竞争指数越大,其竞争强度越低,相应的树冠半径越大,林分密度越小。按照章志都[24]林内景观要素特征的分析结果将风景林划分为封闭型中、高密度纯林、观赏型中密度纯林、开放休闲型低密度纯林3 种经营类型,对应竞争指数分别为0.8~0.9、1.0~1.1、大于1.2。随着林分生长,树冠半径逐渐增大,因此在森林经营过程中应根据培育目标适当地调整林分密度维持相应的竞争强度。以地位指数为4的油松风景林为例(表8),10 龄级时无竞争的优势木的单木树冠半径为1.5 m,适宜的林分密度应为1 509 株/hm2;15 龄级的优势木树冠半径为2.0 m,为了维持无竞争状态,林分密度应调整为775 株/hm2。而如果培育目标是封闭式观赏林,应控制竞争指数为0.8~0.9,10 龄级平均树冠半径为1.0~1.1 m,适宜的林分密度为2 664~2 986 株/hm2;15 龄级的树冠半径为1.4~1.5 m,适宜密度为1 434~1 607 株/hm2。
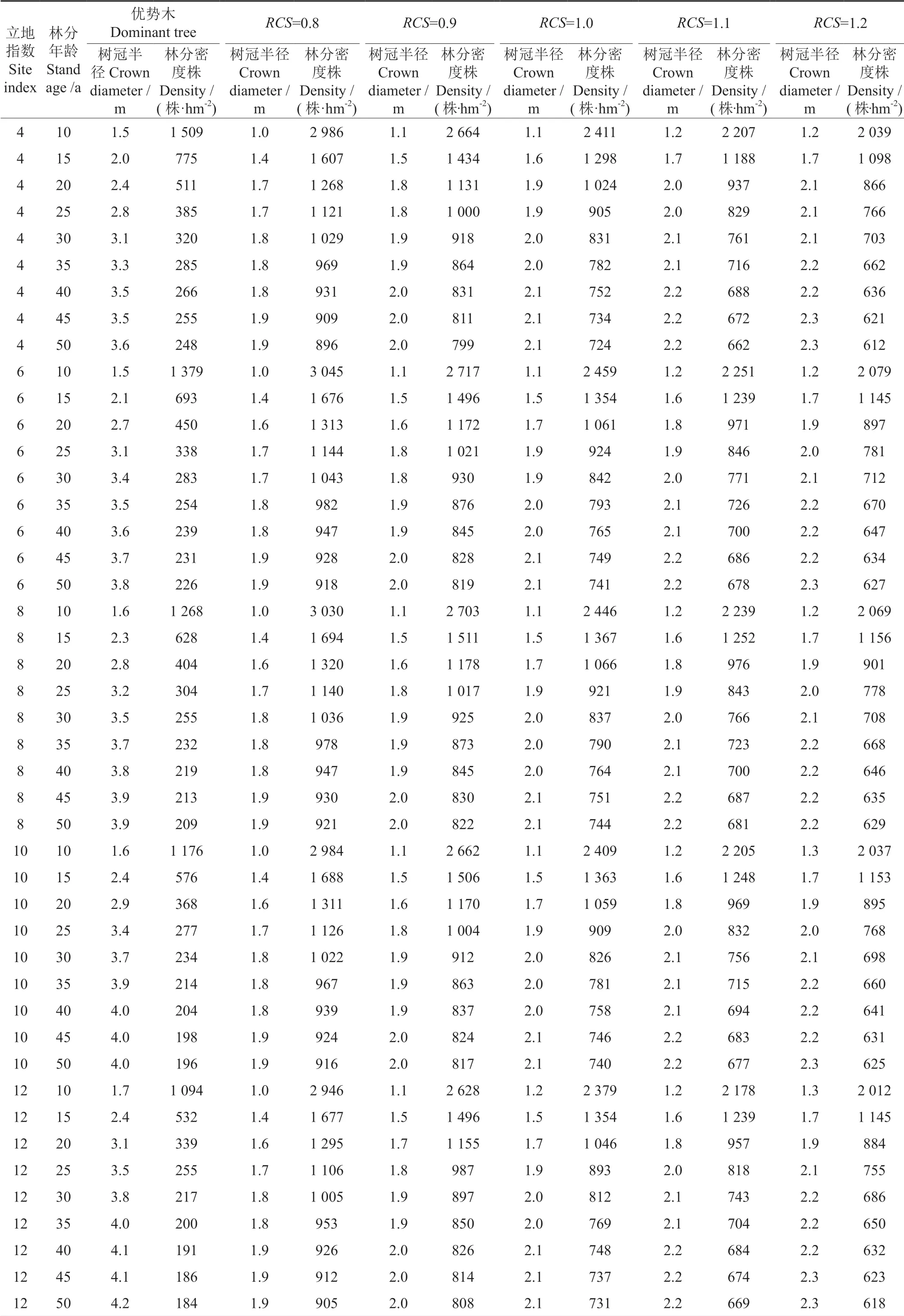
表8 不同立地条件、不同竞争强度油松人工林经营密度表†Table 8 Management density table of Pinus tabulaeformis trees in different sites with different competition intensities
4 讨论
通过Voronoi图确定对象木的邻体竞争木,不仅有效地避免了传统半径圆取样法中因尺度不统一导致研究结果缺乏可比性[30-31]和因树木个体生长差异导致的错选、漏选竞争木的问题[25],还充分考虑了每个树木个体的空间占有度,得到了更大的树冠半径和更小的林分密度,更贴合风景林经营的实际情况。指数研究在构建竞争指数时引入了相对树冠表面积,而树冠表面积代表了林分的有效光合面积,更好地反映了林木个体间营养利用和能量获取的竞争。在生长竞争模型的研究中,竞争指数主要分为与距离有关的竞争指数[32]和与距离无关的竞争指数两大类[33],其中与距离有关的竞争指数相对精确,结果更为可靠,但是操作和计算更为复杂。而本研究引入树冠变量建立的与距离无关的竞争指数,在操作简单的同时也能提高对竞争压力表征的精度[26],能够有效减少操作步骤,提高竞争指数的测算效率。风景林经营中,树冠变量对林分景观质量有着重要影响[34]。以单木树冠半径作为指标研究林分密度对林分竞争和单木生长动态的影响,发现随着林分密度的增大,竞争压力也在逐渐增大,平均树冠半径逐渐减小。根据章志都[24]对林内景观要素特征的差异性分析结果,将调查林分按照林分密度1 100~1 800、725~1 266 和425~557 株/hm2划分为3 种类型,结合林下通视距离特点将风景林划分为封闭型中、高密度纯林、观赏型中密度纯林、开放休闲型低密度纯林,其对应竞争指数分别为0.8~0.9、1.0~1.1、大于1.2,并据此确立了3 个经营方向。基于修正后的树冠生长模型编制的“树冠半径—林分密度”经营密度表,森林经营单位可以直观地将林分树冠半径生长现状和培育目标进行对比,从而及时调整经营策略。
北京地区的油松林多为人工栽植且立地条件相对单一,虽然研究选取的样地数量足够代表北京市油松人工林的基本情况,但由于研究区域的局限性,所得出的结论仅适用于北京地区的油松风景林经营,而其他地区因立地条件、油松品种等差异可能无法适用本研究编制的经营密度表。目前关于风景林合理密度的研究多集中于单一树种层面,而随着城市森林的发展,营造多树种混交的生态功能完备的森林已成为主要发展趋势[34]。为了更好地营建城市森林,今后需要对兼顾生态服务功能和景观要求的多树种混交林的密度表进行更加深入的研究。
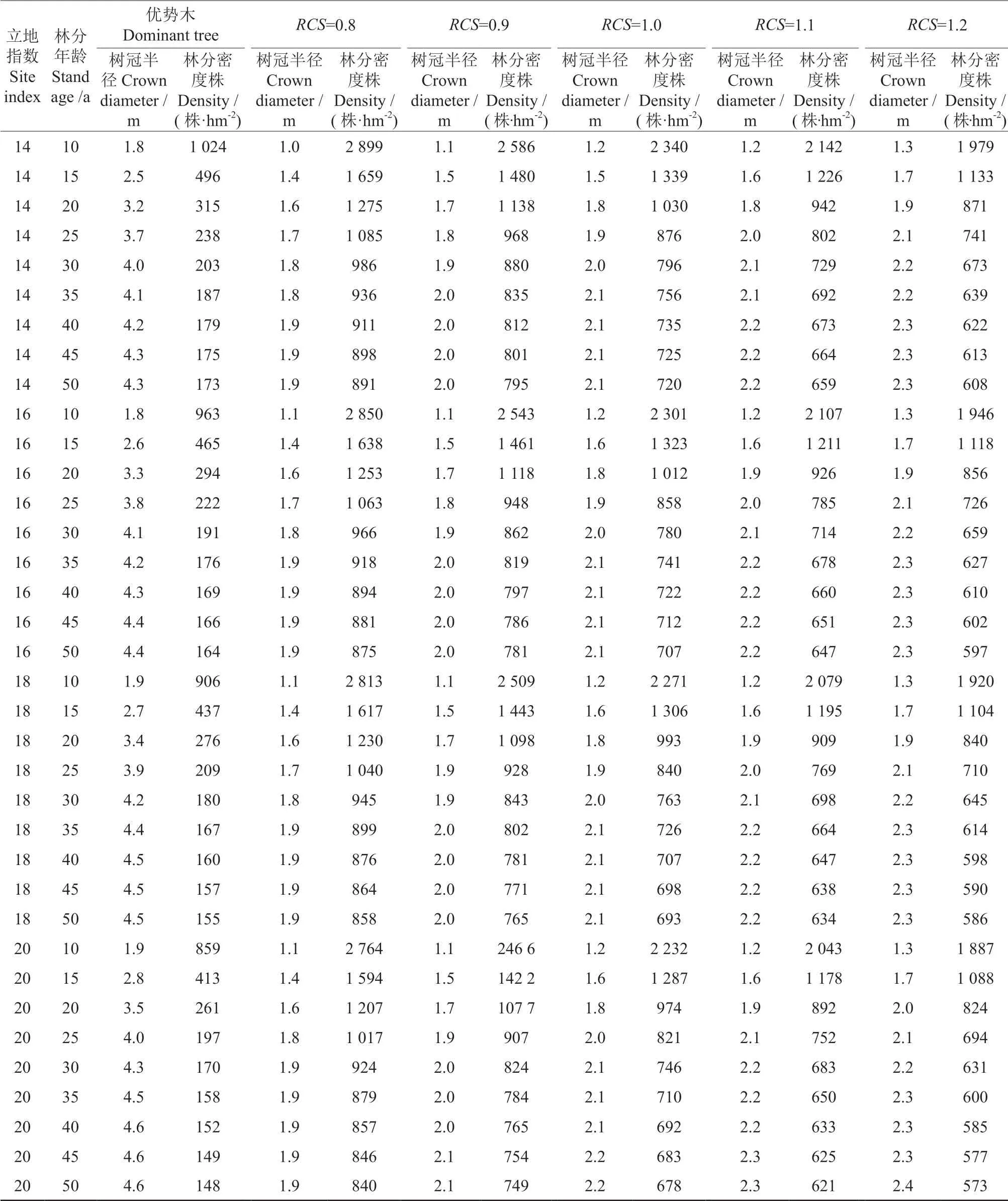
续表8Continuation of table 8
5 结论
树冠对林分密度和空间竞争的敏感性最强,相同的立地条件和年龄的林分中,林分密度越大,空间竞争越激烈,树冠生长受到的影响越大。基于树冠半径生长模型建立的林分经营密度表,可以直观地展现不同竞争强度的油松人工林在各年龄阶段的树冠半径和适宜的林分密度。风景林经营实践中应按照不同培养目标选择合适的林分密度和竞争强度。开发封闭式观赏景观,宜选择竞争指数为0.8~0.9 的中、高林分密度;培育观赏型林内景观时,宜选择竞争指数为1.0~1.1 时的林分密度;培育观赏型林内景观和开放式林下休闲空间时,应控制竞争指数大于等于1.2。
