考虑残余应力的焊接节点疲劳寿命有限元分析

何余良 钱昕 叶肖伟 张治成

摘 要：為研究残余应力对焊接结构疲劳性能的影响，基于热力耦合计算方法建立了热弹塑性有限元模型，模拟T型节点焊接全过程及焊后热处理的温度场与应力场。基于扩展有限元法建立T型焊接节点断裂力学数值模型，将焊接应力场作为初始条件引入模型并分析其对疲劳裂纹动态扩展行为的影响。结果表明，未考虑残余应力时，焊接节点疲劳裂纹向焊缝两端均匀发展，裂纹扩展形式与试验结果不符;焊后热处理可以显著降低焊接产生的高拉伸应力和压缩应力，但对疲劳寿命的增幅较小，仅为6.1%;考虑残余应力后疲劳裂纹扩展路径与试验更为接近，焊接结构有限元模拟应考虑焊接残余应力对疲劳裂纹扩展路径的影响。

关键词：焊接节点;疲劳寿命;扩展有限元;残余应力;焊后热处理

中图分类号：TU391;TG405   文献标志码：A   文章编号：2096-6717（2022）03-0054-08

收稿日期：2021-04-15

基金项目：国家自然科学基金（51822810、51778574）;浙江省自然科学基金（LR19E080002）;浙江省建设科技基金（2020K127）

作者简介：何余良（1977- ），男，博士，副教授，主要从事组合桥梁力学性能分析研究，E-mail： hyliang88888@163.com。

叶肖伟（通讯作者），男，教授，博士生导师，E-mail： cexwye@zju.edu.cn。

Received：2021-04-15

Foundation items：National Natural Science Foundation of China （No. 51822810， 51778574）; Natural Science Foundation of Zhejiang Province （No. LR19E080002）; Construction Science and Technology Fund of Zhejiang Province （No. 2020K127）

Author brief：HE Yuliang （1977- ）， PhD， associate professor， main research interest： analysis of mechanical properties of composite bridges， E-mail： hyliang88888@163.com.

YE Xiaowei （corresponding author）， professor， doctorial supervisor， E-mail： cexwye@zju.edu.cn.

Finite element analysis of fatigue life of welded joint considering residual stress

HE Yuliang1， QIAN Xin1， YE Xiaowei2， ZHANG Zhicheng2

（1. School of Civil Engineering， Shaoxing University， Shaoxing 312000，Zhejiang， P. R. China; 2. College of Civil Engineering and Architecture， Zhejiang University， Hangzhou 310058， P. R. China）

Abstract： In order to study the influence of residual stress on the fatigue performance of welded structures， a thermo-elastoplastic finite element （FE） model was established via thermal coupling method to simulate the temperature field and stress field during both the whole T-joint welding process and the post-welding heat treatment process. Based on the extended FE method， the numerical model of fracture mechanics of T-shaped welding joints was established. The initial condition of welding stress field was introduced into the model and its influence on the dynamic propagation behavior of fatigue cracks was analyzed. The results show that when residual stress is not taken into account， the fatigue crack of welding joint develops uniformly at both ends of the welding seam， and the crack propagation pattern is not consistent with the experiment. Post-welding heat treatment can significantly reduce the high tensile stress and compression stress generated by welding， but the increase of fatigue life span is less significant， at only 6.1%; considering the residual stress， the fatigue crack growth path is more consistent with the experiment. The influence of welding residual stress on the fatigue crack growth path should be considered in FE simulation of welded structure.

Keywords： welded joint; fatigue life; extended finite element; residual stress; post-weld heat treatment

焊接工艺因其经济便利等特点被广泛应用于各类工程结构的连接[1-2]。然而，焊接结构往往存在初始缺陷，导致疲劳问题显著[3]。目前，针对焊接节点疲劳寿命的研究方法主要有两种：一种是基于S-N曲线的传统疲劳分析方法[4-5];另一种是基于裂纹扩展速率公式的断裂力学方法[6-7]。扩展有限元方法在断裂力学方法的基础上，凭借无需进行网格重划分和预测裂纹扩展路径的优点，成为疲劳分析的主要方法之一。

由于焊接过程中加热和冷却过程不均匀，焊接接头会产生残余应力和不均匀的微观结构[8]。而焊接残余应力往往是导致焊接结构疲劳破坏的主要原因[9-10]，因此，对残余应力的研究一直是热点。Lee等[11]建立了基于循环塑性本构方程的三维热弹塑性有限元模型，评估循环荷载下的应力重分布情况，预测残余应力的周期性松弛。王春生等[12]在断裂力学数值模型中引入焊接残余应力场，分析其对正交异性钢桥面板疲劳裂纹静、动态扩展行为的影响。Jiang等[13]基于对残余应力的试验测量，分析了循环荷载下残余应力重分布的机理和对疲劳性能的影响，提出了焊接接头疲劳预测模型。实际工程中，为提高焊接结构的疲劳性能，往往会对焊接结构进行消除残余应力处理。焊后热处理工艺作为一种有效消除残余应力的方法被广泛应用于各类焊接结构[14]。许多学者对焊后热处理工艺消除残余应力开展了数值计算和试验研究。Venkata等[15]以P91钢对接接头为研究对象，建立数值模型模拟了不同热处理参数对对接接头残余应力的消除情况并进行试验验证。Mitra等[16]通过有限元和试验方法确定了温度和时间对应力释放的影响，并建立了热处理参数与残余应力的关系函数，以达到不同温度和时间组合实现相同的应力释放。逯世杰等[17]模拟了焊接过程及焊后热处理的应力场，并研究了蠕变效应在焊接过程中的作用，分析了焊后热处理消除残余应力的机理。Pokorny′等[18]提出了在外部荷载与残余应力条件下车轴的疲劳寿命评估方法，并分析了热处理对结构的影响。现有对热处理后疲劳性能的研究多以圆形结构为主，T型节点结构相对复杂，热处理操作困难，对T型节点的热处理和疲劳性能研究相对较少。因此，有必要建立T型焊接结构疲劳分析模型，研究热处理工艺对焊接结构疲劳性能的影响。

采用直接耦合热力分析法，建立T型焊接节点的热弹塑性数值模型，进行T型焊接节点的残余应力分析;用热处理方法进行消除残余应力计算;基于线弹性断裂力学理论和扩展有限元方法，建立疲劳分析有限元模型并引入残余应力场，分别计算在不考虑残余应力、考虑残余应力及热处理消除残余应力情况下的疲劳寿命。

1 残余应力及热处理分析

1.1 焊接有限元模型

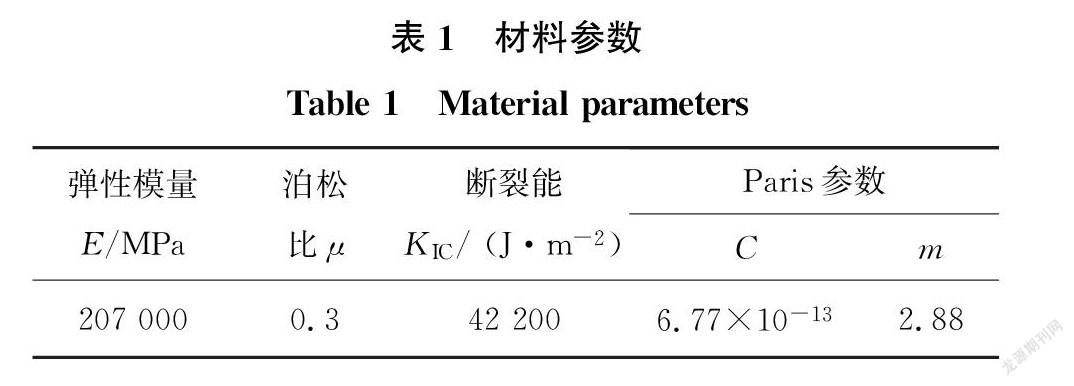
参考文献[19]的试验数据建立T型焊接接头疲劳有限元模型。T型接头由一块400 mm×100 mm×16 mm和一块200 mm×100 mm×15 mm钢板焊接而成，焊缝为全熔透焊缝。T型焊接节点尺寸如图1所示，焊缝简化为45°坡脚形式，建模为直角三棱柱。

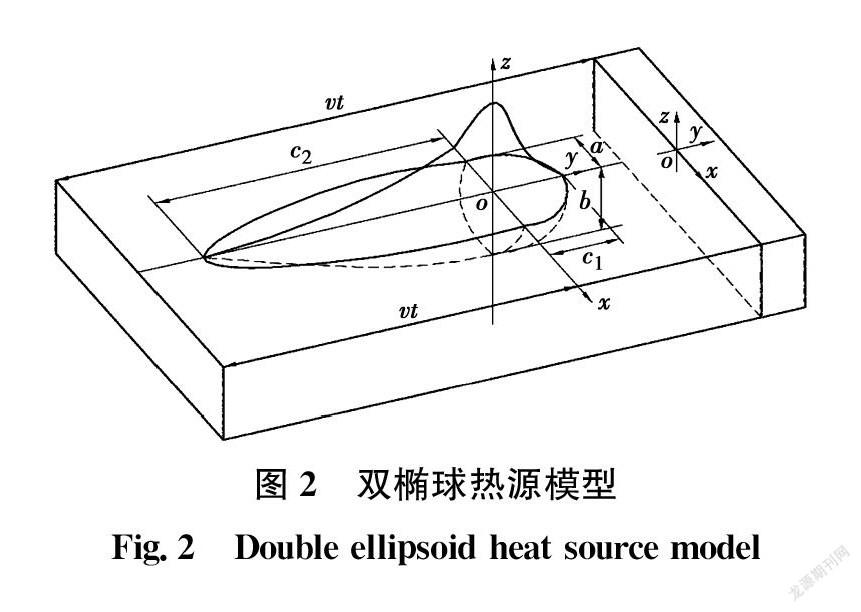
利用直接耦合的方式模拟焊接行为，即采用温度位移耦合分析步，单元类型采用八节点热耦合六面体单元（C3D8T）。热分析采用双椭球热源进行加热，热源模型如图2所示。对应的热源模型数学公式表示为

q=63fQπ3/2abcexp-3x2a2+y2b2+z2c2（1）

式中：q为热流密度，J/（m2·s）;f为热源移动函数;Q为单位时间热量，J;a、b、c为热源形状参数，取值分别为6、6、2.8、2.8 mm。

Q=η·U·I（2）

式中：η为焊接热效率;U为焊接电压，V;I为焊接电流，A。焊接电压取280 V，电流取25 A，热效率取0.8。热源焊接速度根据实际情况取为10 mm/s。采用dflux子程序控制热源在有限元模型上的移动。为简化计算，假定焊缝金属与母材具有相同的热物理和力学性能参数。焊接分析中钢材热物理与热力学参数主要参考文献[17]，如图3和图4所示。

1.2 焊接温度场分析

图5左侧图片为第1道焊缝焊接完成时焊缝区域的温度场，右侧为试验的熔池形貌。假设以图中1 420 ℃为熔点，焊缝区域和少部分母材处于熔化状态，对比文献[19]试验方法得到的焊接热影响区的熔池形貌，红色区域与试验结果较为接近。由此可推断，焊接有限元温度场与实际焊接结果大致相同，间接验证了有限元方法的合理性。

1.3 焊接应力场分析

以焊接温度场计算结果作为热荷载条件进行焊接应力计算。焊接时，由于焊接过程中的局部和瞬时加热以及整体冷却导致不均等的热传导和膨胀，冷却后接头局部区域发生弹塑性变形，产生较大的残余应力。图6中纵向残余应力与文献[17]的数值模拟和实测结果较为接近，说明残余应力数值模拟较为合理。

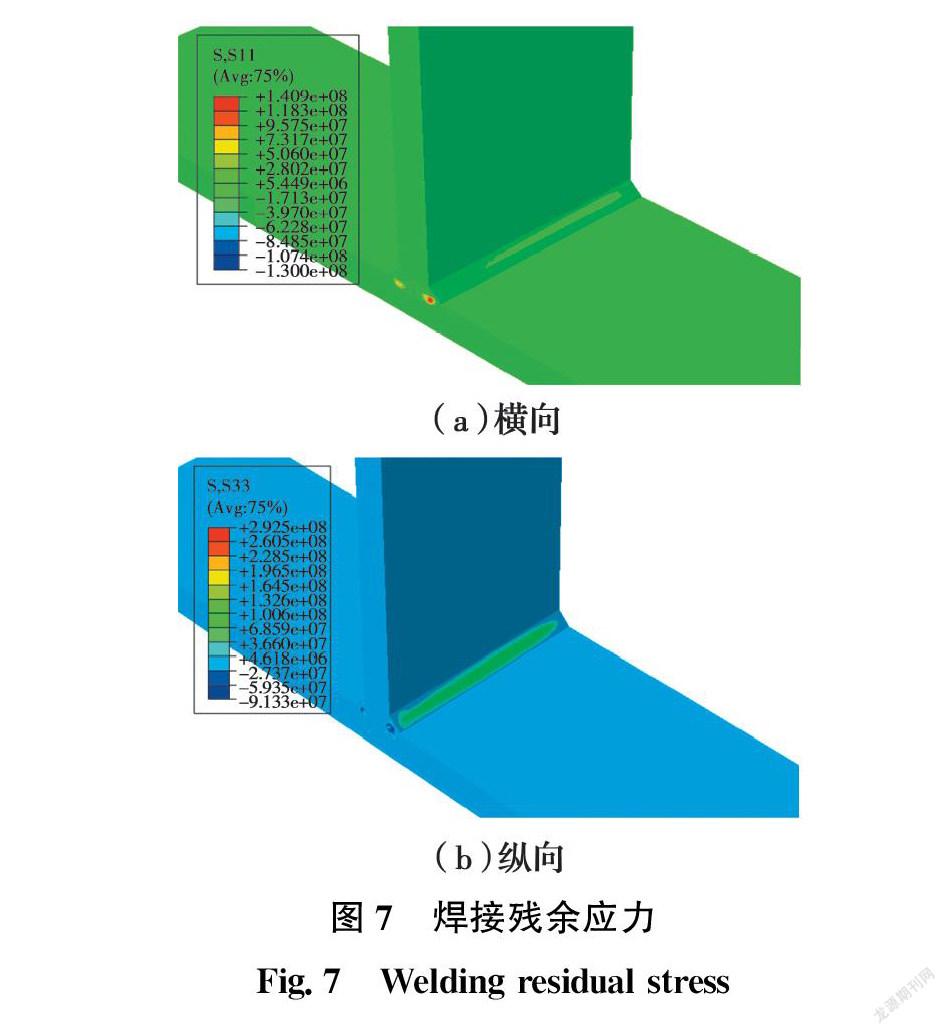
图7（a）显示了焊接模拟获得的横向焊接残余应力分布。焊缝起始和终止位置处于残余压应力状态，最大峰值压应力为130 MPa;焊缝中间区域處于残余拉应力状态，最大峰值拉应力为140.9 MPa。右方焊接残余应力分布范围略小于左方，这主要是因为，虽然焊接边界条件相同，但是由于焊接起始位置位于右方，导致约束条件和散热条件的不同，从而导致横向残余应力分布略有差异。

图7（b）显示了焊接模拟获得的纵向焊接残余应力分布。焊缝起始和终止位置处于残余压应力状态，最大峰值压应力为91.3 MPa;焊缝中间区域处于残余拉应力状态，最大峰值拉应力为292.5 MPa。

1.4 焊后热处理有限元模型

以计算得到的焊接残余应力作为初始条件进行焊后热处理过程的模拟计算。焊接并冷却至室温后，以20 ℃/min的速度将焊接节点加热至600 ℃，再保温30 min，最后进行炉冷，热处理曲线如图8所示。应力的释放主要通过两个机制，首先，由于计算过程使用了随温度变化的材料性能参数，故随着焊后热处理过程中温度的升高，材料的强度逐渐降低;其次，在热处理阶段考虑材料蠕变引起的塑性变形会导致应力松弛，且此阶段的蠕变服从Field & Field蠕变方程

εcr=atbσc（3）

式中：εcr为等效蠕变应变;t为时间，s;σ为等效应力;a、b、c取值参考文献[17]，a=-457+3.9T-0.01T2、b=11-0.09T、c=289-22.4T+0.006T2，T为与温度有关的常数。

1.5 焊后热处理分析

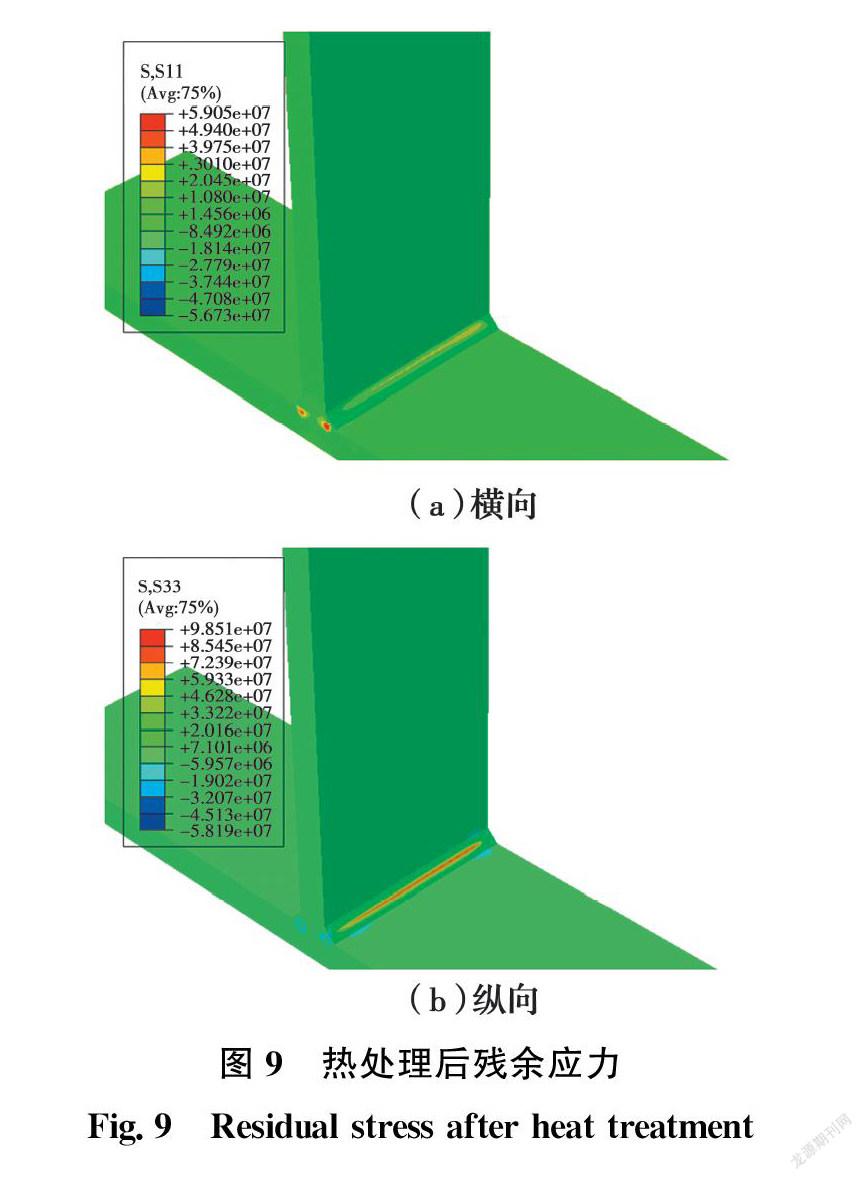
为定量研究经过焊接后热处理过程（PWHT）焊接残余应力的消除情况，提取热处理前后沿焊缝轴线上的横向和纵向残余应力进行对比分析。图9中残余应力与文献[17]的数值模拟和实测结果较为接近，说明热处理数值模拟较为合理。对比图7与图9，残余应力分布形式没有发生变化。经过焊接后热处理，拉伸残余应力的峰值大幅下降，但压缩残余应力的峰值变化不大，说明焊后热处理可以很好地消除由焊接产生的拉伸残余应力。横向残余应力的峰值由热处理前的140.9 MPa下降到59.1 MPa，下降了58.1%。纵向残余应力的峰值由热处理前的292.5 MPa下降到98.5 MPa，下降了66.3%。

2 热处理前后疲劳寿命分析

2.1 扩展有限元理论

Belytschko等[20]于1999年首次提出扩展有限元（XFEM）理论。该理论克服了有限元裂纹扩展对更新网格的需求。有限元位移公式引入富集函数，识别裂纹表面位移的跳跃和裂纹尖端的奇异性。

u（x）=NIuI+H（x）NI（x）aI+NI∑jFj（x）bjI（4）

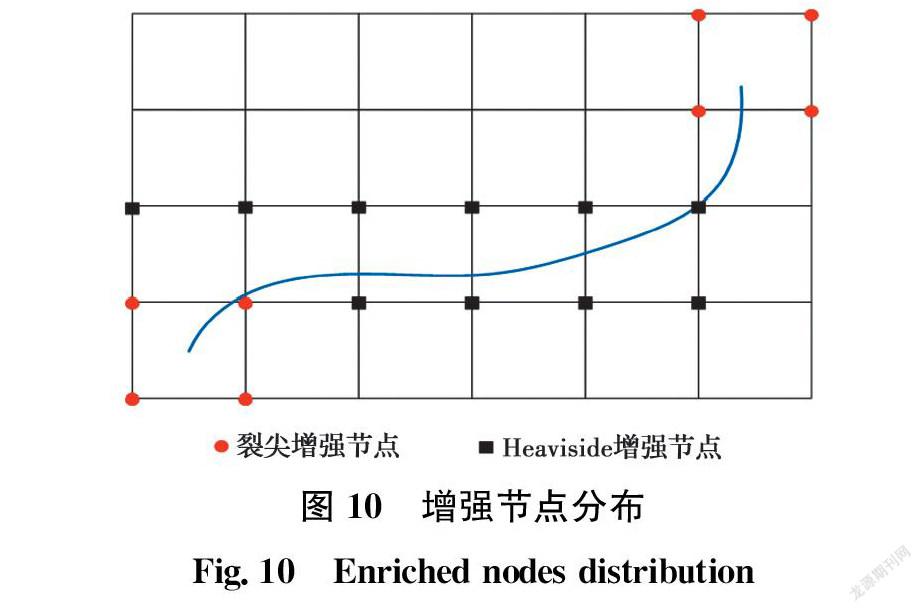
式中：u（x）为位移矢量;NI（x）为节点形函数;uI为节点位移矢量;H（x）为Heaviside函数;aI为考虑位移跳跃的增强节点自由度;Fj（x）为裂纹尖端函数;bIj为描述裂纹尖端的奇异性的节点自由度。对应的增强节点如图10所示。

Heaviside函数为

H（x）=1（x-x*）n≥0-1（x-x*）n<0（5）

式中：x为裂纹面任意点;x*为裂纹上最接近x的点;n为垂直于裂纹x*向外的单位矢量。

奇异函数Fj（x）为

Fj（x）=rsinθ2，rcosθ2，

rsin θsinθ2，rcos θcosθ2（6）

式中：r、θ为裂纹尖端局部坐标系极坐标。

2.2 疲劳裂纹扩展理论

Paris和Erdogan于1963年提出用于表达裂纹扩展的Paris公式

dadN=CΔKm（7）

式中：C和m为材料参数;a为裂纹长度;N为循环次数;ΔK=（Kmax+Kmin）/2，Kmax和Kmin为裂纹尖端最大和最小应力强度因子。

Paris公式可以表示为

dadN=c1ΔGc2（8）

式中：c1和c2为材料参数;ΔG为应变能释放率幅值，当裂纹尖端满足Gth<ΔG<Gpl時，裂纹开始扩展，Gth为能量释放率阈值，Gpl为能量释放率上限值。

2.3 疲劳有限元模型

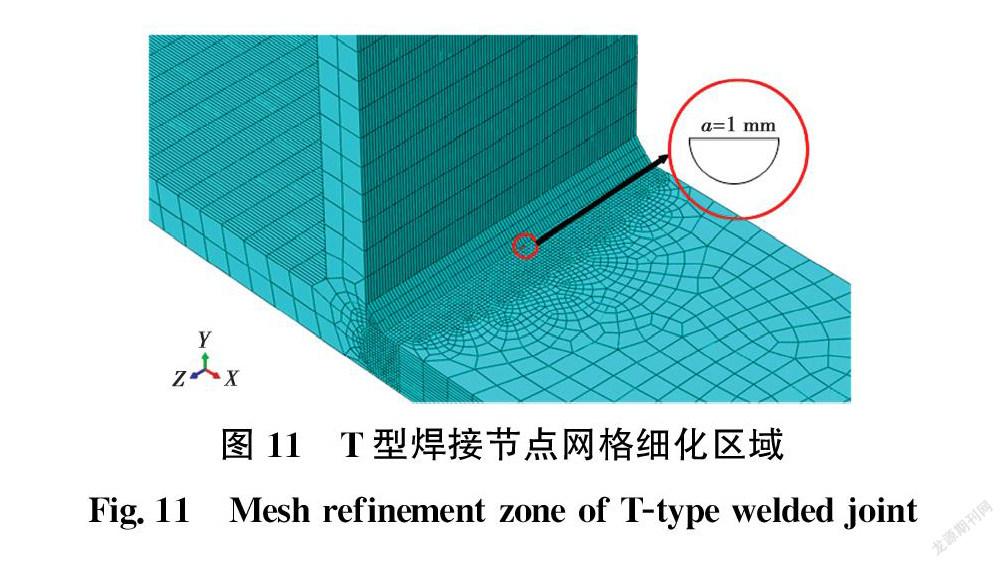
T型节点焊接有限元模型几何参数与疲劳有限元模型相同。在存在较大空隙的情况下，空隙形状（即长宽比）对整体疲劳寿命的影响很小[21]，故将初始裂纹模拟为a=1 mm的半圆形表面缺陷。通常，裂纹仅在腹板周围的两条焊缝中的一条上萌生并扩展，而另一侧的焊缝保持完整。因此，仅在其中一条焊缝上引入半圆形初始裂纹。

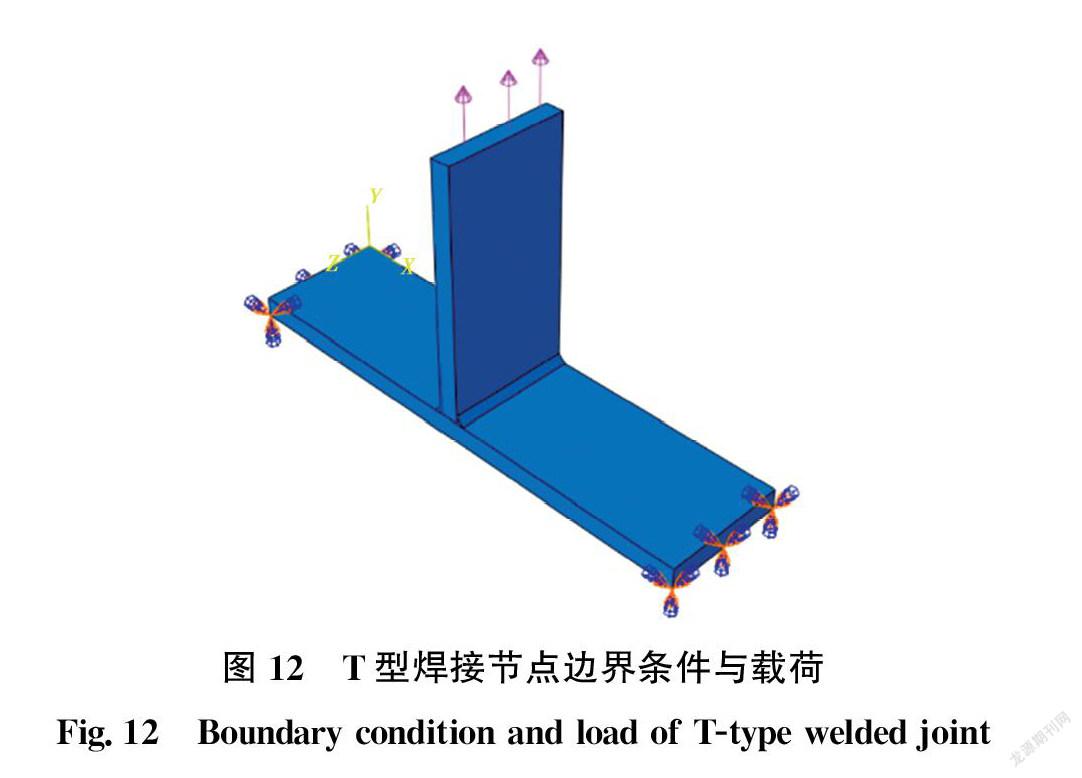
为节约计算量，对焊接接头进行局部加密处理。焊趾周围的单元尺寸为1 mm。远离焊趾的区域使用2、4 mm的单元尺寸（图11），单元总数为101 512。焊接钢的Paris常数为m=2.88和C=6.77×10-13 MPa·m1/2 [22]，并考虑了超强匹配接头对裂纹扩展率的影响[23]。其他材料参数如表1所示。T型节点腹板上方施加循环荷载，荷载为35 kN，应力比R=-1，频率为3 Hz。边界条件为两端固定（图12）。

2.4 不考虑残余应力疲劳寿命分析

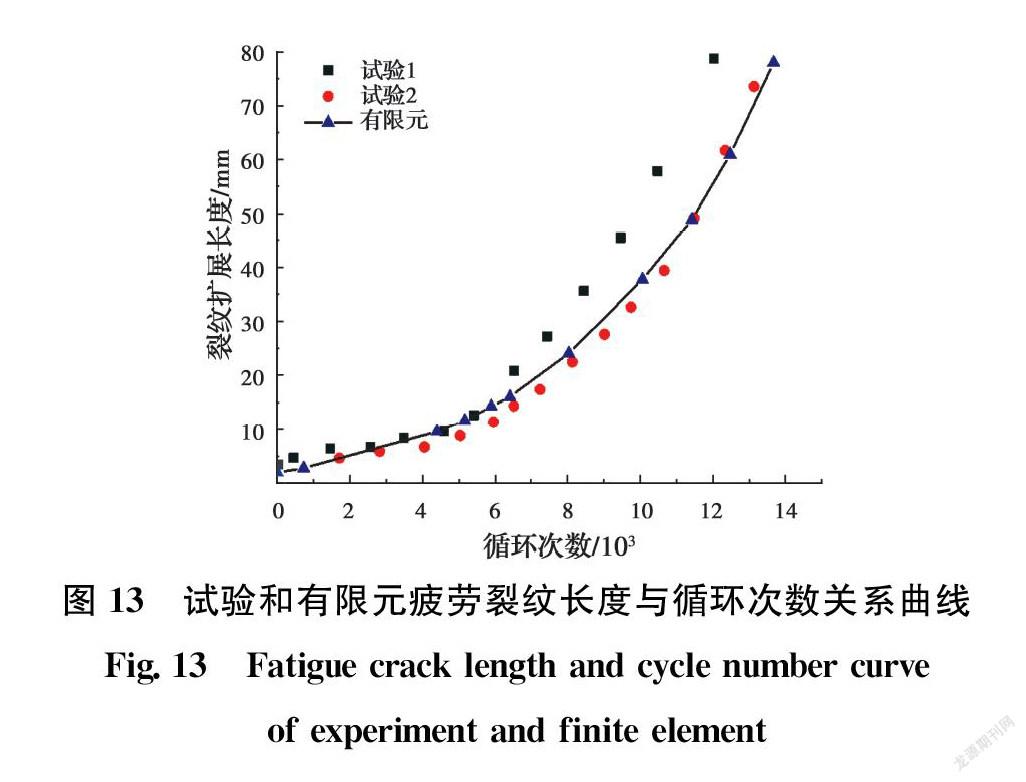
以裂纹深度达到钢板厚度（16 mm）的一半作为疲劳失效标准[19]。图13比较了试验结果[19]和XFEM计算结果。从图中可看到，两次试验平均失效循环次数为12 995，根据XFEM预测得出的失效循环次数为13 673（误差为+5%），XFEM得到的疲劳裂纹扩展预测结果与试验数据基本一致。试验数据和有限元结果略有差距，主要原因为：1）材料参数来源于贯穿裂纹扩展试验，而焊接对材料参数有一定影响; 2）在焊趾中间采用半圆形形状的初始裂纹，实际初始裂纹可能并不对称，也可能并非从焊趾中间萌生，或者有多个初始裂纹萌生并融合成一条裂纹。

2.5 热处理前后疲劳寿命分析

将焊接过程产生的残余应力、热处理后的残余应力作为初始条件，模拟得到不考虑残余应力、考虑焊接残余应力、热处理消除残余应力的T型焊接节点疲劳寿命如图14所示。三者的失效循环次数分别为13 673、12 078、12 812。考虑焊接残余应力的T型焊接节点相较于不考虑残余应力的模型疲劳寿命减少了11.7%，其疲劳扩展速率即裂纹长度与循环次数的比值相较于不考虑残余应力的模型更大，说明焊接残余应力加快了疲劳裂纹的扩展。热处理后T型节点疲劳寿命相比不进行热处理的T型节点疲劳寿命增加了6.1%，说明热处理对疲劳性能影响较小。其主要原因可能是热处理不仅会降低结构

的残余应力，而且对材料的性能也会产生相应的影响，材料性能的改变也会对结构的疲劳性能产生影响。残余应力的降低固然会导致疲劳强度的提高，但材料性能发生了改变，导致疲劳性能改变并不明显。裂纹扩展前期速度慢，后期速度变快，这可能是因为热处理虽然减小了焊缝中心区的高拉伸应力，前期疲劳扩展速率减小，但压缩应力也随之减小，后期疲劳裂纹更容易扩展。

图15展示了考虑残余应力的裂纹动态扩展情况。考虑残余应力和热处理的有限元模型疲劳寿命虽无显著变化，但和不考虑残余应力的模型相比，其疲劳扩展路径有较大区别。疲劳裂纹由不考虑残余应力时的中间向两端均匀发展变为一端扩展快而另一端扩展慢。其疲劳裂纹扩展路径与试验[19]得到的裂纹断面较为接近。产生该现象的原因为焊接残余应力的分布不均匀导致疲劳裂纹一端更易发展。

3 结论

考虑焊接残余应力及热处理对疲劳寿命的影响，建立T型焊接节点热弹塑性有限元模型和扩展有限元模型，分别进行残余应力、热处理和疲劳分析。研究结果表明：

1）未考虑残余应力时，T型焊接节点虽然疲劳寿命与试验较为接近，但疲劳裂纹向焊缝两端均匀扩展，裂纹扩展形式与试验不符。考虑残余应力后，疲劳裂纹变为一端扩展快而另一端扩展慢，扩展路径与试验更为接近。

2）经过600 ℃、30 min热处理后，T型焊接节点焊接残余应力得到充分消除，纵向残余应力峰值降幅为66.3%，横向残余应力峰值降幅为58.1%。

3）熱处理减小了焊缝中心区的高拉伸应力，前期疲劳扩展速率减小，但压缩应力也随之减小，后期疲劳裂纹更容易扩展。热处理后，T型节点疲劳寿命相比不进行热处理的T型节点疲劳寿命增加了6.1%。参考文献：

[1] 霍立兴. 焊接结构的断裂行为及评定[M]. 北京： 中国建筑工业出版社， 2000.

HUO L X. Fracture behavior and evaluation of welded structures [M]. Beijing： China Architecture & Building Press， 2000. （in Chinese）

[2] 田锡唐. 焊接结构[M]. 北京： 机械工业出版社， 1995.

TIAN X T. Welding structure [M]. Beijing： China Machin Press， 1995. （in Chinese）

[3] 黄云， 张清华， 郭亚文， 等. 钢桥面板纵肋与横隔板焊接细节表面缺陷及疲劳效应研究[J]. 工程力学， 2019， 36（3）： 203-213， 223.

HUANG Y， ZHANG Q H， GUO Y W， et al. Research on surface defects and fatigue effects at rib-to-crossbeam welded joints of orthotropic steel bridge decks [J]. Engineering Mechanics， 2019， 36（3）： 203-213， 223. （in Chinese）

[4] 叶肖伟， 傅大宝， 倪一清， 等. 考虑多因素共同作用的钢桥焊接节点疲劳可靠度评估[J]. 土木工程学报， 2013， 46（10）： 89-99.

YE X W， FU D B， NI Y Q， et al. Fatigue reliability assessment of welded joints in steel bridges considering multiple effects [J]. China Civil Engineering Journal， 2013， 46（10）： 89-99. （in Chinese）

[5] 王春生， 翟慕赛， Houankpo TON. 正交异性钢桥面板典型细节疲劳强度研究[J]. 工程力学， 2020， 37（8）： 102-111.

WANG C S， ZHAI M S， TON H. Fatigue strength of typical details in orthotropic steel bridge deck [J]. Engineering Mechanics， 2020， 37（8）： 102-111. （in Chinese）

[6] RAO S S D， RAJU S. Orthogonalized Generalized Iso-Geometric Analysis （OGIGA） and its applications to problems of fracture mechanics [J]. Computer Methods in Applied Mechanics and Engineering， 2020， 372： 113427.

[7] 李强， 王波. T型焊接接头疲劳裂纹应力强度因子的3D边界元计算[J]. 重庆建筑大学学报， 2000， 22（6）： 29-33.

LI Q， WANG B. 3D BE analysis on stress intensity factor of a fatigue crack in a welded T-joint [J]. Journal of Chongqing Jianzhu University， 2000， 22（6）： 29-33. （in Chinese）

[8] HU M J， LI K J， LI S L， et al. Stress relief investigation using creep model considering back stress in welded rotor [J]. Journal of Constructional Steel Research， 2020， 169： 106017.

[9] 王若林， 李根森. 扁平钢箱梁U肋焊接残余应力数值模拟分析[J]. 土木建筑与环境工程， 2015， 37（1）： 104-111.

WANG R L， LI G S. Numerical simulation for the residual stress of U-rib welding onto the flat steel box girder [J]. Journal of Civil， Architectural & Environmental Engineering， 2015， 37（1）： 104-111. （in Chinese）

[10] LOPEZ-JAUREGI A， ESNAOLA J A， ULACIA I， et al. Fatigue analysis of multipass welded joints considering residual stresses [J]. International Journal of Fatigue， 2015， 79： 75-85.

[11] LEE C H， CHANG K H， DO V N V. Finite element modeling of residual stress relaxation in steel butt welds under cyclic loading [J]. Engineering Structures， 2015， 103： 63-71.

[12] 王春生， 翟慕赛， 唐友明， 等. 钢桥面板疲劳裂纹耦合扩展机理的数值断裂力学模拟[J]. 中国公路学报， 2017， 30（3）： 82-95.

WANG C S， ZHAI M S， TANG Y M， et al. Numerical fracture mechanical simulation of fatigue crack coupled propagation mechanism for steel bridge deck [J]. China Journal of Highway and Transport， 2017， 30（3）： 82-95. （in Chinese）

[13] JIANG W C， XIE X F， WANG T J， et al. Fatigue life prediction of 316L stainless steel weld joint including the role of residual stress and its evolution： Experimental and modelling [J]. International Journal of Fatigue， 2021， 143： 105997.

[14] 溫志刚， 靳伟亮， 张剑利， 等. 焊后热处理对DH36钢焊接接头断裂韧性的影响[J]. 焊接学报， 2013， 34（3）： 89-92， 117.

WEN Z G， JIN W L， ZHANG J L， et al. Influence of post weld heat treatment on fracture toughness of DH36 steel welded joints [J]. Transactions of the China Welding Institution， 2013， 34（3）： 89-92， 117. （in Chinese）

[15] VENKATA K A， KUMAR S， DEY H C， et al. Study on the effect of post weld heat treatment parameters on the relaxation of welding residual stresses in electron beam welded P91 steel plates [J]. Procedia Engineering， 2014， 86： 223-233.

[16] MITRA A， SIVA PRASAD N， JANAKI RAM G D. Influence of temperature and time of post-weld heat treatment on stress relief in an 800-mm-thick steel weldment [J]. Journal of Materials Engineering and Performance， 2016， 25（4）： 1384-1393.

[17] 逯世杰， 王虎， 戴培元， 等. 蠕变对焊后热处理残余应力预测精度和计算效率的影响[J]. 金属学报， 2019， 55（12）： 1581-1592.

LU S J， WANG H， DAI P Y， et al. Effect of creep on prediction accuracy and calculating efficiency of residual stress in post weld heat treatment [J]. Acta Metallurgica Sinica， 2019， 55（12）： 1581-1592. （in Chinese）

[18] POKORN P， DLH P， PODUKA J， et al. Influence of heat treatment-induced residual stress on residual fatigue life of railway axles [J]. Theoretical and Applied Fracture Mechanics， 2020， 109： 102732.

[19] NIKFAM M R， ZEINODDINI M， AGHEBATI F， et al. Experimental and XFEM modelling of high cycle fatigue crack growth in steel welded T-joints [J]. International Journal of Mechanical Sciences， 2019， 153/154： 178-193.

[20] BELYTSCHKO T， BLACK T. Elastic crack growth in finite elements with minimal remeshing [J]. International Journal for Numerical Methods in Engineering， 1999， 45（5）： 601-620.

[21] YADOLLAHI A， MAHMOUDI M， ELWANY A， et al. Fatigue-life prediction of additively manufactured material： Effects of heat treatment and build orientation [J]. Fatigue & Fracture of Engineering Materials & Structures， 2020， 43（4）： 831-844.

[22] Guide to methods for assessing the acceptability of flaws in metallic structures： BS7910 [S]. London： British Standards Institution， 2005.

[23] SARZOSA D F B， GODEFROID L B， RUGGIERI C. Fatigue crack growth assessments in welded components including crack closure effects： Experiments and 3-D numerical modeling [J]. International Journal of Fatigue， 2013， 47： 279-291.

（编辑 王秀玲）