基于时序分解的微服务调用链根因定位*
2022-03-01韦强申董昭阳叶晓舟欧阳晔
宋 勇,韦强申,董昭阳,叶晓舟,欧阳晔,3
(1.北京大学,北京 100080;2.亚信科技(中国)有限公司,北京 100193;3.广州亚信技术有限公司,广东 广州 511400)
0 引言
如今,越来越多的应用程序使用微服务架构[1]。微服务架构将单体应用切分成多个独立的微服务,这些微服务具有独立开发、独立部署、责任单一等优点,使得整个系统更可靠、可扩展、更具弹性[2]。
然而,微服务的规模数量巨大,且依赖关系复杂,例如,腾讯微信系统有超过3 000个微服务[3];Netflix有大约500个微服务,日均处理20亿应用请求[4]。因此,当一个微服务出现故障的时候,故障会沿着微服务的依赖关系传播,从而引起大规模服务异常,使得微服务系统性能大大降低。此外,容器实例可以按照需求动态地创建和销毁,使得系统具有高度的动态性和复杂性。因此,为保证系统运行的性能,快速检测故障和定位根因仍然是一项艰巨的任务。
通过分析现有文献发现,目前已经有大量关于故障检测和根因定位的方法,包括基于非结构化日志的故障检测方法[5-6]、基于系统关键性能指标的故障检测方法[7-8]、基于调用链日志的异常服务检测方法并做根因分析[9-11],以及比较流行的通过构造故障传播图实现的根因定位方法[12]。由于有些故障并不会严格按照节点调用的某一个方向传播,且并不一定会体现在前端节点上,或者由于其他因素影响,有些统计相关性高的指标实际并不一定具有很大的相关性;因此,使用以上方法不一定能够实现较好的根因定位效果。
本文提出了一种基于调用链时序分解的微服务根因定位方法StudRank,该方法的前提是,需要对前端性能指标做异常检测,一旦发现异常,才会启动StudRank的根因分析。具体而言,首先对调用链数据做预处理,计算节点的调用耗时,并且解析成含有调用关系的时序数据;其次对调用关系的指标做时序的异常检测,如果为异常,则把节点标记为异常;再次在动态构建的拓扑图中,萃取含有异常节点的异常子图;最后构造异常传播的概率转移矩阵,应用随机游走算法PageRank对异常节点打分排序。使用2020AIOps挑战赛公开数据集[13]对本文所提方法进行实验与测试。实验结果表明,所提方法在top1的精确度达到了84%,并与微服务根因分析经典方法进行了对比,较其中效果最好的MicroRCA准确度提升了97.6%。
本文的其余部分安排为:第1节讨论相关工作,第2节详细介绍StudRank方法,第3节描述实验评估,第4节总结全文。
1 相关工作
目前已经有许多关于微服务分布式系统的故障检测和根因定位研究。总的来说,这些研究提出的方法分为基于非结构化日志分析的方法、基于系统关键性能指标的方法、基于调用链日志的方法以及构建故障传播图的方法。
1.1 基于非结构化日志的方法
非结构化日志分析的方法是一种常用的系统异常检测方法。LogDC[5]是一种基于日志模型的问题诊断工具,其使用非结构化日志分析方法对Kubernetes的云应用程序进行异常检测。Jia等人[6]提出了一种基于日志的自动异常检测方法,构建了一个能够捕获服务间和服务内的正常执行流程的混合模型,如果观察到的与模型存在偏差,则发出异常告警。然而这种非结构化文本日志分析方法,很难进行因果关系推导,因此不太适用于故障根因定位。
1.2 基于系统关键性能指标的方法
系统关键性能指标,指的是系统节点(物理机、虚拟机、应用等)的CPU、内存、磁盘等相关的性能指标。很多方法通过分析性能指标来定位根因,例如,Sieve方法[7]首先过滤掉不重要的指标来降低指标的维度,其次基于格兰杰因果关系检验,分析组件之间的度量依赖关系,得到异常的根因;MicroRCA方法[8]通过将应用程序性能症状与相应的系统资源利用率相关联来实时推断根本原因,这种根因定位方法基于一个属性图,该图对跨服务和机器的异常传播进行建模。然而,这些方法仅通过分析指标的相关性来推断服务是否异常,并不能准确地判定根因结果。
1.3 基于调用链日志的方法
当前已经有很多记录调用链日志的跟踪工具和系统[14-17],如TraceAnomaly模型[10]基于调用链数据构造服务的跟踪向量,然后通过深度贝叶斯网络学习跟踪向量分布,如果检测的跟踪向量不符合分布,则会被认为是异常;Seer模型[9]通过神经网络来分析调用链日志,并基于卷积神经网络模型过滤掉不影响性能的调用链节点,然后使用长短期记忆网络(Long Short-Term Memory,LSTM)学习时间和空间模式,来分析服务质量;TraceRank模型[11]利用调用链数据的信息构造异常传播图,并引入频谱分析和基于PageRank的随机游走方法来检测异常服务。但是深度学习方法需要消耗大量的计算资源,并需要对不同的调用链模式建模,当系统发生改变的时候,会导致模型效果大大降低,且构造图的方法需要遍历所有的服务节点,因此,对于一个超大型的微服务系统来说,基于调用链日志的方法是低效的。
1.4 构建故障传播图的方法
软件架构经历了从单体架构到微服务的转变,以实现软件开发的弹性、敏捷性和可扩展性,进而构建故障传播图来定位故障根因。MicroHECL根因定位方法[12]基于动态构建的服务调用图分析可能的异常传播链,并基于相关性分析对候选根本原因进行排序。但是由于有些故障并不会严格按照节点调用的某一个方向传播,且并不一定会体现在前端节点上,或者由于其他因素影响,有些统计相关性高的指标实际并不一定具有很大的相关性;因此,使用这些方法不一定能够实现较好的根因定位效果。
2 StudRank概述
如图1所示,StudRank总体方案分为3个部分:数据预处理、指标异常检测和根因定位。
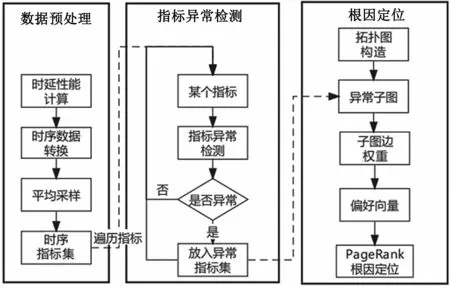
图1 StudRank流程
2.1 数据预处理
数据预处理需要把调用链数据转化为时序数据,并把调用链中节点的调用关系(父子节点对)挖掘出来组成时序数据序列。本节内容将详细介绍数据预处理的流程。
2.1.1 调用链数据的结构
调用链数据描述的是请求执行过程中,调用微服务记录的信息,其结构如图2所示。
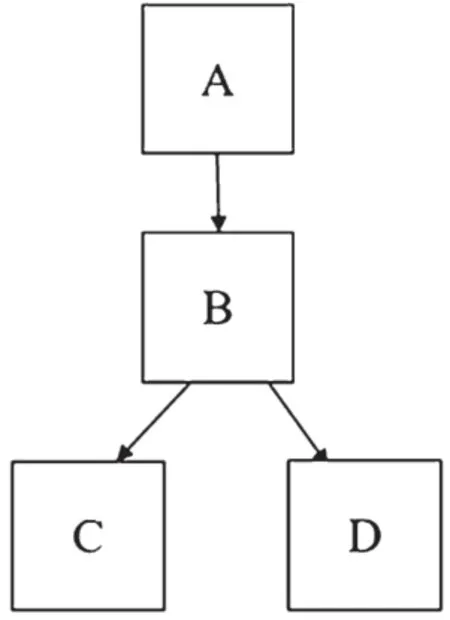
图2 某一次请求调用微服务的拓扑结构
每一次调用微服务一般会记录时间戳、微服务名称、响应时延、该次调用的唯一标识ID、上游节点ID,以及标识每一次用户请求的ID等信息。表1是某系统调用链数据的主要属性。

表1 某系统调用链数据的主要属性
2.1.2 计算节点的时延性能
图3展示的是某一次请求调用链的结构和日志信息,长方形代表调用链访问的微服务节点,记录了时间戳、节点名称和时延。
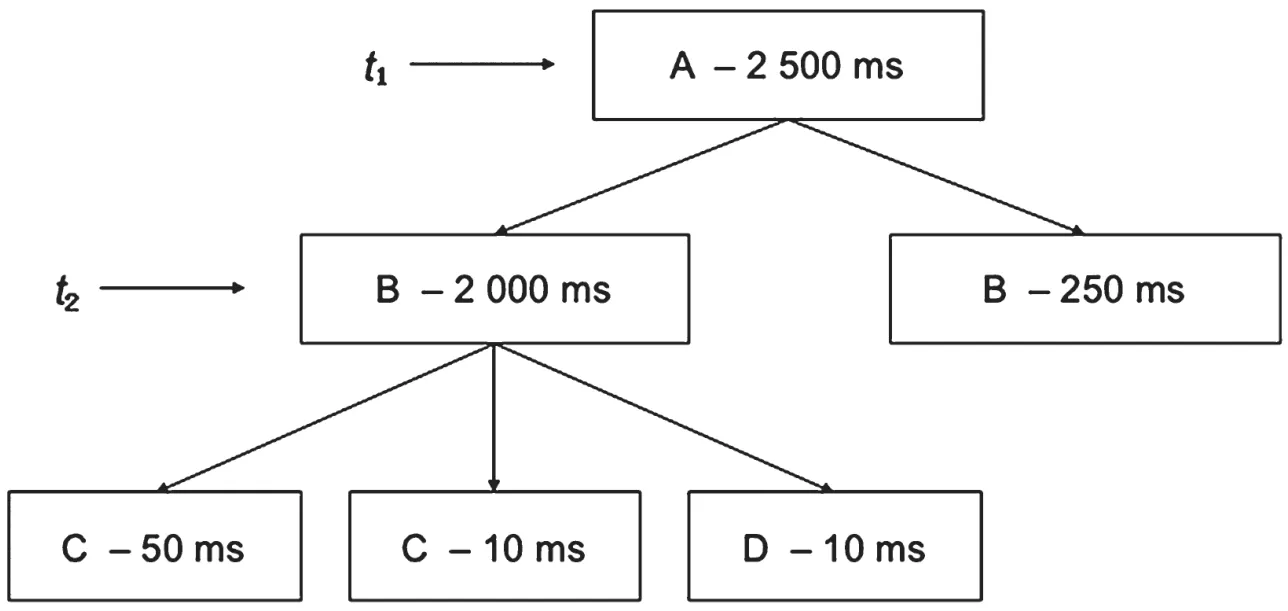
图3 某一个调用链路
定义t(N)代表节点N的时间损耗,t0(N)代表N调用子节点的时间损耗,即节点N的时延性能,t0(N)表达式为:
式中:Ni是N的下游节点。
计算节点的时延性能,是因为它能消除时延在有依赖关系节点的异常传播。如图3,节点A和B明显时延过大,有异常的症状。计算两个节点的时延性能t0(A)=250 ms。显然,B节点的异常症状没有传播到A节点。
2.1.3 构建结构向量
使用父节点时间戳、父节点、子节点、父节点时延性能构造1个4元组向量。定义向量为:
式中:t为调用链访问N节点的时间戳;N为调用链的某个节点;N1,N2,…,Nm为N的下游子节点。如图3,可以构建两个向量:(t1,A,[B],250),(t2,B,[C,D],1 930)。
2.1.4 构造时序数据
将向量转化为时序指标,父节点和任意一个子节点组成一个二元指标,式(2)可以转化为m个指标,分别为(N,N2),(N,N2)…,(N,Nm),t0(N)转化为指标在时间t的值。
对指标按照分钟平均采样。基于观察,如果一个节点出现故障,那么任意一个访问该节点的调用链或者包含该节点的指标对应的时延或时延性能值都会过大,即这样过大的值是占大多数的。对指标按照分钟采样取平均,节点的故障特征不会被消除。如果该节点没有故障,仅仅是同级节点故障造成的包含该节点的指标值过大,这样的点是少数,可以通过平均采样消除这些噪点的影响。
2.2 指标异常检测
对于待检测的时间点或者时间段,检测每一个指标在该检测时间下的值是否异常。采用核密度估计方法和差值法检测,具体如下文所述。
2.2.1 核密度估计方法
对于某个指标,取一段正常的历史数据,根据该数据,估计一个概率密度函数。如图4所示,直方图外面包裹的实线就是概率密度函数。
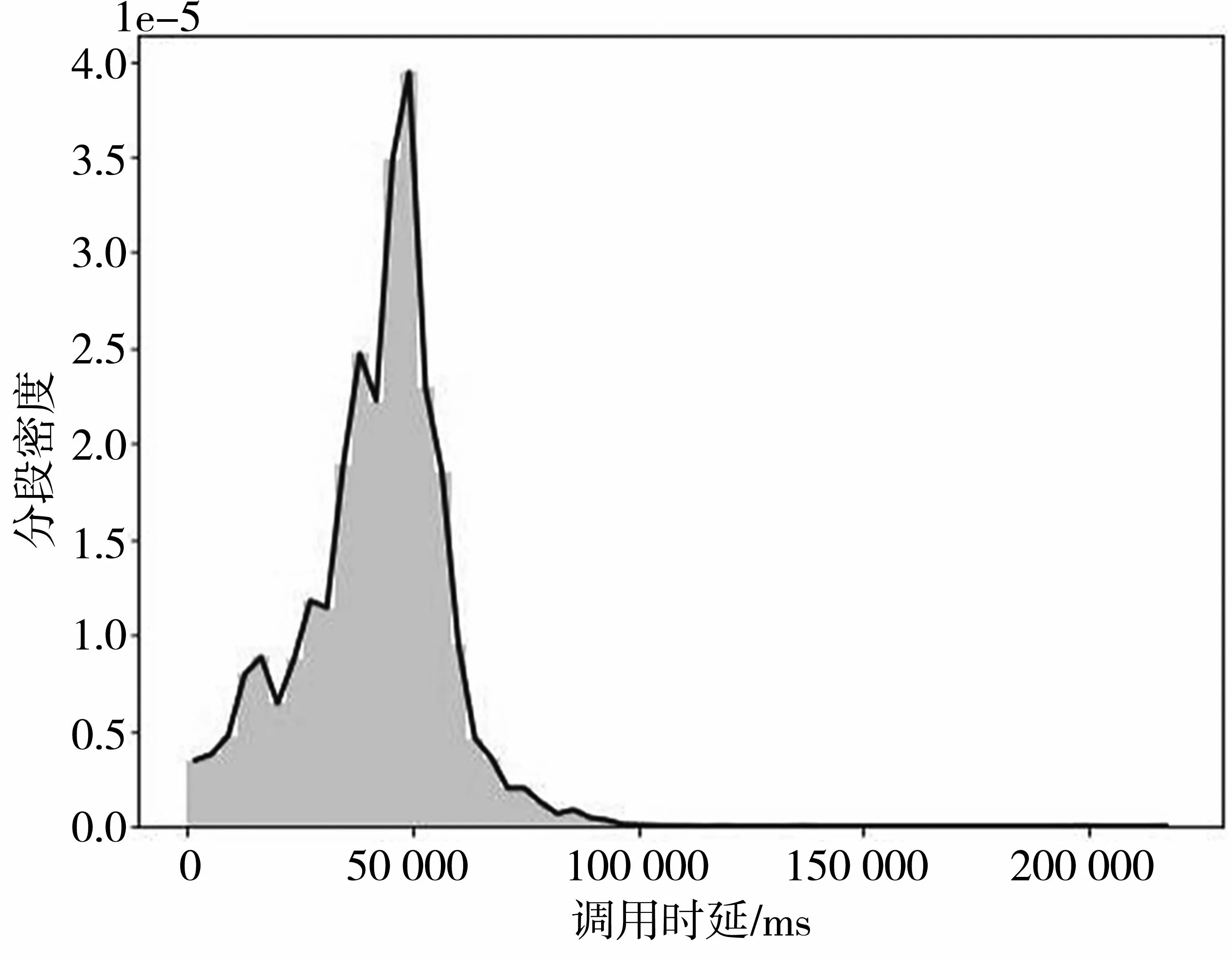
图4 单指标密度函数
对于待检测数据,计算检测值的累积概率,定义如下:
式中:x为连续型随机变量,为检测时间点指标对应的值,或者检测时间段指标对应的平均值;f(x)为概率密度;α为可调阈值。Pr值越小,表明越可能是异常。
2.2.2 差值法
定义x-是指标历史正常值的均值,σ是指标历史正常值的标准差,θ是大于0的调节因子。α是检测时间点指标对应的值,或者检测时间段指标对应的平均值,如满足式(4),则认为该指标是异常。
2.2.3 其他情况
如果时序指标在某一个时间点是空值,那么,所有的调用链访问这两个父子节点对都没有数据,据笔者观察,这是由被调用节点的故障导致的。
基于集成的方法中,如果核密度估计方法和差值法的结果都是异常,或者在检测窗口存在空值,那么指标就是异常。
异常检测算法的部分流程如下:

2.3 利用随机游走算法定位根因
通过2.1节和2.2节检测出了可疑的异常节点,但是,无法确定哪个节点更可能是根因。受文献[11]和文献[18-21]的启发,笔者考虑使用随机游走算法,即个性化的PageRank[22],对节点根因进行定位。
2.3.1 PageRank算法
PageRank算法最初是谷歌公司用于网页链接分析的算法,它可以对搜索引擎搜索的网页链接进行排序。其原理是根据网页链接的数量,对网页的重要性进行排名。该算法通过概率转移矩阵描述网页之间的链接,为了防止有些网站链接不出去,又设计了偏好向量。PageRank算法描述如下:
式中:π为节点(网页)重要性得分向量;P为概率转移矩阵;u为偏好向量;α∈[0,1],为阻尼因子。α越接近0,随机游走越以偏好向量访问节点;α越接近1,随机游走越以概率转移矩阵(图结构)访问节点。PageRank算法不仅可以用于网页重要性排名,也可以用于系统的故障根因定位,其中,作为节点的异常得分越大,则节点故障的可能性越大。
2.3.2 图的构造
在定位根因之前,需要构造异常传播图。由于观察到异常在调用路径上传播,可以根据调用链数据的动态构建异常传播图。构建过程如下:
(1)截取故障前一批调用链数据。数据包含了很多调用链,例如图5中的调用链1、调用链2、调用链3。
(2)确定图的节点。把调用链数据中包含的节点作为图节点,如图5所示的调用链数据中的节点A、B、C、D、E、F、G。
(3)确定图的边。如果调用链数据中,存在A节点调用B节点,那么在图中,可以赋予图节点A到B的有向边,表示节点A出现故障的原因是节点B出现了故障,例如图5中的A→B、A→C、B→D、B→E、B→F、C→G。
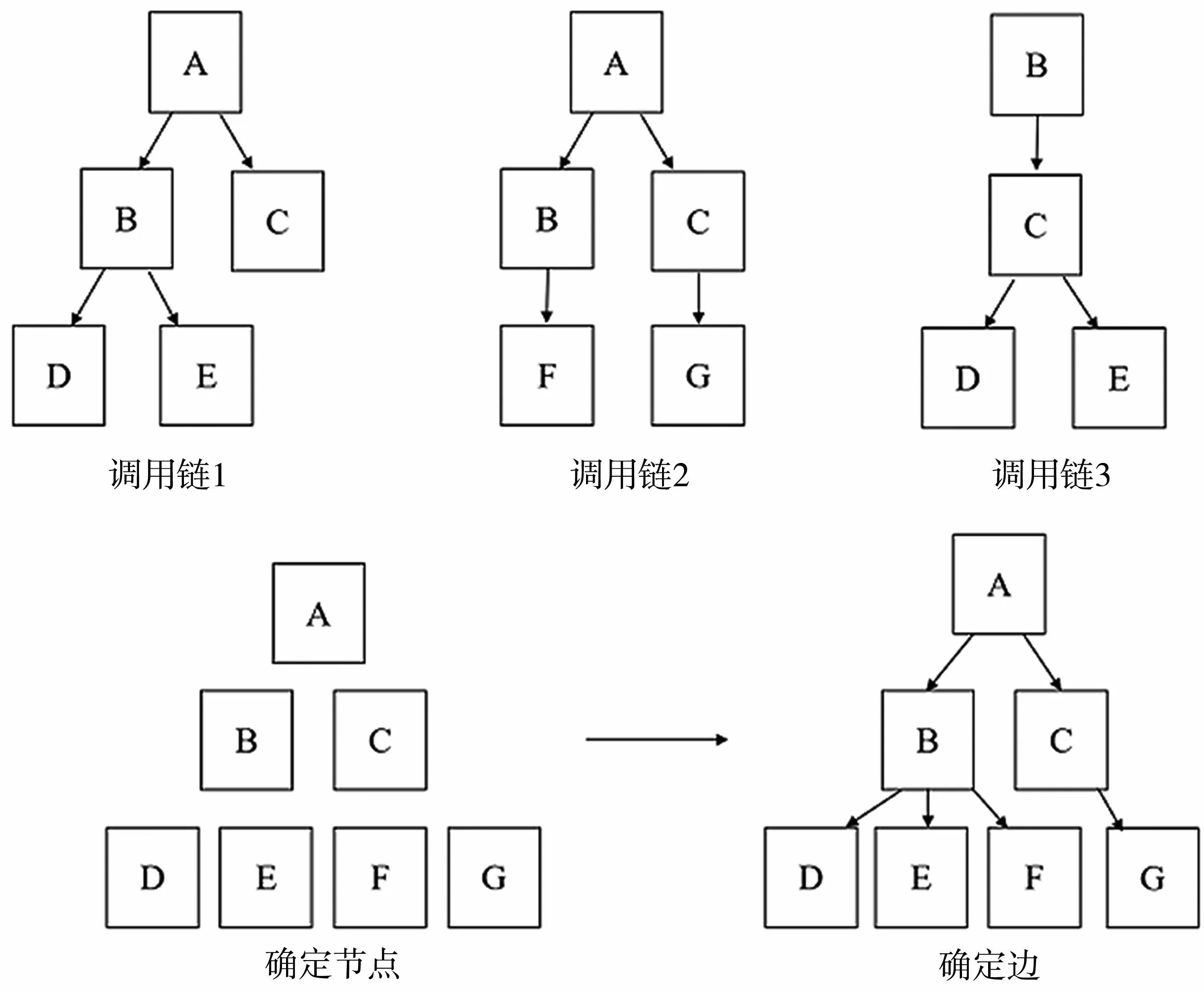
图5 异常传播图构造过程
总的来说,定义图G=<V,E>,V是微服务节点(调用节点)的集合,定义E代表有向边的集合,如果eij∈E,代表节点vi调用节点vj,即为vi到vj的有向边。
2.3.3 子图的萃取
如图6(a)所示,得到异常传播图后,还需要萃取异常子图,异常子图记为G'=<V',E'>。在2.1节数据预处理中,把调用链转化为多个时序指标数据,即父节点调用子节点的时序数据,而时序指标正好对应了故障传播图的边。把异常节点定义为异常时序指标对应边起始的两个节点。如图6(b)所示,检测到时序指标(A,B)、(B,E)、(B,F)是异常,则对应的虚线边就是异常,虚线边两边的节点A、B、E、F是异常节点。那么,提取异常节点和异常边作为子图,如图6(c)所示。

图6 子图萃取过程
2.3.4 子图边权重
得到异常子图G'=<V',E'>后,对于边ei'j∈E'的权重计算如下:
式中:x为2.2节中式(4)的差值;α和a为调节参数。使用该方法计算边的权重的原因是,节点的调用时延越大越可能是异常,而x是时延指标的偏移量,x越大,对应的Sij越大,就代表调用vj产生异常的概率也越大。
2.3.5 概率转移矩阵
随机游走算法将按照子图G'=<V',E'>游走,并且以Sij的概率前向游走。但是,由于环境的复杂性,子图并不足以描述异常的传播关系,例如,节点vi调用节点vj,对应检测出的时延性能值异常,既可能是vi故障的症状表现,也可能是vj故障的症状表现。因此,为了使结果具有鲁棒性,需要进一步定义随机游走算法的概率转移矩阵P。
(1)前向游走。如果eij∈E',那么vi调用vj产生的时延性能异常,很可能vj是异常的因,即故障由vj传播到vi,且权重Sij越大,传播的可能性也越大。由式(6)可知Sij∈[0,1],所以可以定义P的转移概率pij等于Sij,即:
(2)后向游走。对于eij∈E',且eji∉E',如果vi是异常的因,随机游走从vi以概率pij游走到vj,那么就再也无法游走到真正的根因了。因此,前向游走需要允许以一定的概率返回,则后向概率定义为:
式中:δ∈[0,1],为可调参数。
(3)其他游走。对于eij∉E',且eji∉E',考虑到系统的复杂性,可以赋予一个低的概率值,则定义:
结合前向游走、后向游走和其他游走,随机游走算法在子图G'=<V',E'>的概率矩阵定义为:
再对概率矩阵标准化,就可以得到概率转移矩阵P:
2.3.6 偏好向量
偏好向量代表的是节点的异常概率。从2.1节的式(1)可以看出,节点调用的时延性能消除了时延异常的传播依赖,因此如果节点出现故障,那么该节点调用或者被调用时出现时延性能异常症状的概率越大。在提取的异常子图中,节点的中心度越大,则越有可能是故障。因此,通过计算子图节点的中心度来代表节点的异常程度,节点vi的异常表示如下:
对节点的中心度归一化,就可以得到偏好向量为:
2.3.7 节点排名
综上,通过计算概率转移矩阵和偏好向量u,基于PageRank式(5),对节点异常得分向量π进行迭代,直到π趋于平稳,就是各个节点的最终得分,根据得分就可以判断故障根因。
3 实验评估
在这一部分,将使用2020国际AIOps挑战赛公开数据集评估的方法,将本文所提方法与硬编码、MircoRCA、MicroHECL 3种常用方法进行对比,最后将讨论所提方法的特征。
3.1 实验准备
3.1.1 数据
测试StudRank方法使用的数据是2020国际AIOps挑战赛公开的数据,该数据来源于某运营商真实生产环境。通过统计甄别公开的15天的数据,得到3种故障类型,分别为网络故障、CPU故障和数据库故障。本文实验只使用其中的调用链数据,并且实验方法只定位到调用链访问的节点,不考虑资源依赖的宿主机。
3.1.2 对比方法说明
本文采用的对比方法为硬编码、MircoRCA、MicroHECL,这3种方法的具体介绍如下文所述。
(1)硬编码
硬编码是将规则或数据直接嵌入到程序中的方法。设置指标的静态阈值,并根据设置的静态阈值产生的告警分析根因。使用该方法进行实验时,模拟静态阈值的方法,设置微服务调用时延的阈值为1 000 ms。超过阈值,则微服务为异常。再利用已知的拓扑关系定位根因。
(2)MircoRCA
该方法基于已知拓扑图关系,利用BIRCH算法计算服务的时延调用异常,并基于异常检测构建异常子图以及时延和性能指标的相关性计算子图边的权重,再利用个性化PageRank算法,对异常节点评分。本文使用该方法进行实验时,不考虑与调用无关的宿主机节点,在计算相关性的时候,不考虑容器或主机的网络指标。
(3)MicroHECL
该方法分为3个部分:首先根据待分析的时间窗口动态构建服务依赖图,其次采用剪枝策略分析异常传播链,最后基于皮尔森相关系数对候选根因排序。考虑到本文实验数据的特性,只分析服务的响应时间。在使用该方法进行实验时,使用和StudRank一样的方法做异常检测。
3.1.3 度量标准
为了度量算法在数据集的性能,将使用以下度量指标:
(1)排名前的精度,记为PR@K,指的是算法推断出的根因排名在前面的概率。定义:
式中:R为故障根因集合;r为某一个故障的根因集;f(i,r)的值为1或0,如果算法推理出的根因排名中的第i个在r里,为1;若不在r里,则为0。
(2)平均精度,记为AP,指PR@K的平均值,其表达式为:
式中:N为微服务的数量。
3.2 实验结果分析
表2、表3、表4和表5对比了StudRank与硬编码、MircoRCA、MicroHECL这3种方法对所有故障和各个类型故障的根因定位表现,并进行了具体的分析,其中,inf表示对比对象的值为0,提升幅度极大。

表2 StudRank与硬编码、MircoRCA、MicroHECL在故障集根因定位的效果对比

表3 StudRank与硬编码、MircoRCA、MicroHECL在网络故障根因定位的效果对比

表4 StudRank与硬编码、MircoRCA、MicroHECL在CPU故障根因定位的效果对比

表5 StudRank与硬编码、MircoRCA、MicroHECL在DB故障检测根因定位的效果对比
3.2.1 StudRank效果
算法StudRank在整个故障集R的评测指标中,PR@1达 到84%,PR@3,PR@5和AP都超过了92%。这在一定程度上体现了StudRank算法在调用链根因定位的优越性。在各种故障类型中,所提算法对CPU故障进行根因定位的效果最好,所有评测指标都达到100%。这是因为CPU故障会对服务的调用时延和被调用时延都产生影响,症状比较明显,根因很容易被检测到。对网络故障的根因定位效果仅次于对CPU故障进行根因定位的效果,除了PR@1外,其他指标都超过了90%。网络故障比CPU故障效果差,是因为某些根因没有在调用链节点上,比如os_001和os_009,数据中也没有微服务与这些宿主机节点的映射信息;因此,这类根因是无法推断出来的。表现最差的是针对DB故障的根因定位,这是因为有些故障不会体现在服务的调用时延上,这种基于调用时延的根因定位方法是无法检测出来的。
3.2.2 方法对比
在整个故障集R上进行实验的结果表明,StudRank相对于表现其次的MicroRCA,指标PR@1提升了97.6%,指标PR@3提升了21.2%,指标PR@5提升了16.4%,AP提升了13.8%。硬编码的效果最差,因为静态的阈值不能有效地捕获到异常。
在对网络故障数据进行根因定位的实验中,StudRank在所有的指标都表现得最好,指标值都在90%左右,相对于MicroRCA,StudRank的PR@1提升了69.30%,AP提升了6.5%。硬编码和MicroHECL的效果最差。
在对CPU故障数据进行根因定位的实验中,StudRank表现最好,所有指标都达到了100%,原因正如3.2.1节分析的那样。相对而言,MicroRCA除在PR@1指标上差了一些,其他指标都与StudRank接近。排除硬编码方法,MicroHECL表现得最差,PR@1和PR@3均低于14%。这是因为CPU故障的根因有些并不在拓扑链条的最下游或者最上游,这与MicroHECL的假设相违背了。
在对DB故障数据进行根因定位的实验中,如3.2.1节分析的那样,有些故障不会体现在服务的调用时延上,或者时延性能的症状并不明显。因此,基于相关性分析的MicroRCA和MicroHECL,很难捕捉到异常症状,其PR@1和PR@3不足8%。而StudRank不涉及相关性分析,基于核密度估计和差值统计量能够捕捉到微弱的异常症状,因此,StudRank方法的表现最好,PR@1达到了40%,PR@3达到了73.3%。
3.3 进一步讨论
StudRank是基于指标异常检测进行根因分析,那么,指标异常检测的质量在一定程度上影响了根因分析的结果。本节将进一步讨论核密度估计方法超参数和差值法超参数对结果的影响。
核密度估计方法检测质量受控于式(3)中的阈值α,即显著水平,如图7所示,其中,横坐标代表阈值取值,纵坐标代表PR@K值的水平。在实验的时候,把原来异常检测模块的差值法去掉,调整核密度的超参数。已知阈值取值在[0,1]范围,值越大,则对异常越灵敏,检测的异常越多。对于PR@1,横坐标阈值越大,对应的纵坐标性能值有逐渐减小的趋势。这是因为随着异常检测越来越灵敏,出现假阳性的概率也越大,从而会影响最后异常评分的排名。对于PR@3,虽然阈值变大,异常检测越来越灵敏,但性能值不会有多大的变化。这是因为真正的异常指标不会被漏检,在构造异常子图权重和偏好向量时不会有太大的改变,因此,最后评分的排名也不会有过大的变动。

图7 核密度估计方法调节阈值后,PR@K值的表现
差值法受控于式(4)中的调节因子。调节因子是一个大于0的正数,值越小则对异常越灵敏。图8给出了在调节因子分别为1,2,3,4,5的条件下性能的情况。如图8所示,调节因子对结果无影响。这是因为该异常检测方法能检测到所有由根因故障引起的异常指标,当调节因子变大时,虽然异常指标变少了,但是基于PageRank的随机游走算法还是能够正常推断出根因。

图8 差值法调节因子后,PR@K值的表现
4 结语
本文提出了一种基于调用链时序分解的微服务根因定位方法StudRank。该方法首先通过计算调用节点的时延性能,把调用链数据转化为多个时序数据;其次基于指标异常检测,构造异常子图;最后基于PageRank的随机游走算法,对节点根因定位。基于公开数据集对所提方法进行实验,结果表明,所提方法的PR@1指标达到了84%,并与微服务根因分析经典方法进行了对比,较其中效果最好的MicroRCA指标提升了97.6%。然而,如果存在某一种类型的调用链,其历史数据比较少,或者访问的频次小,出现故障时,很可能这类故障会被漏检。此时,如果分析每个调用链,又会造成计算效率低下的问题。因此,如何高效且细粒度地分析调用链,是未来需要进一步研究的方向。
