一种分布式无线网络自适应拓扑抗毁性优化机制*

毛建兵，邓伟华

（中国电子科技集团公司第三十研究所，四川 成都 610041）

0 引言

在Ad hoc分布式无线网络中，网络可靠连通是发挥网络效能的重要基础[1]，拓扑控制是增强网络连通性和抗毁性的重要手段[2]。通常对网络采取拓扑控制决策，需要首先获取网络当前的拓扑状态信息。对于较大规模的网络而言，获取全网拓扑信息需要网络节点之间进行大量的控制信令交互，这些交互将为网络带来大量的通信开销，甚至产生“信令风暴”这一不良影响，加重网络负担[3]。因此，为了弥补全网拓扑信息获取的不足，基于局部网络拓扑信息实现分布式网络自适应拓扑控制优化的方法被提出，这是网络抗毁性增强研究的一个重要方向。

分布式网络的拓扑结构影响着网络的通信性能和抗毁性能[4]。基于分布式网络的多智能体系统应用中，一致性协议的收敛速率跟网络拓扑密切相关。相关研究表明，一阶多智能体系统在渐进收敛的一致性协议驱动下，系统的收敛速度由分布式网络拓扑的代数连通度所决定。网络拓扑的代数连通度越大，其一致性协议的收敛速率越高[5]。

在网络抗毁性研究方面，基于代数连通度的方法从图的频谱角度进行拓扑结构的抽象分析[6]。网络拓扑的代数连通度越大，直接反映出网络的抗毁性和鲁棒性越好[7]。代数连通度分析在各类网络的设计与研究中都扮演着重要的角色[7-8]。

为获得代数连通度最大的网络拓扑，相关研究将拓扑优化问题建模为数学优化问题，并利用优化算法进行求解。但最大化代数连通度的优化问题并不是一个严格凸的规划问题，而已被证明是一个NP难问题[5]。不仅如此，一般网络拓扑的优化问题通常也同样是一个NP难问题[9]。因此，启发式算法被设计用于提高网络的代数连通度，从而得到较优的网络拓扑。

针对分布式无线网络，本文研究提出了一种自适应网络拓扑抗毁性优化机制，并设计了分布式启发式算法。通过利用代数连通度计算对节点k跳邻域范围内的网络拓扑结构进行分析，选取其中的冗余节点，然后对冗余节点进行局部移动，调整优化网络拓扑结构，实现网络整体代数连通的提升，增强网络抗毁性能力。仿真分析结果表明，所提算法能够显著有效改善网络的连通性和抗毁性，大幅提升网络的代数连通度。

1 网络模型及相关定义

1.1 网络模型

考虑无线网络由N个节点构成，N个节点根据应用或任务需要，部署工作在一定区域范围内，形成一个多跳的无线自组织网络。非邻居节点可通过其他节点提供的路由中继服务实现多跳连通。网络中节点可根据需要移动，并改变网络的拓扑形态。网络中节点通过路由协议的拓扑学习功能，可以掌握邻近k跳范围内节点之间的连接信息，获得k跳邻域网络拓扑。

为了描述方便，本文以图论模型的无向图G=(V,E)来表示网络拓扑，其中，V为网络中的节点集合，E为网络中节点之间的链路集合。如果网络中两个节点vi，vj可以直接通信，则两个节点之间存在一条链路e(vi,vj)∈E。拓扑图G中节点的度定义为节点连接的链路数目。网络中两个节点vi，vj之间的跳数定义为连接vi和vj路径的最小链路数。

1.2 代数连通度

设A(G)是网络拓扑图G的邻接矩阵表示，其表达式为：

式中：矩阵元素aij=1表示节点vi,vj之间存在链路；否则，aij=0。特别地，aii=0。

以D(G)表示图G各节点的度所构成的对角矩阵，则有：

以L(G)表示图G的拉普拉斯矩阵（Laplacian matrix），其计算表示为：

拉普拉斯矩阵L(G)是一个实对称矩阵，其特征值均为非负实数，最小的特征值是0，全部N个特征值经排序后可以表示为0=λ1≤λ2≤…≤λN。图G的代数连通度表示为λ(G)，其值为矩阵L(G)的第二小特征值，即有：

相关研究指出[5-6]，网络拓扑图的代数连通度越大，表明网络的连通性越好，网络拓扑具有更好的鲁棒性和抗毁性。

2 优化机制与算法设计

2.1 主要思路

对于大规模网络而言，获取全网拓扑信息往往存在一定困难，同时网络节点数量越多，计算网络拓扑图矩阵信息及拓扑优化调整的维度也越大，因此优化过程的计算复杂度非常高，难以求得优化解。在此条件下，为了增强网络的抗毁性能，提高整体网络拓扑的代数连通度，引入启发式算法实现网络中节点分布式自适应地拓扑优化调整。本文研究的启发式算法设计，从评估节点邻近k跳范围的网络拓扑出发，选取对局部网络拓扑连通性影响最小的冗余节点，小范围内调整优化这类节点的位置部署，以提高局部k跳邻域范围内的网络拓扑代数连通度。通过网络中各个节点分布式自适应优化动作，提升各所在局部邻域网络拓扑的代数连通度，并经过多次迭代优化，最终实现网络整体代数连通度和抗毁性能的总体提升。

2.2 冗余节点分析

定义冗余节点为k跳邻域范围内网络拓扑删除该节点后对代数连通度下降影响最小的节点。以Gi表示节点i获取的k跳邻域范围内网络拓扑图，Gi´表示图Gi删除节点i及与节点i相关的连接边后的子图。分别计算Gi和Gi´的代数连通度，对应表示为λ(Gi)和λ(Gi´)。计算节点i删除后代数连通度变化的归一化值ηi：

式（5）中，由于λ(Gi´)≥0，有ηi≤1。

节点计算ηi后，将结果ηi在k跳邻域范围内进行通告，同时也收集其他节点通告的计算结果。设节点i在k跳邻域范围内共有Ni个节点，相应代数连通度变化的归一化值计算表示为ηj，1≤j≤Ni。节点i通过比较ηj，确定k跳邻域范围内的冗余节点。若邻域节点m满足：

则节点m即为节点i在k跳邻域范围内的一个冗余节点。为了使得拓扑优化在达到一定条件时消除冗余节点，并且算法终止，这里设置阈值参数α，要求冗余节点满足ηm≤α。

在评估网络拓扑过程中，k取值越大，获取的邻域范围内网络拓扑信息越多，则对冗余节点的判定就越准确。通常网络条件下，设置k=2。特别说明，如果节点i是一个割点，删除节点i后，网络拓扑不连通，代数连通度计算有λ(Gi´)=0，相应有ηi=1。割点是拓扑连通的关键节点，不能被选为冗余节点，因此ηi=1的节点不能判定为冗余节点。除去特殊的链状网络拓扑结构，节点k跳邻域范围内ηj(1≤j≤Ni)的最小值ηm通常有ηm＜1。

图1给出了一种邻域网络拓扑，通过对网络拓扑进行冗余节点分析，节点1成为邻域范围内的冗余节点。

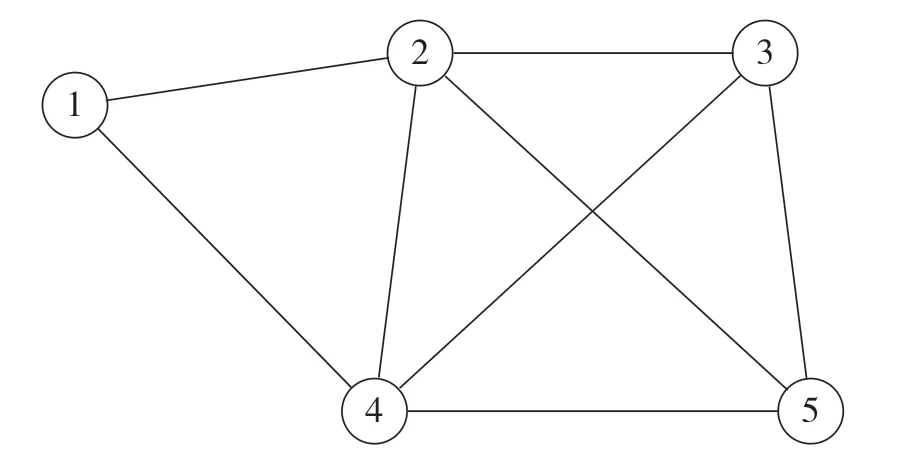
图1 邻域网络拓扑

2.3 拓扑优化策略

冗余节点移动部署的目的在于提升k跳邻域范围网络拓扑的代数连通度。因此，所针对的目标节点应该是k跳邻域范围内网络拓扑代数连通度较小的节点。本文算法按k跳邻域范围内节点代数连通度λ(Gi)进行排序，从λ(Gi)最小的节点开始选取为目标节点Obji执行拓扑优化操作。

一个节点k跳邻域范围内拓扑代数连通度较小，说明节点的k跳邻居之间的相互连接不够紧密。利用冗余节点进行拓扑优化的目的是尽可能地强化邻居节点之间的连接关系。同时，还需要兼顾冗余节点只在邻近范围内近距离移动，避免远距离、大范围的移动影响节点执行应用任务。

对于目标节点Obji，如何通过冗余节点Rx移动增加其邻域范围内的连接，使得目标节点拓扑的代数连通度得到最大的改善，是优化设计需要追求的目标。相关研究指出，通过向给定图中添加边来最大化代数连通度是一个困难的组合问题，其难以求得确定的最优解[5]。

受文献[10]研究的启发，连接拓扑图中最小度节点与边距离（最短路径上包含的边数）最大的节点可以较大程度上提高代数连通度的大小。本文算法设计连接目标节点Obji的k跳邻域范围内的最小度节点Vd，以及最小度节点k跳范围内跳数h最大并且欧式距离d最近的节点Vh。为了限制冗余节点的移动范围，约束在冗余节点Rx的k跳邻域范围内搜寻目标节点Obji邻域的最小度节点Vd，并且距离d要求不超过节点通信半径r的2倍。为了连接节点Vd和Vh，冗余节点Rx需要向节点Vd和Vh的中间位置进行移动部署。针对特殊通信环境，也可以利用无线传播模型进行链路预测分析，寻找最佳的移动部署位置。

2.4 算法工作流程

网络中一个节点可能被多个邻居节点选取为冗余节点。定义节点i的冗余权重参数wi为节点被k跳邻域范围内邻居节点选中为冗余节点的重数。权重参数wi越大，表明冗余节点在k跳邻域范围内对邻居节点拓扑的影响越小。因此，在拓扑优化过程中，算法将优先对权重更高的冗余节点进行优化移动。

算法设计主要工作流程如下：

（1）节点i采集k跳邻域范围内的局部网络拓扑信息，计算邻域拓扑图Gi，生成邻接矩阵A(Gi)，并计算代数连通度λ(Gi)。

（2）计算节点i删除后代数连通度变化的归一化值ηi，并向k跳邻域内节点进行通告。节点i同时也收集邻域内其他节点通告的信息。

（3）节点i选取k跳邻域范围内ηm=min{ηj,1≤j≤Ni}且ηm≤α的节点m为冗余节点，并向邻域内节点进行通告。

（4）节点计算冗余权重参数wi，并在邻域内进行通告。k跳邻域范围内，权重参数wi最大的冗余节点Rx优先调度用于执行拓扑优化。

（5）冗余节点Rx选取k跳邻域范围内代数连通度λ(Gi)最小的节点为优化目标节点Obji。

（6）在目标节点Obji与冗余节点Rx共同的k跳邻域范围内搜寻最小度节点Vd，以及最小度节点k跳范围内跳数h最大并且欧式距离d最近的节点Vh。

（7）根据链路预测分析，将冗余节点Rx向连接节点Vd和Vh的最佳位置进行移动部署。

（8）重复上述算法步骤，直至所有冗余节点完成自适应优化移动部署，网络中不再存在冗余节点，或者冗余节点对目标节点Obji代数连通度λ(Gi)的优化提升小于预期目标。

3 仿真分析

通过软件模拟，对提出的拓扑抗毁性优化机制进行了仿真。默认情况下，设置节点通信半径r=5 km，参数α=0.1。为了比较直观地显示拓扑优化带来的效果，首先针对图2（a）所示的一个小型网络拓扑进行仿真试验。仿真网络拓扑图中节点以圆圈表示，虚线表示节点间链路，数字标注表示节点的编号。优化前网络拓扑的代数连通度为λ(G)=0.538 6；执行算法优化，网络拓扑调整后的结构状态如图2（b），其中代数连通度为λ(G)=0.982 5。可见，网络拓扑的代数连通度得到了大幅度提升，提升幅度达到82.4%。直观来看，优化后的网络拓扑中节点6的邻居节点之间的连接更为紧密了，其割点身份消除了，并且优化后的网络拓扑中也不再存在割点。

图2 网络拓扑示例（N=9）

进一步地，将拓扑优化算法应用于更复杂的大规模网络。设置网络分布场景大小为20 km×20 km，N=50个节点以均匀概率随机部署在场景内，生成的网络拓扑如图3所示。

对图3所示随机网络拓扑进行了k跳邻域范围内局部拓扑代数连通度的计算分析，其结果如图4所示。同时，对全网拓扑的代数连通度进行计算，结果有λ(G)=0.196 2。对比结果可以看出，当k=2时，邻域范围内拓扑的代数连通度λ(Gi)最小值已经很接近全网拓扑的代数连通度λ(G)计算结果。因此，通过拓扑优化提升k=2跳邻域范围内的λ(Gi)最小值，可以达到间接提升全网拓扑的λ(G)的目的。

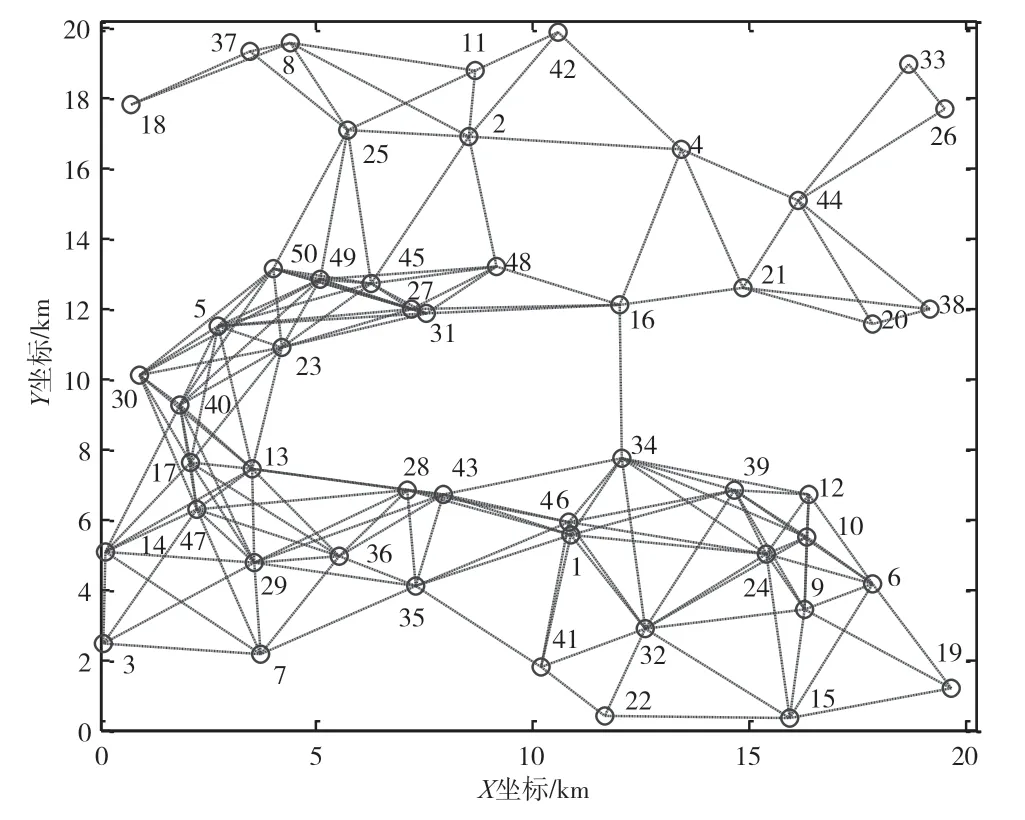
图3 网络拓扑示例（N=50）

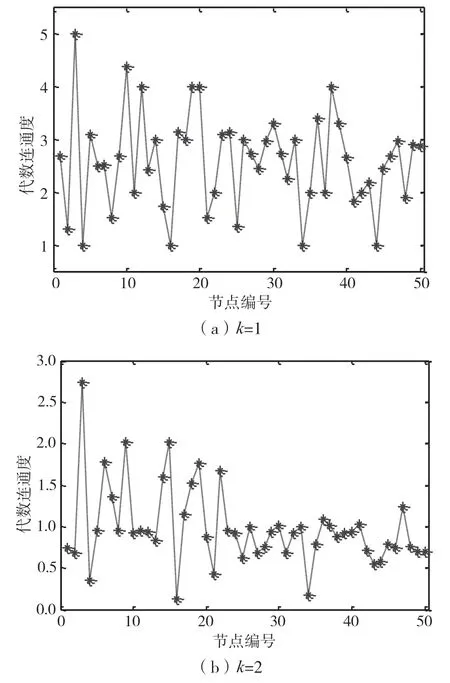
图4 k跳邻域范围拓扑代数连通度计算

图5给出了通过算法冗余节点分析得到的全网各个节点的冗余权重参数wi结果，其中wi=0表明节点非冗余节点。可以看到，全网仅少部分节点被选取为冗余节点。全网有N=50个节点，冗余节点仅选出其中7个节点，不到全网节点数的15%。执行拓扑优化的冗余节点数较少，避免了算法执行中大量网络节点移动部署产生的较高代价，减小了对网络节点应用任务的影响。

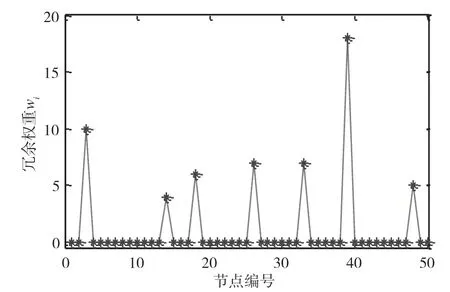
图5 节点冗余权重wi的计算结果

图6给出了图3所示随机网络拓扑执行拓扑优化后的最终网络拓扑结构状态。可以看出，优化后的网络拓扑节点之间连接更为紧密，能够更好地应对部分节点损毁导致的拓扑连接中断或是分裂。

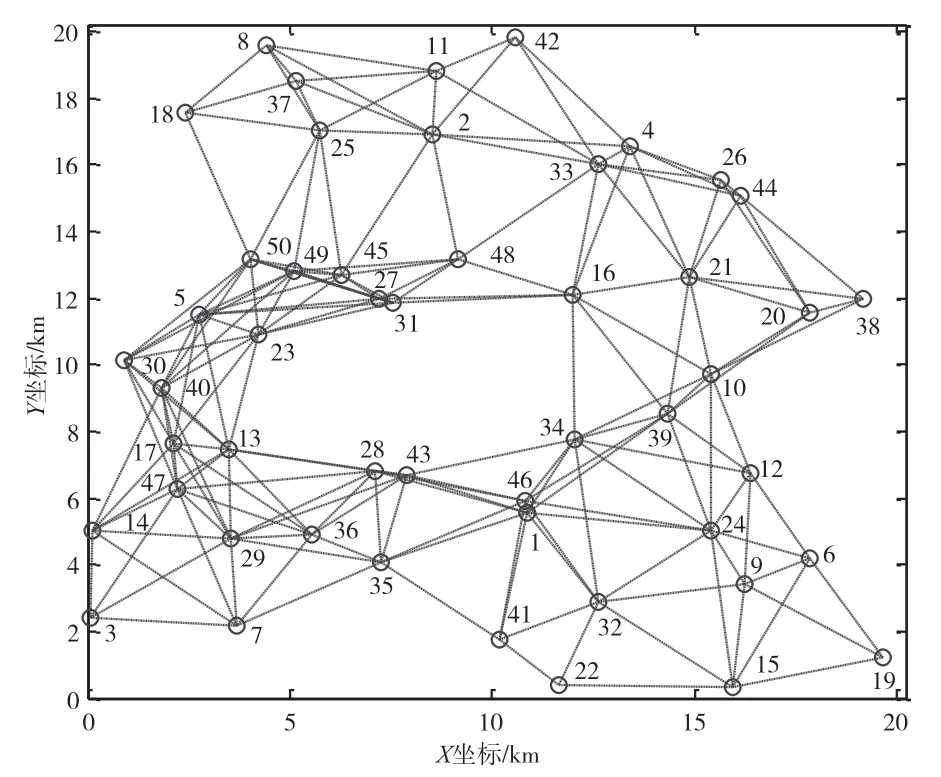
图6 优化后网络拓扑（N=50）

针对图3所示网络拓扑的优化结果，图7给出了算法迭代运行过程中全网拓扑代数连通度λ(G)的结果变化。经过算法的多次迭代，最终网络拓扑的代数连通度提升到了λ(G)=0.502 6，与初始网络拓扑的代数连通度λ(G)=0.196 2相比，提升幅度达到了156.2%。可见，所提算法对网络拓扑的抗毁性优化效果显著，并且优化过程仅需较少的迭代次数。

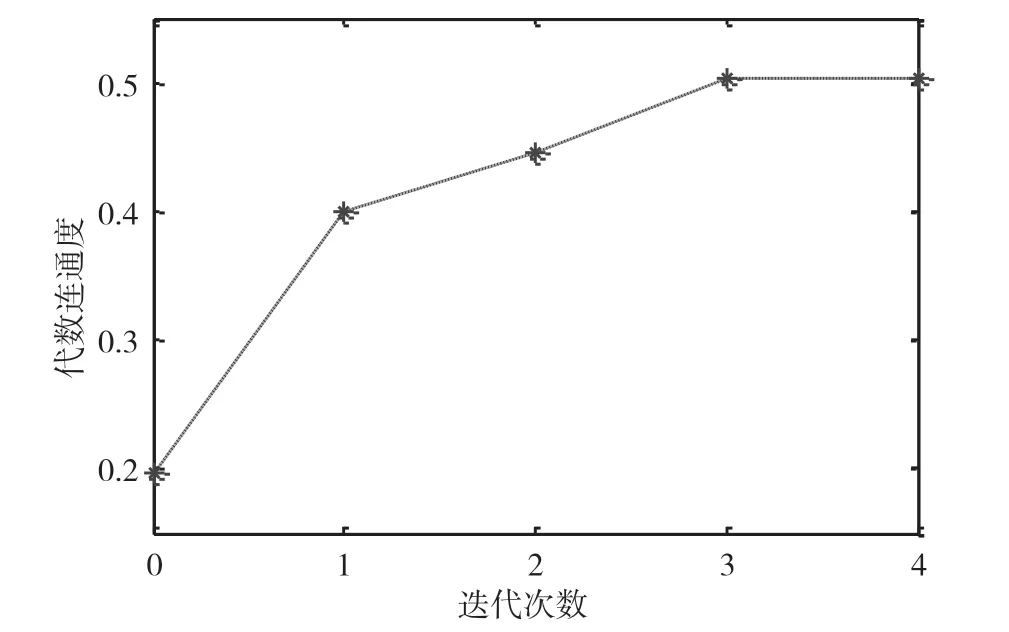
图7 算法多次迭代过程中全网λ(G)变化

4 结语

拓扑优化控制能够使得分布式无线网络的连通性和抗毁性得到显著改善，并维持在一个较高的水平。对于拓扑不断变化的网络而言，根据实时网络拓扑分析进行自适应优化控制显得非常必要。针对获取全网拓扑信息受限的大规模网络，本文提出了一种基于邻域网络拓扑信息的自适应抗毁性优化机制，并设计了启发式算法。通过算法的迭代运行，自适应选取网络中的冗余节点，并将冗余节点在小范围内局部移动，使得网络拓扑结构的连通性和抗毁性得到改善。仿真实验结果表明，所提算法能够有效提升整体网络的代数连通度和抗毁性。