Perspectives on the flexibility analysis for continuous pharmaceutical manufacturing processes

Wenhui Yang,Wuxi Qian,Zhihong Yuan,,Bingzhen Chen

1 State Key Laboratory of Chemical Engineering,Department of Chemical Engineering,Tsinghua University,Beijing 100084,China

2 Department of Chemical Engineering,Tsinghua University,Beijing 100084,China

Keywords:Pharmaceuticals Model Optimization Continuous manufacturing Flexibility Uncertainty

ABSTRACT Pharmaceutical continuous manufacturing,especially under the context of COVID-19 pandemic,is regarded as an emerging technology that can guarantee the adequate quality assurance and mitigate process risk while guaranteeing the desirable economic performance.Flexibility analysis is one approach to quantitively assess the capability of chemical process to guarantee feasible operation in face of variations on uncertain parameters.The aim of this paper is to provide the perspectives on the flexibility analysis for continuous pharmaceutical manufacturing processes.State-of-the-art and progress in the flexibility analysis for chemical processes including concept evolution,mathematical model formulations,solution strategies,and applications are systematically overviewed.Recent achievements on the flexibility/feasibility analysis of the downstream dosage form manufacturing process are also touched upon.Further challenges and developments in the field of flexibility analysis for novel continuous manufacturing processes of active pharmaceutical ingredients along with the integrated continuous manufacturing processes are identified.

1.Introduction

The global and intensive marketplace has become more and more liberalized,exposing products to higher and higher competitive pressure,particularly in the scope of the fine chemicals [1].Product developments,manufacturing strategies,and management technologies require transformative innovation.During the last decades,a shift has been under way in the pharmaceutical manufacturing sector that continuous manufacturing mode trends to be more and more appealing to both academia and industry.Generally speaking,economic and regulatory aspects are two main driving forces of this trend.As is shown in Fig.1,the global spending on medicines had reached 1.27 trillion USD in 2020 [2],and such value is expected to exceed 1.6 trillion USD by 2025 [3].Clearly,Fig.2 indicates that,the market in developed countries is close to saturation while the developing countries is the backbone of the development of the pharmaceutical industry.The growth of the world population,and the improvement of social aging,as well as the outbreak of COVID-19 epidemic have cultivated the growing awareness on health care.

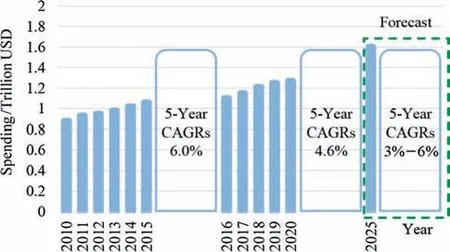
Fig.1.The global pharmaceuticals spending and growth,2010–2025.

For the purpose of tailoring to the diversification and integration of patients’needs,pharmaceutical innovation and modernization should get sufficient support from governmental regulations.Indeed,the regulatory agencies across the world,such as U.S.Food and Drug Administration (FDA),European Medicines Agency(EMA),and National Medical Products Administration (NMPA,China),have different perspectives with respect to the pharmaceutical development and innovation.However,they arrived at a consensus at the Quality by Design(QbD)paradigm introduced by ICH guidance Q8(R2),Q9,and Q10[4].These authoritative documents originally provide high-level guidance on the scope and definition of QbD in the field of pharmaceutical industry [5,6].Based on the mechanistic models and Design of Experiments (DoE),QbD is an effective approach to addressing the product and process understanding for systematic design and operating space.As illustrated by Fig.3,with the development of pharmaceutical manufacturing mode,the advancement of QbD has been extensively highlighted and enriched recently as advanced process control has been introduced.Consequently,a new concept named Quality by Control(QbC) has been formulated [7].More specifically,QbC leverages the quantitative and predictive understanding for integrated active control with robust process design and optimization.Clearly,QbC paradigm in the foreseeable future will in turn lay the foundation of the next generation of continuous smart manufacturing of pharmaceuticals[8,9].From the viewpoint of process systems engineering (PSE),the robust control performance is heavily dependent of process operability properties including controllability,stability,and flexibility.

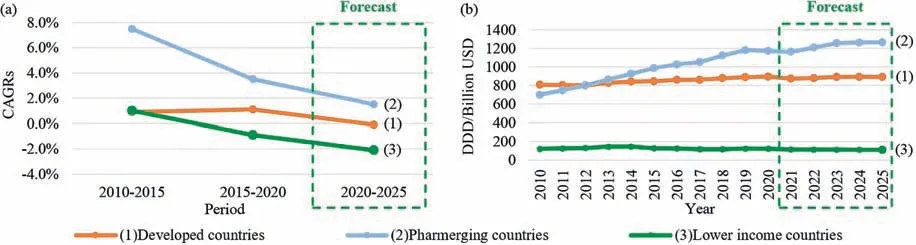
Fig.2.(a) Pharmaceuticals defined daily dose (DDD) share and (b) Pharmaceuticals DDD growth in different countries,2010–2025.

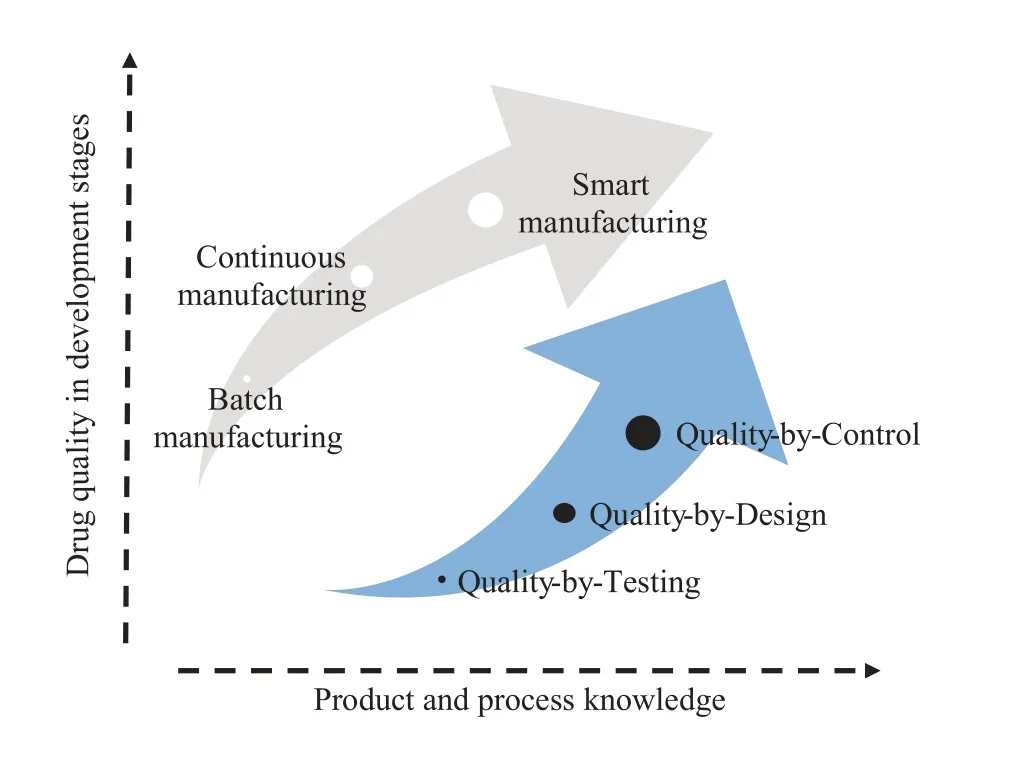
Fig.3.The systematic progression in quality assurance via Quality by Testing(QbT),QbD and QbC [8,10].

In order to further promote and foster the development of QbD and QbC,the scope of this paper is to emphasize the importance and urgency of flexibility analysis for continuous pharmaceutical manufacturing (CPM) processes.Although the development of CPM process is still at its early stage,and the relevant flexibility analysis is very rare,the simultaneous considerations of process design and process operability analysis do guarantee the operation performance and drug quality for the pharmaceutical manufacturing processes.Needless to say,the economic performance can be significantly enhanced.

The paper is organized as follows.Section 2 briefly compares the traditional batch and CPM.Section 3 provides the descriptions on fundamental concepts and mathematical formulations for flexibility analysis.Section 4 historically overviews the evolution of flexibility analysis.Section 5 presents the results of the preliminary applications of flexibility analysis for CPM.Section 6 indicates the future directions.Finally,concluding remarks are drawn in Section 7.

2.Batch Manufacturing vs.Continuous Manufacturing

Batch production mode has traditionally dominated in the pharmaceutical industry during the past several decades.One major advantage of batch process is,exactly,the flexible operation.Theoretically,different production targets are able to be adjusted between batches flexibly,which means a set of equipment(stirred tank reactors,batch filters,centrifuges,and dryers)can fulfill more than one purpose [11].However,its disadvantages have gradually emerged as poor process understanding,yield,storage volume utilization,scalability,and heat and mass transfer [12].More importantly,the batch manufacturing mode may have some difficulties in manufacturing a stable product quality,especially the high added-value products.The shift from the conventional batch manufacturing to the continuous manufacturing method -eliminating the batch process drawbacks -is gaining momentum nowadays[13–15].Fig.4 illustrates the transformation from batch production mode to its continuous production counterpart based on the microchemical technologies and flow chemistry approaches.However,the main barrier of flow chemistry driven CPM is how to effectively address the high-viscosity and solid flows [16].On the other hand,the control and monitoring technology are in their extremely early stage.

FDA and EMA commission have set their distinct pharmaceutical development strategies.They,however,believe that adopting continuous manufacturing for pharmaceutical production will address the drug product quality issue,lower manufacturing costs,and improve availability of quality medicines to patients.Specifically,the advantages of CPM include an increase in efficiency of productivity and economy;maximized automation by the unit operations interconnection;enhanced product quality,robustness,and safety via continual automated monitoring of process;shortened overall process and system development time as scaling-up replaced by numbering-up;reduced waste and energy under the restrictive environmental legislation [11,17,18].CPM exactly has the power to implement changes in technology beyond preset corridor of batch process.SRI International has already conducted extensive experiments focusing on the continuous ibuprofen manufacturing,and the overall conversion rate can reach as high as 82%without much waste or heavy and expensive catalyst [19].Corporations have been motivated by these potential profits which is the driven force for the development of CPM.Additionally,the Eli Lilly,the Medicines for All Institute (M4ALL),and the GlaxoSmithKline have started to examine the benefits of continuous manufacturing for pharmaceuticals [20].

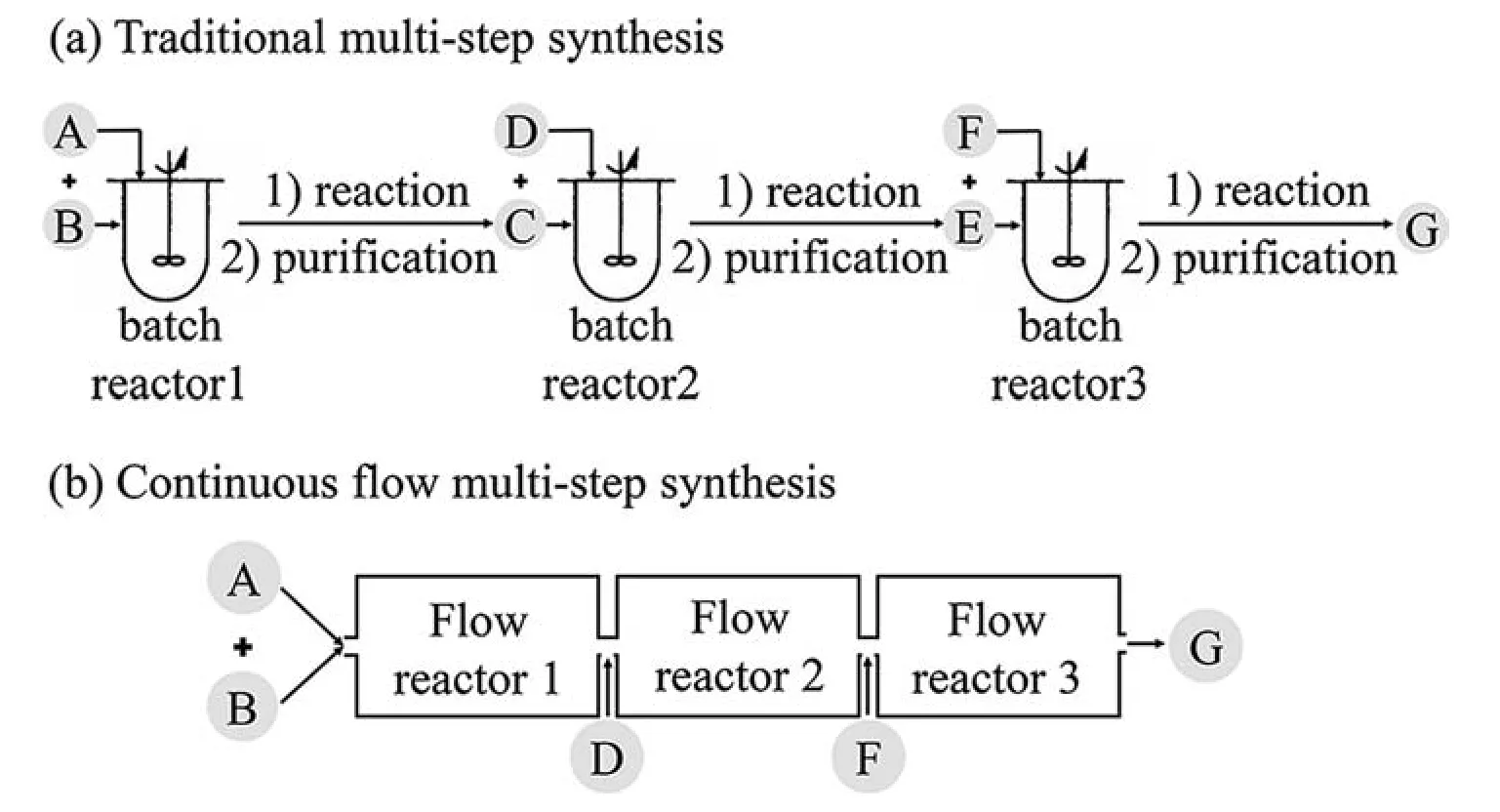
Fig.4.Batch process vs.continuous manufacturing [13].

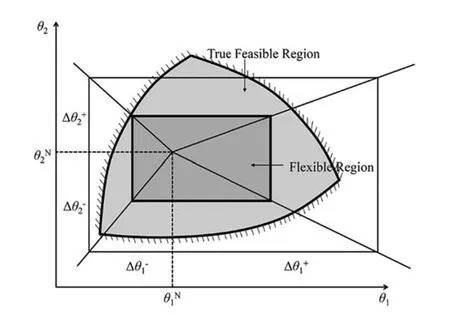
Fig.5.Feasible region and flexible region.

3.Fundamental Concepts and Mathematical Formulations for Flexibility Analysis

The lessons from the flexibility analysis of continuous pharmaceuticals process exhibited that the desirable flexibility properties and the overall economic performance are in tension [21].On the other hand,during the new drug and manufacturing process research and development stages,various uncertainties may occur sometimes.These uncertainties may seriously influence the feasibility of the design on operation strategies.In other words,the trade-off between the feasibility issue and overall economic perform including research and development costs should be clarified.

3.1.Concept definitions

Flexibility:the ability of a chemical process or pharmaceutical manufacturing process to maintain feasibility operation over a range of uncertainty or changing conditions such as the flowrate/temperature variables and stream quality fluctuations.Before delving into the following sections,some confusing terminologies in the discussion of flexibility are firstly clarified [22].

(I)Flexibility and operability.As is defined by Swaney and Grossmann,operability considerations involve four characteristics -flexibility,controllability,reliability,and safety[21].However,another break-down of operability consists of stability,optimality,measurements,manipulated variables,flexibility,and controllability [23].One of what they share in common is that flexibility is an important constituent property of operability.It follows that flexibility isn’t concern of any control structure or control effect but exclusively focuses on the relationship between input variables and the presence of uncertainties [24].

(II)Flexibility and resiliency.Resiliency emerges from the heat exchanger networks(HEN)to quantify the ability of recovering from misfortune or change of input and target temperature[25–27].Flexibility defines the ready ability to adapt to the requirements of changing conditions in the steady state,while resilience emphasizes the dynamic power of recovery or adjustment after strain fast and smoothly.Grossmann and Morari provided a thorough understanding of flexibility and resilience by quantitative articulation which indicates that these two properties are not much for a difference [28].In brief,static resiliency equals to flexibility to some degree[29].

(III)Flexibility and feasibility.These are two concepts of great similarities.Things will go very puzzled as we only consider to their positive forms.In contrast,if the corresponding antonyms are compared together,the answer will stand more clearly and vividly.According to Merriam Webster,inflexible means incapable of change,whereas infeasible indicates incapable of being used or dealt with successfully.The validity of this idea can be incarnated in some serialized articles [30,31].

(IV)Feasible region and flexible region.Feasible region is also a fuzzy definition in the context of flexibility.As illustrated by Fig.5,the feasible region,in general,means the feasible region bounded by all the inequality constrains (the light grey region)and the flexible region means the feasible range of operation (the dark grey region) [32].Generally,flexible region obtained by flexibility analysis is hyperrectangle with the underlying assumption that all the uncertain parameters are independent.

3.2.Classification of flexibility analysis

In a broad sense,the flexibility analysis problem can be divided into three categories.

(I) A feasibility test problem that checks whether the fixed design is able to satisfy all the constraints under the given uncertainty set.

(II) A flexibility index problem,in other words namely a flexibility assessment problem.It calculates the maximal size of the flexible region in the fixed design without moving away from the nominal point.

(III) An optimal design problem,that intends to figure out the best profitable design as an expected flexible region being a constraint [33,34].

3.3.Generic mathematical model formulations

Formulating the optimization model for flexibility analysis involves the following variables and parameters:d is design variables;x is state variables;z is control variables;θ is uncertain parameters;θNis nominal point inside the feasible region;θL,θUare lower bound and upper bound of uncertain parameters;Δθ-,Δθ+are expected deviation of uncertain parameters;T is specified parameter range;δ is flexibility index;u is auxiliary variable.

The equality and inequality constraints are involved as follows:

The equality constraints allow elimination of the state variables:

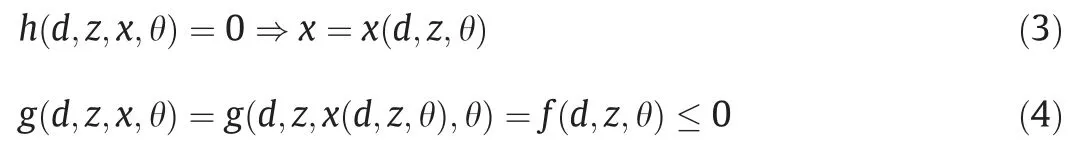
Feasibility test problem.The max–min-max trilevel optimization problem χ（d ）presents a feasibility measurement [35]:

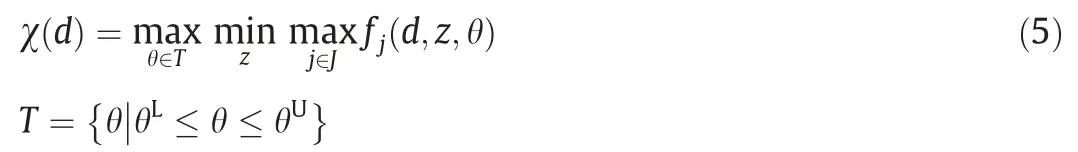
If χ（d ）≤0,the design is feasible for all the uncertainty range,whereas if χ（d ）＞0,there is at least one point in the set θ ∈T violates the constraints.By incorporating ψ（d，θ）into the above nondifferentiable formulation,it can be rewritten as a two-level optimization problem [35]:

Flexibility index problem.The definition of flexibility index is proposed by Swaney and Grossmann as follows [21]:

It may be confusing here.In the available literatures,formulations of flexibility index,in some cases,are maximum optimization problems.And in others,they are minimum showing as bellow.

It could be summarized here that these two formulations Eq.(7)and Eq.(8)are essentially the same.In the geometric sense,Eq.(7)intends to find the maximal hypervolume inside the feasible region.While Eq.(8) intends to find the minimal hypervolume on the boundary.Fig.6 (a) and (b) intuitively show the geometric meaning.The dotted boundaries indicate the searching areas and the red boundaries are the optimal solutions found.

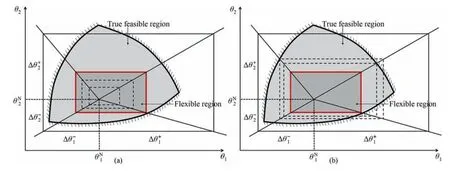
Fig.6.(a) The geometric sense of Eq.(7) and (b) the geometric sense of Eq.(8).

With the introduction of ψ（d，θ）,the two-level optimization can be stated as [32]:

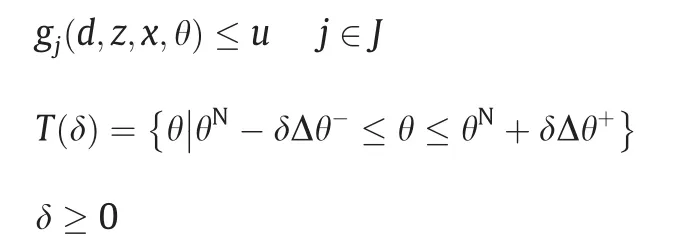
The vertex solution methods are also suggested in the convex feasible region by Haleman and Grossmann[35].Consider the vertices of the feasible region T,and let θk,k ∈V.Then,by calculating critical points on vertices,Eq.(6)and Eq.(8)can be reduced to Eq.(10) and Eq.(11).

Another important solution strategy is the application of Karush-Kuhn-Tucker (KKT) condition.By KKT,the feasibility test and flexibility index problem can be expressed explicitly in terms of a single-level mixed-integer linear programming (MILP) problem or mixed-integer nonlinear programming (MINLP) problem.Eq.(6) can be reformulated as following Eq.(12),where λjappear as the Lagrange multipliers and sjare the relative slack variables.yjare introduced as binary variables.

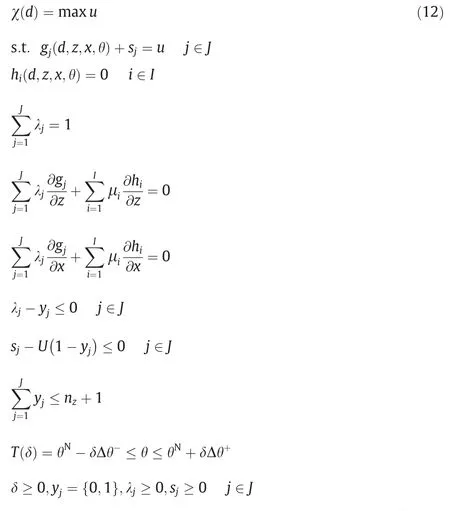
Following the same approach,Swaney and Grossmann formulated Eq.(13).Eq.(12)and Eq.(13)are essentially key observations transferring the original trilevel problems into computationally tractable formulations [21].

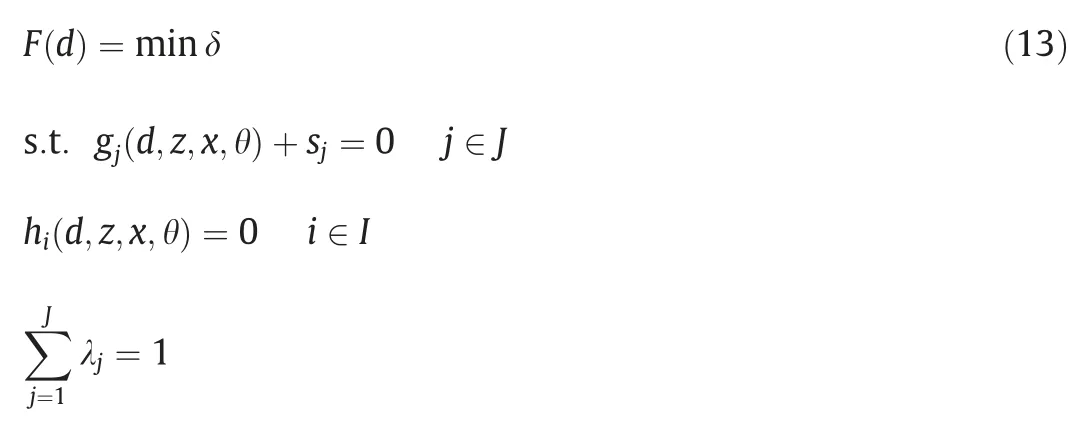
Optimal design problem.The flexibility index F is specified.In this case,the objective function of the optimal design is replaced by expected value of cost as expressed in Eq.(14) [35].With the help of ψ（d，θ）,we can comprehend this problem as searching the most economical feasible region which is able to covering completely the whole required flexible region.

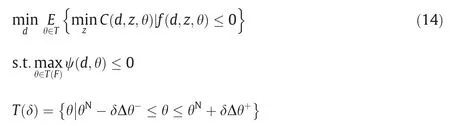
3.4.Extended forms

The traditional flexibility analysis problem has two important extended forms.On the one hand,if the uncertainties are characterized by a joint probability distribution j（θ ）,the stochastic flexibility (SF) is stated as Eq.(15) [36]:

On the other hand,dynamic flexibility problem is organized if the uncertainties are considered to be time-varying [37].The dynamic flexibility test is described as follows:for every possible uncertain θ（t）,there is at least one profile of the control vector z（t ）such that the process feasibility constraints are satisfied at any time t ∈［0，H］ [38].Accordingly,the flexibility test statement Eq.(5) is changed into Eq.(16) as shown below:

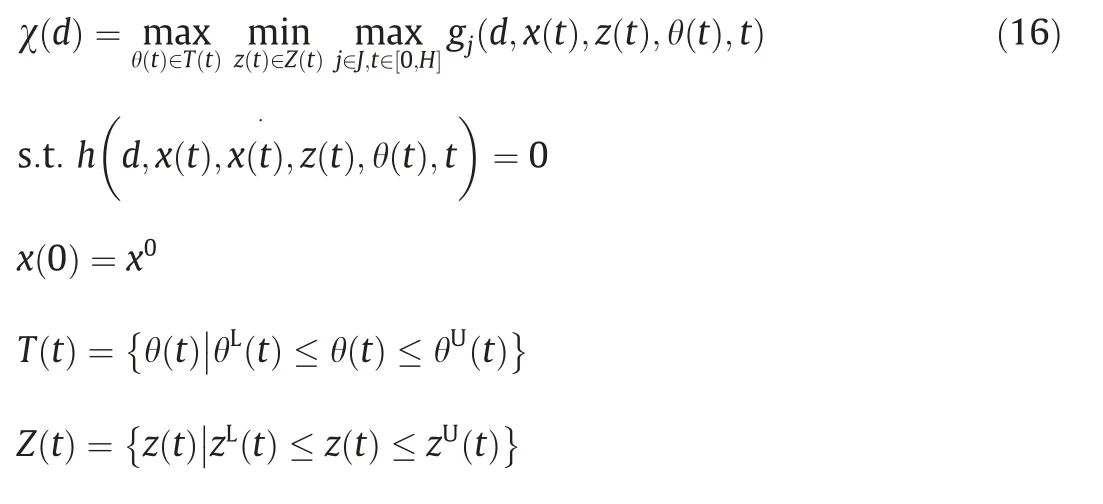
4.Overview on the Evolution of Flexibility Analysis

Recall the graphical comparison by Fig.4,the CPM technology can exhibit several advantages over the batch counterpart.The variations on inlet conditions of flowrates may affect several process units and even cause the infeasible operation.Therefore,it is of vital importance to quantitively assess the feasibility of the design space.Indeed,the application of the concept of flexibility analysis has been proven to be very important and useful in the flexible design space definition for chemical processes.

This section provides historical overviews on flexibility analysis dating back to the mid-1970s.Over the nearly 50 years,flexibility has been developed into one of relative mature branches to deal with uncertainties in the PSE community.Note that we roughly divide the evolution of flexibility analysis into three domains,concept evolution,solution innovation and application extension.

4.1.Concept and mathematical model formulation evolution

In the first twenty years,the area of flexibility analysis mainly focused on the conceptual innovation.A number of relatively new concepts were launched in this period,such as feasible test,flexibility index,trilevel or bilevel optimization,KKT utilization,stochastic flexibility and so on.The evolution process from 1975-1998 is stated and summarized in Fig.7.

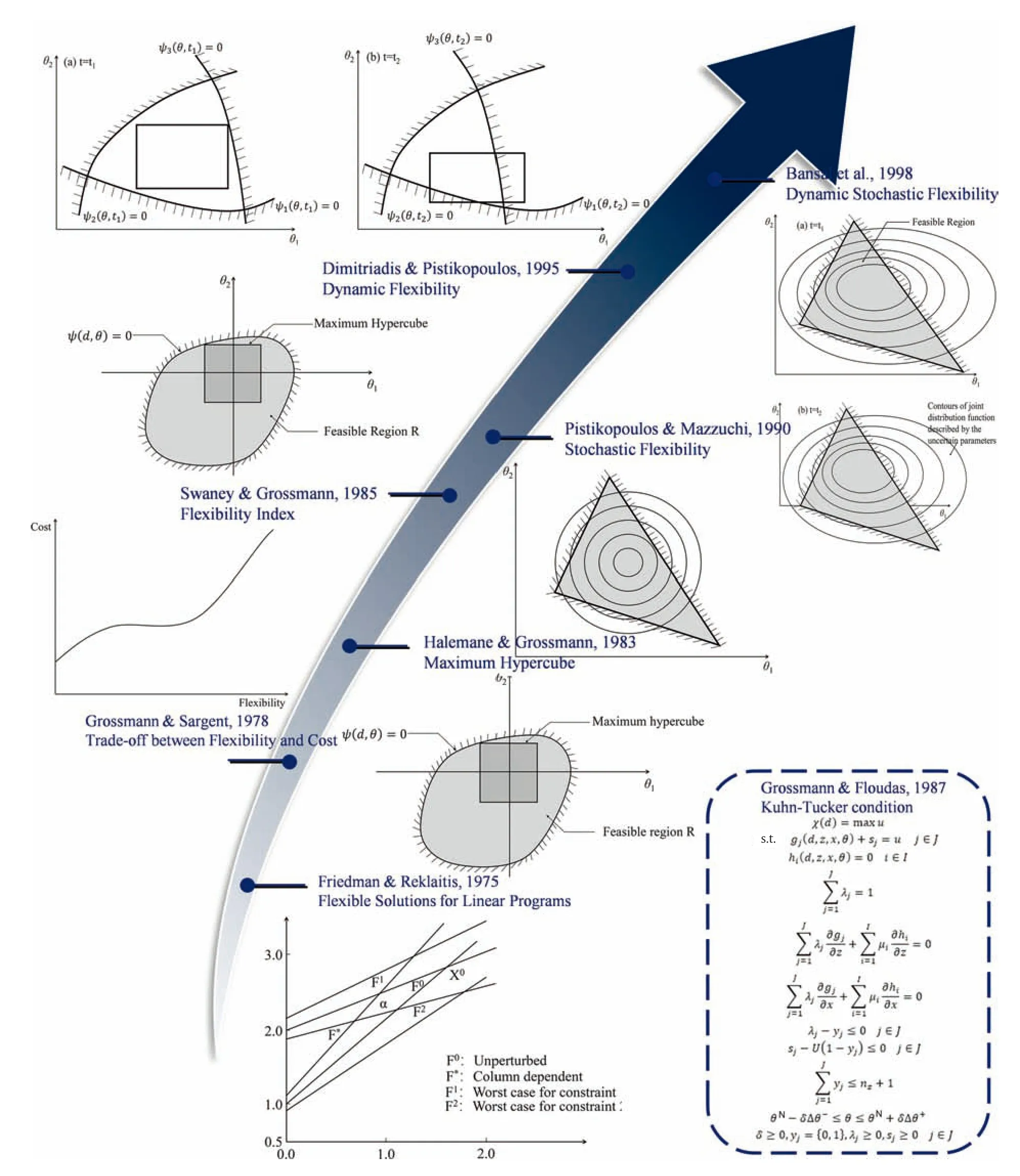
Fig.7.The evolution process of flexibility analysis from 1975-1998.

With the aim of identifying feasible region with equality or inequality constraints under a group of known variations of parameters,the seminal work by Friedman and Reklaitis formulated a linear programming model to propose the definition of flexibility set which intersects all perturbed constraint sets[39].The worst-case idea used in this model can be considered as inspiration for the following vertex solution.Three years later,Grossmann and Sargent embarked on nonlinear system,which lays the foundation for the further flexibility development.To account systematically for the uncertain parameters in both design and operation stages,two objective functions of design and economy are considered simultaneously[40].As a result,the plants are able to permanently satisfy specifications for any values of the parameters involved and,at the same time,are optimum with respect to a weighted cost function.The division of variables into design variables d and control variables z truly reflects the decision-making process of chemical plant design and operation.However,the mathematical formulation of optimal flexible chemical plants design has not been analyzed by then,until projection-restriction strategy takes the lead to tackle this deterministic multi-period nonlinear programming [41].The following works demonstrated that the projection-restriction technique can possibly further reduce the computational time by decomposition as well.

Flexibility analysis got extensive attention in the early 1980s.Note that the above proposed formulations may fail in some cases to ensure feasibility because a rigorous mathematical max–minmax constraint appears.For the purpose of circumventing the infinite dimensionality solution,a jointly convex constraints theorem is proved which successfully transformed the infinite constraints problem into a finite vertex problem [35,42].Furthermore,Grossmann et al.[43]brought up a two-stage programming formulation to compute the availability in the design stage and the operating stage separately.A flexibility index as a metric was proposed to assess the effect of design with optimal degree of flexibility with the bounded set of uncertain parameters.

Swaney and Grossmann systematically organized and summarized the concept of flexibility index[24].By analyzing the derivatives of the constraints,an alternative scheme of efficient computational algorithms instead of direct vertices search procedure was developed.It should be noted here that this alternative approach can only be used for the condition which is jointly 1-D quasi-convex in uncertain parameters θ and quasi-convex in control variables z.Therefore,another new problem that arises here is to cope with the max–min-max optimization problem without relying on the assumption of quasi-convex.Grossmann and Floudas applied the Kuhn-Tucker condition to the lower-level of the bilevel optimization problem,which is equivalent to max–minmax problem as well[44].Thus,active constraints can be identified effectively.Later on,the trade-off between cost and flexibility captured researchers’ extensive attention [45].

Pistikopoulos and Mazzuchi concentrated on the metrics for stochastic flexibility (SF) with the assumption of a linear problem and a normal distribution model for the uncertain parameters[36].Subsequently,Straub and Grossmann expanded the SF analysis to integrate two types of uncertainties together (both continuous and discrete)without any limitation of probability distribution functions [46].Note that although the abovementioned works were already discussed explicitly,they are still restricted to linear conditions.Not until a computational method based on generalized benders decomposition developed by Straub and Grossmann,has the mature framework for SF finally been cultivated.Based on the integrated analysis of economy and capability,an optimization framework is incorporated to show the trade-off between the investment cost and SF [47,48].

At the same time,practical chemical production requirements make dynamic flexibility a fertile area for researchers.In additionto the abovementioned researches on dynamic resilience [27,49],Dimitriadis and Pistikopoulos[39]extended the steady-state analysis approach to the dynamic systems.The aforementioned active constraints and orthogonal collocation techniques were introduced to make it computationally feasible.

Similarly,the optimal design under dynamic uncertainty was carried out.By integrating control structure design and stability issues successively into flexibility framework,the flexibility,controllability,and stability were synthesized systematically in a single objective design problem [50,51].Indeed,dynamic flexibility provides a window to simultaneously consider the operability analysis and process control system design[52].The extended concepts of flexible process design that incorporate controllability,reliability and stability metrics can be found elsewhere [53–56].For example,flexibility and controllability were considered in a mini-integrated plant[57],a flexible continuous process of azo pigments synthesis [58] and heat exchanger networks [59].

Note that in the traditional feasibility test and flexibility index model,the feasible region is convex and the flexible region is hyperrectangle.But in real practice,the system models may be so complex that the classic description method may lead to inaccuracy or conservatism.In the feasibility test problem,the feasible region description is meant to cover the whole feasible region as much as possible[32].In the flexibility index problem,the flexibility index should be increased as much as possible while ensuring the feasibility.Following these principles,Table 1 provides a list of descriptions of feasible/flexible region.

Table 1 Development of feasible/flexible region descriptions from 2001 to 2019

4.2.Solution strategies

As aforementioned,there are several computationally tractable forms of testing problems,index problems and design problems,such as the two-level forms and the KKT transformed single-level forms.Ostrovsky et al.[70] addressed the significance of global solution in flexibility and feasibility problem.All the local/global solution has its corresponding restrictions.Table 2 summarizes the main solution strategies for the formulated optimization models of flexibility analysis.

Table 2 The main solution strategies for feasibility/flexibility analysis

4.3.Application endeavors

The concept and solution innovation in the field of flexibility provide an avenue to extensive applications.The application valueof flexibility originated from HEN[88].Starting from 1980s,investigations on resilient/flexible HEN synthesis have never stopped[89,90].Li et al.[91] claimed that few articles concentrated on the large scale non-convex HEN,and they successfully filled this gap.Structural flexibility analysis for heat integrated distillation columns were also carried out [92,93].In Chen and Westerberg’s works,the flexibility index of the best option was improved to a great extent under the consideration of the trade-off between flexibility and utility assumption.Wagler and Douglas [94] launched their work in optimally design flexible distillation sequences.Flexibility analysis then was applied in continuous processing plants,for example,the multi-period optimization of practical refinery plant [95].Other applications include nature gas plant [96],MSF desalination plant [97],and ternary distillation [98].

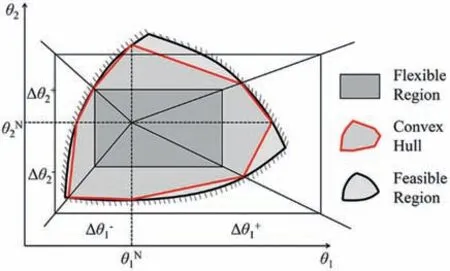
Fig.8.The feasible convex hull.

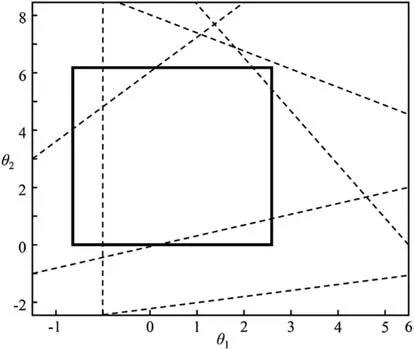
Fig.9.The flexibility region with the violation of the soft constraints [63].

5.Progress on the Flexibility Analysis for CPM Process

Section 4 clearly pointed out that the applications of flexibility analysis has been widespread in traditional chemical processes.Such fruitful researches,needless to say,will motivate the development of flexibility analysis for novel domains such as CPM.

An exciting phenome is that PSE researchers have started to put their enthusiasm to investigate the flexibility characteristics for pharmaceutical manufacturing processes.Particularly,the continuous manufacturing mode.For example,new formulations are proposed under the assumption with model parameters and process parameters,while without control variables [68,69].New solution algorithms are developed such as derivative free optimization and cylindrical algebraic decomposition [86,87].

However,there are two points to be improved in our view.One is that there are still few analysis of actual CPM process.The other is that the CPM process can be divided into two major streams:upstream and downstream section.But in general,the upstream process refers to the synthesis of the active pharmaceutical ingredients(API),while the downstream process takes the API and combines them with some excipients to create a dosage form.Based on these two points,the following progress on the flexibility analysis for CPM process are overviewed as examples.

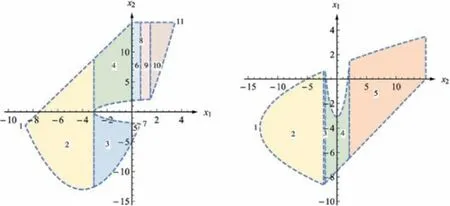
Fig.10.The flexibility region described by polynomials [65].

Fig.11.The flexibility region described by ellipsoid [67].

5.1.Flexibility analysis for ibuprofen manufacturing process

Ibuprofen is a kind of worldwide essential analgesic.Bogdan et al.[99]demonstrated that the continuous synthesis of ibuprofen affords high yield by using three plug flow reactors(PFR).Furthermore,Jolliffe and Gerogiorgis [100] did economic evaluations to a conclusion that CPM of ibuprofen promises numerous significant advantages in comparison with batch process.The process flowsheet for the CPM of ibuprofen shows as Fig.12.

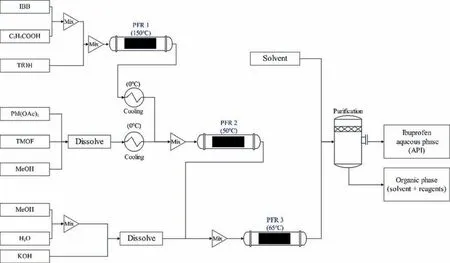
Fig.12.Process flowsheet for the CPM of ibuprofen [99].

The optimization model for the flexibility analysis of continuous ibuprofen production follows the forms of Eq.(1) and Eq.(2).The equality constraints are the material balances and energy balances.The inequalities are constrained by the heat exchangers capacity and product quality.The control variables are the feed flows of isobutyl benzene (IBB) and diacetoxyiodobenzene (PhI(OAc)2).The uncertain parameters are the feed concentrations of IBB and PhI(OAc)2and the temperatures of PFR 1 and PFR 2.Their variations are given in Table 3.

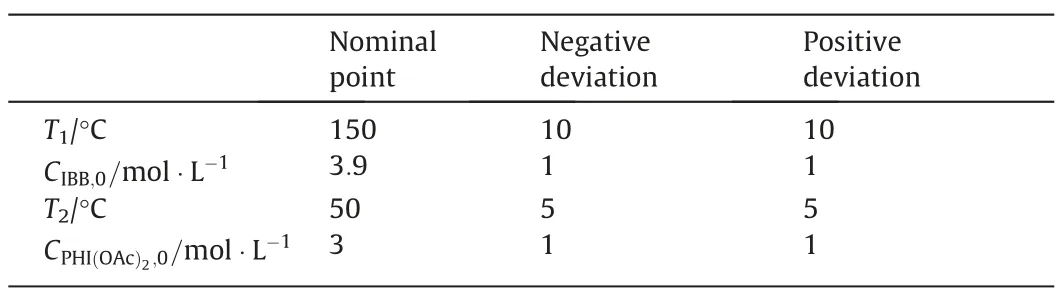
Table 3 The variations of uncertain parameters in CPM of ibuprofen

In brief,this is a flexibility analysis problem with two control variables and four uncertain parameters.Compared with the published flexibility analysis cases,the scale of this problem is relatively large.In the flexibility analysis for continuous ibuprofen manufacturing model,different combinations on control variables are investigated to reveal the benefits from taking recourse actions into account.Relations between the flexibility index and choice of control variables are discussed by several scenarios.Analyzing this model with the traditional flexibility index formulation Eq.(13)with KKT condition,we obtain the flexibility index results as 2.104 which is an appropriate result for flexibility characteristic[101].

5.2.Surrogate based flexibility analysis for downstream pharmaceutical manufacturing

Since the processing units such as reactor,crystallizer,and dryer are traditionally represented by nonlinear,nonconvex,and even disjoint equalities and inequalities,the large-scale MINLP model for feasibility and flexibility analysis may be computationally intractable.Therefore,surrogate model replacing the complex first-principles model for the feasibility and flexibility analysis of chemical processes has gained extensive attention [102].

Surrogate-based approaches for feasibility and flexibility analysis are essentially different from traditional MILP or MINLP based ones.They involve the sampling within uncertain parameter space,simulating the process model to evaluate the feasibility or flexibility function for each combination of the uncertain parameters,building a response surface for the input–output relationship,and using the response surface to identify the boundaries of the feasible region or the flexibility index.Note that the sampling step would be performed iteratively until the surrogate model is accurate enough to replace the original model.

In the downstream process,Boukouvala &Ierapetritou applied the Kriging response surface model to the feasibility analysis for a direct compaction tablet manufacturing process[84,103].Rogers&Ierapetritou[30,31]extended the Kriging-based algorithm to the feasibility analysis for the roller compaction process.Wang &Ierapetritou [104] further combined the radial basis function with adaptive sampling approach for the feasibility analysis of a roller compaction process.Boukouvala et al.[105] systematically compared the performance of different methods including response surface methodology (RSM),Kriging,and high-dimensional model representation (HDMR) or predicting the design space of continuous mixing and roller compaction processes.

6.Future Work

As aforementioned,in the past decades,the pharmaceutical industry has undergone an enormous degree of innovation and modernization to protect and promote public health.One of the main approaches for modernizing pharmaceutical manufacturing is the transition of production mode from batch to continuous.Although continuous manufacturing is not new to the pharmaceutical sector,it is still becoming increasingly more appealing to the industry and regulatory authorities.A number of enterprises,research institutes and laboratories,for example,on demand pharmaceutical (ODP),Novartis,Eli Lilly,GlaxoSmithKline,M4ALL,SRI International,Snapdragon Chemistry (a spinoff from the Massachusetts Institute of Technology),are making efforts to promote the continuous API manufacturing to come true [106].From the perspective of Industries 4.0,conducting the operability analysis of the continuous manufacturing process can provide flexible operation to allow scale-up,scale-down,capacity transition,and scaleout to accommodate changing supply demands.It can be easily checked from section 5 that the flexibility analysis for pharmaceutical manufacturing is mainly focused on the downstream tablet compaction process.The flexibility analysis for upstream API production is rare.Clearly,the feasibility and flexibility analysis still have a long way to go in the area of CPM.Following aspects needs to be tackled properly.

· Integrating flexibility analysis with stability/controllability analysis

According to ICH guideline Q8(R2),the term Quality by Design with respect to pharmaceutical industry represents a systematic approach to the development and control of drug products and their associated manufacturing processes with the sound science and quality risk management [4].A good process design for the CPM must not only take an optimal balance between capital and operating costs,but also exhibit operability characteristics that allow economic performance to be realizable under complex operating environments.As known,steady-state flexibility analysis just evaluates the capability to maintain feasible operation over a range of uncertain/random conditions.The dynamic performance is not assessed.Therefore,an optimization environment that integrates the flexibility,stability,and controllability analysis simultaneously is highly required.Correspondingly,the new quantitative measure of the flexibility and controllability should be proposed to moderate the computation burden of the resulted optimization model.

· Novel mathematical formulations for the flexibility analysis

Since the barrier of parameterizing the uncertainty set in terms of a scalar variable,the majority of the existing literatures on flexibility analysis utilize a hyperrectangle representation of the uncertainty set.The main drawbacks of the hyperrectangle representation contain the predefined upper/lower bounds for each random parameter and the lack to capture correlations between uncertain parameters.Furthermore,in some situations,the hyperrectangle representation may leads to conservative estimate.As known,promoted by flow chemistry technologies,microreactors have been introduced for the APIs production [107].If someone wants to non-conservatively evaluate the flexibility property for such processing units or systems representing by nonlinear models,how to formulate a novel and efficient but computationally tractable optimization model is of vital importance in the flexibility analysis.Needless to say,the development of multivariate Gaussian random variables and confidence regions derived from the likelihood ratio test for characterizing the uncertainty sets provides a good start point [61,66,67].On the hand,the classification of uncertain parameters such as measured/unmeasured and exogenous/endogenous should be paid sufficient attention to further reduce the conservative [68,108].

· Flexibility analysis for reconfigurable modular pharmaceutical manufacturing

With regard to the current batch pharmaceutical manufacturing mode,one challenge is that the API is often mixed with excipients and formulated in the final drug product form at a separate plant.Therefore,producingafinisheddosageformmayrequireupto atotal of one year with large inventories of intermediates at several stages.Another major challenge is drug shortage caused by variations in quality control and supply chain interruption.Continuous-flow synthesis and formulation of APIs in a modular reconfigurable manufacturing platform is an ideal approach to deal with the above issues[13,109].For example,through reconfiguring the platform,different APIs including diphenhydramine,diazepam,ibuprofen,lidocaine,atropine,fluoxetine,and doxycycline can be manufactured to respond to the real-time changes in demand or need[110].During the operations of such reconfigurable modular manufacturing platform,not only the capacity of certain products but also the structural flowsheets would change.In order to guarantee the safe and fast operations of such disruptive manufacturing platform,flexibility analysis including the operational (dynamic) flexibility and structural flexibility analysis are highly needed.

· Algorithms and strategies for solving the optimization model of flexibility analysis

Pulsipher and Zavala [66] characterized the uncertainty set via multivariate Gaussian random variables for the flexibility analysis of a linear process and formulated a mixed-integer conic programming(MICP)model.If extending ellipsoidal uncertainty sets to the flexibility analysis for microreactors or continuous crystallizers contained end-to-end pharmaceutical manufacturing process,much more complex mixed integer nonlinear programming than MICP comes out.On the other hand,if we combine the flexibility analysis with controllability analysis,the constraints of the formulated mixed integer dynamic optimization model would contain complex ordinary differential equations or even partial differential equations.Solving complex MINLP model and mixed integer dynamic optimization model is not trial-and-error.Efforts are strongly requested to develop novel algorithms and strategies for solving the optimization model.One approach is to simplify the optimization model through replacing the first-principles models with interpretable surrogates.Another approach is to introduce machine learning methods such as reinforcement learning for accelerating the computational time of branch-and-bound/branch-and-cut algorithms.

7.Conclusions

Reduced research and development expenditure,stable drug quality,decreased time to market,increased economic performance,along with the encouragement from regulations,have promoted the paradigm shift of pharmaceutical manufacturing from batch to continuous mode.Truly complex manufacturing environmental issues call for a more important role of PSE than presented one.QbD and QbC emphasize the significance of ensuring product quality through clarifying the interactions between process design and process operation.Learning from the operability analysis of chemical process,flexibility analysis as the core of the operability analysis,can explicitly set a solid foundation for achieving balance between operation and economic performance in front of uncertainties.

This article intended to evaluate the present activities on flexibility analysis of CPM and to illustrate the opportunities and challenges opened up by further roadmaps of CPM.Through the collaborations between academia and industry,flexibility analysis will play an indispensable role in constructing the economically viable,environmentally benign,and socially beneficial pharmaceutical manufacturing processes.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

The authors gratefully acknowledge the financial support from the Ministry of Science and Technology of China (2018AAA0101602).