航段油耗深度学习高质量区间预测算法

陈静杰，赵华治

(1.中国民航大学 电子信息与自动化学院，天津 300300； 2.中国民航大学 中欧航空工程师学院，天津 300300)

0 引 言

国内外区间预测算法研究可以分为两大类，第一类是基于精确点预测模型和误差分析的区间预测算法[1-3]，第二类是基于数据驱动的区间预测算法[4-6]。目前区间预测算法主要应用在风速[1,4]、风功率[2,3,7]、能量负载[8,9]等的区间预测上，航空油耗区间预测上，只有小样本油耗数据区间上下界预测[10]以及在给定区间覆盖率下的最小样本求解[11]的研究，还没有适用于任意航段的航空油耗区间预测算法的相关研究。

Khosravi等[5]将高质量区间预测原则与神经网络损失函数相结合，提出了上下界估计(lower upper bound estimation，LUBE)方法，且该方法已经应用在了洪水预测[12]，但是LUBE方法与梯度下降法不相容，只能采用不同于梯度下降法的模拟退火算法[13]和粒子群优化算法[14]进行训练，而目前梯度下降法已经成为了神经网络的标准训练方法[15]。Tim Pearce等[6]在LUBE方法的基础上，通过改进神经网络损失函数，提出了深度学习高质量区间预测方法，让算法能够通过梯度下降法进行训练，而且此区间预测算法在不明确数据分布的情况下，依旧具有较优的算法性能。

本文将深度学习高质量区间预测算法应用于航段油耗区间预测上，结合飞机航段油耗数据总数据量大，各航段数据量、数据分布区间不一致的特点，采用初级数据源分类预处理、自适应参数、损失函数改进的方法，对原区间预测算法进行了优化，提出了更适用于航段油耗区间预测这一应用场景的神经网络航段油耗区间预测算法。

各个机型航段油耗数据分布相似，本文采用某航空公司某一年A330实际运行数据进行区间预测模型训练和测试。并在短航程、中航程、长航程中各选择两个典型航段，共计6个航段，用于算法性能定量分析比较。

1 深度学习高质量区间预测算法

1.1 损失函数推导

深度学习高质量区间预测算法(简记为QD)中高质量指在给定置信水平1-α下，训练得到的预测区间覆盖率(prediction interval coverage probability，PICP)满足PICP大于等于1-α， 且训练得到的预测区间平均长度(mean prediction interval width，MPIW)尽可能的小。基于高质量原则可以推导出深度学习高质量区间预测算法的损失函数。

设置输入自变量和目标观测值为X和y，n个数据点，xi∈D是对应于yi的第i个D维的输入量。对于1≤i≤n，待预测的预测区间上下界分别记作预测区间应该以一定比率1-α覆盖所有观测值，其中α取值一般为0.01或者0.05

(1)

设置长度为n的向量K， 其中n为观测值个数，向量中的元素ki∈{0,1} 值由下面公式定义

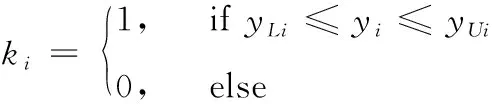
(2)

则，覆盖的观测值总数为

(3)

预测区间覆盖率PICP和预测区间平均长度MPIW由下列公式定义

(4)

(5)

其中，预测区间覆盖率是落在预测区间内的观测值数量与所有观测值数量的比值。预测区间平均长度是所有预测得到的区间长度的平均值，其单位与观测值的单位一致。覆盖率与设定的置信水平差异越小，算法性能越优；覆盖率相近，预测区间平均长度越短，算法性能越优。

对于PICP，采用最大似然法，根据K和α寻找使得神经网络的最优参数θ

(6)

其中，K中的每个元素ki可以看作伯努利随机变量，即ki～Bernoulli(1,1-α)。 同时可以进一步假设每个元素ki满足独立同分布，那么预测区间覆盖总数c可以看作满足二项式分布，即c～Binomial(n,(1-α))， 此时似然函数可以写为

(7)

根据中心极限理论(特别是Moivre-Laplace theorem)，对于较大的数据量n，二项式分布可以近似看作正态分布

(8)

采用负对数似然函数Negative Log Likelihood(NLL)最小化代替似然函数最大化，因此式(8)可以简化为

(9)

只考虑当PICP<(1-α) 时的单边损失，综合考虑预测区间长度和覆盖率的重要性。因此结合式(5)和增加惩罚系数λ的式(9)得到数据驱动的损失函数

(10)

由于式(4)PICP中的ki为阶梯函数，则损失函数LossQD在部分点处不可导，不满足梯度下降法的条件，因此利用Sigmoid函数σ对ki进行柔和化处理，使其处处可导。其中s为放大系数

(11)

1.2 构建神经网络

(12)

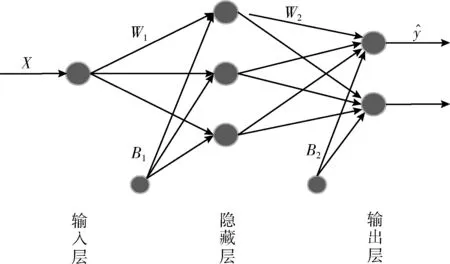
图1 神经网络区间预测模型结构

(13)

2 改进的航段油耗区间QD算法

深度学习高质量区间预测算法损失函数中的区间覆盖率项由概率论相关定理推导而来，进行柔和化处理之后，加上平均区间长度项得到损失函数。从损失函数式(10)可以推导出，高质量区间预测算法在航段油耗预测这一应用场景下存在以下不足：

(1)该损失函数在训练过程中只需要满足预测区间覆盖率大于1-α， 就能得到预测区间覆盖率项最小值，因此训练得到的区间覆盖率不一定接近设定的置信水平。而在航段油耗区间预测时需要满足预测的区间覆盖率非常接近设定的置信水平值，同时保证平均区间长度尽可能的小。

(2)初始区间覆盖率项、平均区间长度项在该损失函数中的权重随着训练样本数变化而变化，算法普适性较差，区间覆盖率项、平均区间长度项在训练时无法平衡，会出现偏向某一项的情况，最终导致预测模型的结果不满足最初的需求。

因此在深度学习高质区间预测算法基础上，结合航段油耗数据量以及数据分布特点对原区间预测算法进行了如下改进。提出了更加适合航段油耗预测这一应用场景的航段油耗深度学习高质量区间预测算法。

2.1 训练数据优化

航段油耗数据分布情况如图2所示，可以看出航段油耗数据具有各航段数据量不一致、分布区间不一致、总数据量大的特点。

图2 航段油耗分布

根据损失函数式(10)和第3章中QD算法定性定量结果可以推导出，如果考虑全局预测区间覆盖率和平均预测区间长度，采用全部样本直接训练，会出现整体达到最优解而各航段不满足预期的情况，同时相同置信水平和平均区间长度下存在多种最优解，导致多次训练得到的结果不一致且差异较大。因此QD算法在航段油耗区间预测时稳定性和可靠性较低，不同航段下算法性能差异较大，需要进行优化改进。

首先对训练数据进行优化，将初级数据源按不同航段或者航段大圆距离进行分类，统计各航段数据量。同时针对各航段油耗分布范围不一致的特点，将所有训练数据进行无量纲化处理，提高算法的普适性。用各个航段的数据进行训练以得到合理油耗的上下界。

2.2 算法改进

(14)

(15)

其中，MAX,MIN是观测值y无量纲化时设定的最大最小值，K，L是常数，K是用来增加覆盖率项的权重，可以降低预测覆盖率和置信水平之间的最大差值，L的取值范围2到5用来略微扩大相邻观测值间的差异。

通过观察原损失函数公式，可以进一步将max(0,(1-α)-PICP)2优化成max(0,(1-α)-PICP)， 这样既能解除前文提到的多样本数限制，又能减缓损失函数值波动，使其尽快达到最优值且趋于平稳。将新的惩罚系数λ代入式(10)中，得到新的损失函数计算公式。最后使用新的损失函数构建新的神经网络航段油耗区间预测模型

(16)

在定义新的惩罚系数λ和放大系数s之后，能让不同样本数下的初始区间长度项和区间覆盖率项在相同量级，且PICP接近理论值，增加了算法的普适性。设定的K，L值能让模型在训练过程中，优先保证区间覆盖率非常接近设定的置信水平值，然后使得区间长度最短，达到最优解，提升了算法的可靠性。上述设定使得多次训练的损失函数最小值非常接近，预测的结果也非常接近，算法稳定性增加。

3 实验结果分析与比较

前已述及原深度学习高质量区间预测算法记作算法QD，下文将训练数据优化后的算法记作算法QD_data，将最后改进得到的航段油耗深度学习高质量区间预测算法记作算法QD_fuel。随机选取实验数据的80%作为训练数据，采用3种区间预测算法进行建模，设置置信水平为90%，每种算法进行3次训练，对所有训练结果进行定性和定量的分析和比较。

3.1 实验结果定性分析与比较

将训练得到的油耗区间上下界以及训练过程中的损失变化值进行可视化，得到如图3和图4所示实验结果。

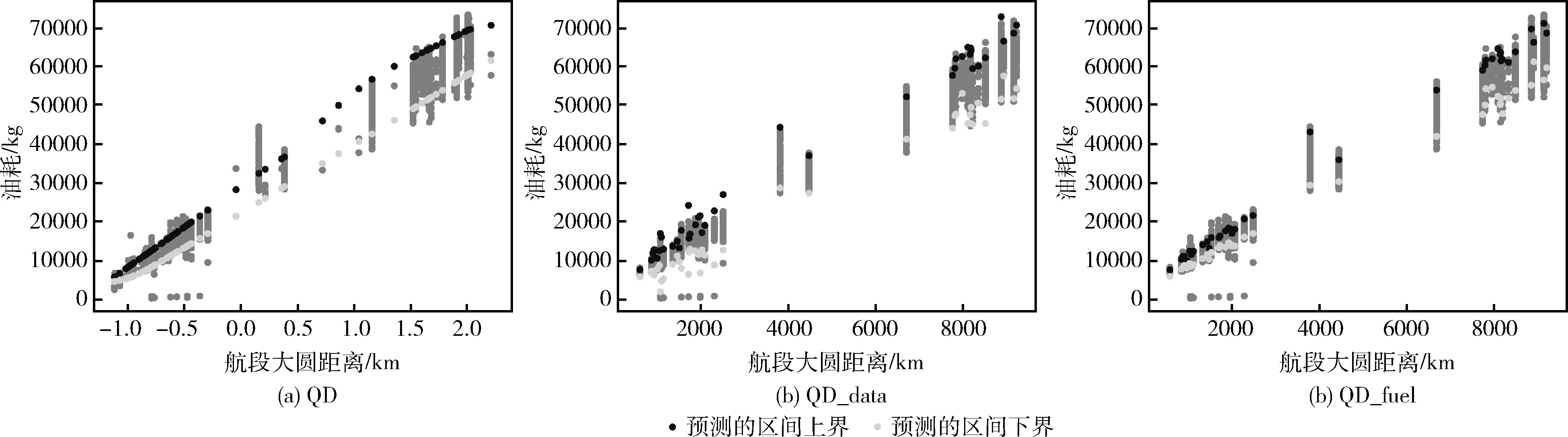
图4 航段油耗区间预测结果

QD算法仅考虑全局覆盖率和平均区间长度，经一次训练得到各航段预测结果，训练过程中损失函数值变化情况如图3(a)所示，QD_data和QD_fuel算法，分别训练各航段油耗数据得到预测结果，各航段训练过程中的损失函数值变化情况如图3(b)、图3(c)所示。

从图3(a)可以看出，损失函数值趋于最小值且已经平稳，说明这是该区间预测模型训练得到的最优结果，但是从图4(a)可以看出，原区间预测算法训练得到各个航段的区间覆盖率差异较大，有的航段PICP≈100%， 有的航段PICP≪(1-α)。 如果用于航司所报告油耗数据合理性判断，会出现部分航段大量出现不合理数据，部分航段几乎没有不合理数据的情况，对于不同航段算法普适性、可靠性均较低；从图3(b)可以看出，损失函数值在训练过程中一直在波动，部分航段在训练结束时损失并未趋于稳定和最小值，说明该区间预测模型未能训练出最优结果，从图4(b)可以看出，通过训练数据优化，算法普适性和可靠性有所提高，但是仍有部分航段出现未能训练出结果或者训练结果陷入局部最优的情况；从图3(c)中损失函数值的变化可以看出，所有航段均能趋于稳定且到达最优解，从图4(c)可以看出，所有航段均未发现异常训练结果，算法普适性和可靠性进一步提高。

3.2 实验结果定量分析与比较

本文选用预测区间覆盖率PICP和无量纲化平均预测区间长度(nondimensionalized mean prediction interval width，NMPIW)两个区间预测算法性能定量评价指标对算法进行定量分析和比较

(17)

其中，R为人为设定的观测值区间长度参考范围。无量纲化平均预测区间长度是平均预测区间长度与参考的观测值区间长度R的比值。

6个航段3次训练得到的实验结果见表1～表3。QD、QD_data、QD_fuel训练得到的全局预测区间覆盖率分别为0.9104，0.9185，0.9004；全局预测区间平均长度6750.59(kg)，7022.88(kg)，6503.51(kg)。

从表1和表2中单次训练的结果可以发现QD算法和QD_data算法训练得到的预测覆盖率PICP不在设定的置信水平周围，算法可靠性较低。从表1和表2中多次训练得到的实验结果可以发现由于神经网络模型结构特性以及随机生成的权重、偏置等参数的影响，神经网络区间预测模型存在模型不确定性，实验结果容易陷入局部最优，或者在设定的有限迭代次数下达不到最优解，导致不同次训练得到的结果差异性较大，算法本身稳定性低。

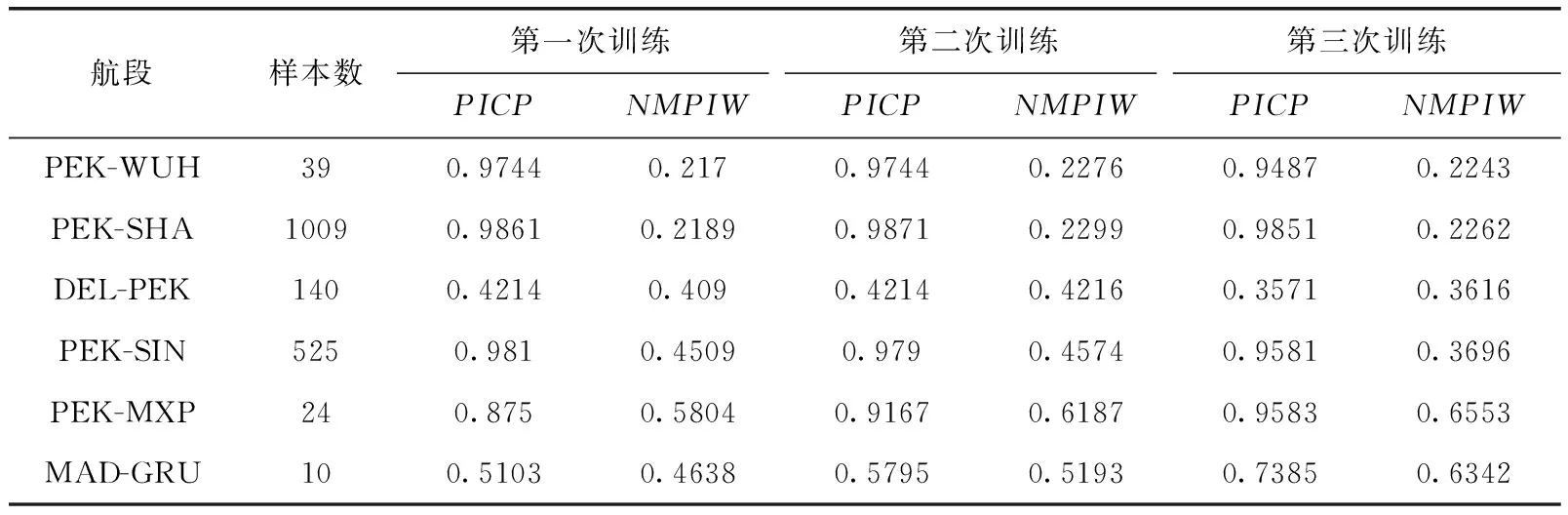
表1 QD算法PICP和NMPIW结果对比

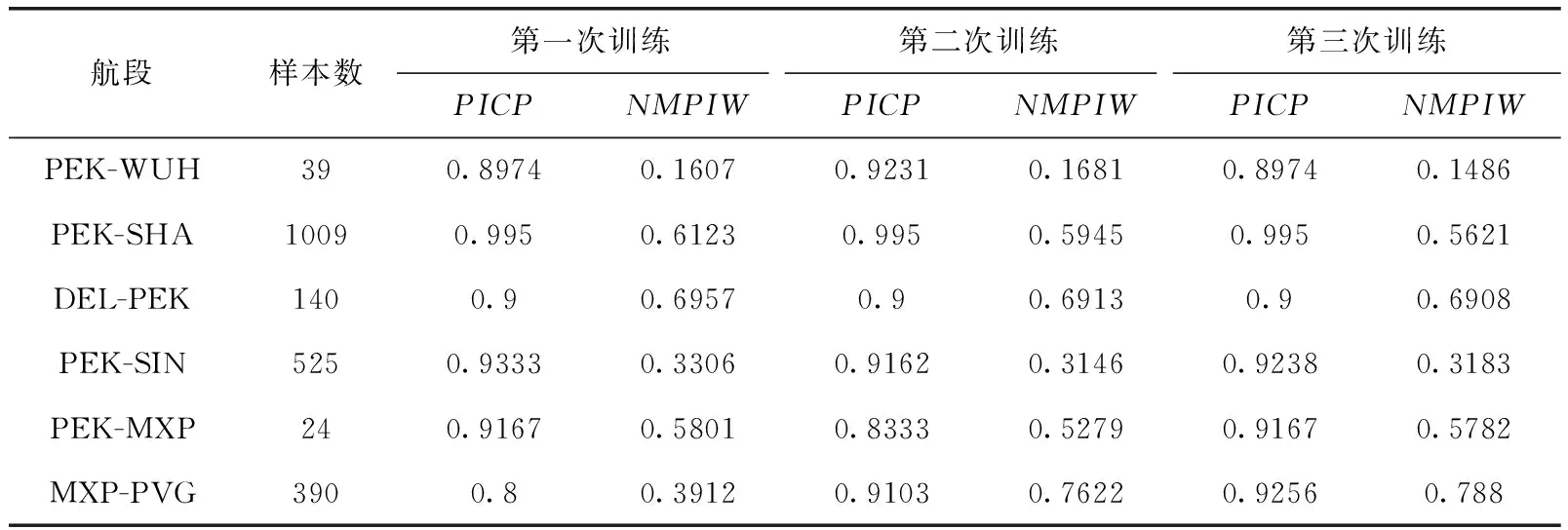
表2 QD_data算法PICP和NMPIW结果对比

表3 QD_fuel算法PICP和NMPIW结果对比

从表3可以看出，改进后的区间预测算法训练得到的预测区间覆盖率PICP均在设定的置信水平周围，无量纲化区间长度NMPIW明显减小，不同次训练得到的PICP变化上下不超过1个数据点引起的覆盖率变化，同时不同次训练得到的无量纲化区间长度NMPIW变化不超过1%，因此算法可靠性、稳定性明显提升。此外改进后的算法普适性增强，对不同训练样本数、不同数据分布的各个航段均具有较优的可靠性和稳定性。

为了进一步验证本文算法的有效性，引入基于伽马函数近似的参数估计区间预测算法以及LUBE算法，其中基于伽马函数近似的区间预测算法记作Gamma算法，是一种先对航段历史数据通过伽马函数近似拟合得到数据分布参数，然后根据置信水平进行区间预测的算法。LUBE算法是以区间覆盖率和宽度的综合指标(coverage width-based criterion，CWC)作为损失函数，构建单输入、单隐藏层、双输出的区间预测神经网络模型，然后通过粒子群算法中粒子个体与群体之前的信息相互，不断更新位置和速度信息，最终得到最优训练结果，实现区间预测模型构建。

Gamma算法的优点在于拟合了各航段数据分布情况、计算效率高、没有模型不确定性。算法缺点为仅考虑了区间覆盖率，根据设定的置信水平分配两边覆盖率时，分配方法没有明确的依据，现在常用的双边均分不一定合理，而且Gamma算法只能用于单影响因素区间预测。LUBE算法的优点为损失函数综合考虑了预测区间覆盖率和预测区间长度，损失函数不需要处处可导，粒子群算法在足够粒子数和迭代次数下可以得到全局的最优解。算法缺点在于粒子群中粒子的初始位置和速度随机生成，达到最优解所需的粒子数和迭代次数不确定度高，导致在有限粒子数和迭代次数下训练得到的最优解不一致，算法不确定度高，同时算法运行时间长，计算效率低。LUBE算法3次训练得到的实验结果见表4。

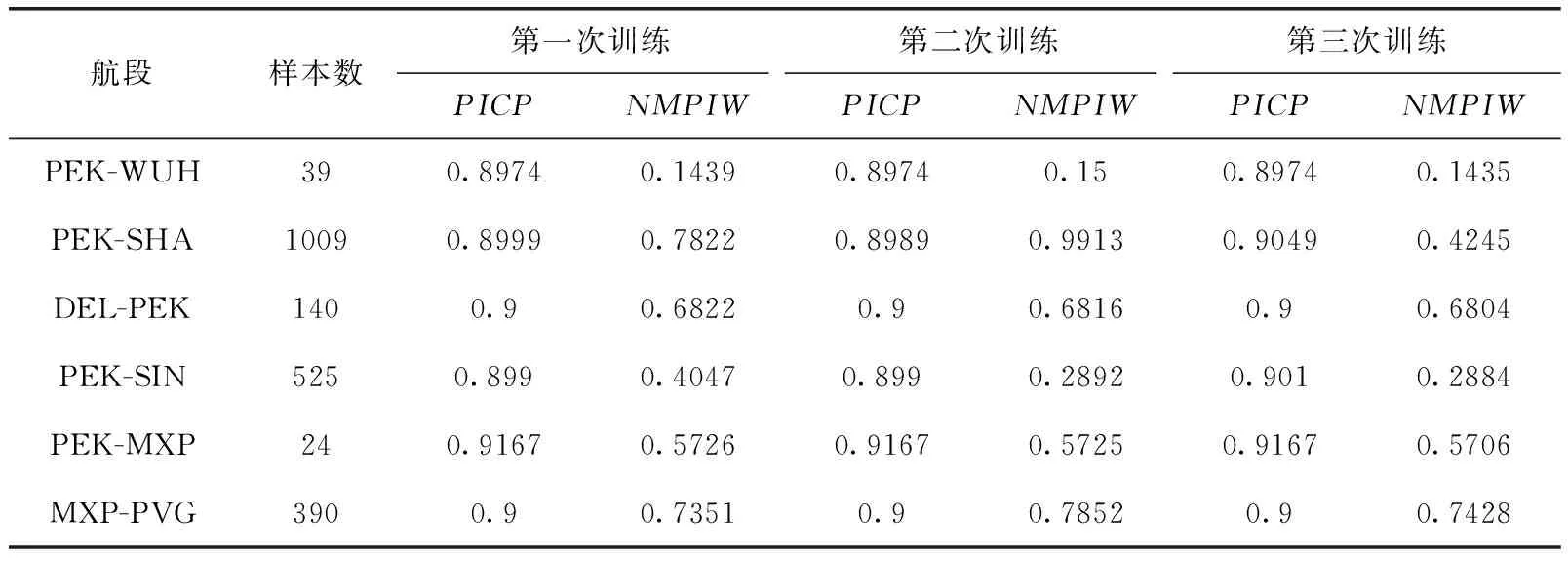
表4 LUBE算法PICP和NMPIW结果对比

选择PICP值、MPIW值以及算法运行时间t作为算法性能的定量评价指标，设计部分航段和所有航段的算法性能测试实验，在置信水平为90%时相同训练样本及测试样本情况下的算法性能对比结果见表5、表6。

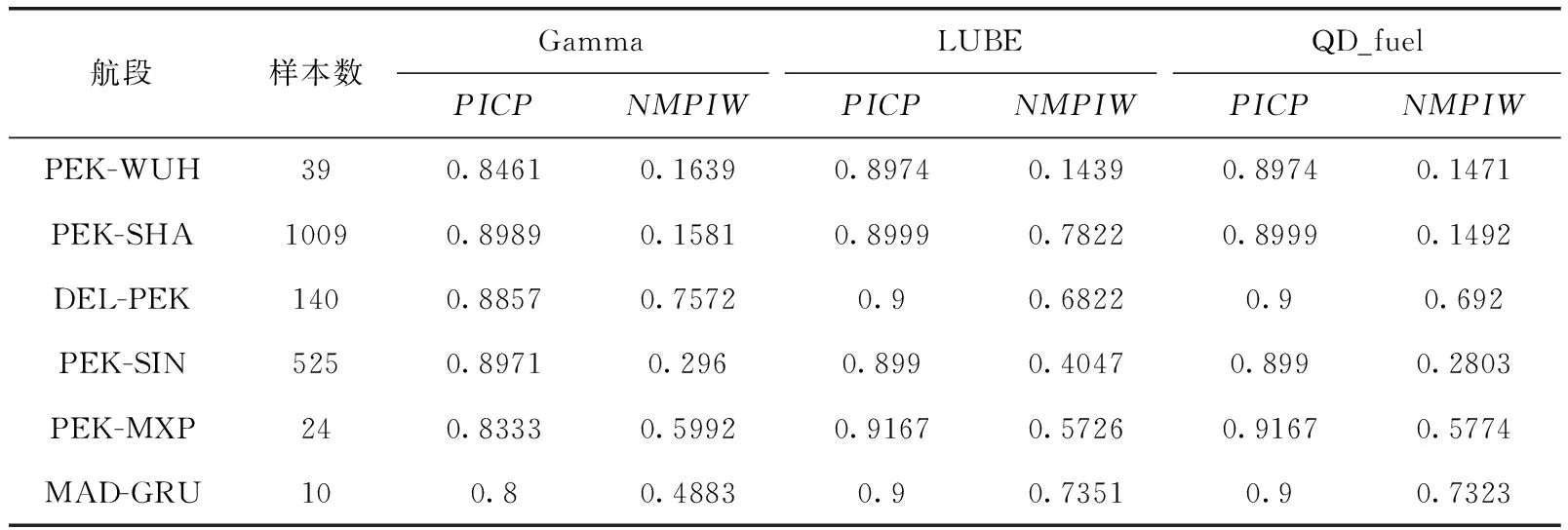
表5 PICP和NMPIW部分航段预测结果对比

表6 PICP、MPIW和t全局预测结果对比

从表4中LUBE算法不同次训练得到的结果可以看出，在较少粒子数和迭代次数下，样本数较多的航段未能训练得到最优解，同时粒子初始化参数随机获取，在未能达到全局最优时，不同次训练得到的区间长度差异较大，算法的稳定性较差。从表6中可以看出LUBE算法的运行时间较长，如果增加粒子数和迭代次数，会进一步降低算法运行效率，在样本数较少的航段出现计算资源浪费的情况。此外粒子数和迭代次数的选择没有可靠的依据，只能通过反复实验得到平衡计算效率和计算精度的最优参数。

从表5中Gamma算法预测结果可以看出，在样本数较少的航段，由于样本数较少，航段数据分布特点不明显，导致Gamma函数近似拟合的效果较差，预测结果不理想，因此Gamma算法在数据量较少的航段的可靠性较差。

从表5、表6中部分航段和全局预测结果可以看出Gamma算法的计算效率最高，但是只考虑了预测区间覆盖率，因此计算得到的平均区间长度较长，算法可靠度较低，对于数据量较少的航段，可靠性更低，算法不适用于小样本区间预测。LUBE算法得到的区间覆盖率接近设定的置信水平而且平均区间长度较小，但是算法运行时间较长，计算效率不高，同时最优粒子数和迭代次数难以确定，需要平衡算法稳定性和算法运行效率。本文算法得到的区间覆盖率最接近设置值，且平均区间长度最短，计算效率较高，对于任意数据量的航段，均能实验最准确的预测。因此本文算法的可靠性最高，算法综合性能最好。

4 结束语

本文将初级数据源按航段进行分类并进行无量纲化处理，构建可以根据样本数、设定的置信水平、设定的无量纲化范围自适应惩罚系数和放大系数的损失函数，提出了航段油耗深度学习高质量区间预测算法。实验结果表明，设定的置信水平为90%时，各航段的预测覆盖率均在置信水平附近，总区间覆盖率为PICP=0.9004， 预测区间平均长度6503.512(kg)，较改进前算法、Gamma算法、LUBE算法减少200(kg)到500(kg)，预测区间覆盖率最接近设定的置信水平值。本文所提出的航段油耗深度学习高质量区间预测算法具有较优的可靠性、稳定性和普适性。预测的航段合理油耗区间，可以用来对航司所报告油耗数据进行合理性判断，并作为碳核查辅助工具基础。此外航段油耗深度学习高质量区间预测算法可以进一步扩大应用场景，用于多影响因素，更精确的航段油耗区间预测，未来将引入航向、业载、飞行时间等多个影响因素，研究各航段多影响因素下区间预测算法的预测效果，得到更为合理可靠的油耗区间。