应用于大数据的Trie树排序算法

赵林洁，肖 英+，张 宇

(1.中国计量大学 信息工程学院，浙江 杭州 310018；2.中国计量大学 浙江省电磁波信息技术与计量 检测重点实验室，浙江 杭州 310018；3.杭州代码哥智能科技有限公司 研发中心，浙江 杭州 310018)

0 引 言

据统计，2018年全球数据量总和33 ZB(1 ZB=1万GB)，国际数据公司发布的最新版白皮书《Data Age 2025》预测2025年全球数据量总和将达到175 ZB[1]，该数据总量正在以指数级速率增长，这意味着数据分析和处理对算法提出了更高的要求，排序是数据处理的核心运算，涉及到人工智能[2]、机器学习[3]、模式识别[4]和大数据[5]等领域，然而面对数据量剧增的现象现有的排序算法已经无法满足当下数据处理的需求，迫切需要一个在动态增加数据的场景下时间、空间性能更优的排序算法。

排序是将一个任意序列重新排成一个按某种规则排列的有序序列[6]。如冒泡排序、选择排序、插入排序等传统排序算法以两两之间的比较为基础，时间复杂度为O(n2)，这些基于“比较”的排序算法在最坏情况下能达到的最优时间复杂度为O(nlogn)[7]。快速排序算法是采用分治策略，通过递归的方式将待排数据根据基准值分割成大小两部分，直到数据变成有序序列[8]，其时间复杂度为O(nlogn)。该算法结构简单，平均性能较佳，是多数排序应用的最佳选择[9]，但是如果在排序过程中动态添加和删除数据时，该算法性能大大降低。而堆排序算法是利用堆积树结构设计的一个完全二叉树，时间复杂度为O(nlogn)[10]。该算法通过树形结构保存部分比较结果，从而减少了比较次数，但是在实际应用中频繁更新数据时，每次更新都需要重做一遍堆的维护，这非常费时[11]。文献[12]中的AVL树(Adelson-Velsky-Landis Tree)解决了数据频繁更新的问题，该结构所有节点左右子树的高度差不超过1，插入时间复杂度为O(nlogn)。虽然AVL树支持数据动态更新，但其追求绝对平衡，每次插入新节点后旋转次数无法预知，且为维护AVL树高度平衡付出的代价太大[13]，故而不实用。文献[14]中提出的红黑树是AVL树的变形，该算法只追求大致平衡，保证每次插入节点最多3次旋转达到平衡，与AVL树时间复杂度相差不大，应用更为广泛，是多种编程语言底层实现采纳较多的数据结构，如实现C++、Java、C#等类库中的Map、Set结构的底层[15]。然而红黑树的高度随着数据量的增加而增加，红黑树的查找性能会逐渐降低，且每次进行插入、删除时都需要自底向上调整使新的二叉树满足红黑树的性质，耗时较多。因而，需要一种在海量数据下查找性能稳定且空间效率更高的算法结构。

因此，本文提出了一种16-bit Trie树排序算法，该算法借助16-bit Trie树结构利用邻居节点找到临近的链节点指针进行插入排序。在构造Trie树时，该算法使用动态数组存储子节点指针，避免了固定数组存储子节点时的空间浪费，并且引入了词缀压缩方法使该算法在处理大规模数据时更具突出优势。

1 16-bit Trie 树排序算法

16-bit Trie树结构在构造Trie树时使用16 bit表示子节点信息，每个节点至多有16个子节点，因此，命名为16-bit Trie树。16-bit Trie树排序算法是在16-bit Trie树结构上利用邻居节点保存的链节点指针L，将新增加的链节点指针插入到链节点L处完成排序。接下来，本节将具体介绍16-bit Trie树排序算法进行数据排序的过程。

1.1 基本定义

16-bit Trie树结构的节点信息定义见表1。

根据表1描述16-bit Trie树结构从父节点索引到子节点。首先，构建一个二维数组LeafsInfoMap映射表见表2，

表1 节点信息定义

行表示子节点状态，列表示当前节点状态下第i个子节点(i=0表示子节点不存在)。关于LeafsInfoMap映射表有两种操作：LeafsInfoMap[leafsInfo][nodeValue]表示在leafsInfo状态下值为nodeValue的子节点位置，LeafsInfoMap[leafsInfo][17]表示leafsInfo的子节点总数。其次，根据表1中的两个数组leafsInfo和leafs，构建父节点、子节点，leafsInfo和leafs是对应关系。例如，父节点的leafsInfo为5(二进制为0000 0000 0000 0101)，表示父节点有两个子节点，值为0的子节点和值为2的子节点，分别存储在leafs[0]和leafs[1]。由于子节点存储在leafs数组中，通过leafs[LeafsInfoMap[leafsInfo][nodeValue]-1]可以从父节点索引到值为nodeValue的子节点。如上述例子，父节点的leafsInfo为5，如表2所示，通过LeafsInfoMap[5][0]=1可以找到值为0的子节点是父节点的第1个子节点，保存在leafs[0]中；通过LeafsInfoMap[5][2]=2可以找到值为2的子节点是父节点的第2个子节点，保存在leafs[1]中。以上可以看出，利用leafsInfoMap映射表和节点的leafsInfo信息可查询当前节点下的所有子节点信息。

此外，16-bit Trie树结构在构造Trie树时使用动态数组leafs存储子节点指针，其数组大小随着子节点数的变化而变化。如上例中，父节点再添加值为1的子节点时，leafsInfo变为0000 0000 0000 0111，而leafs数组长度变为3，分别存储3个子节点指针。

1.2 算法描述

16-bit Trie树排序算法是利用16-bit Trie树中的邻居节点查找邻近的链节点指针L，将新链节点指针插入到链节点L处，从而完成链表排序。传统的Trie树是先构建后遍历完成数据排序，而16-bit Trie树排序是边构建边排序，完成构建树的同时完成链表排序。为了进一步提高16-bit Trie树排序算法的时间性能，引入词缀压缩方法，在能区分不同关键字的情况下，最大限度地减少构建的节点数，从而提升排序速度，16-bit Trie树排序算法的流程如图1所示，具体实施步骤如下：

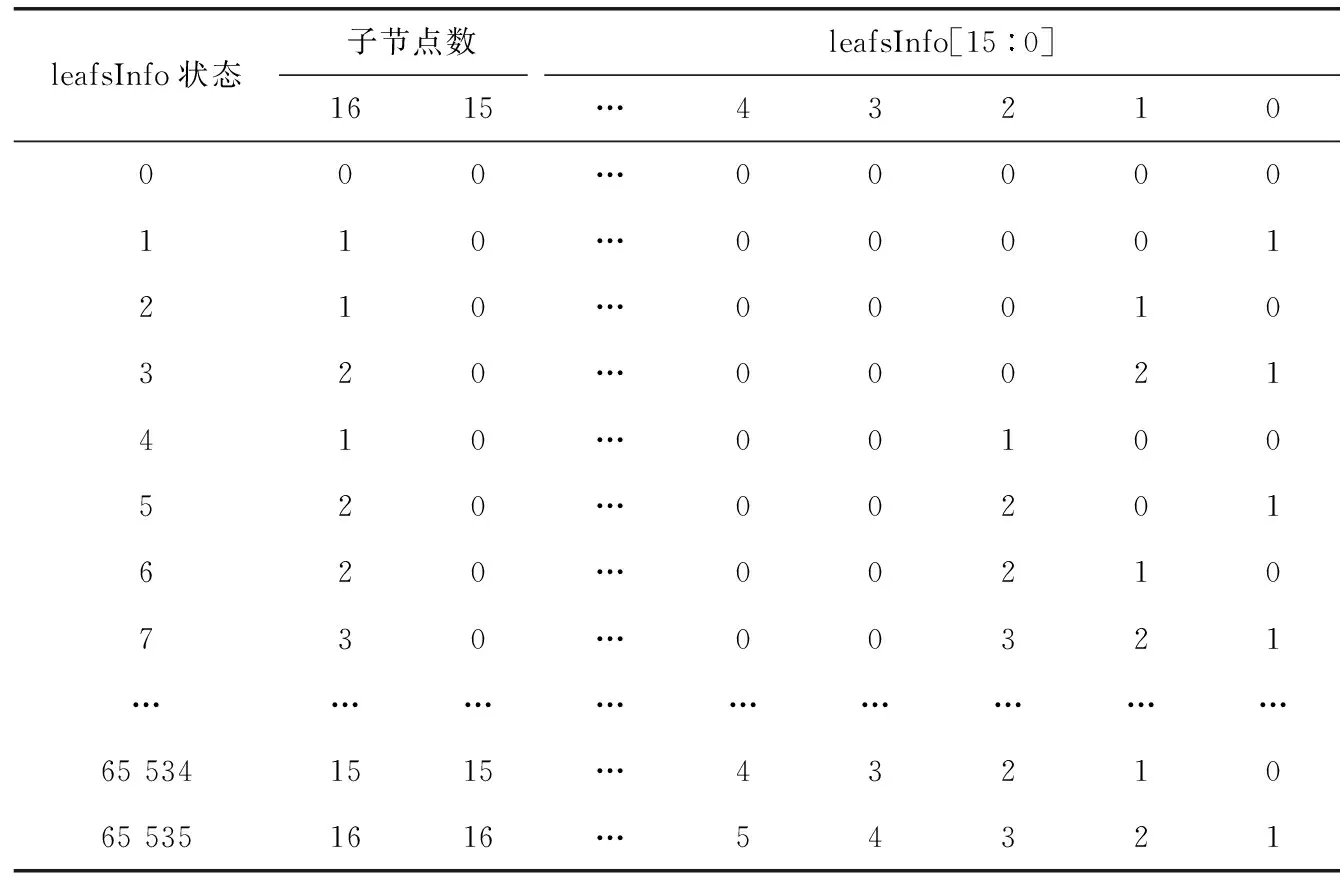
表2 LeafsInfoMap映射

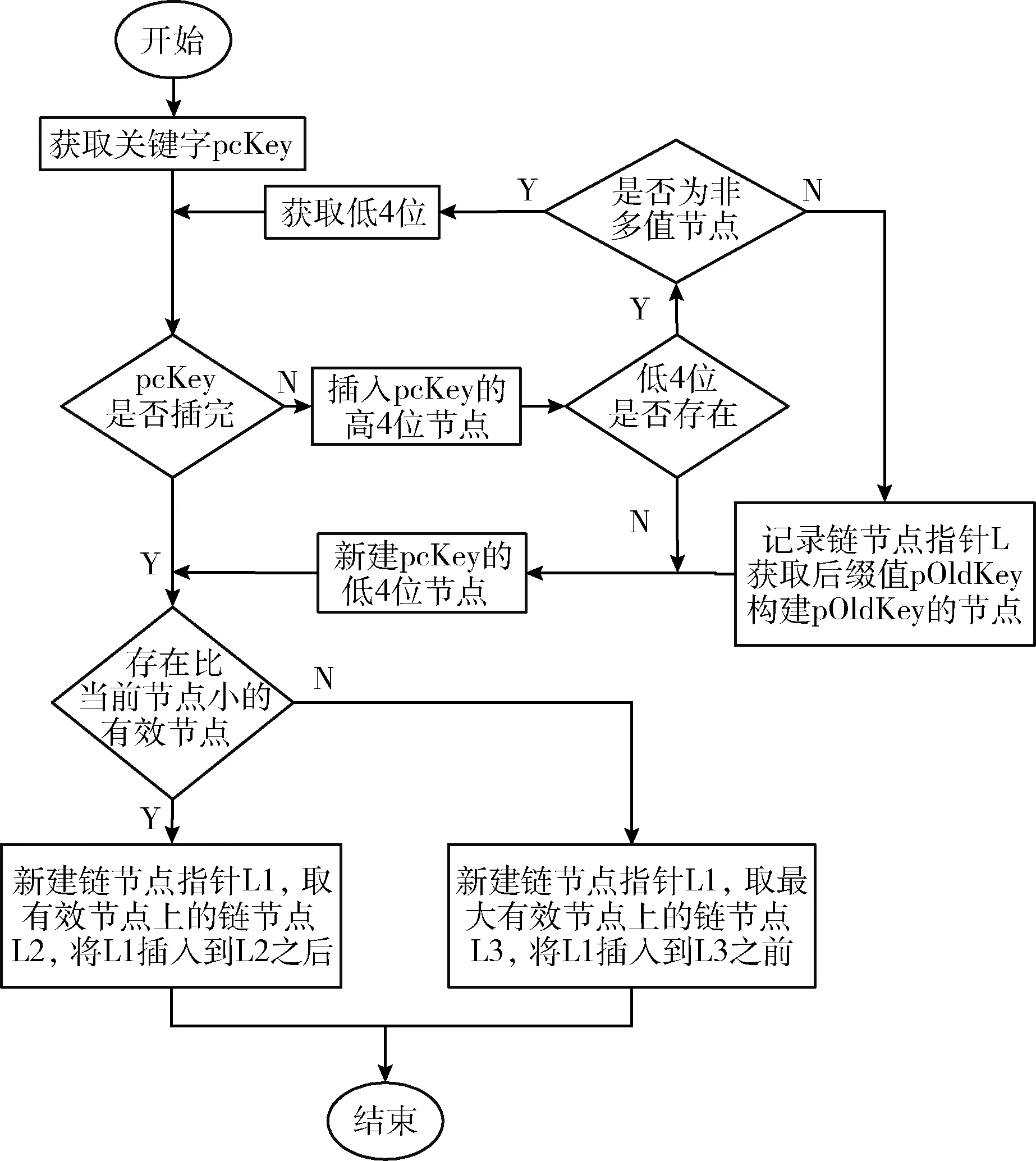
图1 算法流程

例如，关键字集合K={‘de’，‘fg’，‘dec’，‘dea’，‘ta’} 进行16-bit Trie树排序的过程。首先初始化16-bit Trie树结构和排序链表如图2(a)和图2(b)所示，正方形表示根节点，圆形表示链节点。在图2(a)中根节点Root没有子节点，leafsInfo占16 bit的空间其值为0，由于没有子节点leafs数组不占用空间，其leafsInfo、leafs数组，如图3(a)所示。

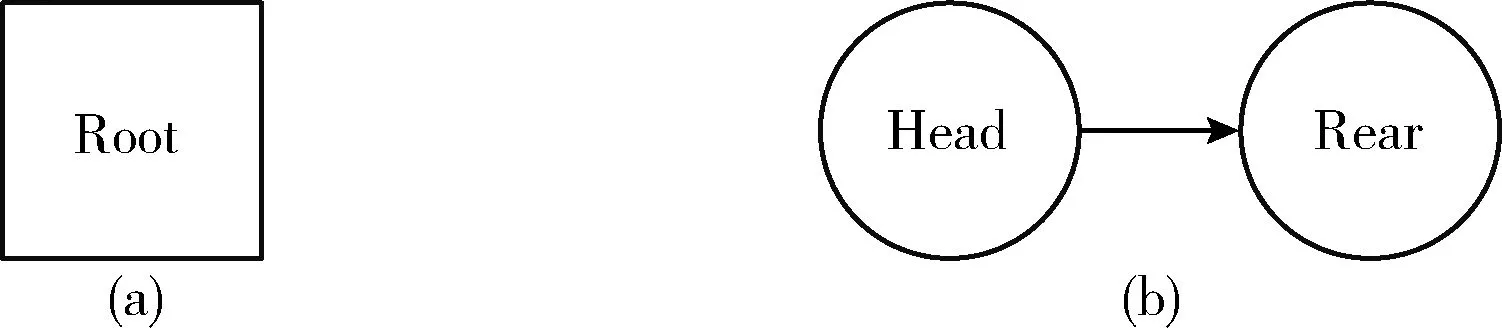
图2 16-bit Trie树结构和空链表

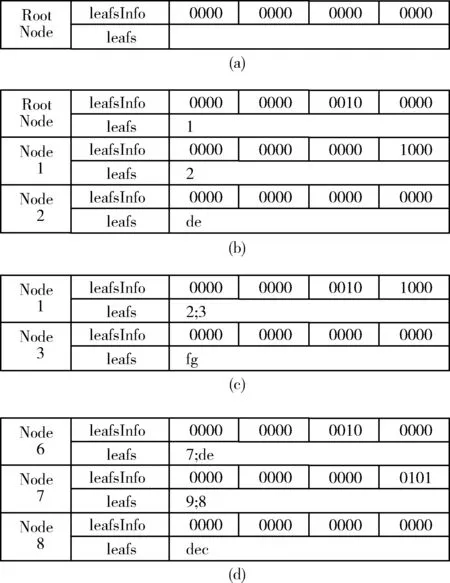
图3 节点信息的变化情况

插入第一个关键字‘de’，如图4(a)所示构建16-bit Trie树结构，图中六边形表示子节点，十六角型表示多值节点，在16-bit Trie树结构上实现排序的具体步骤如下：

(1)获取关键字‘de’，当前节点定位至根节点Root；

(2)判断关键字‘de’并未完全插入；

(3)取d的高4位记作d high_4bits，将根节点leafsInfo的第d high_4bits位置1，在根节点leafs数组的第LeafsInfoMap[leafsInfo][d high_4bits]-1个位置保存节点1，根节点的leafsInfo、leafs数组由图3(a)变到图3(b)；

(4)当前节点定位至节点1，取d的低4位记作d low_4bits，判断关键字长度大于1，创建一个多值节点2，将leafsInfo的第d low_4bits位置1，leafs中的第LeafsInfoMap[leafsInfo][d low_4bits]-1个位置保存节点2，在节点2的AdressNode数组中存储词缀‘e’，节点1的leafsInfo、leafs数组如图3(b)所示，转至(5)；

(5)当前节点定位至节点2，由于父节点不存在，新建链节点‘de’，在节点2的leafs[0]中存入链节点指针‘de’，将链节点‘de’插入到头节点‘Head’之后尾节点‘Rear’之前，节点2的leafsInfo、leafs数组如图3(b)所示，链表排序结果如图4(b)所示。

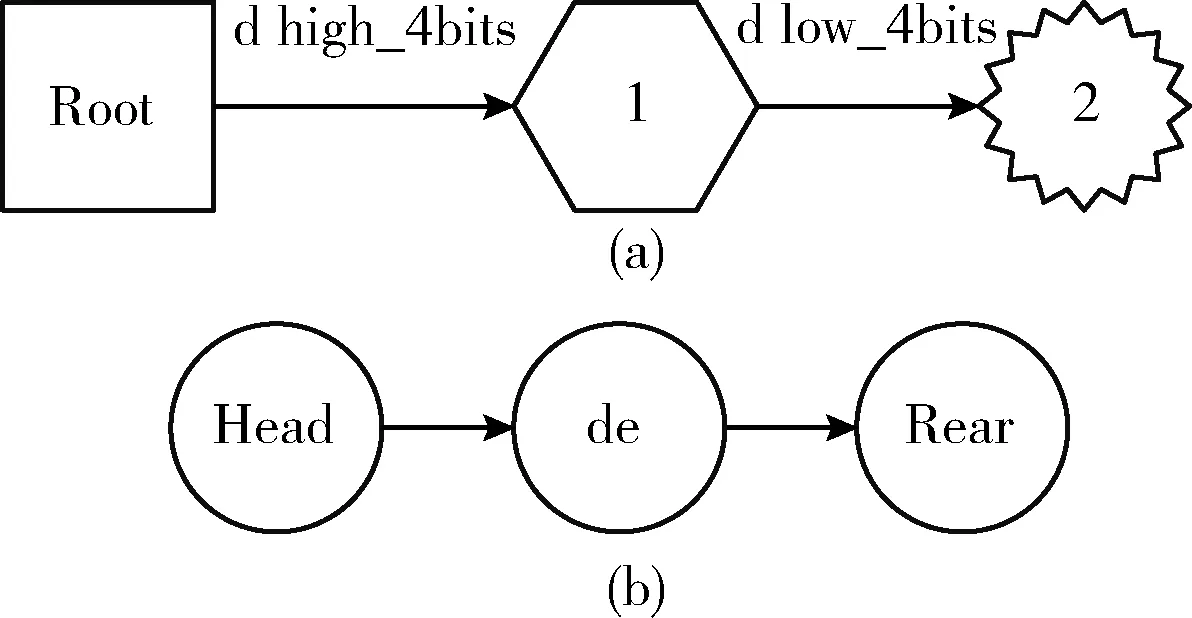
图4 添加关键字‘de’

为了观察当前节点如何借助邻居节点完成链表排序，插入第二个关键字‘fg’，如图5(a)所示。根节点Root的leafsInfo、leafs数组保持不变，节点1的子节点是节点2和节点3，leafs数组长度为2，节点1的leafsInfo、leafs数组由图3(b)变到图3(c)。节点3是多值节点，其数组AdressNode保存词缀‘g’，新建链节点指针‘fg’，通过父节点(节点1)查找到邻居节点(节点2)，取节点2上的链节点指针‘de’，将新建的链节点指针‘fg’插到链节点指针‘de’之后，如图5(b)所示完成链表排序，最后将链节点指针‘fg’保存在节点3的leafs[0]中。

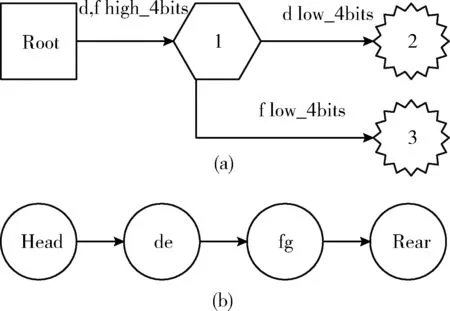
图5 添加关键字‘fg’

按上述方法插入集合K中所有数据，16-bit Trie树结构和链表排序结果如图6(a)和图6(b)所示，图中用菱形表示有效节点，各节点的leafsInfo、leafs数组如图3(d)所示。由于关键字‘de’和‘dea’共用一条路径，为了区分关键字‘de’和‘dea’，设置了有效节点标记位，如图6(a)所示，节点6、节点9分别是‘de’和‘dea’的有效节点，从根节点到有效节点代表一条完整的路径，即可根据有效节点区分同一路径上不同的关键字‘de’和‘dea’。多值节点是特殊的有效节点，是保存了词缀的有效节点，在必要情况下需要取多值节点的词缀再构建新节点。

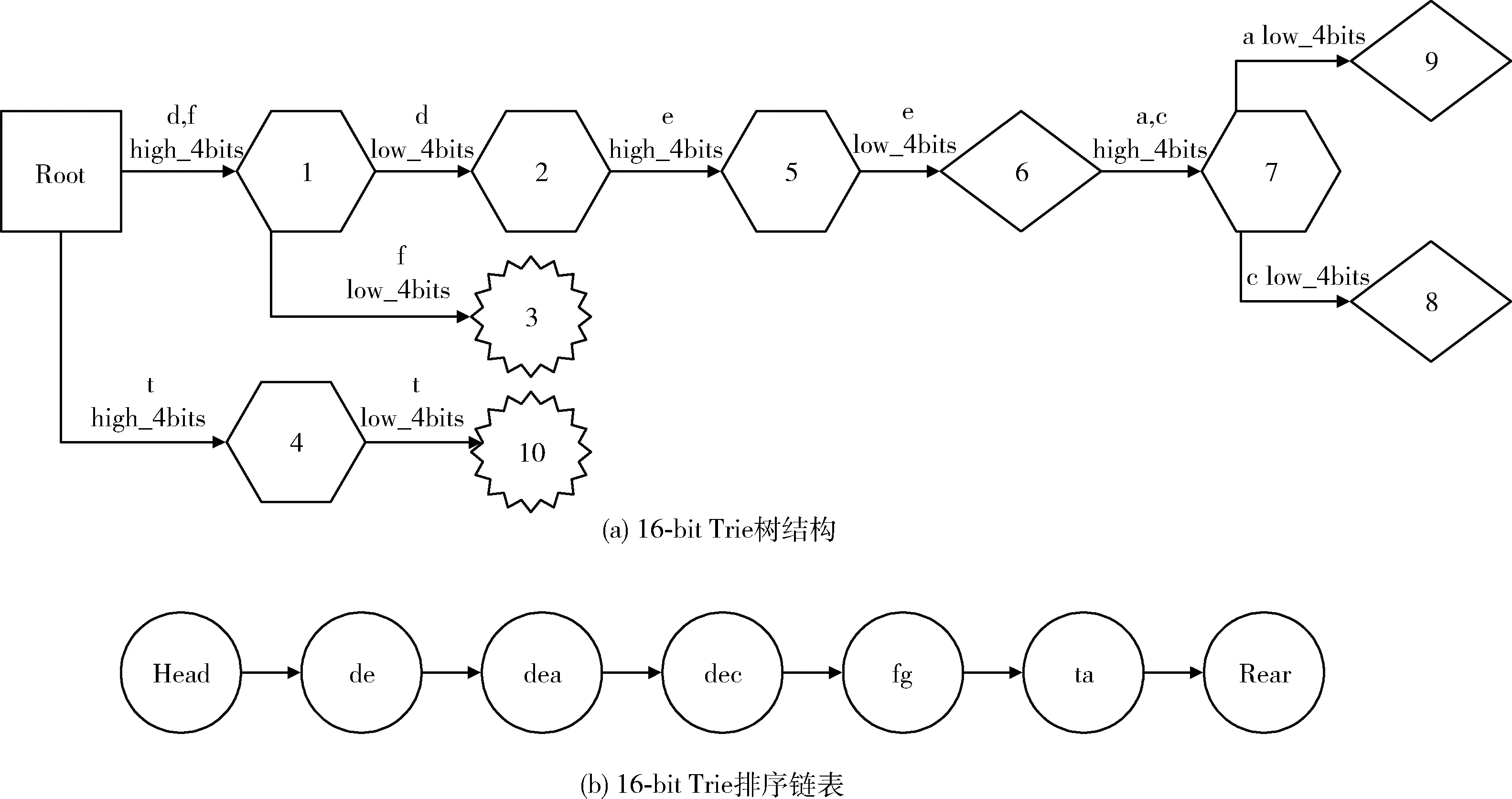
图6 16-bit Trie结构和16-bit Trie排序链表

2 结果分析

本文的测试环境为Windows操作系统Intel(R) Core(TM) i7-8700CPU @3.20 GHz 3.19 16 GB内存的PC机上测试，编译器为Visual Studio 2019，使用C++语言编程，用GetTickCount()函数来统计实验中各操作所消耗的时间，为了减小测试误差，测试的时间均取5次测试的平均值。

本文采用与快速排序算法、传统Trie树对比的方式来评估16-bit Trie树排序算法的时间性能。快速排序算法采用C标准库函数qsort实现动态数据排序，传统Trie树采用26叉树实现字符串排序。本文的测试数据是使用MATLAB生成的由英文字母a-z组成的任意长度的随机字符串，测试数据分为定长、定量2种数据，定长数据是字符长度均为15字符的随机数据；定量数据是指数据量固定、字符长度变化的数据。通过以上2种测试数据对快速排序、16-bit Trie树排序、传统Trie树的排序时间进行测试并分析其时间性能。

2.1 定长数据

表3对3种算法在数据长度为15字符时的排序时间进行了记录。从表3可以计算出，当数据量从150万增加到550万时，3种算法的排序时间分别增加了68.6倍、14.4倍、3.9倍。传统Trie树排序增长倍数最小，但初始排序时间开销较大，整体排序时间用时较多；16-bit Trie树排序次之，而快速排序在数据动态增加时排序时间增长最快。

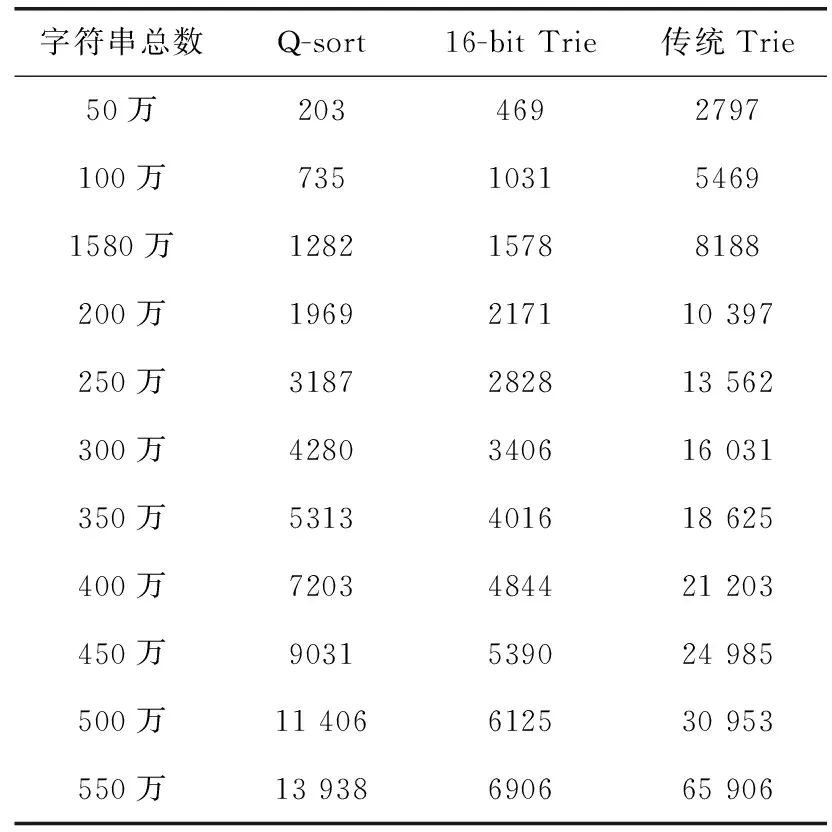
表3 定长数据的排序时间/ms

图7是数据长度为15字符时快速排序、16-bit Trie树排序和传统Trie树排序从初始50万数据量逐次增加50万至550万时花费的排序时间。如图7所示，传统Trie树、16-bit Trie树都需要构建Trie树且排序时间都呈线性增长，16-bit Trie树的增幅比传统Trie树的增幅小，且整体排序时间开销也较少。与快速排序相比，16-bit Trie树排序算法在数据量较小时耗时多，是因为构建16-bit Trie树结构花费较多时间，而快速排序算法无需构建直接进行排序，故而快速排序算法在数据量较小时耗时少。从图7可以发现，当数据量动态增加到250万时，16-bit Trie树排序算法的时间开销与快速排序接近；当数据量动态增加到400万时，比快速排序快27%；当数据量进一步增加到550万时，比快速排序快45%。

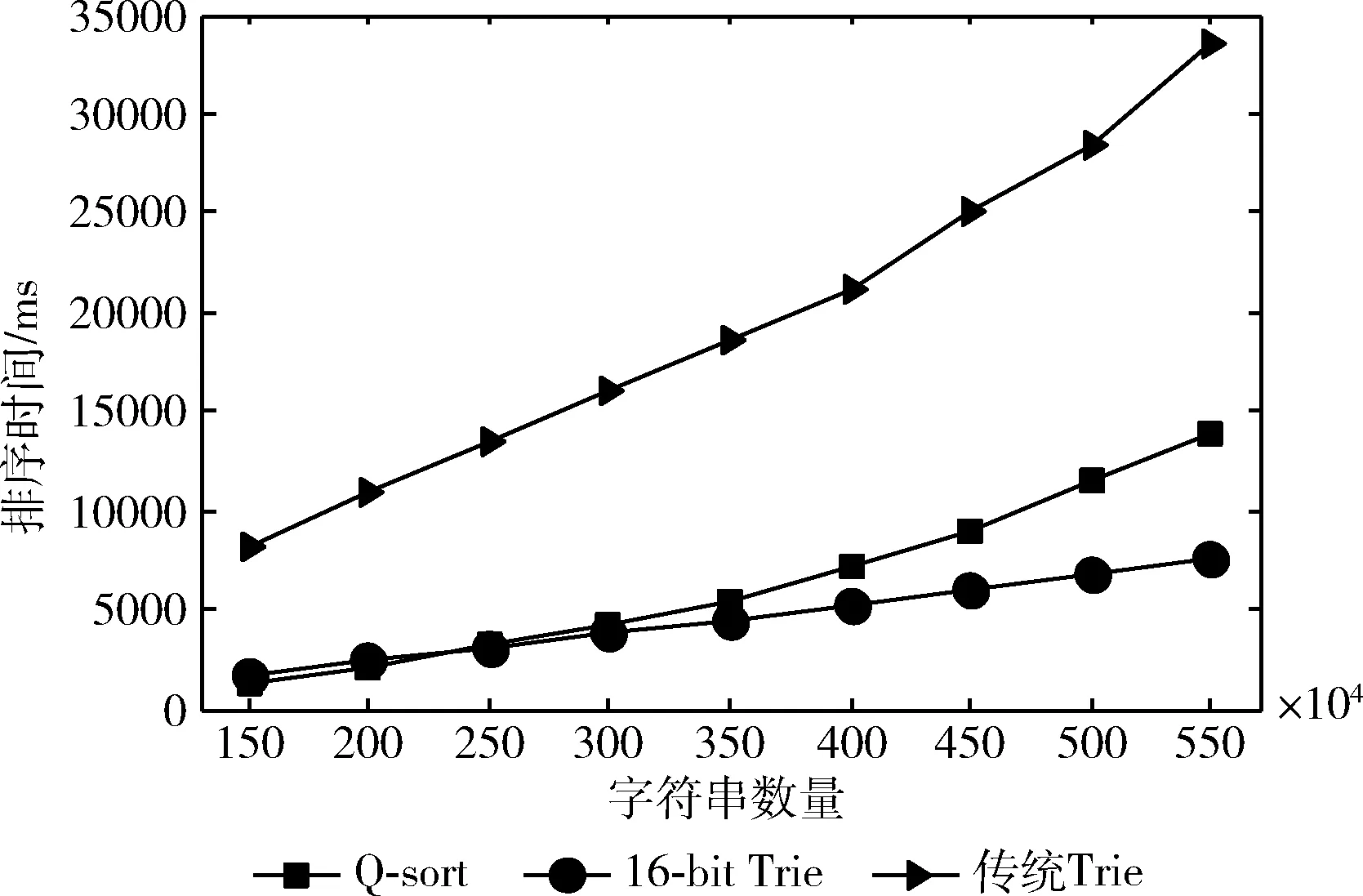
图7 定长数据的排序时间

从图7可见，16-bit Trie树的排序时间远低于传统Trie树的排序时间，这说明16-bit Trie树排序比传统Trie树通过遍历树完成排序的性能更好。传统Trie树不需要额外空间，通过遍历整个Trie树完成字典树排序，时间开销会很大。16-bit Trie树排序算法是在构建Trie树时借助邻近节点完成链表排序，不需要遍历大量节点，故而节省很多时间。而快速排序与16-bit Trie树排序的时间差值随着数据量的增加而增加，这说明16-bit Trie树排序算法在处理大规模动态数据时更具优势。相比快速排序，16-bit Trie树排序算法优势逐渐突显有两点原因:一是支持动态添加数据，当添加新数据时只需要对新增加的数据进行排序，而快速排序算法的排序时间随着数据量的增加而增加，这是因为当添加新数据时快速排序算法必须另辟一个能装下原始数据和新增加数据的大空间进行重排序；二是16-bit Trie树结构有公共前缀的特性，该特性减少了构建的节点数，必然节省排序时间。

以上测试发现另辟空间、重排序影响快速排序的时间性能，接下来，在相同数据量时测试排序次数对快速排序与16-bit Trie树排序的影响力。图8表示两种算法从初始50万数据量逐次增加50万至550万时使用一次排序和分两次进行排序的时间，曲线1是使用一次快速排序，曲线2是使用一次16-bit Trie树排序，曲线3是分两次进行快速排序，曲线4是分两次进行16-bit Trie树排序。如图8所示，随着数据量增加曲线1比曲线3耗时更少，快速排序算法使用一次快速排序比分两次进行排序用时更少，这说明另辟空间、重排序对快速排序算法有较大影响，重排次数越多排序耗时越多。而曲线2、曲线4基本重合，使用一次排序和分两次进行排序对16-bit Trie树排序算法基本没有影响，这表明数据动态增加对16-bit Trie树排序算法并无太大影响，16-bit Trie树排序算法支持动态添加数据。

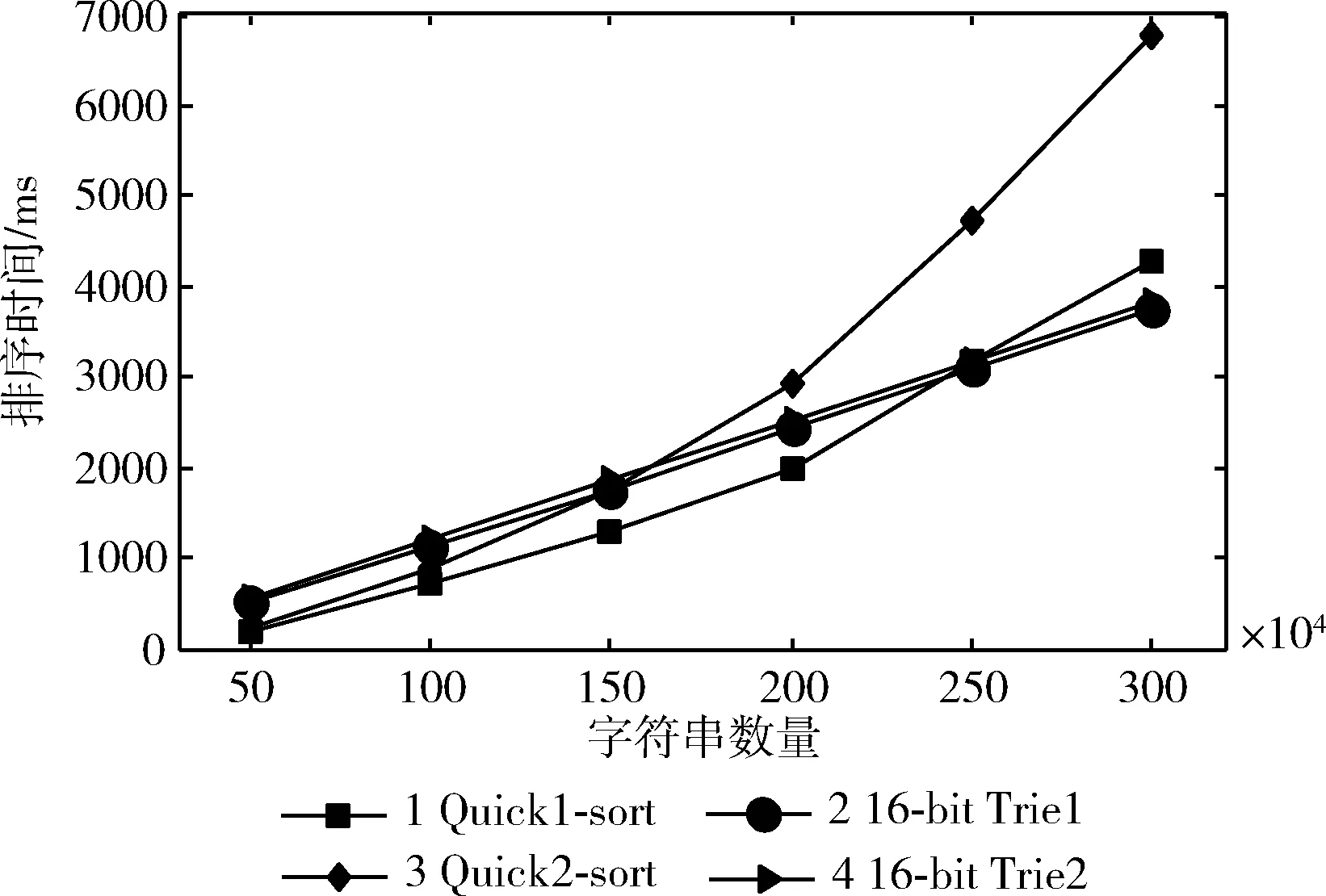
图8 使用一次快速排序和两次快速排序的排序时间

2.2 定量数据

图9是3种算法在初始100万数据量再动态增加20个数据的场景下数据长度为3-15字符时的排序时间。从图9可以看出，传统Trie树在数据长度为3-15字符时其排序时间随着字符长度的增加而增加，这是因为传统Trie树每增加一个字符，在构建和遍历Trie树时就需要多构建和遍历一个节点，故而随着字符长度的增加排序时间也逐渐增加。对于快速排序与16-bit Trie树排序，当数据长度为3-5字符时，两种算法的时间增幅都很大，但当数据长度为6-15字符时，16-bit Trie树排序算法基本没有增长趋势，快速排序算法有增长但增幅相比之前变小。在6-15字符范围内，增加数据长度并没有对16-bit Trie树排序算法产生很大影响，这是因为引入词缀压缩方法优化了16-bit Trie树结构，减少构建的节点数量，故而在数据量相同时增加数据长度并不会对排序时间产生较大影响。而快速排序算法在6-15字符范围内有增长但增幅变小，是因为使用前5个字符就可以区分100万数据量，故而在数据长度为6-15字符时增幅变小。

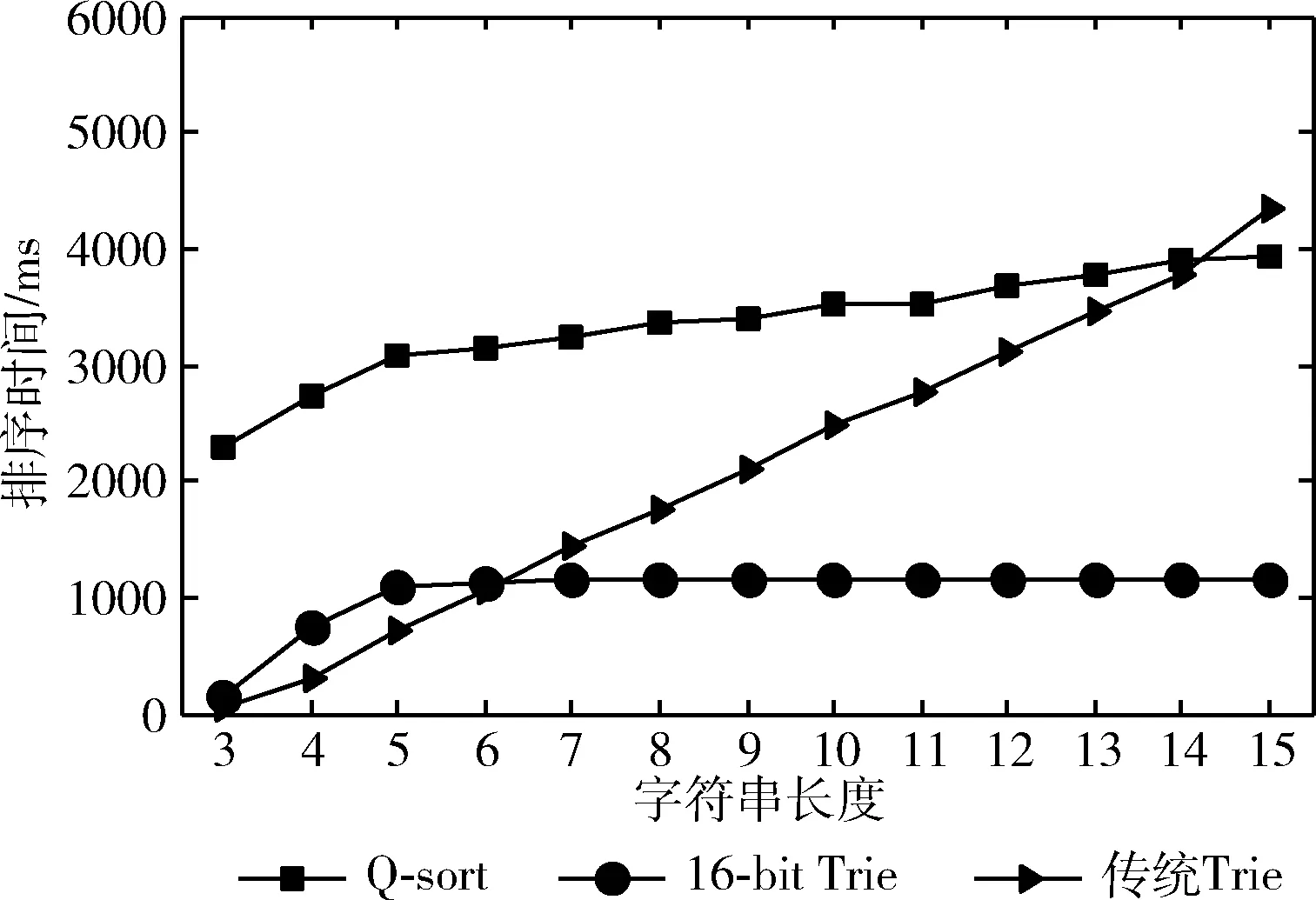
图9 定量数据的排序时间

从图9可以发现，在测试数据相同的情况下快速排序与16-bit Trie树排序的排序时间相差较大，快速排序算法耗时很多，是因为动态增加20个数据共进行20次快速排序，另辟空间、重排序使快速排序的时间开销很大，而16-bit Trie树排序算法直接对增加的20个数据进行排序，故而用时较少。

3 结束语

本文基于邻居节点提出了一种16-bit Trie树排序算法，该算法支持动态增加数据，引入了词缀压缩方法减少了构建的节点数，从而提高了整体排序速度。16-bit Trie树排序算法在构造16-bit Trie树时，使用动态数组存储子节点，避免了固定数组存储子节点时的空间浪费。

结果表明，相比其它两种算法，传统Trie树通过遍历整个Trie树完成字典树排序的时间开销最大；16-bit Trie树排序算法在数据动态增加时耗时最少，而快速排序在数据量较小时耗时较少，随着数据量的动态增加排序时间极速增加，这表明16-bit Trie树排序算法在处理大规模动态数据时更具优势。