基于深度学习的位置大数据统计发布与隐私保护方法

晏燕，丛一鸣，Adnan Mahmood，盛权政

（1.兰州理工大学计算机与通信学院，甘肃 兰州 730050；2.麦考瑞大学科学与工程学院，新南威尔士 2109）

0 引言

车联网、智能交通系统、移动众包、基于位置的服务（LBS,location-based service）系统、社交网络等热门应用的广泛兴起促使包含位置信息的数据与日激增，其规模和复杂性已经达到大数据的层次。位置大数据的统计发布可以为用户提供准确及时的交通和路况信息，帮助人们规划合理的出行时间和路线，获得高精度的LBS，同时有助于减少交通拥堵和不必要的资源浪费[1-2]。但是，对位置信息的不当发布和反向分析推理容易导致用户具体位置、运动轨迹、生活习惯、健康状况、兴趣爱好、经济条件等个人隐私的泄露，甚至可能危及用户财产和生命安全[3-5]。因此，解决位置大数据发布使用过程中的隐私保护问题，已经成为制约位置大数据应用发展最为迫切的任务。

按照一定时间间隔发布的位置大数据统计信息可供用户查询一定范围之内的其他用户数量、可搭乘的交通工具数量、车流状况等。这种位置大数据的统计划分发布过程依据特定的索引结构对二维空间进行划分和索引，并对索引区域内的位置点数量进行统计发布，减少了用户真实位置信息的泄露风险。通过对索引区域内真实位置点的统计值添加差分隐私噪声，还可以进一步提高发布位置统计数据的隐私保护效果。传统的位置大数据统计划分发布方法主要采用自顶向下的空间划分过程，构建网格或树型索引结构，并对各子区域迭代执行类似的划分策略，容易发生“过划分”或“欠划分”现象。划分结构的不合理增大了差分隐私统计发布的噪声误差和均匀假设误差，导致发布位置统计数据的查询精度降低。此外，迭代划分过程需要对位置信息集合进行多次扫描和划分停止条件判断，影响了数据发布方法的运行效率。

事实上，位置大数据的统计划分发布符合典型的时空序列特征。虽然个体用户的位置信息具有明显的随机性和动态变化特点，但是结合区域的统计结果来看，相邻发布时间间隔的位置大数据统计信息具有高度相关性，位置点密集的统计区域也存在一定的空间分布模式[6-7]。例如，在交通高峰期间，城市中的某些地区总是会发生交通拥堵现象并持续一段时间。近年来，基于深度学习的时空序列预测方法已经在交通流量和交通密度区域预测方面取得不少研究成果。因此，本文将深度学习引入位置大数据的发布过程，将历史位置大数据转换为深度学习模型可以分析和处理的划分结构时空序列，选用合理的深度学习模型挖掘和提取划分结构时空序列的特征，并实现位置大数据统计划分结构的有效预测。这对降低划分过程的冗余操作、提高数据发布方法的运行效率具有现实意义。本文的主要贡献如下。

1)提出二维空间位置大数据的网格划分和自底向上合并吸收算法，使最初与位置点分布无关的均匀网格划分结构转化为反映位置点分布密度的合理划分结构。

2)构建时空序列深度学习预测模型，通过提取历史位置大数据统计划分结构时空序列的潜在特征，实现对位置大数据统计划分结构的有效预测。

3)设计与预测划分结构相匹配的差分隐私预算分配和调整方案，并在不同数据规模的实际位置大数据集合上验证了所提方法在发布数据可用性和运行效率方面的优势。

1 相关工作

Dwork 等[8-9]提出的差分隐私模型通过向发布数据的统计结果添加随机噪声来实现隐私保护。因为具备严格的数学特性，该模型被认为是一种非常可靠的保护机制，并在数据发布隐私保护领域获得了广泛的应用。位置大数据统计划分发布的主要目标是在保证用户位置隐私安全的前提下，尽可能提供准确且高效的位置统计发布数据。但是，差分隐私噪声的添加和二维空间区域的均匀性假设问题，使位置大数据的统计划分发布结果与真实统计值之间存在一定误差。因此，二维空间划分结构的合理性是直接关系到位置大数据统计划分发布数据可用性的关键因素。

Qardaji 等[10]提出的均匀网格（UG,uniform grid）划分方法将二维空间均匀分割成众多网格，对网格区域内的位置点数量进行统计和加噪实现差分隐私保护，划分结构简单高效但是统计发布数据可用性不高。Xiong 等[11]使用等高线图来描述空间众包服务中的位置点分布，首先将全体空间区域划分为大量不相交的单元，然后将密度值相近的单元连接起来形成更大的区域。Wang 等[12]在UG 划分方法基础上利用线性回归方法得到网格划分粒度的最优解，采用基于桶排序的单元合并策略将所有相似网格进行合并，降低了统计发布结果中的噪声误差。文献[10]提出的自适应网格（AG,adaptive grid）划分方法在均匀网格划分的基础上对每个区域执行自适应网格划分，较好地反映了数据分布特性对划分结构的影响。张啸剑等[13]提出基于伯努利随机抽样技术的三层自适应网格划分发布方法，利用指数机制和高通滤波技术在划分结构的第二层过滤掉小于阈值的网格单元，对于大于阈值的网格单元继续进行划分，而对于小于阈值且相邻的网格单元则合并形成粗粒度的网格单元。Fanaeepour 等[14]利用欧拉特性和差分隐私来解决范围查询对空间区域数据的敏感性增加问题，使用用户区域大小和最小绝对偏差的约束推理来校准差分隐私保护的噪声。Wei 等[15]提出的位置隐私保护方案使用三层自适应网格划分发布方法和基于差分隐私的自适应完全金字塔网格算法，将移动众包服务中的确切位置拆分成含噪声的多级网格，从而实现位置隐私保护。Rodríguez 等[16]提出的空间分解算法借助粒子空间分布的统计信息提取最佳空间分解，使每个单元包括空间均匀分布的粒子。

树型结构具有更好的层次包含特性，可以提供更加便捷的空间范围查询服务。Cormode 等[17]使用与数据分布特性无关的完全四叉树对二维空间进行划分，并设计了几何隐私预算分配方法和后置调整方法，在一定程度上提升了范围计数查询的精度。吴英杰等[18]在完全四叉树划分的基础上根据设定的均匀性条件对划分结果进行自底向上的调整合并，从而降低均匀假设误差。Zhang 等[19]提出的PrivTree 划分发布方法引入一个可控的偏差来决定是否进行四叉树分割，消除了对预先定义四叉树划分深度的限制。Zhang 等[20]提出的PrivBayes 方法利用贝叶斯网络构建一组近似分布的低维子立方体，以发布合成数据集。针对空间众包服务中的位置隐私问题，Yang 等[21]根据工作人员的最大密度差将整个工作区域划分成4 个大小不同的子单元并递归调用这一过程，直至获得合理的空间结构。

一些划分发布方法将网格结构与树型结构有机结合，形成混合划分结构。Cormode 等[17]将依赖数据分布特性的kd 树结构和与数据分布无关的四叉树划分发布方法进行结合，有助于范围计数查询精度的进一步提升。文献[22]将AG 划分发布方法与kd树结构结合，将相邻的近似网格进行合并，以防网格划分过细而引入较多的噪声误差。Yan 等[23]提出的分层混合划分发布方法首先根据位置点的密度进行自适应网格划分，然后根据设置的高密度阈值和低密度阈值将网格分成3 种类型，对大于高密度阈值的网格进行自适应网格划分，对小于低密度阈值的网格停止划分，对处于2 种阈值之间的网格进行启发式四叉树划分，有效地提高了发布数据的可用性。Cai 等[24]将UG 划分发布方法和改进的H-tree划分发布方法相结合。张啸剑等[25]采用网格结构对空间数据区域进行均匀划分，通过四叉树对网格单元进行索引，提高了范围响应查询的精度。

针对传统划分发布方法难以确定空间分割停止条件、划分结构无法均衡噪声误差和均匀假设误差、数据扫描和迭代分析复杂等问题，本文借助深度学习模型对划分结构矩阵组成的时空序列进行时空关联分析，实现对位置大数据统计划分结构的有效预测和基于差分隐私保护的统计划分发布。

2 差分隐私模型

差分隐私模型与位置大数据统计划分发布具有天然的匹配性。位置大数据的连续动态变化使添加/删除某个位置点对整体位置数据分布特性的影响非常小，这一特质与差分隐私定义的内涵十分吻合。

定义1ε-差分隐私[8]。针对兄弟数据集T1和T2（T1与T2相比仅存在一条不同的记录）以及任意输出S⊆Range(K)，如果算法K在T1和T2上得到相同输出结果的概率满足

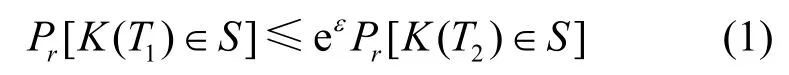
则称算法K满足ε-差分隐私。

式(1)中的ε称为隐私预算，其数值越小，算法K提供的隐私保护程度越高。因为攻击者即便获得了除特定目标记录之外的其他所有数据，依然无法根据查询结果推断该目标所对应的记录是否存在于原始数据集合中，从而实现了隐私保护。

定义2敏感度[26]。给定一个查询映射函数f，其敏感度Δf定义为该查询映射函数在兄弟数据集T1和T2上的输出之间的最大L1 范数距离

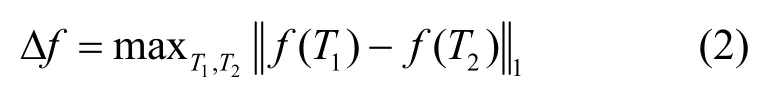
定义3Laplace 机制[26]。针对数值型数据，Laplace 机制通过向查询映射函数f的输出结果添加少量的独立噪声来实现差分隐私保护。用f(T)表示查询映射函数f作用于原始数据集T得到的结果，则 Laplace 机制返回的查询结果可以表示为K(T)=f(T)+η。其中η是满足Laplace 分布的连续型随机变量，其概率密度函数为

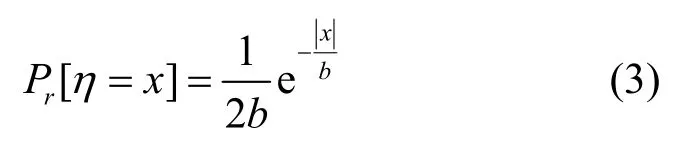
结合敏感度定义，添加的独立噪声服从幅度为b=Δf/ε的零均值Laplace 分布。

定理1串行组合特性[27]。对于一组随机算法{K1,K2,…,Kn}，其中Ki(1≤i≤n)满足对数据集T的εi-差分隐私，则该组随机算法{K1,K2,…,Kn}整体能够实现对数据集T的-差分隐私。

定理2并行组合特性[27]。如果数据集T可以划分为多个独立且互不相交的子集{T1,T2,…,Tn}，一组随机算法{K1,K2,…,Kn}分别作用于上述数据子集，其中Ki(1≤i≤n)满足对数据子集Ti的εi-差分隐私，则该组随机算法{K1,K2,…,Kn}能够实现对数据集T的max{εi}-差分隐私。

3 基于深度学习的划分发布结构预测方法

为了将深度学习应用于二维空间划分结构的预测，需要完成以下2 个关键步骤：首先是如何把二维空间分解问题转化为深度学习模型可以理解和分析的数据；其次是如何构造适当的数据结构并搭建合理的深度学习模型进行预测。

3.1 划分结构矩阵的形成

在实际应用中，不少交通量统计和LBS 应用系统都使用区域计数的方式发布位置大数据的统计信息。因此，本文首先根据位置大数据范围计数查询服务的最小尺度将位置信息覆盖的二维空间进行均匀网格划分，并统计每个网格区域内的位置点数量作为该网格的密度。为了解决均匀网格划分发布方法噪声误差和均匀假设误差较大的问题，根据局部分布均匀则整体也分布均匀的常理，采用自底向上合并吸收的策略对相邻的网格进行均匀性判断和合并操作，使最初与位置点分布无关的均匀网格划分结构转化为能够反映位置点分布密度的合理划分结构。

定义4区域合并条件。对于一个包含有m个网格的二维空间区域R，设Ci为每个网格的密度(i=1,2,…,m)，为区域R内的网格平均密度。若区域R中的统计值满足

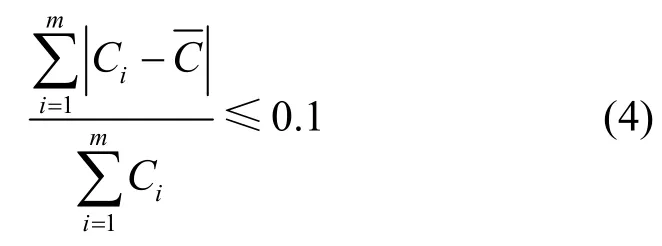
则区域R内的所有网格可以合并为一个区域。

定义4 要求区域R内的所有网格密度与整个区域的平均密度接近时才能进行网格合并操作，通过减小式(4)中的常数，可以进一步收紧网格区域合并的条件。

定义5划分结构矩阵。对于初始划分结构为N×N均匀网格的二维空间区域，可以构建如式(5)所示的矩阵以表示该二维空间区域的最终划分结构，其中的每一个元素hij(i,j=1,2,…,N)代表对应位置的网格区域所处的划分层次。hij的初始值设定为h(N=2h)，每当选定区域R内的所有网格满足合并条件时，对应的hij减小1，表示选定区域R发生一次区域合并。

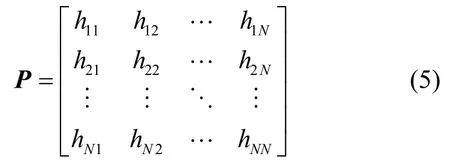
3.2 深度学习预测模型的构建

深度学习可以在大量复杂的非结构化数据中发现并自动提取隐藏在数据中的特征、类别、结构、概率分布等有价值的信息。在时间序列预测方面，递归神经网络（RNN,recursive neural network）[28]、长短期记忆（LSTM,long short-term memory）网络[29]、卷积神经网络（CNN,convolutional neural network）[30]等常用深度学习模型已经取得广泛的应用。RNN 可能随着时间的增大出现梯度消失或梯度爆炸的问题，并且其结构依赖于激活函数和网络参数。CNN可以有效地捕捉空间特性。LSTM 通过遗忘门决定丢弃或保留哪些信息，通过输入门更新细胞状态，因此在时间特征提取方面具有良好的效果。全连接长短期记忆（FC-LSTM,fully connected-LSTM）网络[31]被证明在处理时间相关性方面具有强大的功能，但是在处理时空数据时，其“输入-状态”和“状态-状态”的转换使用全连接，空间信息并没有被编码，所以在捕捉数据空间特性上的能力依然不足。

位置大数据的统计划分发布数据是由数据快照按照时间顺序串联形成的序列，符合典型的时空序列特征。为了实现对下一时刻位置大数据划分发布结构的准确预测，既要考虑时间上的相关性，又要考虑空间分布的相关性。卷积长短期记忆（ConvLSTM）模型[32]在“输入-状态”和“状态-状态”转换过程中都具有卷积结构，该模型的输入是三维张量，在加入卷积操作之后不仅能够得到时序关系，还能够像卷积层一样提取空间特征，非常适合时空序列的处理。图1 为ConvLSTM 模型结构。首先，通过遗忘门ft来决定要从细胞中丢弃的信息；然后，由输入门it中的tanh 层创建一个备选状态，并将其与输入门it信息进行矩阵对应元素相乘，上述两部分的结果相加确定了更新后的细胞状态Ct；最后，通过tanh处理的更新后的细胞状态与sigmoid门的输出进行矩阵对应元素相乘，得到最终的输出结果。式(6)～式(10)给出了ConvLSTM 的关键方程，其中，*表示卷积算子，◦表示Hadamard 积。

图1 ConvLSTM 模型结构

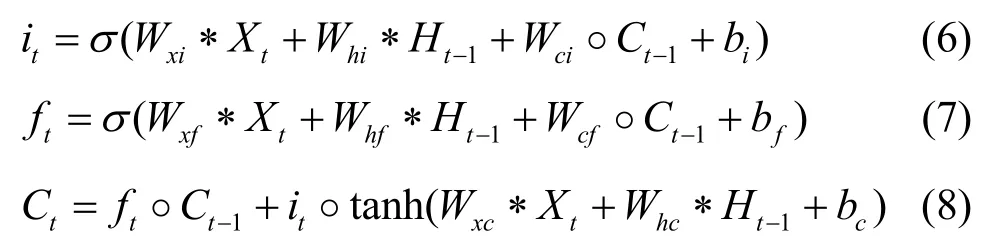
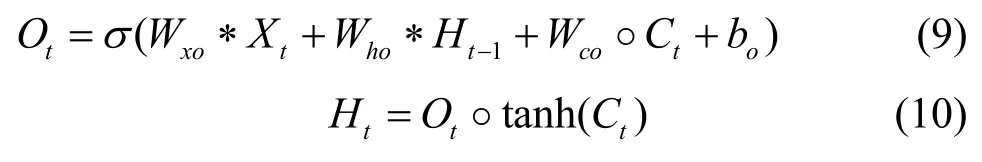
时空长短期记忆（ST-LSTM）模型[33]在LSTM模型的基础上加入了时空单元，可以把时间特征和空间特征保存到每个时刻的细胞状态，从而获得其时空关系。图2 为ST-LSTM 模型结构，输入门it确定进入细胞的新序列，遗忘门ft选择保留多少历史序列信息于细胞中。当前细胞输入Xt经过由权重矩阵和偏置形成的LSTM 结构后输出的结果，与上一层的时空门输出结果STt-1相耦合，用于融合序列间的相互影响。每个序列的各个特征通过这种方式进行重构，从而实现空间信息之间的依赖。式(11)和式(12)给出了ST-LSTM 模型的时空门STt和细胞状态Ct的计算式。

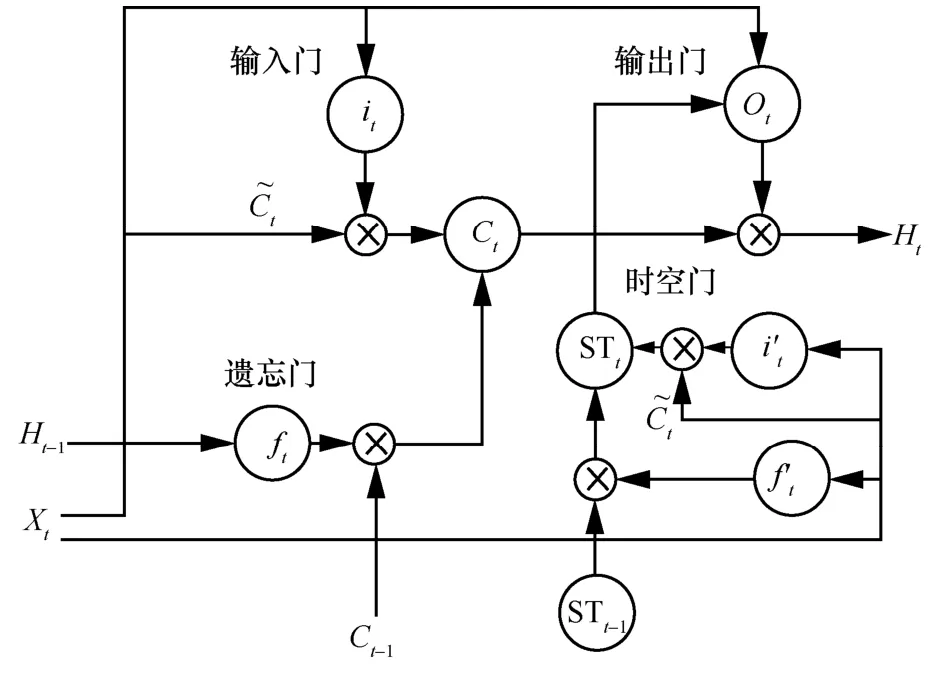
图2 ST-LSTM 模型结构

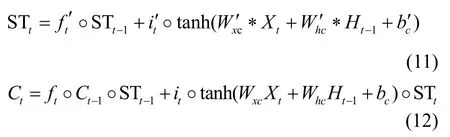
本文分别以 LSTM、CNN、ConvLSTM、ST-LSTM 模型为核心，构建位置大数据划分结构时空序列的深度学习预测模型。首先使用算法1 将历史位置大数据集合转换为划分结构矩阵；然后按照时间顺序把划分结构矩阵组织成三维时空序列，并将其作为深度预测模型的输入张量，实现划分结构矩阵的有效预测。4 种模型的具体参数如表1～表4所示。

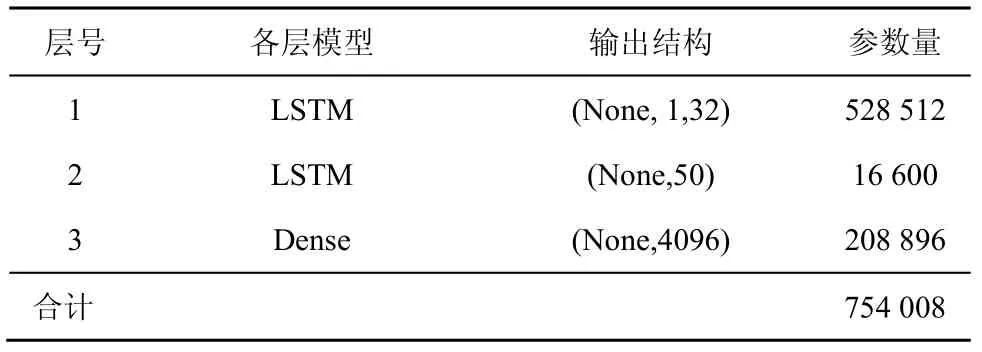
表1 LSTM 预测模型参数

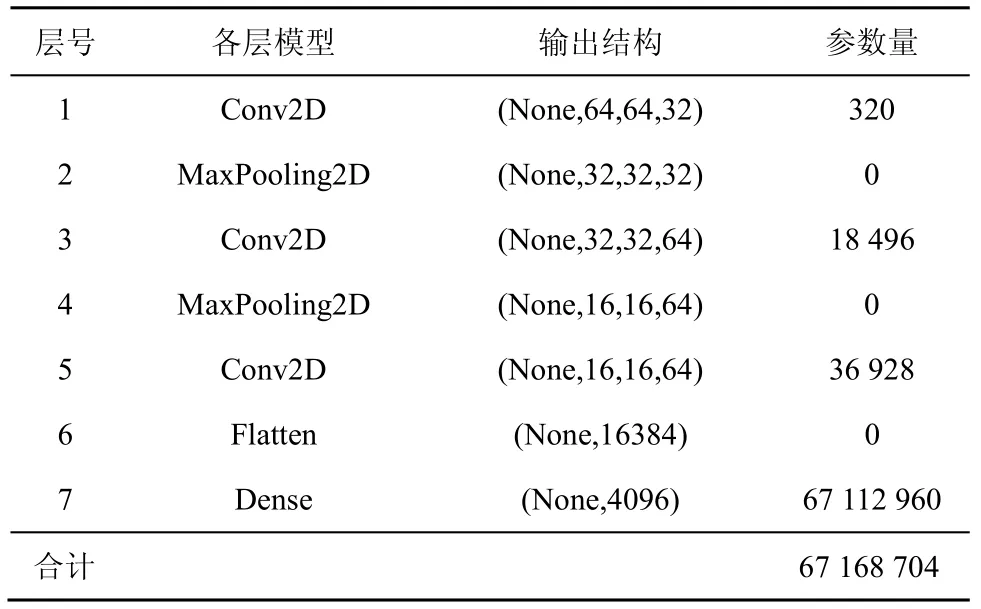
表2 CNN 预测模型参数

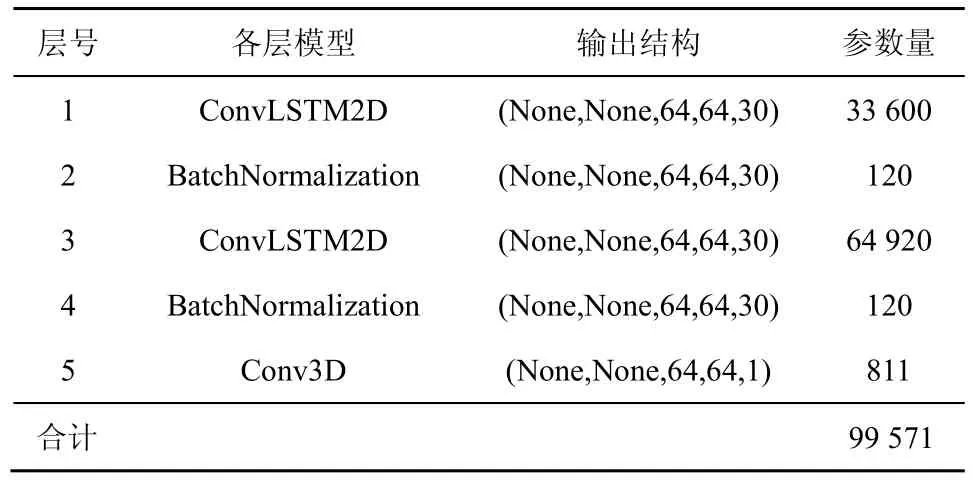
表3 ConvLSTM 预测模型参数

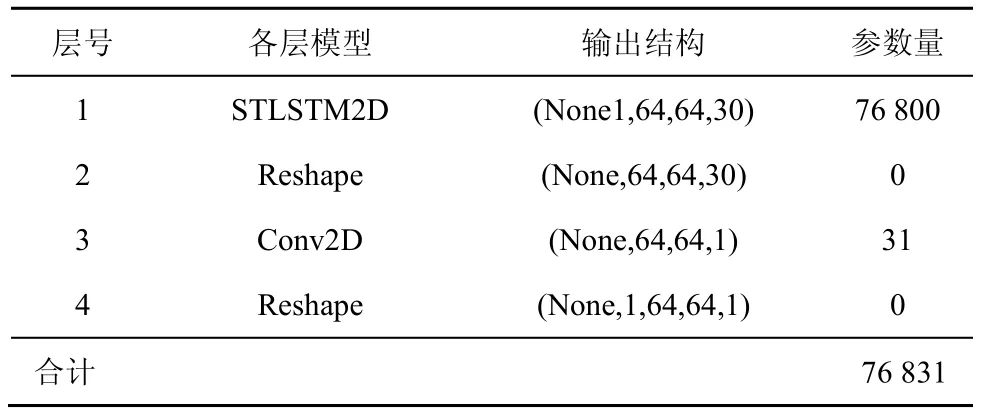
表4 ST-LSTM 预测模型参数

4 基于差分隐私的位置大数据统计划分发布

为了实现对位置大数据统计发布信息的隐私保护，需要结合空间划分结构进行差分隐私预算分配，并对各空间区域的统计结果添加扰动噪声。差分隐私预算分配的相关研究[34-38]指出，随着划分层次的增加，自顶向下逐步增大各层的隐私预算有助于降低噪声方差，提高统计发布位置信息的范围计数查询精度。因此，本文设计了差分隐私预算的梯度分配方法，并结合划分结构的不平衡特点进行隐私预算的调整，实现满足ε-差分隐私的位置大数据统计划分发布。

定义6隐私预算梯度分配。假设差分隐私总预算为ε，对于深度为h的层次化空间划分结构，每一层分配的差分隐私预算为

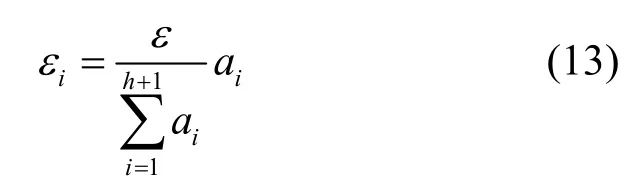
其中，ai=i(i-1)/2(i=1,2,…,h+1)是一个公差逐渐增大的序列，ε1是分配给根节点（即整个位置数据集覆盖的二维空间）的隐私预算值，εh+1是叶子节点（即初始网格划分区域）的隐私预算值。

定义7隐私预算调整。在深度为h的层次化空间划分结构中，如果发生网格合并的区域处于划分层次i，则按照式(14)调整该区域的差分隐私预算

以图3 所示的自底向上合并吸收结构为例，其中灰色节点表示未发生网格合并的区域，可以根据式(13)分配相应的差分隐私预算；黑色节点表示发生了网格合并的区域，需要按照式(14)进行差分隐私预算调整。当i=3 时，发生网格合并的区域隐私预算应当调整为；当i=2 时，，从而保证任意从叶子节点到达根节点的路径都满足=ε。

图3 差分隐私预算调整示意

算法2 给出了差分隐私位置大数据统计划分发布方法的具体过程。图4 描述了本文基于深度学习的位置大数据统计发布与隐私保护方法的整体流程。

图4 位置大数据深度学习预测和差分隐私统计划分发布流程

推论1算法2 能够为位置大数据统计划分发布结果提供ε-差分隐私保护。

证明位置大数据的统计划分发布主要向用户提供范围计数查询服务。关于用户提交的任意查询范围Q，存在以下3 种情况。

1)Q所覆盖的查询范围完全包含在划分发布结构的单个区域范围之内。根据算法1，Q可能被包含在初始网格区域或者是合并网格形成的区域内。对于前者，差分隐私总预算ε按照式(13)为每一层划分节点分配隐私预算，从初始网格区域自底向上到达根节点的路径满足差分隐私。对于后者，假设该区域位于划分发布结构的第l层(l=2,3,…,h)，根据本文提出的隐私预算调整策略，该区域的隐私预算强度为；从该区域自底向上到达根节点的路径满足差分隐私。因此，情况1)的查询范围Q之内发布数据受到强度为εQ=ε的差分隐私保护。

2)Q所覆盖的查询范围包含划分发布结构中的p个完整区域。根据位置信息的空间分布，划分发布结构将位置集合所覆盖的二维空间分割为独立且互不相交的若干个区域。根据定理2，查询范围Q之内的发布数据受到强度为εQ=max{εp}的差分隐私保护。p个完整区域既可能是初始网格区域，也可能是合并网格形成的区域，根据情况1)可知∀εp=ε，所以情况2)的查询范围Q内发布数据受到强度为εQ=max{εp}=ε的差分隐私保护。

3)Q所覆盖的查询范围包含p个完整区域并与q个区域相交。类似于情况2)，此时查询范围Q之内的发布数据受到强度为εQ=max{εi}(i∈p∪q)的差分隐私保护。根据情况1)可知∀εi=ε，所以该情况下查询范围Q之内发布数据受到强度为εQ=max{εi}=ε的差分隐私保护。

综合上述情况可知，算法2 能够为位置大数据统计划分发布结果提供ε-差分隐私保护。

5 实验与分析

为了对本文基于深度学习的位置大数据统计发布与隐私保护方法进行综合评估和分析，从划分发布结构的合理性、深度学习预测模型的准确性、发布位置大数据的可用性、数据发布方法的运行效率等方面，将本文方法与经典的UG 方法[10]、AG方法[10]、Quad-opt 方法[17]、Unbalanced Quadtree方法[39]进行比较分析。

实验数据分别选用纽约市共享单车使用记录数据集 BikeShare（2015—2017 年）、Macquarie University 智慧城市项目的车辆统计数据集Macquarie Park、纽约出租车管理委员会提供的乘车记录数据集Yellow_tripdata（2009—2016 年）。实验平台选用华为云服务器ECS（pi2.4xlarge.4：Intel SkyLake 6151 3.0 GHz/Intel Cascade Lake 6278 2.6 GHz CPU；GPU：2×NVIDIA T4/2×16 G；64 GB 内存；100 G SSD 云硬盘；Windows Server 2016 64 位标准版镜像），算法使用Python 3.8 编程，采用深度学习框架TensorFlow 作为后端引擎，选择Keras 高层神经网络API 作为前端搭建深度学习预测模型。

5.1 划分发布结构的合理性

为了直观地了解位置大数据统计划分发布结构的合理性，对相同位置大数据集合的空间分布状态和各种方法得到的划分发布结构进行横向比较。图5 是各种方法针对Yellow_tripdata 数据集得到的划分发布结构。其中UG 方法的常数参量c=10，AG 方法的隐私分配比例α=0.5，Quad-opt 方法的划分深度h=6，Unbalanced Quadtree 方法的均匀性判定阈值θ=0.01。

观察图5 中的各种划分结果不难发现，UG 方法得到的划分结构与位置数据集合的分布状态无关，划分结构中存在大量的空网格（密度值为0 的网格），添加Laplace 噪声之后容易产生较大的噪声误差，影响位置统计信息的可用性。AG 方法的划分过程是对UG 方法中密度较大的网格区域进一步划分细粒度的网格单元，其效果是对位置点密集区域进行与数据分布特性相关的细致划分，但是仍然无法避免位置点稀疏区域存在的噪声误差问题。Quad-opt 方法的划分过程采用与位置数据分布状态无关的完全四叉树结构，当划分层次较少时容易产生较大的均匀假设误差，而当划分层次较多时与UG 方法同样存在较大的噪声误差。Unbalanced Quadtree 方法采用基于均匀性判断的非平衡四叉树划分结构，可以根据位置数据的分布状态启发式的引导划分过程，其合理性高于前3 种方法。本文方法能够根据位置大数据的分布特性对二维空间进行细致划分和自底向上的合并，细致划分降低了位置点密集区域的均匀假设误差，自底向上合并过程减少了位置点稀疏区域的“过划分”现象，避免过多的噪声误差。综合比较上述划分发布结构，对于相同的位置大数据集合，本文方法产生的统计划分发布结构更加合理。

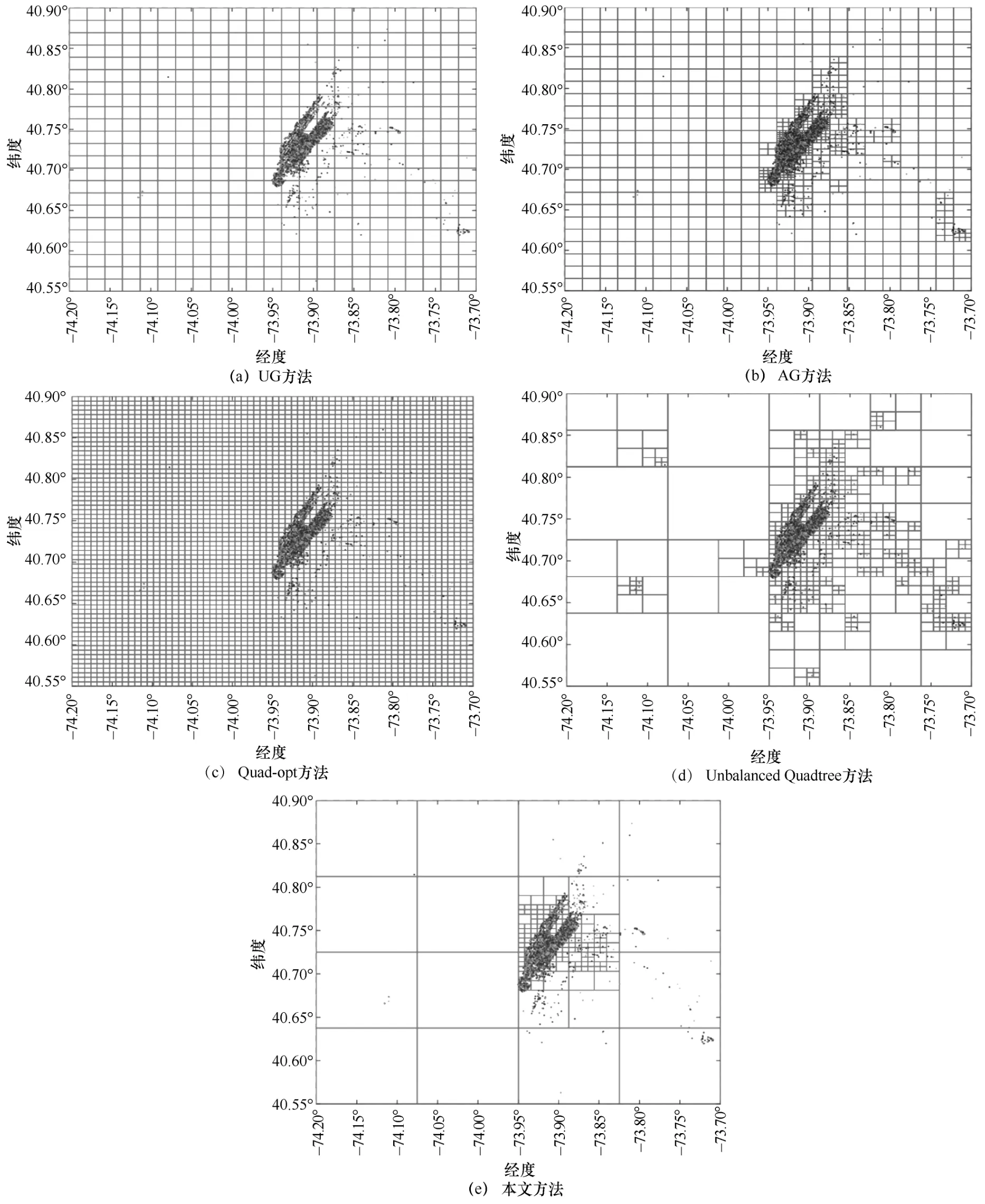
图5 划分发布结构比较

5.2 深度学习模型预测准确性

为了验证深度学习模型对划分发布结构预测的准确性，首先将实际位置大数据集合按照发布时间间隔进行子集划分（BikeShare 数据集的发布间隔为 Δt1=60min，Macquarie Park 数据集的发布间隔为 Δt2=15min，Yellow_tripdata 数据集的发布间隔为 Δt3=10min），并按照本文提出的网格划分与合并方法生成划分结构矩阵；然后按照时间顺序将划分结构矩阵组织成深度学习预测模型的输入序列，对下一发布时刻的划分发布结构进行预测；最后与真实数据子集上的划分结构矩阵进行比较。

使用均方误差（MSE,mean square error）、均方根误差（RMSE,root mean square error）、平均绝对误差（MAE,mean absolute error）评估深度学习预测模型的准确性，定义如式(15)～式(17)所示。其中Fp表示划分结构矩阵的预测值，Ft表示划分结构矩阵的真实值。

引入多分类评价指标中的宏平均（Macro-average）和微平均（Micro-average），进一步衡量预测划分结构矩阵与真实划分结构矩阵在所有网格区域划分结果上的误差，其定义如式(18)～式(19)所示。其中TP（true positive）、FP（false positive）、TN（true negative）和FN（false negative）分别表示真正例数、假正例数、真反例数和假反例数，F1 函数的定义与多分类评价一致。

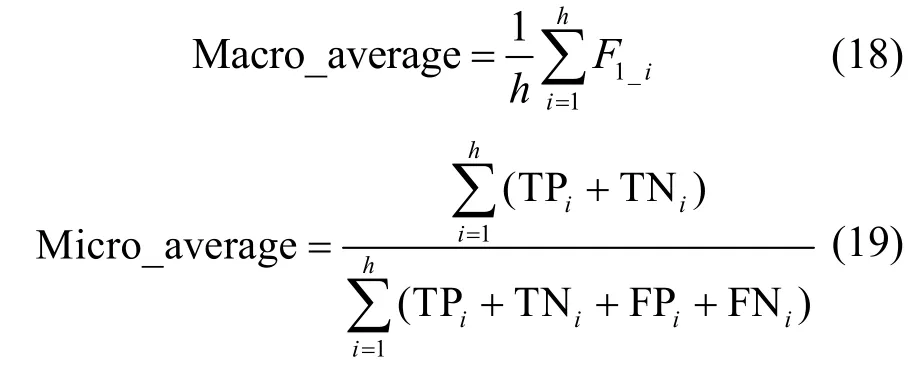
实验过程中各类深度学习预测模型的结构和参数设置如表1～表4 所示，各模型的准确性评价指标结果如表5 所示。在不同规模的位置大数据集合上，基于时空特性的深度学习预测模型均获得了较低的预测误差。特别是在预测划分层次与真实划分层次之间的误差方面，基于时空特性的深度学习预测模型的宏平均值和微平均值远高于简单时间序列模型的预测精度，说明利用深度学习预测模型得到的统计划分发布结构在绝大多数情况下都获得了与真实划分结构一致的结果，证明了深度学习预测模型的可行性和准确性。

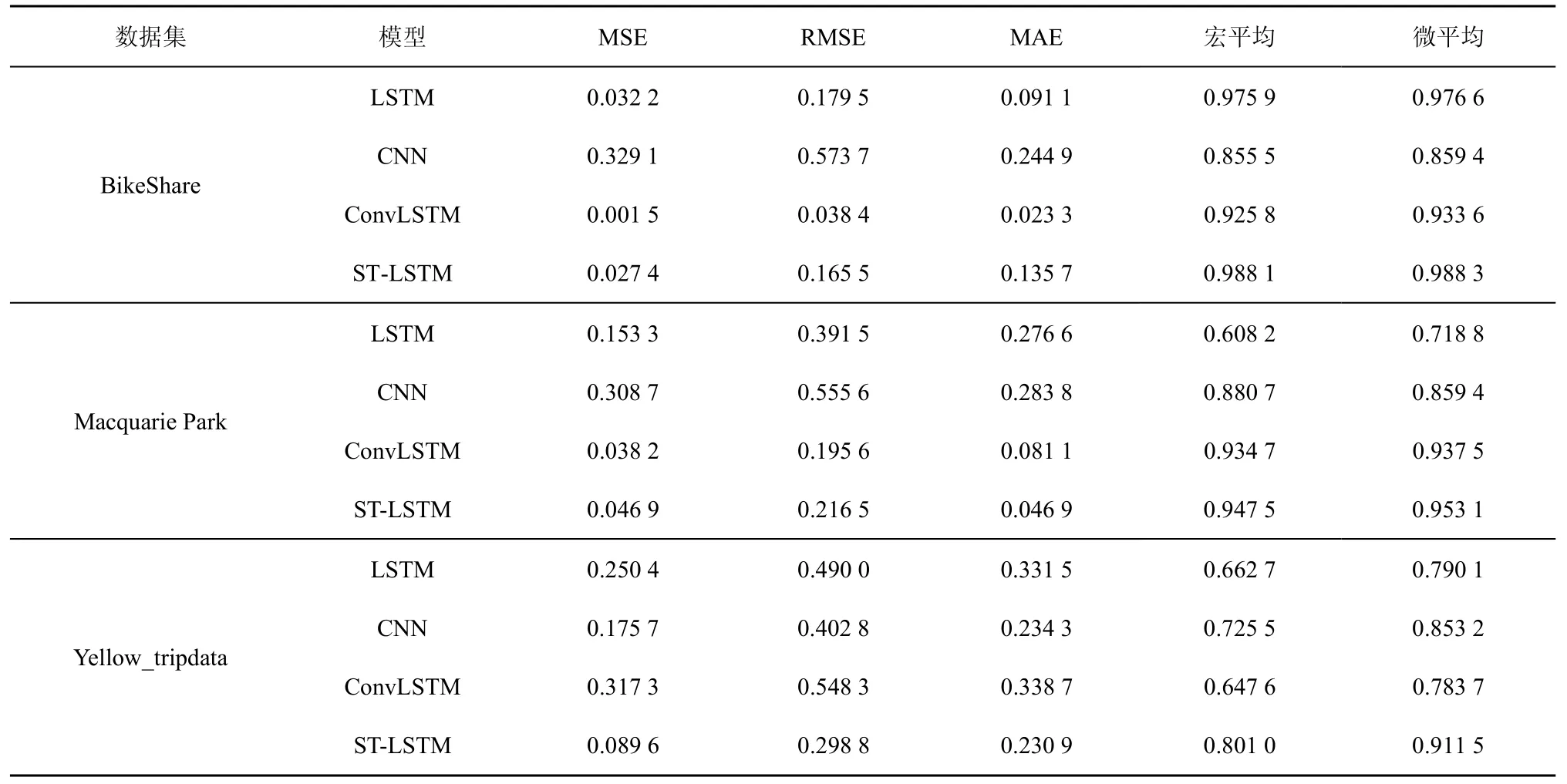
表5 各模型的准确性评价指标结果

5.3 发布位置大数据的可用性

为了验证本文位置大数据统计划分发布数据的可用性，选用5.2 节中效果最好的ST-LSTM 模型实现位置大数据划分发布结构预测，按照算法2 实现差分隐私位置大数据统计信息发布。针对发布结果进行不同尺寸的范围计数查询，并将本文方法的相对误差与UG、AG、Quad-opt、Unbalanced Quadtree 等方法的结果进行比较。实验过程中范围计数查询区域的尺寸设置如表6 所示，各种方法的参数设置与5.1 节相同，差分隐私模型分别添加隐私预算为ε=0.1、ε=0.5、ε=1的Laplace 噪声，每种类型的查询区域随机生成1 000 个。相对误差的定义如式(20)所示。

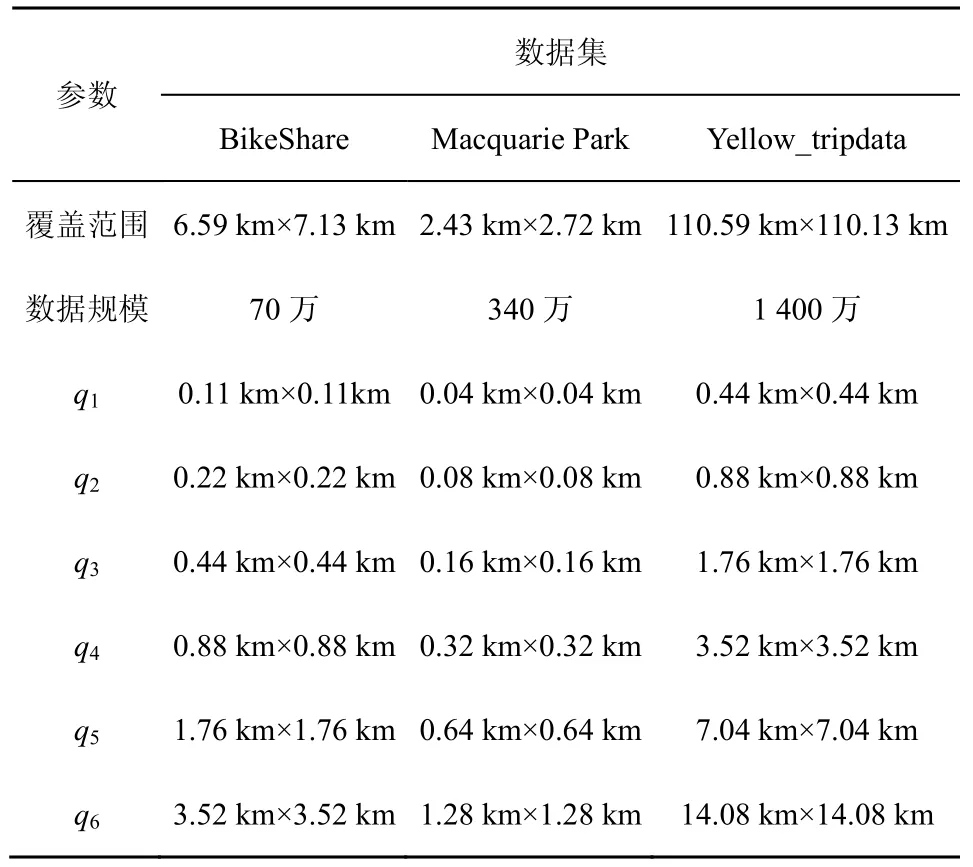
表6 实验过程中范围计数查询区域的尺寸设置

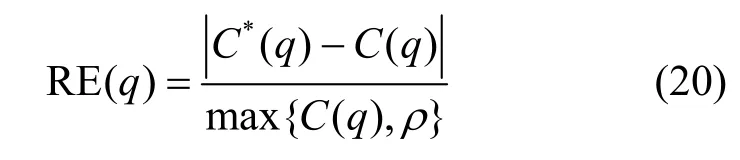
其中，q是用户向位置大数据统计发布平台提交的查询范围，C(q)是在原始位置大数据集上相应范围内得到的查询结果，C*(q)是在发布位置大数据集上相应范围内得到的查询结果，代表位置大数据集的大小。

图6～图8 用对数坐标展示了各种方法在不同数据集上的相对误差比较结果。在相同的实验数据集上，各种方法的相对误差都随着隐私预算ε的增大而逐渐减小，其原因是隐私预算ε的增大使添加的Laplace 噪声值减小，因而发布数据与真实统计值之间的误差也减小了。在数据分布较稀疏的BikeShare 和Macquarie Park 数据集上，UG 和Quad-opt 方法的相对误差较大，其原因在于UG 和Quad-opt 方法的粗粒度划分过程与位置点分布密度无关，导致在较小查询范围内的区域噪声误差较大，而在较大查询范围内的均匀假设误差较大。AG方法对位置点密集区域进行了第二层细粒度的网格划分，因此在查询范围较小时相对误差较小，而当查询范围尺度较大时相对误差发生恶化。Unbalanced Quadtree 方法根据区域分布密度进行启发式四叉树划分，本文方法根据均匀性进行自底向上的网格合并，得到的划分结构比UG、AG 和Quad-opt 方法更合理，因此在各类查询范围下的相对误差都优于上述算法。在数据分布最稠密的Yellow_tripdata 数据集上，AG 方法的第二层细粒度网格划分使在查询范围较小的情况下（q1和q2）获得了较低的相对误差，而当查询范围增大时，本文方法的范围计数查询精度最高。

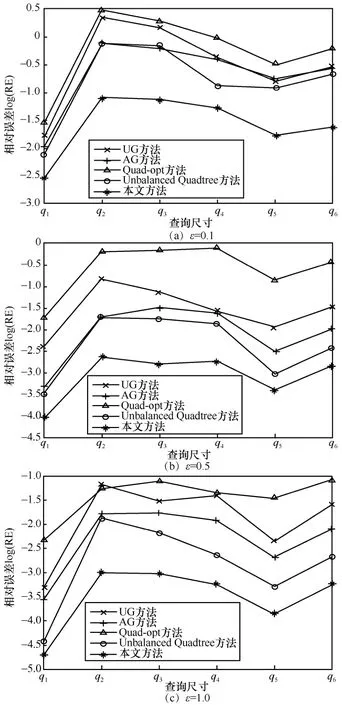
图6 BikeShare 数据集范围计数查询精度比较

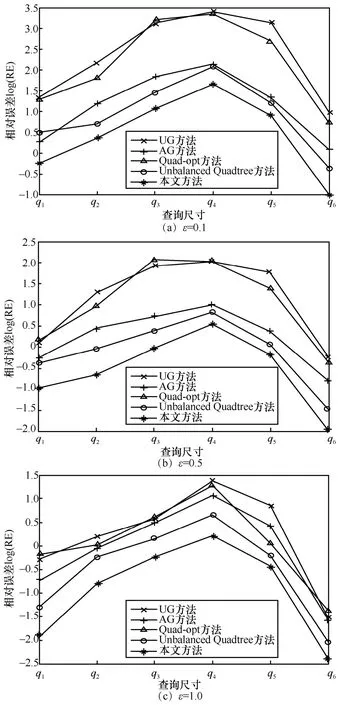
图7 Macquarie Park 数据集范围计数查询精度比较

图8 Yellow_tripdata 数据集范围计数查询精度比较

5.4 位置大数据发布方法的运行效率

为了验证本文提出的差分隐私位置大数据统计划分发布方法的运行效率，将本文方法的整体运行时间与UG、AG、Quad-opt、Unbalanced Quadtree等方法进行比较分析，各种方法的参数设置与5.2 节相同。由于差分隐私预算强度对统计划分发布方法的运行时间没有明显影响，本文以ε=0.5为例对3 个不同规模的实际位置大数据集进行实验比较。图9用对数坐标展示了各种位置大数据统计划分发布方法在实际位置大数据集合上的运行时间。

从图9 可以看出，UG 方法由于不考虑位置数据的具体分布状态所以运行效率最高，而且几乎不受数据集合大小的影响。AG 方法在UG 方法的基础上多执行了一遍细粒度网格划分，所以整体算法用时长于UG 方法。Quad-opt 方法的划分过程虽然也不考虑位置数据的具体分布状态，但是采用深度优先遍历的树型迭代过程，整体用时明显高于UG 和AG 方法。Unbalanced Quadtree 方法划分过程需要结合位置数据的具体分布状态，但是因为能够在位置点稀疏区域避免不必要的细致划分，反而节省了不少时间，整体运行时间介于AG 和Quad-opt 方法之间。本文方法使用深度学习预测模型产生统计划分发布结构，深度学习预测模型的构建、训练、参数优化等步骤可以借助历史数据提前完成，所以在运行时只需花费极少的时间产生预测划分结构，继而添加差分隐私噪声形成位置大数据的统计划分发布结果，整体的运行时间仅次于UG 方法。

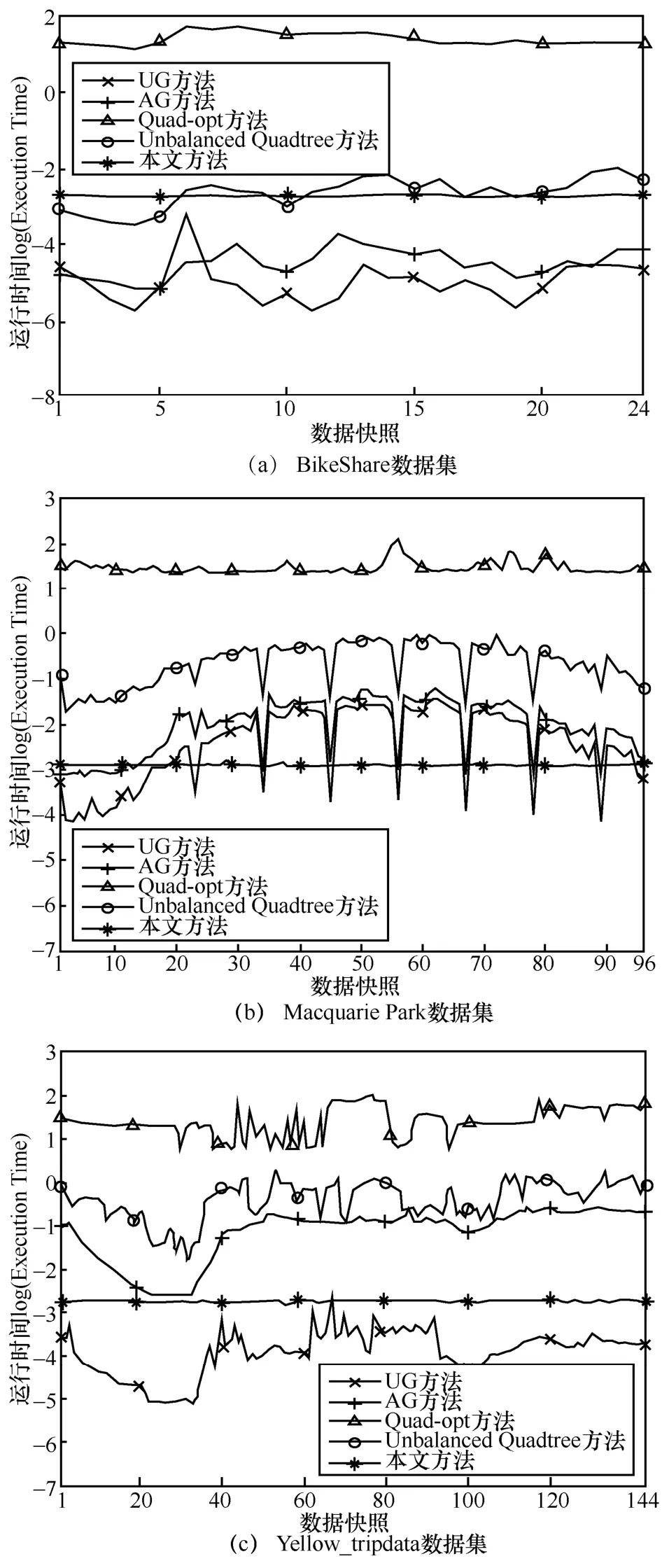
图9 不同数据集的运行时间比较

6 结束语

大数据技术的深入发展和移动智能终端的广泛普及使基于位置的各种服务与用户的工作和生活紧密相关，涉及的位置隐私保护问题也引起了广泛的关注。位置大数据统计划分发布技术借助空间分解和差分隐私保护模型实现位置数据统计信息的发布，在保证数据可用性的基础上有效避免了用户位置隐私的泄露风险。为了充分利用位置大数据的周期性和时空关联性，减少统计划分过程的冗余操作，本文提出基于深度学习的位置大数据划分结构预测方法和差分隐私发布方法。通过设计合理的网格划分与合并算法将历史位置大数据的划分结构转换为三维时空序列。构建基于时空序列的深度学习预测模型，通过提取历史位置大数据统计划分结构矩阵的时间和空间相关特性，实现对划分结构矩阵的有效预测。设计了与预测划分结构相匹配的差分隐私预算分配和调整方案，实现了位置大数据统计划分发布结果的差分隐私保护。通过实际位置大数据集合的实验和分析证明了本文方法的可行性和有效性。