基于载波相位的高精度室内快速定位算法

范绍帅，荣志强，田辉，李立华

（北京邮电大学网络与交换技术国家重点实验室，北京 100876）

0 引言

随着5G 时代的到来以及无线终端的不断普及，基于位置信息服务（LBS,location-based service）与人们日常生活的联系日益紧密。可靠的LBS 基于精准的位置信息，而精准的位置信息由高精度定位技术获取。因此，高精度定位技术成为近年来定位领域的热点问题。目前，基于全球导航卫星系统（GNSS,global navigation satellite system）的定位技术已经趋于成熟，在大多数室外定位场景中可以为用户提供稳定可靠的位置信息，精度可达亚米级。与室外定位场景不同，室内定位场景较复杂。随着城市建设的不断发展，包括大型工厂、大型商业中心、大型办公楼等在内的复杂建筑物与日俱增。建筑物的墙体会造成卫星信号的遮挡，建筑物的结构和其中的物品则会引起复杂的多径效应。除了定位场景不同，室内定位精度的需求远远高于室外定位。已经冻结的5G Release 16 标准要求在室内室外精准定位场景中，定位技术的定位精度需求为米级[1]。考虑到定位技术与工业物联网等应用的结合，未来Release 17 标准将进一步将室内定位精度提升至厘米级[2]。在智能制造领域，位置信息主要用来提升生产效率及供应链管理，对工具防错以此提高产品质量。智能制造领域的许多应用都需要高精度位置信息，对定位精度有较高要求，精度在厘米级[3]。车辆高精度定位是实现智慧交通和自动驾驶的必要条件。在一些高级的驾驶业务中，如自动驾驶、远程驾驶和编队驾驶中，稳定的厘米级定位是其安全可靠服务的必要保障[4]。

目前，主流的室内定位技术，包括射频识别（RFID,radio frequency identification）定位技术[5]、超宽带（UWB,ultra wide band）定位技术[6]、超声波定位技术[7]和雷达定位技术[8]等，已经在特定环境下得到了应用，但是它们往往需要额外的设施部署，导致建设成本较高。在智能制造等典型应用场景中，大量的高速移动机器人、自动导引车（AGV,automated guided vehicle）、可移动装配平台和可移动装配材料工具等移动设备都需要接入现有的蜂窝移动通信系统来完成高可靠低时延通信。结合已部署的网络进行定位技术，包括基于到达时间（TOA,time of arrival）[9]、到达时间差（TDOA,time difference of arrival）[10]、到达角度（AOA,angle of arrival）[11]和接收信号强度（RSSI,received signal strength indicator）[12]等定位技术，不需要额外部署，但是定位精度不高，只能达到米级。将载波相位测量应用于现有蜂窝通信系统中可以解决上述成本和精度的问题。载波相位最早由文献[13]提出独立应用于蜂窝系统，并成为3GPP Release 17 及Release 18的备选定位技术。该技术将系统中传输连续的参考信号作为载波相位定位参考信号（C-PRS,carrier phase positioning reference signal），支持终端基于C-PRS 进行载波相位测量。在整周模糊度解算准确的情况下，载波相位可以进行精准的测距。文献[13]指出将载波相位测量应用到定位中有可能达到亚米级甚至厘米级定位精度。在室内无线环境中，除了信号的多径效应和噪声会影响定位精度外，设备之间的钟差也是一个重要因素。文献[14]证明了基于TDOA 的定位算法的均方误差随着钟差的L2 范数而增加，文献[15]证明了钟差会在载波相位定位的测量值引入误差项，从而影响定位结果。现有的室内定位算法往往忽略钟差对定位精度的影响，或者事先对钟差进行估计。例如，文献[16-17]采用凸优化的方法来估计钟差，但估计残差仍对定位精度有明显的影响。因此，在实际应用中钟差的消除对于高精度定位是十分必要的。

此外，实时定位是室内定位的一个典型应用领域，在实际中有着广泛的应用，如查找定位室内的资产、追踪定位人员、远程监控等[18]。以上应用都要求室内定位技术在保证定位精度的条件下可以对待定位目标的位置进行快速响应，即快速解算出位置信息。当前，已有大量研究人员在该领域取得丰硕的研究成果。文献[19]提出了一种基于AOA 的室内实时定位方法，该系统利用Wi-Fi 信号的多载波特性在天线和数据包较少的情况下快速估计信号的AOA，保证了定位的实时性。文献[20]设计了一种利用智能天线的实时定位系统，该系统利用智能天线接收的信号强度进行定位，避免了离线阶段密集型数据库的建立，提高了效率。上述研究虽然保证了定位的实时性，但是定位精度都在米级，难以满足愈发严苛的精度要求。文献[21]提出了一种基于载波相位测量的高精度定位算法，该算法基于多个时间点的测量数据，可以对整周模糊度进行解算，进而实现高精度定位。该算法可以达到亚米级甚至厘米级的定位精度，前提是累积足够数量采样时间点的测量数据。对于实时定位中的应用场景，短时间内往往不能提供足够多的测量数据，导致该算法在实际应用中存在局限性。因此，设计可以兼顾定位精度和解算速度的定位算法具有重要的现实意义。

基于上述考虑，本文提出了一种基于载波相位的高精度室内快速定位算法。

本文主要研究工作如下。

1)引入参考终端消除设备间钟差对定位算法的影响。具体来说，结合移动终端及参考终端的测量值，利用TDOA 差分测量和载波相位双差测量消除设备间钟差的影响。

2)利用锁相环（PLL,phase lock loop）不失锁期间整周模糊度不变的特性，设计了一种结合多时间点测量数据的整周迭代解算算法，该算法可以加速整周模糊度的解算，进而缩短定位所需的时间。

3)在消除设备间钟差和结合多时间点测量数据迭代解算整周模糊度的基础上，提出了一种基于载波相位的高精度室内快速定位算法。

4)仿真结果表明，本文所提基于载波相位的高精度室内快速定位算法可以完全消除设备间钟差对定位的影响，在短时间内精确解算整周模糊度，实现高精度的三维定位。当存在周跳残余时，本文所提基于载波相位的高精度定位算法依然可以保持比较高的定位精度。

1 系统模型

1.1 定位场景

本文所提基于载波相位的高精度室内快速定位算法的定位场景设定在一个室内三维空间内，其中有M个位置已知的固定无线接入点，编号分别为1,2,…,M，位置坐标为ui=(xi,yi,zi)T，i=1,2,…,M。将编号为1 的无线接入点设为参考无线接入点，其他无线接入点分别结合其测量值来获取相应的TDOA值。除了无线接入点外，三维空间内还有2 个终端，一个是移动终端s，位置未知，在t时刻的坐标为，可以在三维空间内随机移动；另一个是参考终端r，位置已知且固定，坐标为u(r)=(x(r),y(r),z(r))T。假设在定位过程中，2 个终端始终可以与各个无线接入点进行直接通信。各个无线接入点可以接收2 个终端发射频率为fc的C-PRS信号[13]，并观测接收信号的TOA 值和载波相位值。

1.2 TDOA 测距模型

在t时刻，编号为i（i=1,2,…,M）的无线接入点收到移动终端s发射的连续信号并观测得到TOA值为

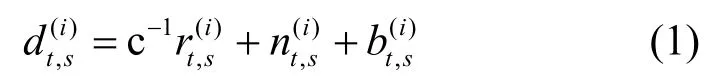
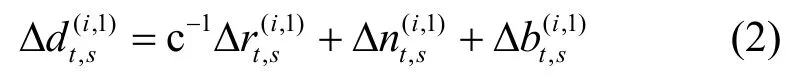
其中，Δ(·)(i,1)=(·)(i)-(·)(1)。同理，参考终端r的TDOA 观测值可以表示为

编号为2,3,…,M的无线接入点在t时刻分别结合参考无线接入点的测量值获取相应的TDOA 观测值。这里将它们统一表示成向量的形式

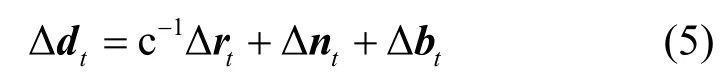
1.3 载波相位测量模型

载波相位测距常应用于GNSS 中，由于载波相位信号的周期性，信号接收机只能观测到一个小于一个周期的相位φr，称为相位的残余部分，而相位的整数倍周期部分2πN未知，其中N为整周模糊度。真实的相位可以表示为

想要得到真实的相位，就需要精确地解算整周模糊度N。在观测初期，信号接收机观测到相位的残余部分φr，同时锁相环或者锁频环（FLL,frequency lock loop）对载波相位的跟踪进行锁定，随着时间的变化，信号发射机和信号接收机之间的距离可能会发生变化，这意味着真实相位可能发生变化，只要锁相环或者锁频环不失锁，信号接收机在初期观测的整周模糊度N就保持不变，真实相位的变化量体现在相位残余部分[22]。移动终端s在t时刻观测到来自编号为i的无线接入点的载波相位信号的相位可以表示为

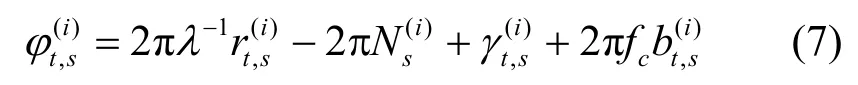
2 算法描述

2.1 消除钟差

从式(2)和式(7)可以看出，TDOA 观测值和载波相位观测值都存在钟差。为了消除设备间的钟差对定位精度带来的影响，本文所提基于载波相位的高精度定位算法引入了位置已知的固定参考终端r。对于TDOA 观测值，考虑编号为1 的参考无线接入点、编号为i的无线接入点、移动终端s以及参考终端r，将式(2)和式(3)做差可得TDOA 差分测量值或TOA 双差测量值

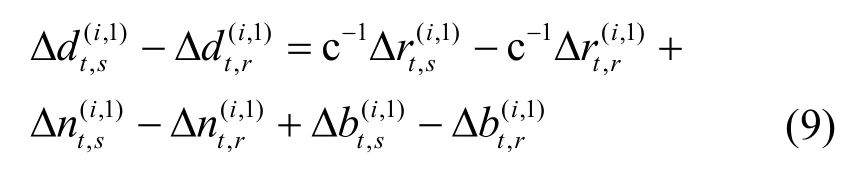
由于参考终端r的位置已知，因此为已知量。根据式(4)可知=0，将所有已知量移到等式左边可得移动终端s消除钟差之后的TDOA 观测值为

对于载波相位观测值，考虑编号为1 的参考无线接入点、编号为i的无线接入点、移动终端s，将做差可得载波相位单差测量值

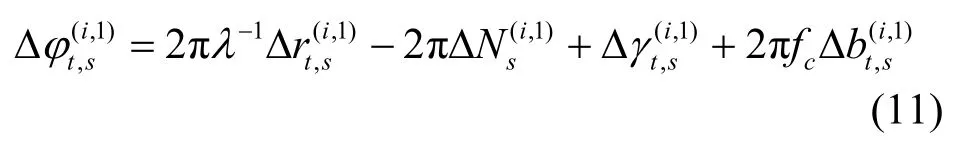
同理，对于参考终端r有载波相位单差测量值

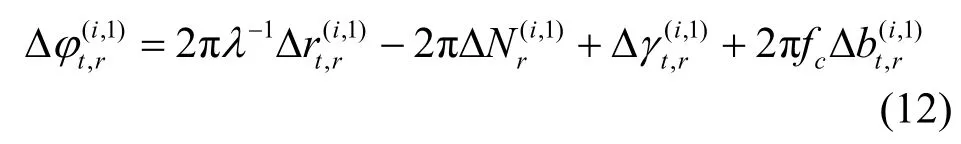
将式(11)和式(12)做差可得载波相位双差测量值

其中，Δ(·)s,r=(·)s-(·)r，，为4 次（2 个无线接入点分别观测终端s和终端r的载波相位）载波相位测量误差方差的和。与TOA 测量同理，在消除钟差的同时引入了更大的测量方差。由于，因此=0，将已知量移到等式左边可得双差方程

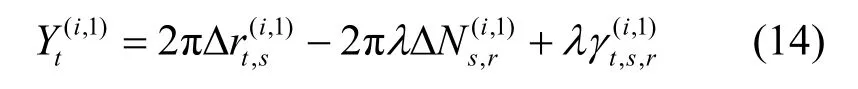
2.2 基于多时间点的整周迭代解算算法

载波相位测距比TDOA 测距具有更高的精度，那么应用载波相位测距得到的距离信息进行定位可以取得更高的定位精度。载波相位高精度测距的关键在于整周模糊度N的精确解算。观察式(14)可知，除了未知的双差整周模糊度和双差测量误差之外，还存在未知量，将展开可得

将TDOA 测距模型中观测得到的TDOA 向量Δdt代入传统的TDOA 定位算法（如Chan 算法[24]）得到一个t时刻关于移动终端s的粗定位结果ut,p。限于TDOA 的测距精度和三维定位场景，粗定位结果ut,p的定位精度往往不能达到很高的定位精度。

假设在第k-1 轮次迭代的结果为ut,k-1=(xt,k-1,yt,k-1,zt,k-1)T，将式(15)在ut,k-1上进行泰勒展开，从而达到线性化方程的目的，展开形式如下

将式(16)代入式(14)得到泰勒展开方程，并将i分别等于2,3,…,M得到的泰勒展开方程组成方程组，形式如下

其中，bk=-2π(||ui-ut,k-1||-||u1-ut,k-1||)，Gk=[Ut,-λE(M-1)(M-1)]，Ut为泰勒展开系数矩阵，E(M-1)(M-1)是规模为M-1的单位矩阵，ΔX=[xt,k-xt,k-1,yt,k-yt,k-1,zt,k-zt,k-1,。

方程组(17)有唯一解的必要条件是方程数量≥未知数的数量。方程组(17)中的方程数量是M-1，未知数的数量为3+M-1，不满足上述条件，所以方程组(17)显然没有唯一解。为了解决这一维度问题，假设锁相环或者锁频环在n（n≥2）个时间点上不失锁，即整周模糊度N保持不变，将n个时间点上（t,t+1,…,t+n-1）的双差方程组成如式(17)所示的方程组，则方程组(17)中元素更新为，，Z是规模为（M-1）×3 的零矩阵，ΔX=[xt,k-xt,k-1,yt,k-yt,k-1,zt,k-zt,k-1,…,zt+n-1,k-zt+n-1,k-1,。运用加权最小二乘法求解方程组(17)可以得到

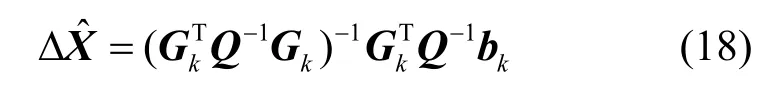
其中，Q为测量误差的协方差矩阵。通过

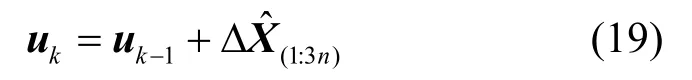
可得第k轮迭代的结果uk，其中中前3n个元素组成的向量。将uk作为泰勒展开点继续进行迭代，以此类推，直至解算结果收敛。本文所提基于多时间点的整周迭代解算算法流程如图1所示。

图1 整周迭代解算算法流程

2.3 最终定位

当解算出整周模糊度的浮动解后再利用LAMBDA（least-square ambiguity decorrelation adjustment method）算法[25]求得整周模糊度的固定解。这里的整周模糊度固定解为双差整周模糊度，按照式(20)可以修正相位差并计算出距离差。

将距离差代入传统TDOA 定位算法即可解算出最终的位置估计uf。

3 仿真分析

仿真定位场景设定在一个三维空间内，如图2 所示。三维空间的长L=100 m，宽W=20 m，高H=10 m，参考终端r位置已知且固定于房间正中间，移动终端s可以在房间内随机移动，2 个终端始终在各个无线接入点的通信范围内，所有无线接入点及参考终端的坐标均在图2 中标出。在仿真中，所用信号载频fc为3.5 GHz，无线接入点数量M=6，光速c=3×108m/s。

图2 仿真场景

3.1 一般场景下算法性能仿真分析

为了验证所提算法对整周模糊度解算的加速效果，仿真实验分为两部分：该算法与自身的对比实验以及该算法与现有相关算法的对比实验。

在与自身的对比实验中，相同的仿真场景下，设置迭代组和非迭代组的对比实验来验证本文所提基于多时间点的整周迭代解算算法对整周模糊度解算的加速效果。两组实验分别在不同数量的采样时间点上进行多次位置估计，并计算位置估计的均方根误差来量化定位精度。两组实验的流程除整周模糊度的解算部分不同外，其余均相同。针对整周模糊度解算部分，迭代组采用本文所提基于多时间点的整周迭代解算算法解算整周模糊度浮动解，而非迭代组只使用方程组(17)一次解算的结果作为整周模糊度的估计值，即方程组(17)在代入初始迭代点ut,0（ut,0为传统TDOA 算法估计的位置）之后进行一次解算的结果中的整周模糊度部分作为整周模糊度浮动解。不同采样时间点数上算法的性能如图3 所示，从迭代组的仿真曲线可以看出，当采样时间点数n取不同值时，本文所提基于载波相位的高精度定位算法的性能不同。随着n的增大，位置估计的均方根误差变小，算法的定位精度变高，注意，这里n需不小于4，这是因为当无线接入点数量M=6，采样时间点数n＜4 时，方程组(17)为欠定方程组或者迭代结果无法收敛，鉴于相关算法在采样时间点数n=4 时均方根误差的仿真结果大概在几十米量级，为了更好地展示对比效果，图3 从采样时间点数n=5 开始。通过对比迭代组和非迭代组的曲线可以看出，在相同测量标准差下，迭代组在采样时间点n=5 时位置估计的均方根误差小于非迭代组在采样时间点n=50 时位置估计的均方根误差。本文所提算法相对于非迭代的解算算法在达到更好的精度效果时可以使用更少采样时间点的测量数据，这说明本文所提算法可以加速整周模糊度的解算，进而缩短定位所需时间。

图3 不同采样时间点数上算法的性能

在与现有相关算法的对比实验中，相同仿真场景下，与文献[21]中所提算法进行对比。分别在不同数量的采样时间点上进行多次位置估计，并计算位置估计的均方根误差来量化定位精度。仿真结果如图3 所示，通过对比迭代组和相关算法的曲线可以看出，在相同测量标准差下，迭代组在采样时间点数n=10 时位置估计的均方根误差和相关算法在采样时间点数n=50 时位置估计的均方根误差相当。在达到相同的定位精度性能的同时，本文所提算法相对于现有相关算法可以使用更少采样时间点的测量数据，这说明本文所提基于载波相位的高精度室内快速定位算法可以在短时间内实现高精度定位。

图4 为不同误差标准差下的整周模糊度收敛情况。仿真中，采样时间点数n=4，误差标准差分别取不同值，整周模糊度残差由计算。

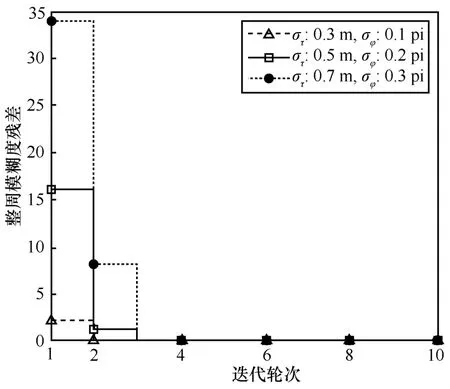
图4 不同误差标准差下的整周模糊度收敛情况

如图4 所示，本文所提基于多时间点的整周迭代解算算法的整周模糊度解算结果在不同的误差标准差下均能收敛。为了证明本文所提算法的整周模糊度解算结果在不同采样时间点上均能收敛，表1 统计了不同误差标准差及不同采样时间点下本文所提算法解算结果收敛所需迭代轮次，将算法分别仿真1 000 次，求得迭代轮次后进行求和平均。从表1 中可以看出，在不同的仿真场景下，本文所提基于多时间点的整周迭代解算算法的整周模糊度解算结果均能在4 次以内得到收敛。

表1 不同误差标准差和不同采样时间点下所需平均迭代轮次

除了采样时间点数n之外，TOA 距离标准差和载波相位测量标准差也是影响算法性能的重要因素。固定采样时间点数n，分别分析不同的TOA距离标准差和不同的载波相位测量标准差对本文所提基于载波相位的高精度定位算法的整体性能的影响。图5 为不同误差标准差下所提算法的位置估计的性能对比。从图5 中可以看出，当载波相位测量标准差不变时，仅改变TOA 距离标准差，3 条累积概率分布曲线几乎重合为一条线。因为TOA 距离标准差只会影响迭代算法初始点的精度，随着迭代算法的进行，迭代的结果将会收敛于真实值，对整周模糊度浮动解的解算影响不大。而当TOA 距离标准差不变时，随着载波相位测量标准差的增大，算法精度性能下降，这是因为载波相位测量误差量存在于方程组中，不能在迭代过程中消除或者减小其影响。

图5 不同误差标准差下所提算法的位置估计的性能对比

为了验证本文提出的钟差消除方法对钟差的消除效果，将本文所提基于载波相位的高精度定位算法在无线接入点间存在钟差和无线接入点间完美同步2 种情景下分别仿真并进行定位精度性能对比。假设设备之间的钟差在0～50 ns上均匀分布，仿真结果如图6 所示，从图6 中可以看出，当测量标准差一定时，2 种情景下绝对误差的累积概率分布曲线重合，当测量标准差不同时，2 种情景下绝对误差的累积概率分布曲线均重合。这说明在不同的测量标准差条件下通过引入参考终端都可以完全消除设备间钟差对定位精度的影响。

图6 有无钟差条件的所提算法的性能对比

图7 为本文所提基于载波相位的高精度定位算法与传统TDOA 定位算法的性能对比。如图7所示，在相同的TDOA 测量标准差下，所提算法的定位误差有90%的概率在0.07 m 内，而传统TDOA 定位算法的定位误差则在3.56 m 内，前者显著优于后者2 个数量级。当减小传统TDOA 定位算法的测量标准差时，所提算法仍然优于传统TDOA 定位算法。这说明本文所提基于载波相位的高精度定位算法相比于传统定位算法具有很高的定位精度优势。

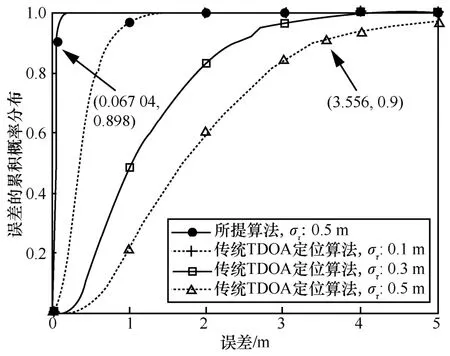
图7 所提算法与传统TDOA 定位算法的性能对比

3.2 考虑周跳残余场景下性能仿真分析

在获取载波相位观测值时，无线接入点需要始终保持对载波相位参考信号的跟踪。由于室内信号传播环境比较复杂，多径效应、物体的遮挡以及信号的干扰都可能使接收信号产生短暂中断，从而导致观测相位的整周数产生跳变，上述现象称为周跳。周跳发生后，无线接入点可以恢复对载波相位定位参考信号的跟踪观测，使观测结果中相位的小数部分不受影响，但是整数部分发生跳变，从而导致载波相位的整体观测结果发生错误。在连续观测载波相位的系统中，周跳不仅会影响当前时刻的载波相位观测值，同样将影响该时刻之后的载波相位观测值。

在基于载波相位的高精度定位算法中，周跳往往是影响定位精度的一个重要因素，因此，周跳的检测与修复是十分必要的。在现有的研究中，很多周跳检测与修复算法[26-30]已经被提出。本文所提基于多时间点的整周迭代解算算法可以利用现有的周跳检测与修复算法对周跳进行处理。例如，利用多个采样时间点上的载波相位观测值的高次差[30]可以实现周跳的检测与修复，即确定周跳发生的时刻以及估计周跳的大小并对整周部分进行补偿。但由于虚警概率的存在，现有的周跳检测与修复算法有时不能完美修复周跳，偶尔存在少量的周跳残余，即未完美修复的周跳以及未检测到的周跳。

下面给出存在周跳残余情况下本文所提基于载波相位的高精度定位算法的仿真，以验证存在周跳残余下该算法的性能。参照文献[25-28]中的关于周跳残余的描述，假设在50 个采样时间点上随机2 个采样时刻存在周跳残余，周跳残余大小在[-5,+5]中的非零整数离散值上均匀分布，TOA 距离标准差为0.5 m，载波相位测量标准差为0.2 pi。图8 为采样时间点分别取25 和45 下，是否存在周跳残余下所提算法位置估计的性能对比。

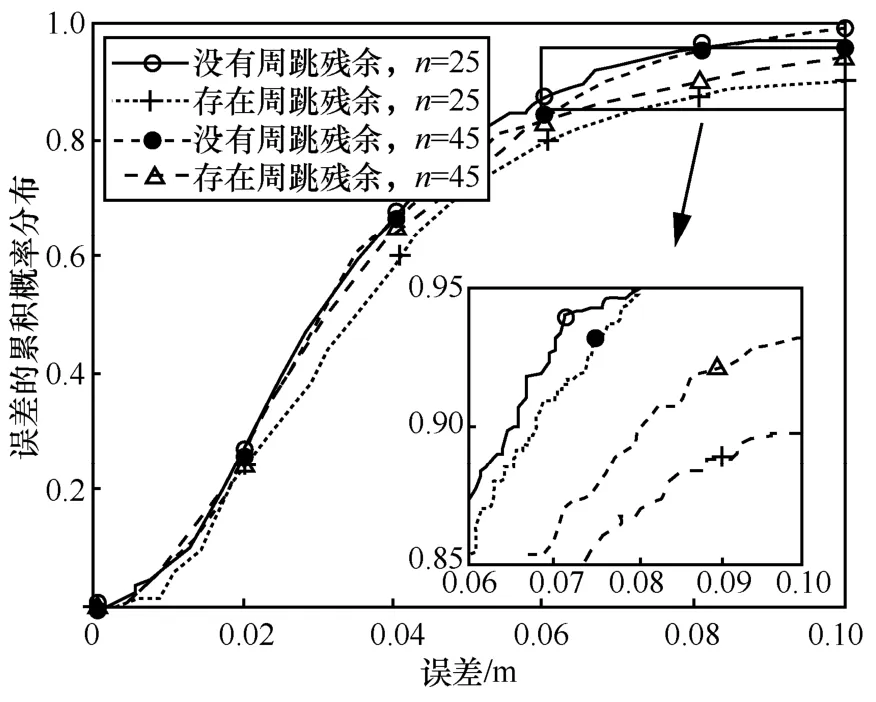
图8 是否存在周跳下所提算法位置估计的性能对比

图9 为是否存在周跳对不同采样时间点上算法性能的影响。从图9 中可以看出，存在周跳残余和没有周跳残余下所提算法的CDF 曲线非常接近，这说明本文所提算法在存在周跳残余的情况下依然能保持很高的定位精度。在图9 中，周跳残余存在于随机的2 个采样时刻，存在周跳残余下本文所提算法位置估计的RMSE 在某些采样时间点上相对于没有周跳残余下算法的RMSE 略有升高，但是依然保持良好的定位性能。

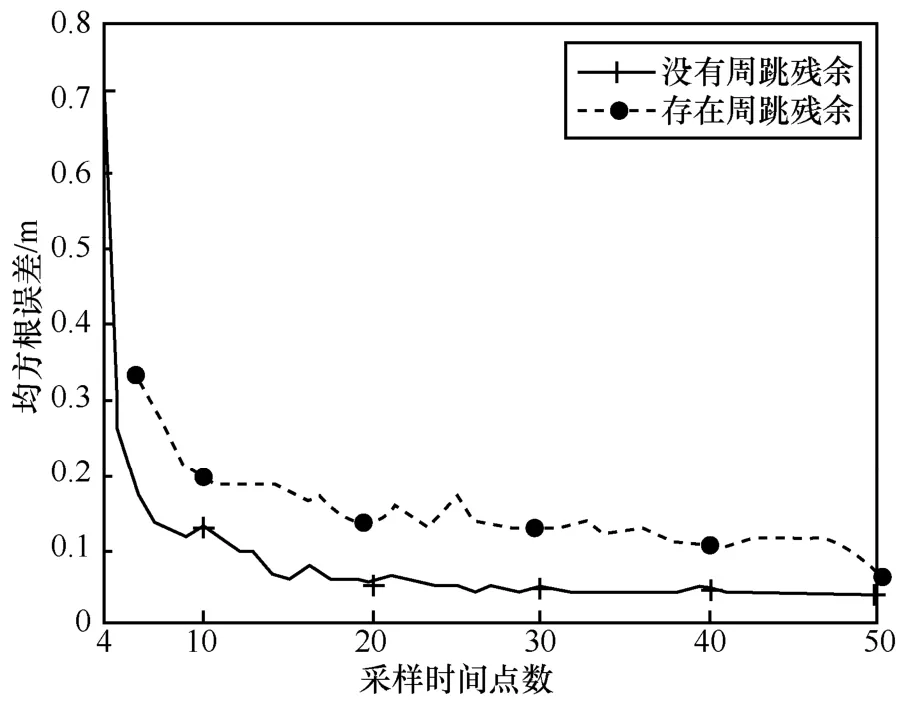
图9 是否存在周跳对不同采样时间点上算法性能的影响

4 结束语

本文分析了室内无线环境影响定位算法的因素，提出一种基于载波相位的高精度室内快速定位算法。考虑到设备间的钟差会降低定位算法的定位精度，该算法通过引入参考终端，利用载波相位的双差测量值来消除钟差的影响。考虑到锁相环不失锁整周模糊度不变的特性，设计了一种解算整周模糊度的迭代算法。此外，分析了周跳对本文所提算法的影响。仿真结果表明，该算法可以完全消除钟差的影响，并在短时间内精确解算整周模糊度，实现厘米级的三维定位。