非均匀风下流线型箱梁悬索桥静风稳定性分析

单秋伟，张亮亮,2，言志超，杨建新

(1. 重庆大学 土木工程学院，重庆 400045；2. 重庆城市科技学院，重庆 402167；3. 四川建筑职业技术学院，四川 德阳 618000；4. 湖南省澧县住房与城乡建设局，湖南 常德 415500)

随着桥梁建设能力的提升，桥梁跨径越来越大，但跨径的增大往往会使桥梁趋于轻柔，进而降低桥梁的稳定性。桥梁在建造和使用过程中一般需要考虑风灾、撞击和震害等影响，其中，风灾对桥梁结构的影响最为剧烈，发生频率也最高，由此造成的社会经济损失最为严重[1]。因此，在修建大跨度桥梁时，必须要考虑到桥梁结构对风作用的响应，并采取相应的措施降低其对结构的影响。

许多学者对大跨度桥梁的静风稳定性开展了研究。Boonyapinyo等[2]采用有限元方法，考虑桥梁几何非线性以及位移相关风荷载非线性，对大跨度斜拉桥在风荷载作用下的弯扭屈曲失稳临界风速进行了计算。程进等[3]采用非线性方法开展了江阴长江大桥的参数分析和比较，发现悬索桥的静风稳定性随着初始攻角的增大而降低。Cheng等[4-6]提出了大跨度斜拉桥和悬索桥静风稳定性的非线性方法，并开发了相应的分析程序。Boonyapinyo等[7]提出了一种考虑位移非线性、几何非线性和材料非线性的大跨度悬索桥静风稳定性的非线性分析方法，并分析了影响大跨度悬索桥静风稳定性的因素。李永乐等[8]采用风荷载增量和双重迭代相结合的方法对大跨度悬索桥的静风失稳形态以及机理进行了研究。Xu等[9]研究了斜拉桥的非线性静风稳定性，发现初始风攻角对桥梁静风稳定性影响极大。管青海等[10-11]分析了大跨度悬索桥的静风失稳发展过程以及影响因素。张文明等[12-13]研究了平均风速空间分布下悬索桥的静风稳定性，结果表明，风速空间分布对悬索桥静风稳定性的影响不可忽略。Zhou等[14]研究了双主跨悬索桥的静风失稳模式和破坏机理，发现此类悬索桥存在两种失稳模式。张玉琢等[15]在进行静风稳定性分析时发现非线性效应对静风稳定性的影响不可忽视。Dong等[16]基于逆可靠度评估法分析了大跨度斜拉桥的静风稳定性安全系数。胡朋等[17-18]对山区峡谷非均匀风场下大跨度斜拉桥的静风稳定性进行了分析，结果表明，非均匀风攻角下大桥的静风失稳临界风速远远低于均匀风攻角下的静风失稳临界风速。

上述研究多集中在空间均匀风下的静风稳定性，对非均匀风下的静风稳定性研究较少，因此，有必要对大跨度悬索桥在非均匀风下的静风稳定性开展研究，从而保证大跨度悬索桥在建设和运营状态下的安全。笔者利用有限元分析软件ANSYS的APDL语言，采用非线性分析方法，对非均匀风攻角和非均匀风速下大跨度悬索桥的静风稳定性进行分析。

1 静风稳定性分析理论

1.1 风的静力作用

平均风作用会使处在风场中的结构产生一定的变形，风的作用相当于一个静荷载[1]。将此荷载沿桥梁主梁断面分解为阻力、升力和升力矩，称为风荷载的三分力，如图1所示。

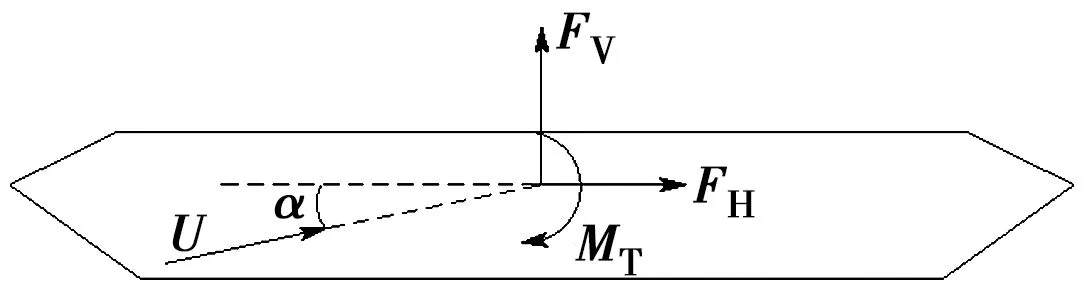
图1 风荷载的三分力

对于外形相似的截面，其受到的静力风荷载与它们的特征尺寸成比例，因此，可以引入无量纲的静力三分力系数来描述静力风荷载的共同特征。借助三分力系数，可将静力风荷载表示为[1]

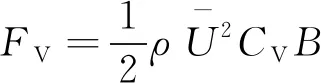
(1)

(2)

(3)

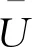
静力三分力系数随主梁断面形式、主梁高宽比以及雷诺数等的变化而变化，三分力系数也是风攻角α的函数。研究三分力系数的方法主要有节段模型风洞试验和计算流体力学(CFD)，相较而言，风洞试验技术更为成熟，所得结果更加可靠。

采用节段模型风洞试验，对某悬索桥主梁在12°～ +12°风攻角范围内的三分力系数进行测定，结果如图2所示。

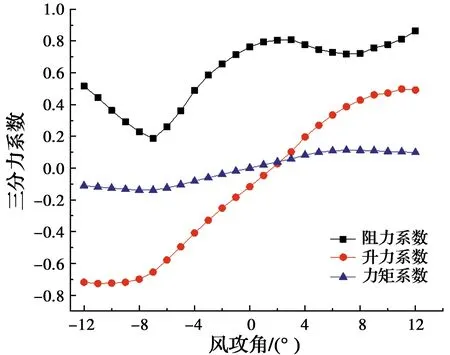
图2 主梁在体轴下的三分力系数

1.2 静风稳定性非线性分析方法

大跨度悬索桥在静力风荷载下存在明显的非线性问题，在进行非线性分析时主要考虑大跨度悬索桥的材料非线性、几何非线性以及静风荷载非线性[19]。

张志田等[20]论述了材料非线性对静风稳定性的影响，发现结构材料在整个失稳过程中始终处于线弹性状态，表明对大跨度悬索桥进行非线性静风稳定性分析时一般可以忽略材料非线性的影响。程进等[3]研究了主缆垂度对大跨度悬索桥静风稳定性的影响，发现桥梁静风稳定性与主缆的垂度效应关系不大。因此，笔者在进行非线性分析时，仅考虑结构大位移和大变形效应的影响。

荷载非线性是指悬索桥主梁受到的静力风荷载与主梁变形存在着非线性关系。对于大跨度悬索桥，静风稳定性的非线性分析可以归结为求解式(4)的非线性平衡方程[21]。

(4)

式中：Ke为结构的线弹性刚度矩阵;Kg为结构的几何刚度矩阵;u为节点位移向量;P(α)为静力风荷载作用下结构的荷载向量，α为有效风攻角。

对于非线性平衡方程式式(4)，左侧的结构刚度与结构变形存在非线性关系，右侧的荷载向量也是结构变形的函数，因此，对该方程进行求解时需要采用迭代法。将该方程写成增量方程组的形式

{Pj(αj)-Pj-1(αj-1)}

(5)

式中各参数的物理意义同式(4)。

借助ANSYS对大跨度悬索桥进行非线性静风稳定性分析的具体过程:

1)给出初始风攻角α0和初始风速U0以及风速步长ΔU；

2)根据此时的风攻角和风速，计算主梁受到风荷载的三分力；

3)在ANSYS的静态分析中，采用完全Newton-Rapson法求解式(5)，得出模型主梁的位移，并从中提取出主梁各单元的扭转角，重新计算主梁受到风荷载的三分力；

4)计算三分力系数的欧几里得范数，当范数大于给定值时，重复执行过程3)，使主梁达到该风速下的平衡状态，若范数小于给定值，则增加一级风速，重复执行过程2)和3)；

5)若在计算过程中，出现了迭代不收敛，则将风速调整到上一次迭代状态，减小风速步长，再进行计算，相邻两次迭代风速差值满足要求时便可终止计算，相对应的最后一级风速即是失稳临界风速。

2 大跨度悬索桥有限元模型

某大跨度悬索桥，全长为1 600 m，由主桥和引桥构成，主桥跨径为880 m。南引桥共两联，总长分别为230、240 m，其中，第1联为连续梁结构，第2联为连续刚构结构；北引桥长度为240 m，采用连续刚构结构。中跨主缆的矢跨比为1/8.8，桥梁的立面整体布置如图3所示。

图3 某大跨度悬索桥立面布置图(单位：m)

大桥主梁采用闭口薄壁扁平钢箱梁，箱梁总宽为42.0 m，吊索间距为39.2 m，高度为3.5 m。主梁横断面如图4所示。

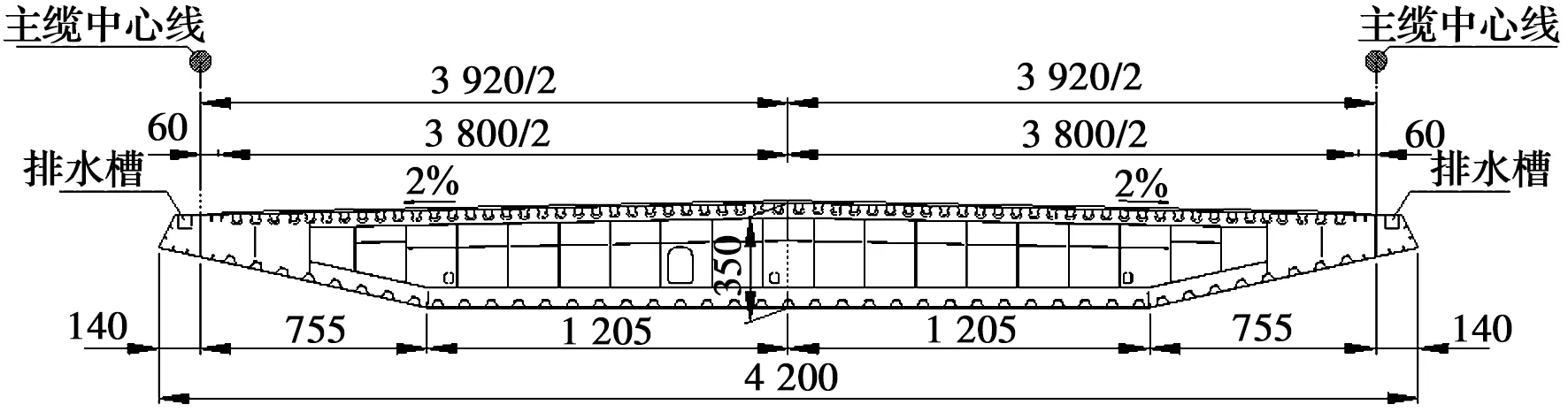
图4 某大跨度悬索桥主梁断面示意图(单位：cm)

在ANSYS中，采用单主梁模型模拟主梁，单元类型选用beam4；主塔因其为变截面，故采用3D渐变梁单元beam44模拟；采用link10杆单元模拟主缆和吊索；mass21质量单元模拟主梁的质量惯矩和二期恒载。

大桥的边界条件设置为：主塔底部固结，主缆锚固处固结，桥塔下横梁与主梁采用耦合自由度方式进行连接，主塔下横梁处设置combin14弹簧单元模拟纵向阻尼器，以限制主梁纵向位移。

全桥有限元模型共计705个节点，887个单元，如图5所示。

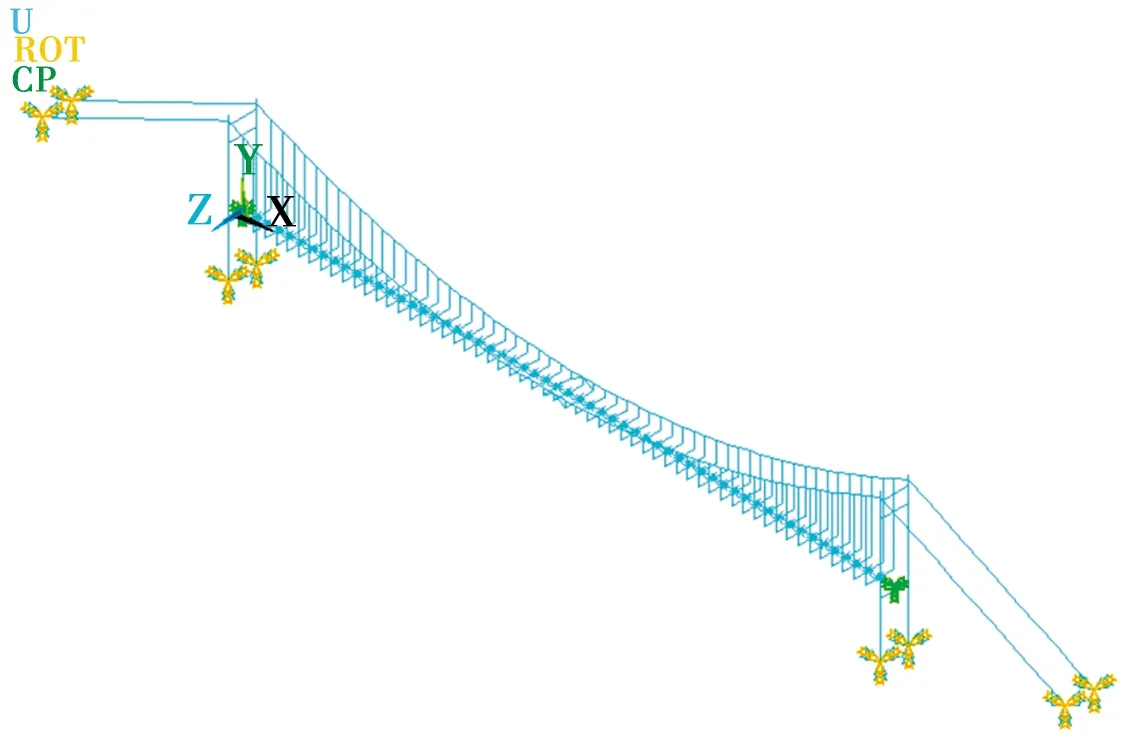
图5 大桥的有限元模型

3 非均匀风攻角下的静风稳定性

自然界中的风场都是非均匀的，而前人的研究多以均匀流场为基础，这样的研究结果与真实情况可能存在偏差，因此，有必要开展非均匀风场下悬索桥的静风稳定性分析。

为了研究非均匀风场中的非均匀风攻角风场对流线型箱梁悬索桥静风稳定性的影响，根据风攻角分布区间的不同，设置了如图6所示的两类风攻角分布工况。

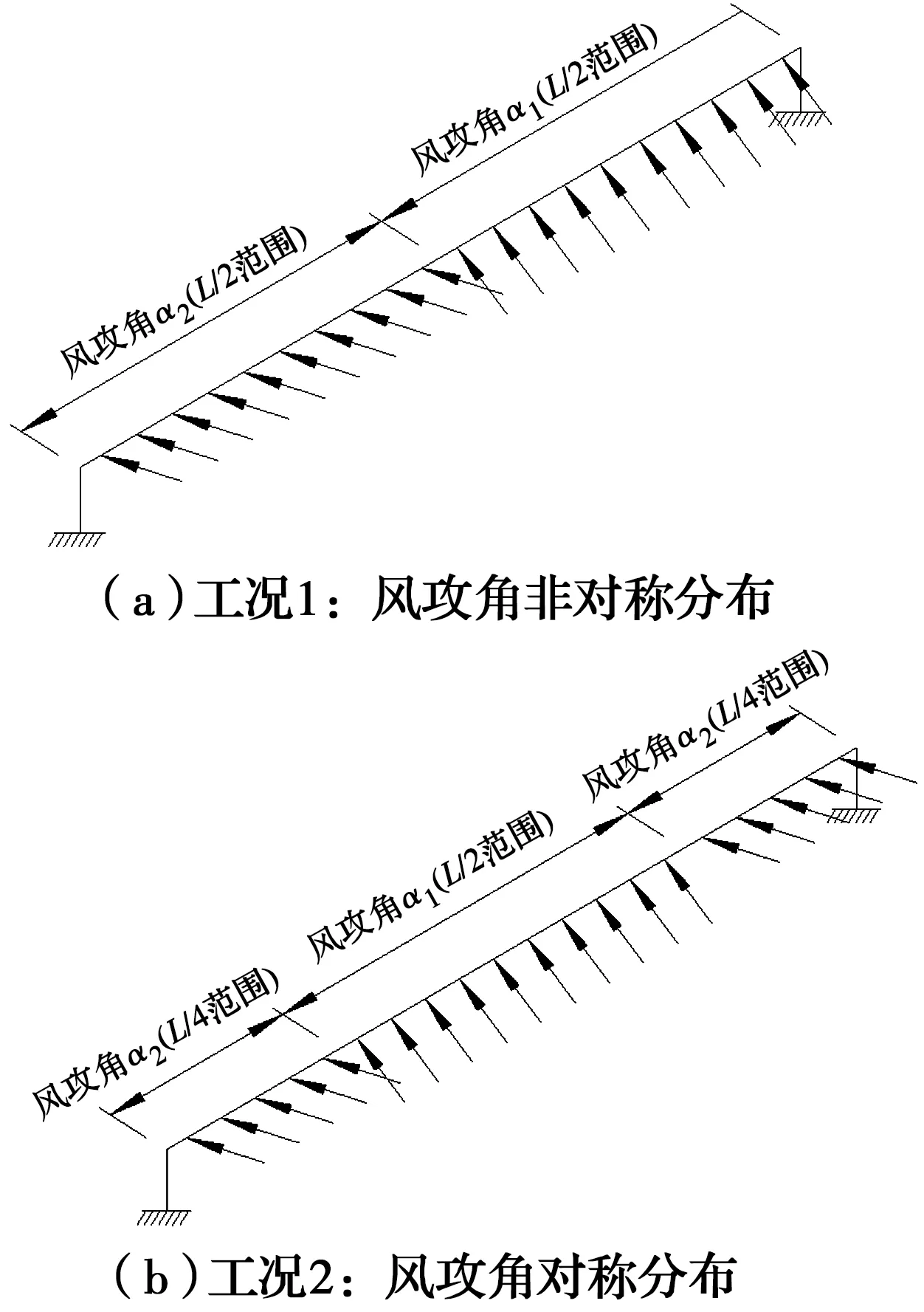
图6 非均匀风攻角来流工况设置示意图

工况1考虑风攻角沿着桥跨方向非对称分布的情况，主梁右半跨来流风攻角为α1，左半跨来流风攻角为α2。工况2则考虑风攻角沿着桥跨方向对称分布的情况，主梁跨中1/2跨度范围来流风攻角为α1，主梁两端各1/4跨度范围来流风攻角为α2。

为了深入分析非均匀风攻角大小关系对静风稳定性的影响，对于工况1和工况2，设置了如表1所示的3种风攻角大小关系。风攻角正负号规定：来流对主梁产生向上的作用力时为正攻角，反之则为负攻角。图7为风攻角关系情况Ⅲ的来流作用示意图，其他攻角关系情况可以由此类推。

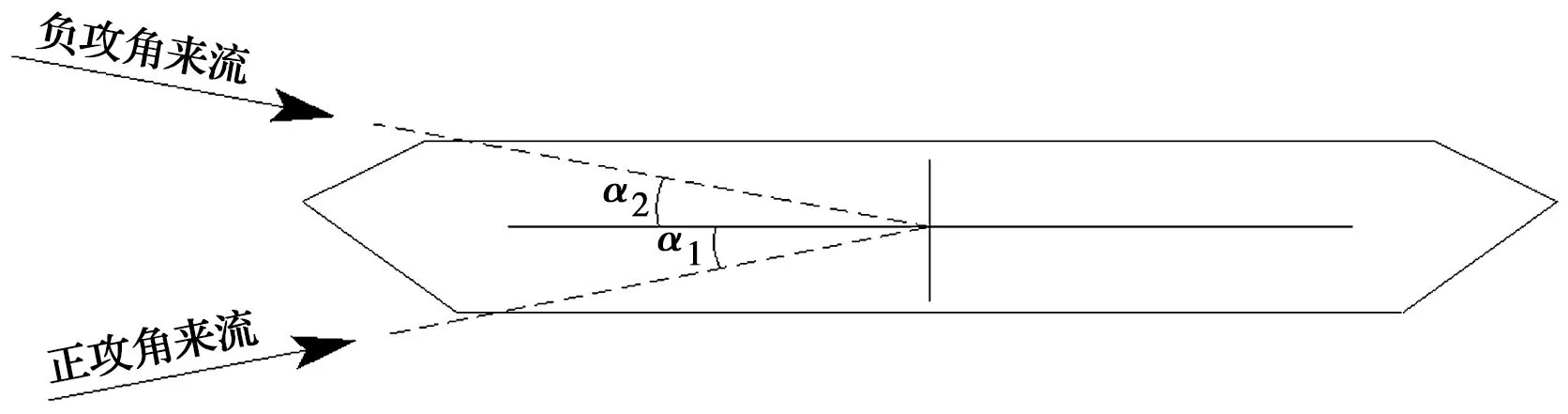
图7 攻角关系情况Ⅲ来流作用示意图

表1 风攻角大小关系设置

3.1 非均匀风攻角下静风失稳临界风速

对于0攻角与正攻角(情况Ⅰ)来流情况，借助ANSYS算得悬索桥在静风荷载下的失稳临界风速Ucr如图8所示。

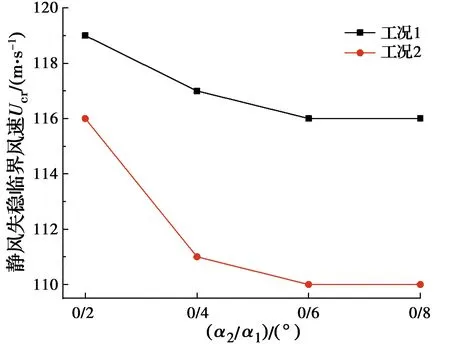
图8 风攻角分布情况Ⅰ的静力失稳临界风速

由图8可知，对于工况1和工况2而言，随着正攻角α1的增大，静力风荷载下的失稳临界风速Ucr均逐渐降低，说明正攻角对桥梁的静风稳定性存在不利影响，会降低桥梁的静风稳定性。但正攻角α1对静风失稳临界风速影响并不是线性的，当正攻角增大到一定程度时，结构的失稳临界风速减小的程度不明显。

同时，对比工况1和工况2可以发现，当主梁跨中附近作用了正攻角来流时，结构的静风失稳临界风速有着进一步的降低，说明与非对称分布工况相比，来流对称分布对桥梁的静风稳定性有着更不利的影响。

对于0攻角与负攻角(情况Ⅱ)来流情况，算得的静风失稳临界风速Ucr如图9所示。

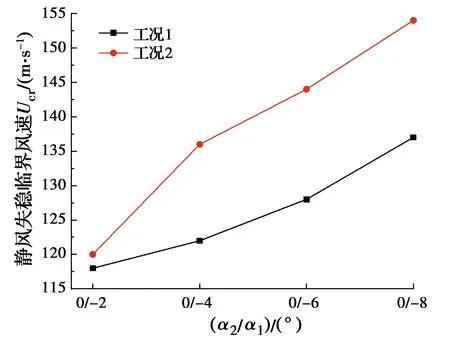
图9 风攻角分布情况Ⅱ的静力失稳临界风速

由图9可以得出，工况1与工况2在静风荷载下的失稳临界风速Ucr随着负攻角α1的减小而增大，这表明负攻角来流有利于桥梁抵抗静风失稳。对比风攻角沿桥跨的两种分布模式，工况2的失稳临界风速要高于工况1的失稳临界风速，说明负攻角来流情况下，风攻角沿桥跨非对称分布对桥梁静风稳定性的影响更为不利。

为了对比风攻角α1的正负对桥梁静风稳定性的影响程度，定义桥梁在最初风攻角状态下的静风失稳临界风速为Ucr，0，并定义偏差幅度v以表征影响程度的大小，其计算公式为

(6)

由式(6)算得情况Ⅰ、Ⅱ下静风失稳临界风速的偏差幅度v见图10。由图10可知，α1为负值时桥梁静风失稳临界风速的偏差幅度v明显大于α1为正值时的偏差幅度，表明正风攻角来流对桥梁静风失稳临界风速的降低程度小于负风攻角来流对桥梁静风失稳临界风速的提高程度。

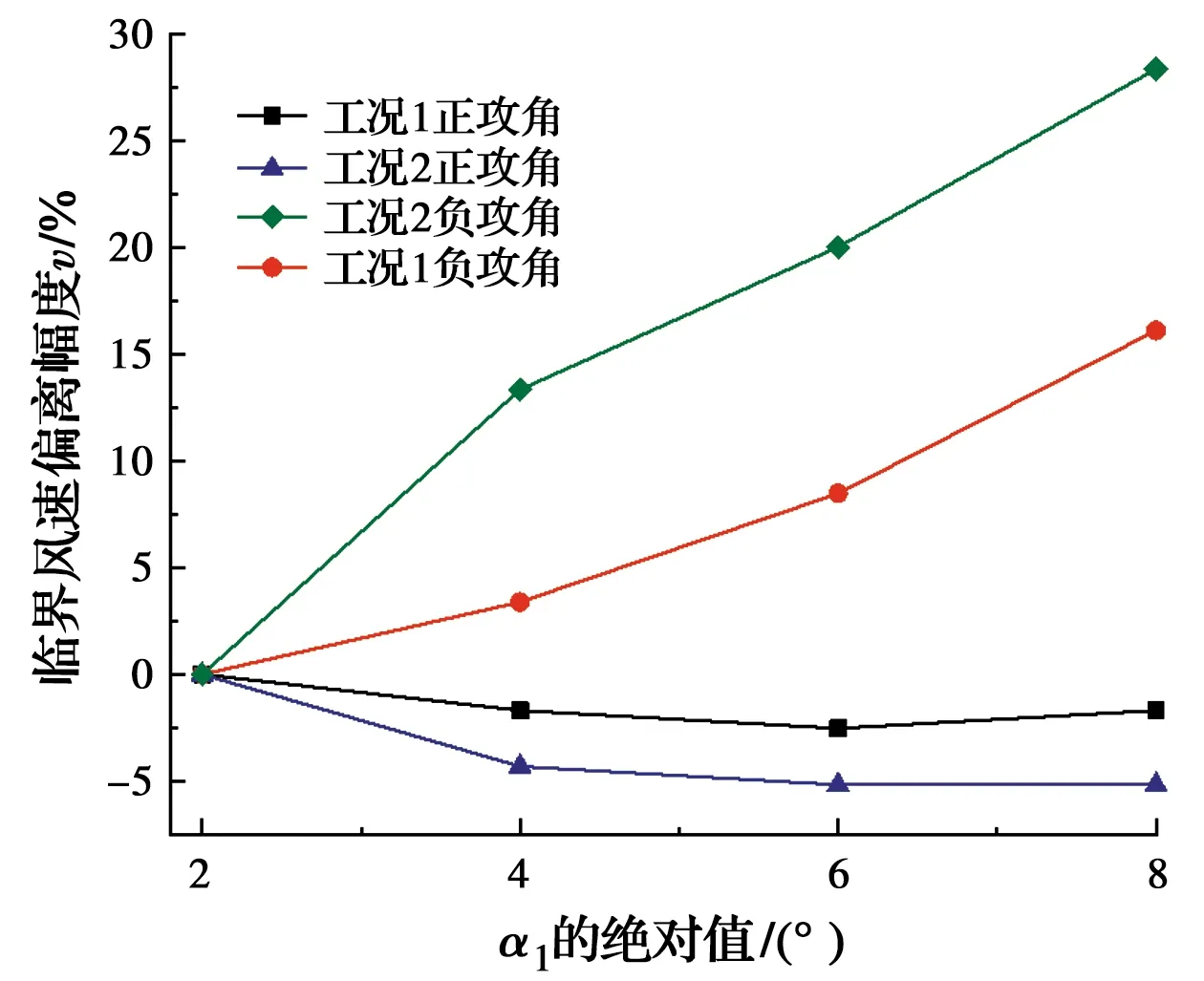
图10 临界风速偏离幅度v与α1的变化关系

正攻角与负攻角来流(情况Ⅲ)组合作用时，算得的悬索桥静风失稳临界风速Ucr如图11所示。

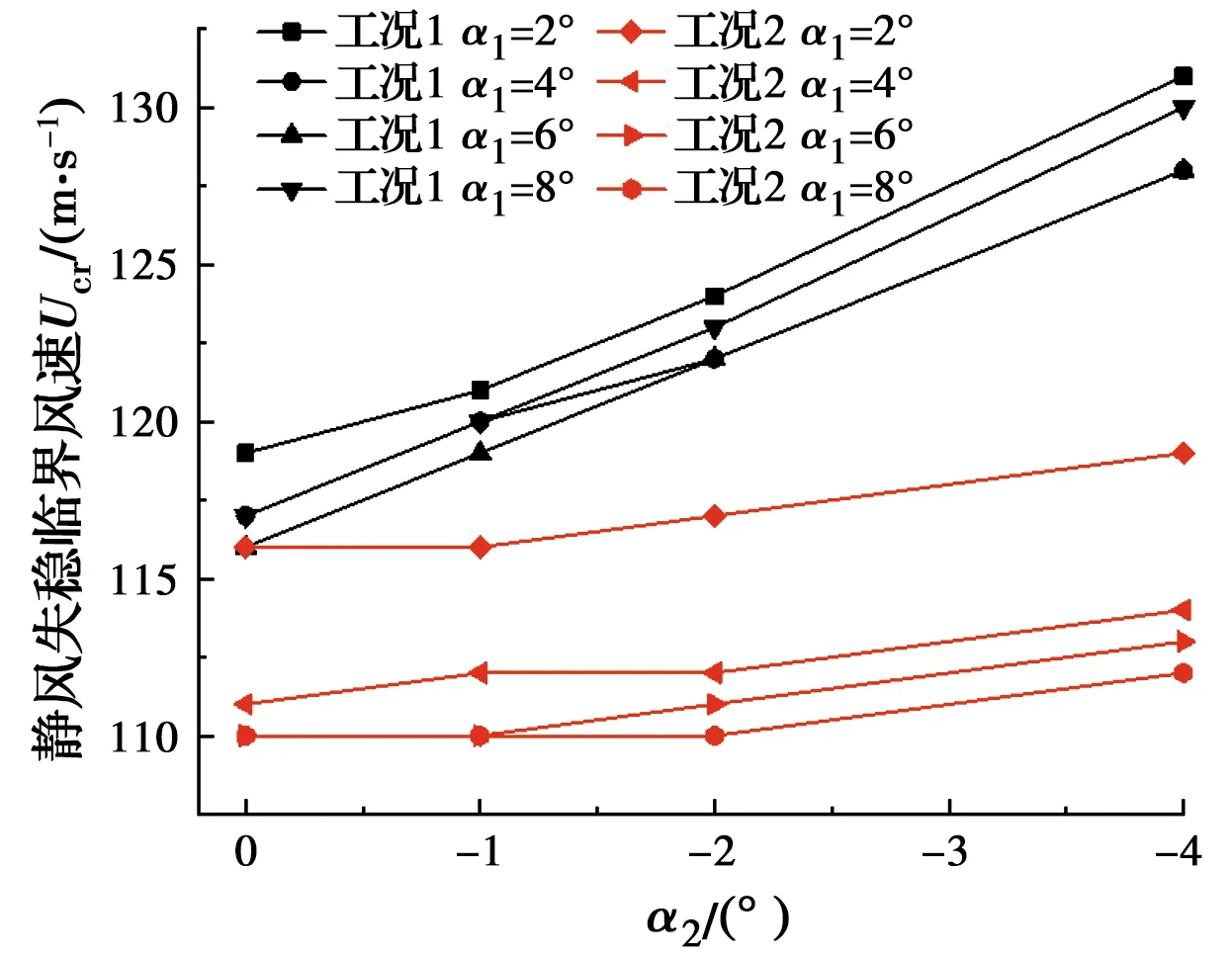
图11 风攻角分布情况Ⅲ的静力失稳临界风速

分析图11可以发现，在相同的来流条件下，工况1的静风失稳临界风速始终要高于工况2，说明在正负攻角来流组合作用时，风攻角沿主梁非对称分布对桥梁的静风稳定性相对于其沿主梁对称分布更有利。

对于工况2而言，当α1为一定值时，结构的静风失稳临界风速随α2的减小变化程度不大，而当α2为一定值时，静风失稳临界风速随着α1的减小有一定程度的提高。这表明主梁两端风攻角α2对桥梁静风稳定性影响不大，而跨中附近风攻角α1对桥梁静风稳定性有较大影响。说明对于风攻角对称分布工况，在正负攻角组合来流作用时，结构的静风稳定性主要由跨中附近作用的攻角为α1的来流决定，而作用在主梁两端攻角为α2的来流对静风稳定性的影响不明显。

3.2 非均匀风攻角影响的衡量方式

非均匀风攻角来流对结构静风稳定性的影响往往不能简单分析，为了适当衡量非均匀风攻角来流对结构静风稳定性的影响程度，提出了4类衡量方式。

方式Ⅰ：按照大风攻角沿桥梁跨度方向均匀分布时算得的桥梁静风失稳临界风速Umin来衡量桥梁的静风稳定性。定义此风速与桥梁实际静风失稳临界风速Ucr的偏离幅度为a，计算公式为

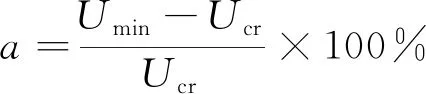
(7)

方式Ⅱ：按照小风攻角沿桥梁跨度方向均匀分布时计算出的桥梁静风失稳临界风速Umax来衡量桥梁的静风稳定性。定义此方式的偏离幅度为b，计算公式为

(8)

方式Ⅲ：定义非均匀风攻角下桥梁的静风失稳临界风速为Umean，其计算公式为Umean=(Umin+Umax)/2，以此风速来衡量桥梁的静风稳定性。定义此方式的偏离幅度为c，计算公式为

(9)

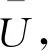
(10)

工况1、工况2下，上述4种衡量方式的偏离幅度计算结果如图12所示。

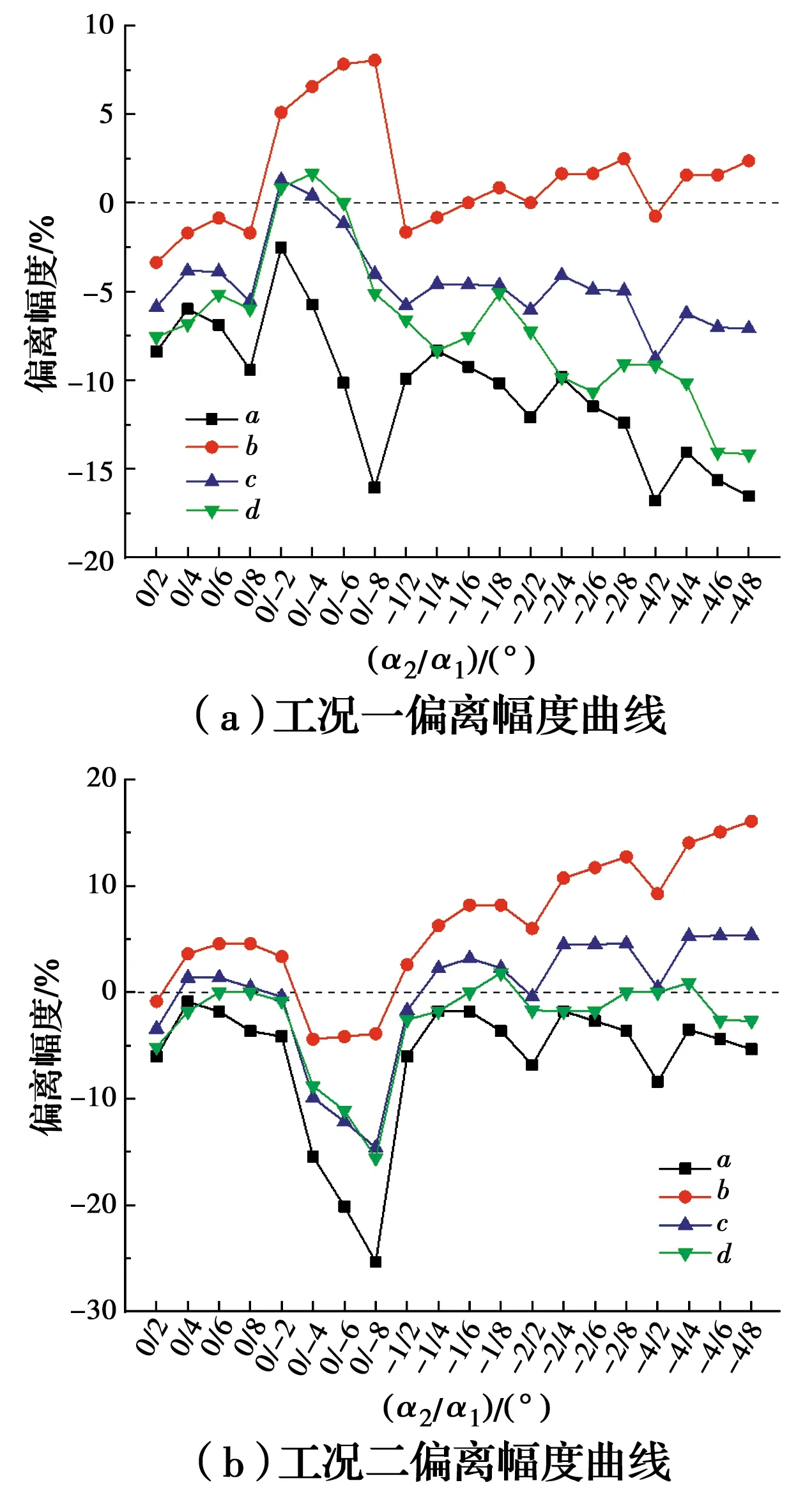
图12 四种衡量方式的偏离幅度

由图12(a)可知，上述4种衡量方式所对应的偏离幅度a、b、c、d中，衡量方式Ⅱ的偏离幅度b最接近0，方式Ⅰ的偏离程度a最大，说明此衡量方式偏离实际情况的程度最严重，方式Ⅲ的偏离幅度c和方式Ⅳ的偏离幅度d也较大。说明对非对称风攻角工况采用较小风攻角计算的静风失稳临界风速最接近实际情况，因此，可以采用小风攻角对非均匀风攻角来流进行静风稳定性分析。但需要注意的是，当半跨来流风攻角接近于0°，另半跨来流负风攻角较大时，方式Ⅱ的偏离幅度较大，说明偏离程度较远，此时，需要按照方式Ⅲ或方式Ⅳ来衡量静风稳定性。

由图12(b)可知，工况2下衡量方式Ⅳ的偏离幅度d在整体范围内最接近0，表明对于风攻角对称分布工况，可以采用大小风攻角的平均值进行非均匀风攻角来流下桥梁静风稳定性的分析。但当主梁端部攻角接近于0°，跨中附近负攻角较大时，方式Ⅳ的偏离幅度较大，此时，应该采用小风攻角进行静风稳定性分析。

4 非均匀风速下静风稳定性

作用在大跨度悬索桥上的风，除了风攻角的分布存在不均匀的情况外，风速大小也可能沿着桥跨方向出现不均匀的情况。当风速分布不均匀时，为了便于分析，设置了两类风速非均匀分布工况，如图13所示。

参考明渠流流层流速分布规律，采用指数规律来描述主梁上的风速变化。工况1考虑风速沿主梁非对称分布情况：主梁一端风速为U1，另一端风速为U2，主梁上的风速由U1到U2呈指数律变化。工况2考虑风速沿主梁对称分布情况：主梁端部风速为U1，跨中风速为U2，端部到跨中的风速由U1到U2呈指数律变化。

为了分析风速的非均匀程度对大跨度悬索桥静风稳定性的影响，设置了如表2所示的风速比值关系。

表2 风速比值设置

4.1 非均匀风速下静风失稳临界风速

非均匀分布风速下大桥静风稳定性的比较须在同一基准下进行。以主梁全长范围内非均匀分布风速下单位时间内总流量与均匀分布风速下单位时间内总流量相等为原则，在主梁全长范围内对风速积分后取平均值作为平均静风失稳临界风速Ucr,即式中：L为主梁全长；u(l)为非均匀风速下主梁上各点的风速值。

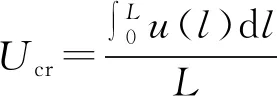
(11)

在计算过程中，根据大桥所在桥址处的风环境，考虑来流的风攻角为+2°。非均匀风速下大桥的平均静风失稳临界风速计算结果如图14所示。

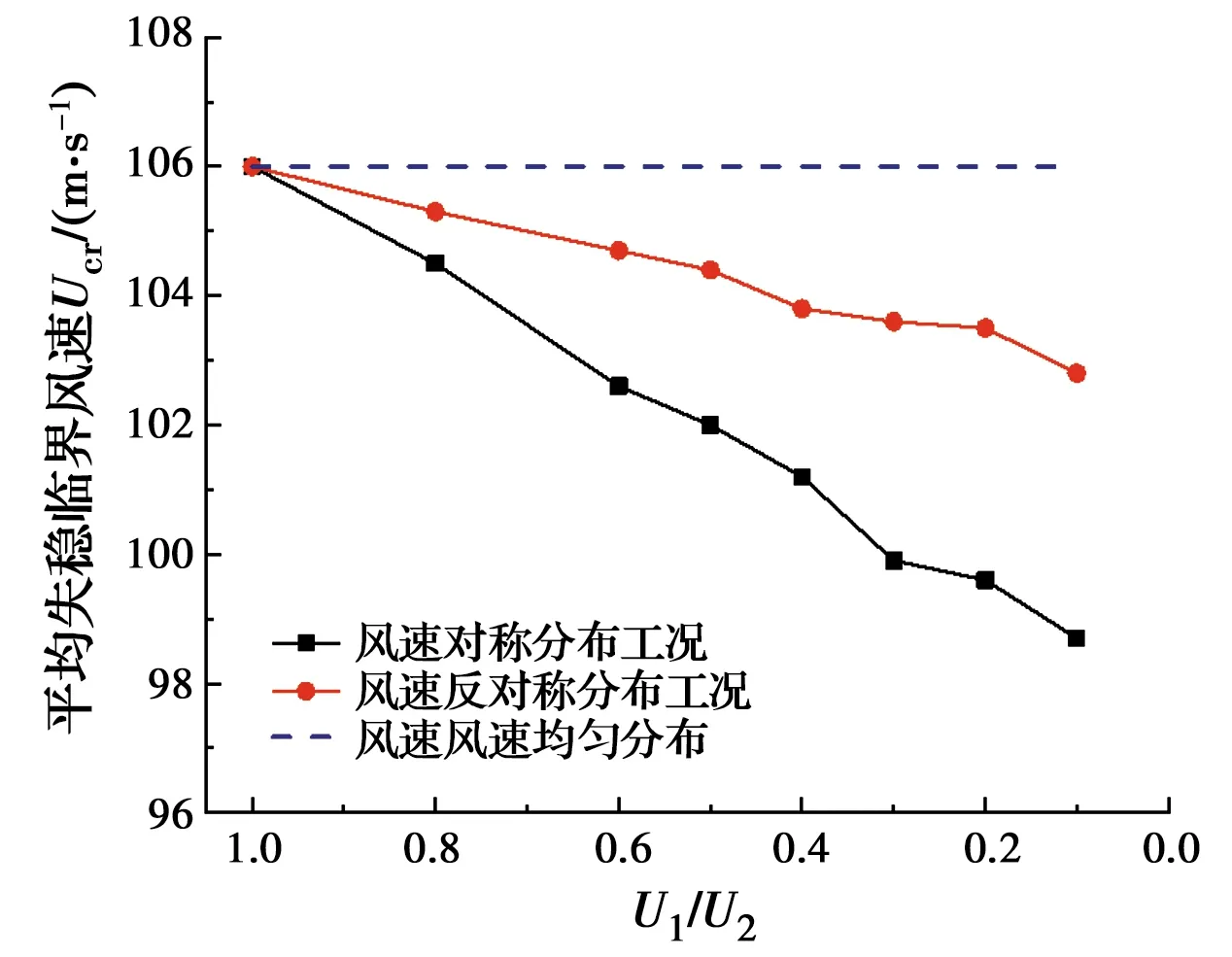
图14 平均静风失稳临界风速与风速比值的关系

由图14可以发现，在两类风速分布工况下，大桥的平均静风失稳临界风速随着风速比值U1/U2的降低而降低，表明风速非均匀分布不利于流线型箱梁悬索桥抵抗静风失稳，会降低其静风稳定性。此外，风速对称分布工况下，大桥的平均静风失稳临界风速降低幅度比非对称分布工况下的降低幅度大，说明风速对称分布工况更加不利于该类型悬索桥抵抗静风失稳。

4.2 不同风攻角下非均匀风速来流对静风稳定性的影响

上述分析仅考虑了给定攻角下的非均匀风速，为了说明不同初始风攻角下非均匀风速对静风稳定性的影响，以工况2为例，分析了-2°、0°、+2°、+4°、+8°攻角下的非均匀风速来流对桥梁静风稳定性的影响。其中较小的攻角主要是考虑大桥所在桥址以及周围环境，较大的攻角则是考虑一些极端气候因素以及局地强风影响。不同风攻角下不同风速比值的平均静风失稳临界风速如图15所示。

由图15可知，不同初始攻角下，非均匀风速来流对桥梁静风稳定性有着相似的影响，在-2°、0°、+2°、+4°、+8°攻角下，悬索桥的平均静风失稳临界风速均随着风速比值减小而降低，这与前述分析相吻合，也表明了风速非均匀分布不利于流线型箱梁悬索桥抵抗静风失稳。

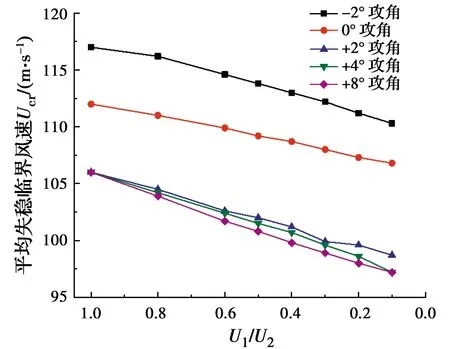
图15 不同攻角下非均匀风速的平均临界失稳风速

5 结论

以某一流线型箱梁悬索桥为背景，采用有限元方法分析了悬索桥在非均匀风作用下的非线性静风稳定性，得到以下结论：

1)当非均匀风攻角来流作用时，随着正攻角的增大，桥梁的静风失稳临界风速逐渐降低，正攻角会降低桥梁的静风稳定性。随着负攻角的增大，桥梁的静风失稳临界风速逐步提高，负攻角有利于桥梁的静风稳定性。通过对比正负攻角的影响程度，发现负攻角对桥梁静风稳定性的影响程度比正攻角的影响程度大。

2)当非均匀风攻角来流非对称分布时，由小风攻角确定的桥梁静风失稳临界风速可以在一定程度上代表桥梁实际来流情况下的静风失稳临界风速；当非均匀风攻角来流对称分布时，可以选择平均攻角确定的静风失稳临界风速来衡量桥梁的静风稳定性。

3)非均匀风速来流会降低桥梁的静风失稳临界风速，对桥梁的静风稳定性有不利影响，并且来流风速对称分布时对该类型桥梁静风稳定性的影响比来流风速非对称分布时的影响更大。不同初始攻角下，非均匀风速来流对桥梁静风稳定性有着相似的影响，悬索桥的平均静风失稳临界风速均随着风速非均匀程度增大而降低。