基于多列卷积神经网络的参数异步更新算法

陈薪羽，刘明哲*，任 俊，汤 影

（1.地质灾害防治与地质环境保护国家重点实验室（成都理工大学），成都 610059；2.四川轻化工大学人工智能学院（自动化与信息工程学院），四川自贡 644000；3.成都理工大学计算机与网络安全学院（牛津布鲁克斯学院），成都 610059）

0 引言

人群计数技术旨在自动估计图像中出现的人数［1］。随着城市的发展和人口的增加，人群活动逐渐增多。近年来，为了实现人流控制和保障公共安全，从静态图像或视频中更加准确地估计或预测人群数量已经变得越来越重要，相关部门为了加强公共安全，也实施了相应政策，表示将开展视频监控的全面联网，提升公共安全保障能力［2］。人群计数算法也有可能应用于其他领域，如物体计数、细胞计数、高分辨率图像细菌计数或交通堵塞预测等。

人群计数研究中会受到实际环境、光照、气候、拍摄角度、背景干扰等的影响。现有的人群计数算法通常采用从每个像素中提取图像特征的思想，通过神经网络模型的训练来学习像素特征与密度分布图之间的映射关系，最后用训练好的神经网络模型生成目标密度图［3］。基于深度学习的密度估计算法主要分为基本网络模型、规模自适应模型、上下文感知模型和多任务学习网络模型。

为了提取图像尺度不变特征，研究了多列卷积组成的卷积神经网络模型。Zhang 等［4］提出了一种多列卷积神经网络结构（Multi-column Convolutional Neural Network，MCNN），它能应用在具有任意人群密度和透视变化的图像上，该算法通过构造多列的网络对图像不同尺度特征进行提取，适应较大的尺度变化。另外，他们从高密度图中发现，人头部大小与相邻两个人的中心之间的距离有关，并拓宽训练数据，建立了一个新的上海科技数据集（ShanghaiTech Dataset）。此外Cheng 等［5］提出了一个多列多任务学习（Multi-column Multitask Learning，McML）算法，采用两列结构和多任务学习方式学到更多网络参数信息。Boominathan 等［6］提出了一个双列卷积神经网络模型，通过融合底层特征来估计人数。

Ranjan 等［7］使用了一种新的训练算法，通过增加不同分辨率的图像来提升模型整体性能；文献［8-9］中设计了尺度不变的卷积层或者池化层，提及的BSA-CNN（Body Structure Aware Convolutional Neural Network）具有相同大小卷积核，使得提取的特征具有尺度不变性；Sam 等［10］深入研究了尺度自适应网络用于更精准地估计人群数目。虽然这些算法都在一定程度上改善了图像尺度变换大的问题，但忽略了从原始图像中学习特征的每一列卷积神经网络之间的关系，导致网络参数大量冗余甚至模型过拟合，影响检测计数准确性及效率。

为此，本文提出了一种基于多列卷积神经网络的参数异步更新算法A-MCNN（Asynchronous MCNN）。该算法与MCNN 相比，最大不同在于每两列间加入了交互信息（Mutual information）列学习每列特征图的关联性，并且每列的权重参数采用交替更新的方式，通过交替更新各列卷积神经网络参数，减轻网络学习压力，同时用交互信息学习各列卷积神经网络之间的内在关系，使得每一列都可以从输入图像中提取更多的判别特征，减少整个模型的冗余参数，防止过度拟合，更加适应检测图像目标大尺度变换。

1 人群计数法

1.1 相关原理

人群计数的最新研究将人群计数问题视为密度回归任务［11］。具体而言，若数据集包括R幅图像，则这R幅图像可以表示为X=[x1，x2，…，xR]，每幅图像xi都标注了Ci个行人头部中心点，表示为。具体地，图像xi的真实密度图yi为：

其中：p为图像xi中的像素，对应图中人头部中心点P1，P2，…，；像素的密度表示为高斯核函数Ngt；σ为标准偏差；μ为方差。输入图像xi的总人数Ci等于图像xi中所有像素的密度之和，表示为：

利用训练数据集，人群计数模型旨在学习具有参数α的回归模型G，以最小化估计密度图Gα(xi)和真实密度图yi之间的差异。欧几里得距离是一种广泛使用的损失函数，用于衡量训练模型的质量，并获得近似解，L2损失函数表示为：

由于输入图像的分辨率变化，式（3）损失函数方程通常应根据输入图像的分辨率大小进行归一化处理。

1.2 本文算法

如图1 所示，A-MCNN 由三列卷积异步更新结构、列之间的交互信息、动态卡尔曼滤波（dynamic Kalman filter）组成。首先输入单帧视频图像，经过三列卷积结构分别提取不同尺度特征，通过列之间的交互信息使得各列更多学习不同尺度特征，并根据交互信息依次单独循环更新每列参数；整个模型收敛后，采用动态卡尔曼滤波将各列采用1×1 卷积层输出的预测密度图进行图像深度融合，得到最终的密度估计图；利用式（2）对密度图中所有像素求和，得到估计的图像总人数。

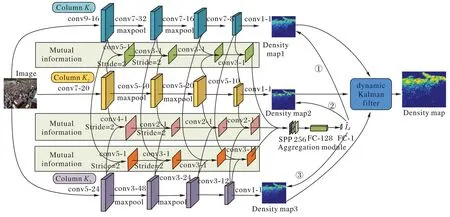
图1 A-MCNN算法整体结构Fig.1 Overall structure of A-MCNN algorithm

整个模型集成了多列之间的聚合模块（Aggregation module）结构，由空间金字塔池化SPP 256（Spatial Pyramid Pooling 256）、全连接层FC-128（Full Connection Layer-128）和FC-1 组成，以自动评估列之间的相互信息。聚合模块的结构本质上是一个分类器，可以对列之间的相同信息和不同信息进行分类。列之间的所有特征都被输入到分类器中，分类器输出列之间的交互信息。使用交互信息的目的是显示不同列之间的尺度相关性。也就是说，交互信息越少意味着列之间的特征关联越少。因此，通过减少列之间的交互信息，A-MCNN 算法可以引导每列更多地关注图像中包含的不同尺度信息。与以前的多列算法不同，A-MCNN 算法交替更新和优化每列的参数，直到整个网络聚合。在学习每一列的特征时，首先将列之间的交互信息作为指导参数更新的先验条件；接下来，借助于列之间提供的相互信息，整个模型可以交替地引导每列学习不同的尺度特征和不同分辨率的图像。

具体来说，A-MCNN 算法中，有三列卷积结构用于异步更新参数。从交互信息中学习图像共同的特征和差异后，交互信息将返回到每列，使得每列能够学习更多不同的图像信息，在这种情况下，它将减少冗余参数并避免过度拟合。如图2 所示，网络参数异步更新时各列的更新顺序不同，第一列的更新是基于都与第一列有关的不同的交互信息，然后交互信息通过聚合模块分类后返回到第一列，使得第一列可以学习自身与其他列的区别，并根据损失函数和交互信息更新该列。第一列更新时，其他列都保持不更新状态，在第一列完成更新后，第二列开始参数更新；由于第一列进行了参数更新，所以第一列和第二列之间的交互信息发生改变；由于第二列和第三列还没有进行参数更新，所以第二列和第三列之间的交互信息暂时保持不变。然后第二列在学习自己和其他列的相互信息后更新参数。同样地，在第二列更新参数时，其他列保持不更新状态。在第二列更新完成后，第三列开始遵循相同的模式更新，此时的第一列和第二列都已经更新过，所以第三列与第一列以及与第二列之间的交互信息都发生了改变，根据更新的交互信息进行该列网络参数更新，直到三列网络参数都实现最优化时，结束网络参数异步更新流程，输出每列CNN 预估密度图，再根据动态卡尔曼滤波实现图像融合，得到最终估计密度图。

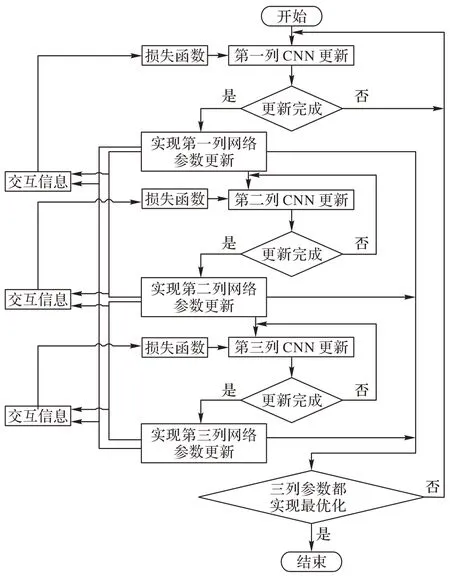
图2 网络参数异步更新流程Fig.2 Asynchronous updating process of network parameters

在整个模型训练中，参数分别为K1、K2和K3的三列交替训练，其中每列由三个损失函数联合训练，分别表示为：

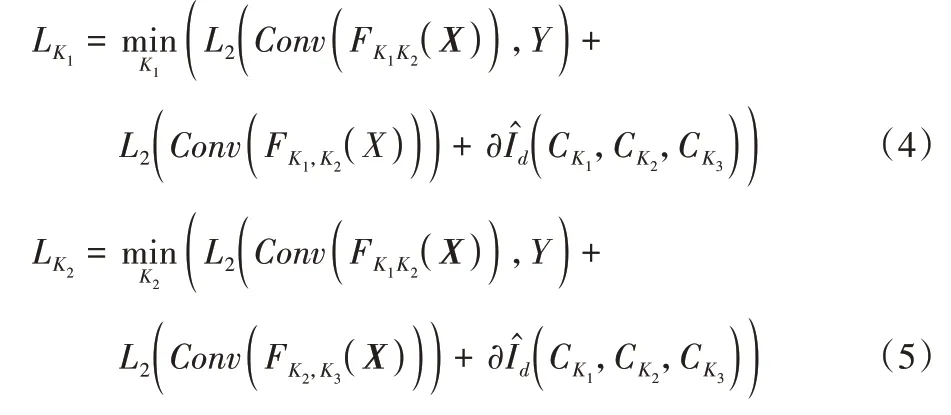
其中：L2损失函数用于减少人群计数的误差值；交互信息的值由聚合模块Gd计算，参数用于缩小列之间的交互信息；∂是平衡三个损失函数的权重参数；是来自三列的不同卷积层的卷积特征，用于交互信息评估；表示K1和K2两列的最后一个卷积层上的特征要素串联；表示K2和K3两列的最后一个卷积层上的特征要素串联。

1.3 交互信息

交互信息是变量之间相关性的基本度量。在A-MCNN算法中，三列结构被用作不同的变量特征，因此，交互信息可以反映不同列之间特征的相关程度，如图1 中，ColumnK1、ColumnK2、ColumnK3为三列卷积的主体结构，每两列主体结构之间的“Mutual information”列则为交互信息列，用于学习每两列主体结构特征图提取特征的关联性。基于前人工作的成功和可行性［12］，使用交互信息来表示不同列的冗余参数的程度，目的是为了使每一列学习更多不同尺度的信息，使用计算交互信息的方式来降低每一列的相关性，使得每一列学习图像的不同特征和分辨率。具体来说，本文将特征之间的交互信息分为之间、之间、之间的交互信息。以之间的交互信息为例，特征和之间的交互信息表示为：

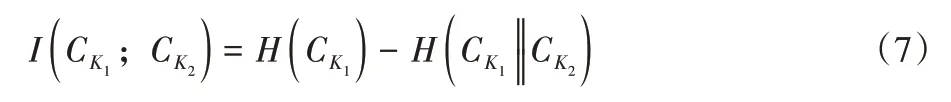
其中：H是香农熵（the Shannon entropy）；表示给定的不确定性。根据前人工作有效性证明［13］，使用库尔巴克-莱布勒（Kullback-Leibler）散度计算交互信息，表示为：

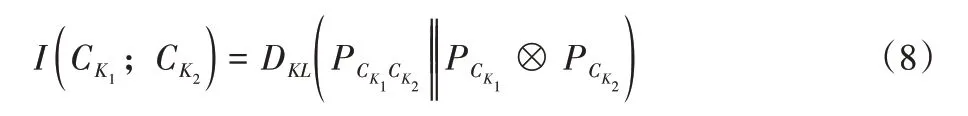
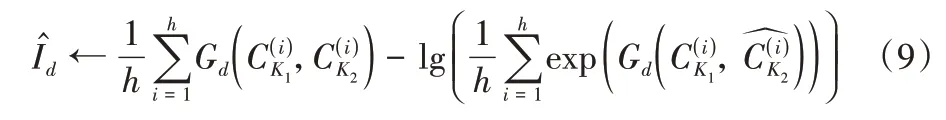
其中：Gd是具有参数d的聚合模块。为了计算下限，本文随机选择h张图像进行训练：首先，可以从K1和K2列中得到h对特征作为公共分布；然后，随机对在中的顺序进行置乱，得到h对特征作为计算边缘分布的结果；接着，将这些特性输入到聚合模块Gd中，通过式（9）得到交互信息估计的下限。使用移动平均法得到式（9）的梯度，通过最大化下限；接下来，更新聚合网络参数d←d+，近似地得到真实的交互信息。此外聚合模块也可以广泛应用于各种多列结构，作为一个分类器，它可以为多列结构识别不同尺度和分辨率的图像提供帮助，具有泛化性。

2 实验与结果分析

2.1 实验条件与数据集

本文实验使用显卡为NVIDIA GeForce GTX 1060 6 GB，内存为8 GB RAM，操作系统为Ubuntu16.04，编程环境为Python3.6 和Matlab2016a，配置为CUDA8.0 和CUDNN6.0，使用开源计算机视觉库Opencv2.0、深度学习框架选用Facebook 开源的动态神经网络框架Pytorch。

实验数据集为三个基准数据集ShanghaiTech［4］、UCF_CC_50（University of Central Florida Crowd Counting）［15］和UCSD（University of California San Diego）［16］。具体来说，ShanghaiTech（上海理工大学）数据集由Part_A 和Part_B 两部分组成。Part_A 是从互联网上收集的数据，有较高的人群密度；Part_B 是从繁华街道收集的数据，人群密度相对稀疏。UCF_CC_50 数据集主要包含较高密集人群的图像，背景噪声较大。UCSD 数据集是从真实的监控摄像头中采集的数据，具有低分辨率和稀疏的人群密度。

2.2 实验参数设置

将高斯分布的初始平均值设置为0，标准差设置为0.02。采用Adam 优化器对三列网络进行训练和优化，利用梯度的一阶矩估计和二阶矩估计，动态调整各参数的学习速率，学习率初始化为10-5。同时，将随机样本数h设为80，将动量设为0.9。采用ELU（Exponential Linear Units）激活函数更新各列参数，当输入信息小于0 时，为防止神经元坏死，通过斜率α的线性方程计算结果，α设置为0.95。

2.3 评价指标

依据前期工作［17-18］，使用平均绝对误差（Mean Absolute Error，MAE）和均方误差（Mean Square Error，MSE）评估模型性能，分别表示为：

其中：H是测试样本的总数；Zi是第i幅图像的真实值；是第i幅图像的估计值。MAE越小表示估计的准确性越高，MSE越小表示估计的鲁棒性越强。

2.4 实验有效性验证

2.4.1 UCSD数据集实验

如表1 所示，将本文算法与UCSD 数据集上的其他12 种先进算法进行了比较。其中CP-CNN（Contextual Pyramid Convolution Neural Network）和ic-CNN+McML（iterative crowd counting Convolution Neural Network Multi-column Multi-task Learning）较其他10 种算法有相对较好的效果，由此主要讨论它们的对比结果，CP-CNN 虽然比ic-CNN+McML 的MAE值高，即准确性能上相对较弱，但其MSE值比ic-CNN+McML低，说明其鲁棒性能更强，两种算法相比较各有优势。对比以上算法，本文算法在MAE值上与最优MAE表现的ic-CNN+McML 比较，减小了1.1%，优势不明显，但在MSE值上，本文算法相比ic-CNN+McML 有明显优势，相较于最优MSE表现的CP-CNN 减小了4.3%，也有一定优势。

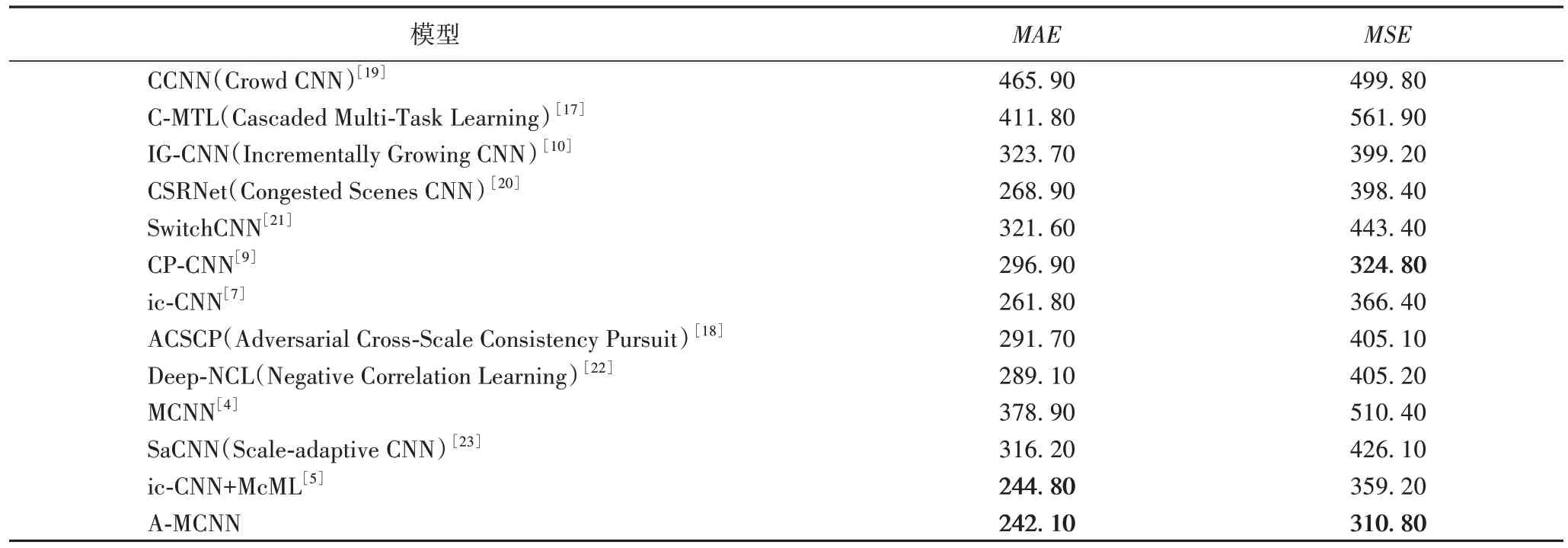
表1 UCSD数据集上的实验结果对比Tab.1 Comparison of experimental results on UCSD dataset

2.4.2 ShanghaiTech数据集实验

在ShanghaiTech 的两个子数据集ShanghaiTech Part_A 和ShanghaiTech Part_B 上测试本文算法。如表2 所示，将本文算法与ShanghaiTech 数据集上的其他12 种先进算法进行了比较。其中CSRNet 和ic-CNN+McML 整体相对其他10 种算法，在ShanghaiTech Part_A 和ShanghaiTech Part_B 上 的MAE和MSE值相对都较低且比较接近，更近一步比较这两种算法，ic-CNN+McML 在两个子数据集上的MAE和MSE值都略微比CSRNet 更小，但在ShanghaiTech Part_B 上的准确性几乎达到一致。此外，注意到ACSCP（Adversarial Cross-Scale Consistency Pursuit）在ShanghaiTech Part_A 上的MSE达到所有12 种算法的最优值，但其他数据都没有取得较好效果。对比以上先进算法，本文算法在ShanghaiTech Part_A 和ShanghaiTech Part_B 上都具有更低的MAE和MSE值，且与以上12 种算法中表现最好的ic-CNN+McML 比较，在ShanghaiTech Part_A 数据集上的MAE 比ic-CNN+McML 减小1.7%，MSE 比ACSCP 减小了3.2%，优势不明显；但在ShanghaiTech Part_B 数据集上的MAE和MSE分别比ic-CNN+McML 减小了18.3%、35.2%，具有明显准确性和鲁棒性优势。

表2 上海理工大学数据集上的实验结果对比Tab.2 Comparison of experimental results on ShanghaiTech datasets

2.4.3 UCF_CC_50数据集实验

在UCF_CC_50 数据集上测试本文算法。如表3 所示，将本文算法与UCF_CC_50 数据集上的其他9 种先进算法进行了比较。如表3 所示，除了CCNN 和SwitchCNN 有稍大的差异，其余各算法在该数据集上的性能差异不大，这与该数据集仅有50 张图像有一定关系。

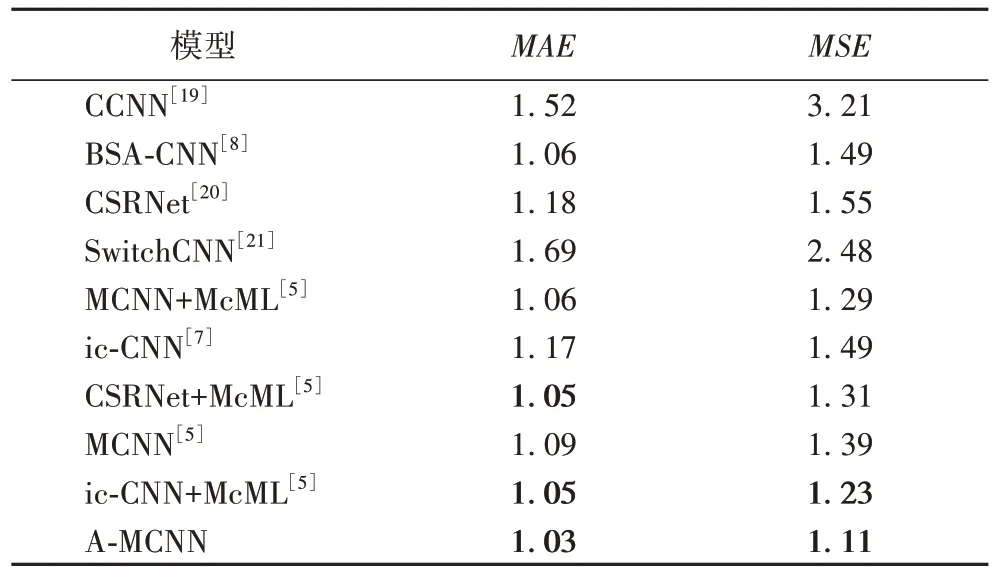
表3 UCF_CC_50数据集上的实验结果对比Tab.3 Comparison of experimental results on UCF_CC_50 dataset

更近一步比较各算法，CSRNet+McML 和ic-CNN+McML的MAE值较低，与此同时ic-CNN+McML 的MSE值也较低，这说明ic-CNN+McML 在该数据集上的整体性能效果相对其他所有算法更好。而本文算法A-MCNN 与ic-CNN+McML 的MAE值相比，比ic-CNN+McML 减小了1.9%，优势不明显，但A-MCNN 的MSE值却比ic-CNN+McML 减小了9.8%，鲁棒性能更强，优势更明显，A-MCNN 整体表现性能优于ic-CNN+McML。

从实验结果可知，A-MCNN 在各大基准数据集实验中，与对应数据集上其他先进的算法作比较，MAE值都有一定程度的减小，特别在MSE值上减小更明显，验证了该算法在提升准确性的同时，能够较大提升整个模型的泛化能力，更好适用于现实生活中各种复杂场景。

2.5 预估密度图可视化比较

如图3 所示，从公共基准数据集中选取5 张具有代表性的图像。第一张图，人口分布较均匀；第二和第三张图含有人群背景干扰，对人群计数准确性造成影响；第四、第五张图具有较大尺度变化，对人群计数是个很大的挑战。下面进一步从可视化角度分析输出单张估计密度图上的差异。如图3 所示，密度图为不同算法下对应左侧原图的预估密度图，各预估密度图中左上方数字代表对应原图的预估人数。

由图3 可看出，在ic-CNN+McML 和A-MCNN 对应的两列预估密度图中（图中方框标出），各个原图对应的两种算法下的预估人数较接近，也能近一步印证ic-CNN+McML 和A-MCNN 在准确性上的效果差异不明显，但通过定性实验发现A-MCNN 的准确性略微高于ic-CNN+McML，结合两个算法对应的预估密度图（黄色代表次高度密集，红色代表最高度密集），对比图中黄色和红色部分的深浅，A-MCNN 对应高度密集区域颜色更深，说明A-MCNN 在高度密集区域具有较高的敏感度和注意力。

图3 不同算法预估密度图的可视化Fig.3 Visualization of density maps predicted by different algorithms

2.6 图像像素值可视化

为了扩展人群图像特点的可视化效果，进行了人群像素值的分析。选择基准数据集中具有代表性的两幅图像进行实验，如图4 所示：一幅具有较规则的人口分布，另一幅具有明显的背景干扰和一定程度的尺度变化。使用Matlab2016a绘制两幅原图的像素值图，像素值图中x-y坐标代表图像长宽像素，图中像素柱对应原图有人区域，像素柱的高低代表该像素点处的像素值，人群越密集像素柱的值越高，如图4（d）中圈出区域。由于图4（a）中人口分布大体较均匀，对应的像素柱值的高度也大体较一致；由于图4（c）中右下角为背景区域，在像素图中相应位置无像素柱值，而原图左上角出现极度拥挤区域，相应地在像素值图中像素柱值越高。

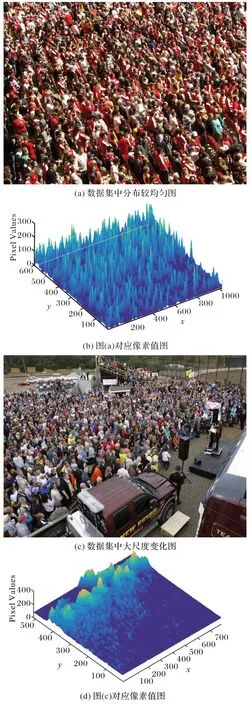
图4 图像像素值的可视化Fig.4 Visualization of pixel values of images

2.7 与经典目标检测算法对比

使用目标检测中经典算法Faster RCNN（Region Convolutional Neural Network）与本文算法进行实例对比实验。原图为成都理工大学下课拥挤画面抓拍图，分别在Faster RCNN 模型和本文算法上进行实验。

如图5（b）所示，Faster RCNN 目标检测时能对出现的完整个体或大部分完整个体标定识别，但针对图中方框中出现的高度密集人群几乎无法识别，检测效果不佳，可见Faster RCNN 更适合用于检测稀疏个体。如图5（c）为A-MCNN 检测结果，图最上方数字为预估人数，针对图5（a）中方框框出的高密度区域，能够通过密度图的高度密集反映，可见针对高度密集人群的检测，A-MCNN 比流行的目标检测算法Faster RCNN 更有优势。

图5 不同算法检测人群的结果Fig.5 Results of different algorithms to detect crowd

2.8 A-MCNN应用实例

选择在成都理工大学校园抓拍的三幅典型情况为例进行实验，如图6 所示：图（a）存在区域极度拥挤和雨伞遮挡情况，图（b）具有较大背景干扰，图（c）远近具有较大尺度变化。应用A-MCNN 算法得到预估密度图，最上方数字代表预估图像总人数。

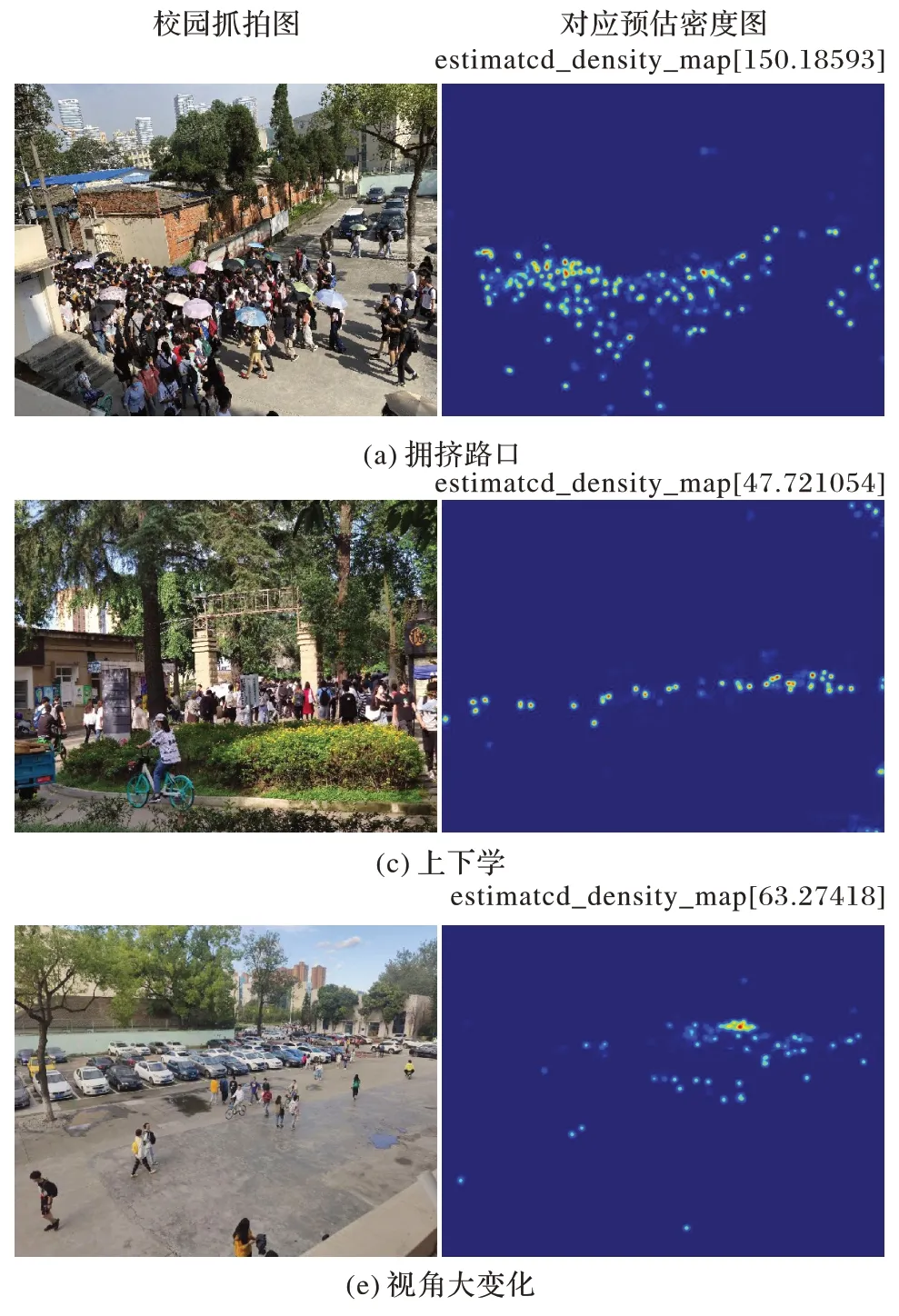
图6 A-MCNN应用实例Fig.6 Examples of A-MCNN application

3 结语

针对现有基于深度学习的人群计数网络中存在的大量冗余参数甚至过拟合导致输出精度下降的问题，提出基于多列卷积神经网络的参数异步更新算法A-MCNN，将其应用于尺度变化大及人群高度拥挤的复杂场景，对公共安全及疫情防控具有重要意义。实验结果表明，本文算法在不同数据集上应对场景突变、尺度变化、杂乱背景、光照影响、物体遮挡等影响检测精度的情况下，均能在准确性和鲁棒性能上获得较好的效果，为深度学习在人群计数上的应用提供了新方向。但是本文算法离实际应用场景实时性的需要还有差距，本文算法对于人群的检测采用的是每帧静态图像输入的方式，但实际场景需要做到实时视频检测，还需考虑视频前后帧的时序信息和处理视频数据的速度，提升算法实时性，同时未来应重视整个模型前后端处理以更加轻量化整体模型、改善物体遮挡问题将也是主要研究方向。