单双点平滑结合的流形正则化半监督分类学习框架
2022-07-07沈雅婷
沈 雅 婷
(南京理工大学紫金学院 江苏 南京 210023)
0 引 言
全监督学习需要拥有大量的已标记实例,但在现实中获取未标记实例不困难,通过手工标记实例却很难。半监督分类框架研究是机器学习中最受欢迎的领域之一,因为它利用少量的已标记实例的同时也可以运用未标记实例的信息。
半监督分类中两个常见的假设,聚类假设[1]和流形假设。基于图的半监督分类方法,例如标签传播[2]、图切割[3]和流形正则化(MR),这些都是采用流形假设。
基于图的半监督分类方法中除了MR,基本都是直推式方法[4]。MR是一种能够预测测试样本的归纳方法[5]。
实例的分类输出应该在流形图上平滑。但是平滑是如何实现的呢?在学习中,MR遵循流形假设,流形假设约束流形图上的相似实例应该共享相似的分类输出[6]。MR将视每个实例对为单位。因此,它是建立在流形图上的双点平滑上的。然而,平滑在本质上是以单个实例为单位的,也就是说,平滑性应该发生在“任何地方”,通过将每个单点行为与其近邻的行为联系起来。虽然在一些研究中认为单点平滑是合理的,但在具有流形假设的MR中,它和双点平滑还没有同时实现。一种新的框架是单双点平滑结合的MR(SDS_MR),通过结合实例对约束[7]和单点局部密度来实现半监督学习。通过这种方法,保留了单双点的光滑性,它们都具重要性且都可作出贡献。本文以实例对的约束信息和单个实例的局部密度[8]为例,当然,这一想法也可以应用到其他框架中。对于此问题的解决,SDS_MR的公式与MR的公式相似,因此求最优解步骤也是相似的。最后在UCI数据集上的实证结果显示,SDS_MR与MR相比具有一定的竞争力。
为了更好地预测效果,近期有研究表明[9]对MR的改进,获得或多或少的改进效果。事实上,本文提出的SDS_MR框架也可以引入到这些改进中,有望进一步提高预测的有效性。
1 相关工作
1.1 流形正则化半监督分类框架(MR)
流形假设是半监督学习中最常用的数据分布假设之一,它假设流形结构上的相似实例应该共享相似的分类输出。MR是一种半监督分类框架,它就是运用了流形假设进行深入研究的,近年来应用到各种领域中。
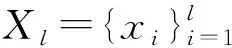
(1)
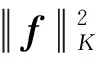
(2)
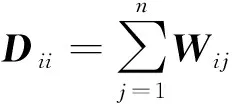
(3)
式中:K:X×X→R是一个Mercer核[14]。
1.2 双点平滑
双点约束可以通过将实例的标签转换为双点约束来改进模型中包含的信息。在一些实际应用中,只会提前得到实例的一些标签之间的关系,然后可以将这些标签转换为双点约束信息来训练半监督模型。
具体而言,如果两个已标记点的标签是相同的,它们就是双点可关联约束,构成必要的关联集MS;同理,如果两个已标记点的标签不同,则它们就是双点不可关联约束,构成不可能的关联集CS。假设分类决策函数为f(x),那么所有实例的预测值可以表示为f=[f1,f2,…,fn]T∈Rl×n,那双点约束可以表示如下:
(4)
式中:i,j,p,q∈[1,n]是数据集中实例的序号;〈i,j〉表示在集合MS中任何必要的双点关联约束;〈p,q〉表示在集合CS中任何不可能的双点关联约束;|·|表示集合MS或者集合CS中的双点约束的数目。
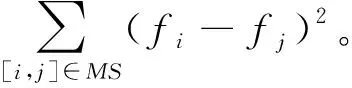
矩阵Qn×n的元素定义如下:
(5)
通过矩阵表示可以写为:
(6)
U=H-Q
(7)
式中:H=diag(QL),L是一个维度是n×1的向量并且它的元素都为1。
2 单双点平滑结合的半监督流形正则化分类框架(SDS_MR)
MR采用双点平滑约束流形图上的相似实例共享相似的分类输出。在本节中,提出一个单双点平滑结合的MR框架,利用双点平滑约束和单点局部密度。
2.1 算法框架
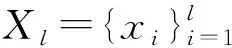
(8)
式中:第三项的后半部分表示双点平滑约束。τ是参数,用来平衡式(8)中第三项中的两部分。当τ=0,SDS_MR将退化成MR。在式(8)中第三项的前半部分,N(xi)是xi的近邻集,xj在xi的近邻集中。p(xi)表示实例xi的局部密度,它可以根据实例与其近邻点之间的归一化距离来计算,数值越小表示实例周围分布越密集。但是,当实例xi在两个类别的重叠区域,根据上述的局部密度,在xi的周围会很密集。因此,在式(8)第三项的前半部分,xi将被赋予更大的重要性或更大的惩罚,但是仍然这是不可预期的。因此在计算单点局部密度时,不仅会考虑近邻密度,还会考虑无监督学习结构[15]。
(9)

式(1)中第三项是对双点具有平滑惩罚的正则化项[16],式(8)中的第三项与其不同,它同时考虑了双点平滑和单点平滑。
进一步将式(8)中的第三项写成:
2(τ(fTLPWf)+(1-τ)(fTLf))
(10)

SDS_MR框架通过采用不同的损失函数生成不同的分类器。接下来,分别使用平方损失函数[17]和铰链损失函数[18]为上述框架推导单双点平滑结合LapRlsc和单双点平滑结合LapSVM。
2.2 单双点平滑结合的Laplacian正则最小二乘法(SDS_LapRlsc)
利用平方损失函数,SDS_LapRlsc的公式可写为:
(11)
它可以写成:
(1-τ)(fTLf)]
(12)
应用Representer定理后,式(12)问题的解可由以下形式表示:
(13)
继续优化函数可以表示成:
(14)
式中:α=[α1,α2,…,αl+u]T是拉格朗日乘子向量[19]。Kl=(Xl,X)H∈Rl×(l+u)和K=(X,X)H∈R(l+u)×(l+u)是核矩阵,其中Xl表示已标记数据集,X表示整个数据集。已标记数据的类标签向量用Yl=[y1,y2,…,yl]T表示。
通过J1对α求导后值为0求最小值,因此:
(1-τ)(KLKα)]=0
(15)
最后,得到:
(16)
2.3 单双点平滑结合的Laplacian支持向量机(SDS_LapSVM)
应用铰链损失函数,SDS_LapSVM的公式可写为:
(17)
ξi≥0,i=1,2,…,l
进一步写为:
(1-τ)(fTLf)]
(18)
ξi≥0,i=1,2,…,l
应用Representer定理之后,即式(13)可以得出:
(1-τ)(αTKLKα)]
(19)
ξi≥0,i=1,2,…,l
应用拉格朗日乘子法后,得到:
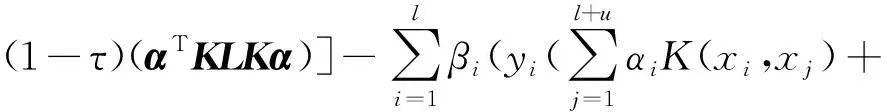
(20)
式中:βi是拉格朗日乘子。
进一步得出:
(21)
因此,再将J2写成:
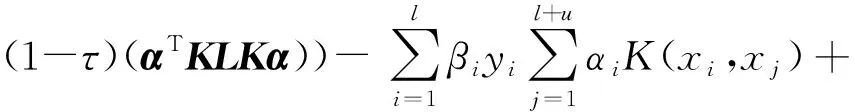
(22)
式中:J=[I0]是一个维度为l×(l+u)的矩阵(假设前l个点是已标记),其中I是维度为l×l的单位矩阵,并且Y=diag(y1,y2,…,yl)。
进一步得到:
(1-τ)(KLKα))-KJTYlβ=0
(23)
因此有:
(24)
将式(24)代入到简化的式(22)中,可以得到:
(25)
其中:
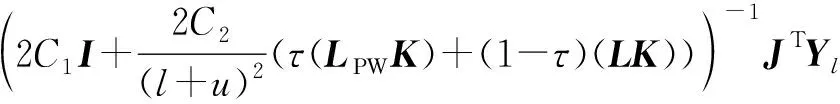
(26)
3 实验与结果分析
本节将评估SDS_MR在13个UCI数据集上的性能,并与MR进行比较。表1给出了UCI中13个数据集的相关信息。每个数据集被随机分成两部分,分别用于训练和测试。训练集分别包含10个和100个已标记样本供选择。然而,若选择包含100个已标记样本,但是训练样本数量却小于100,那么只选择其中一半的训练样本作为已标记样本。重复数据划分和训练过程20次并记录其平均精确度和标准差。
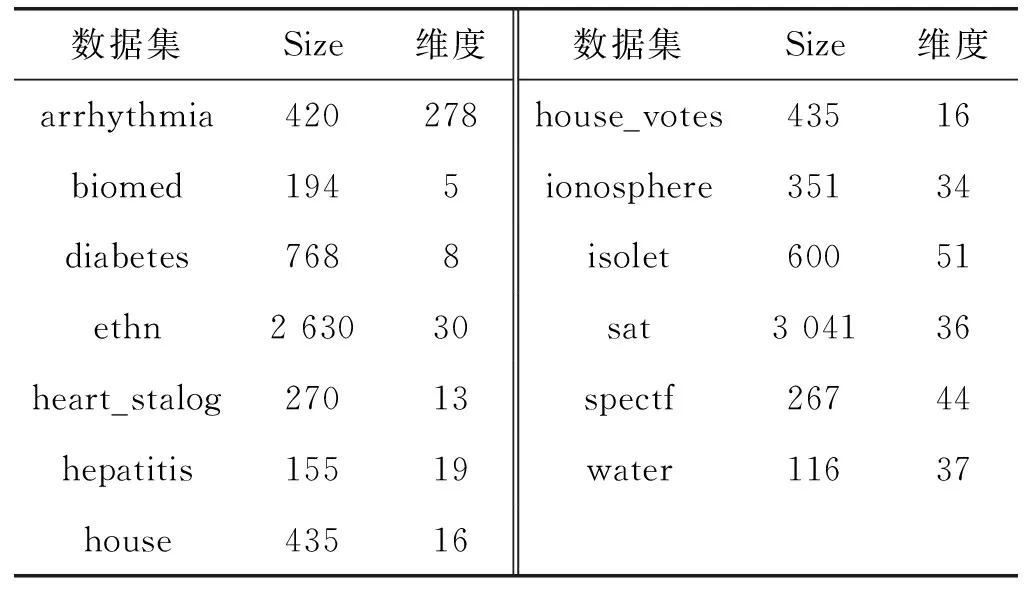
表1 13个UCI数据集的相关信息
在比较实验中使用的是线性核。在MR和单双点平滑结合MR的图构建中,近邻数k都被简单地设置为10。当已标记样本数为10时,记录最佳性能时的所有正则化参数组合值,当已标记样本数为100时,通过五折交叉验证[20]选择出正则化参数组合值。其中参数τ值设为0.5,参数C1和C2的取值范围为{0.01,0.1,1,10,100}。
3.1 性能比较
表2和表3分别给出了在具有10个和100个已标记样本的UCI数据集上的比较结果。每行给出了每个方法在对应数据集上的性能,并且最后一行给出了每个方法在所有数据集上的平均性能。此外,在每一行中,加粗数值表示在此数据集上的最佳精确度,并且斜体数值表示在此数据集上SDS_LapRlsc/SDS_LapSVM的性能优于LapRlsc/LapSVM。
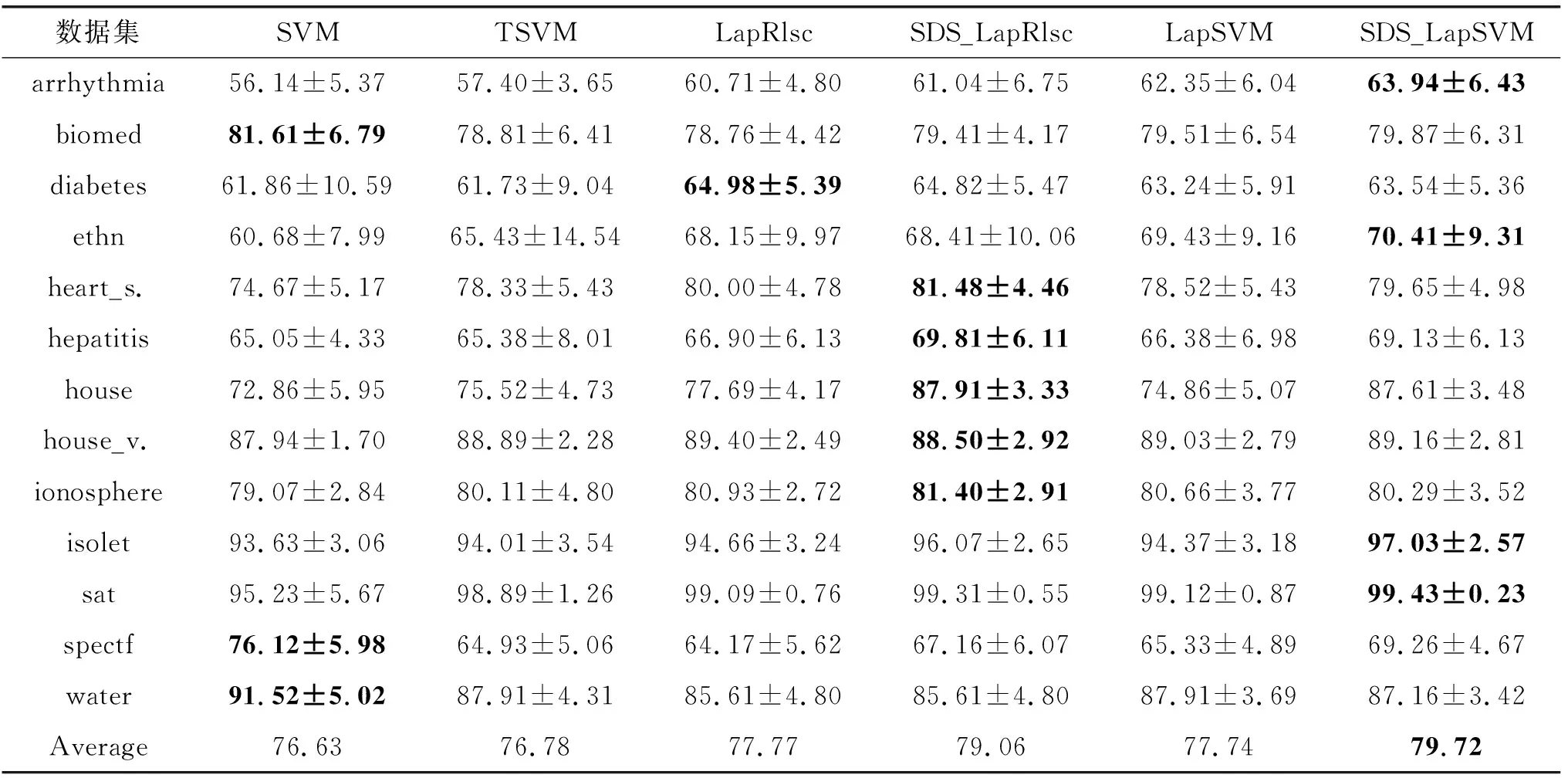
表2 具有10个已标记样本的UCI上的精确度(%)

表3 具有100个已标记样本的UCI上的精确度(%)
从表2和表3中,可以分析得到以下结论:
(1) 当已标记样本数为10时,一共13个数据集,SDS_LapRlsc在其中12个数据集上的正确率高于LapRlsc,SDS_LapSVM在其中11个数据集上的正确率高于LapSVM。当已标记样本数为100时,SDS_LapRlsc在其中7个数据集上的正确率高于LapRlsc,SDS_LapSVM在其中8个数据集上的正确率高于LapSVM。因此,通过单双点平滑结合,可以提高半监督分类学习的正确率。
(2) 当已标记样本数为10时,在9个数据集上,表现最好的不是SDS_LapRlsc就是SDS_LapSVM,当已标记样本数为100时,在6个数据集上,表现最好的不是SDS_LapRlsc就是SDS_LapSVM。因此,与其他优秀的半监督分类方法进行比较,提出的单双点平滑结合MR确实具有优势。
(3) 当已标记样本数为10时,在3个数据集上,全监督SVM的表现优于半监督分类方法,当已标记样本数为100时,在3个数据集上,全监督SVM的表现优于半监督分类方法。从而得出,在某些情况下,半监督分类学习可能是不安全的,比对应的全监督方法表现更糟。因此,设计性能不会比相应的全监督方法差的单双点平滑结合MR安全学习策略是一项重要工作。
(4) 当已标记样本数为10时,也就是说已标记样本更少时,单双点平滑结合MR的性能改进更明显。原因可能是已标记信息越少时(这里是10和100比较),半监督学习越有利,因为改进的空间更大。此外,通常必须要处理具有极有限已标记样本的半监督分类任务,因此,单双点平滑结合MR的性能改进值得期待。
3.2不同参数τ值的性能表现
参数τ对于单双点平滑结合MR的性能表现很重要,因此,这里展示在6个UCI数据集上具有不同τ值的SDS_LapRlsc的性能表现,并以SVM作为基准。每个UCI数据集只包含10个已标记样本。采用线性核并且τ的取值范围为{0,0.25,0.5,0.75,1}。最后,得到结果如图1所示。
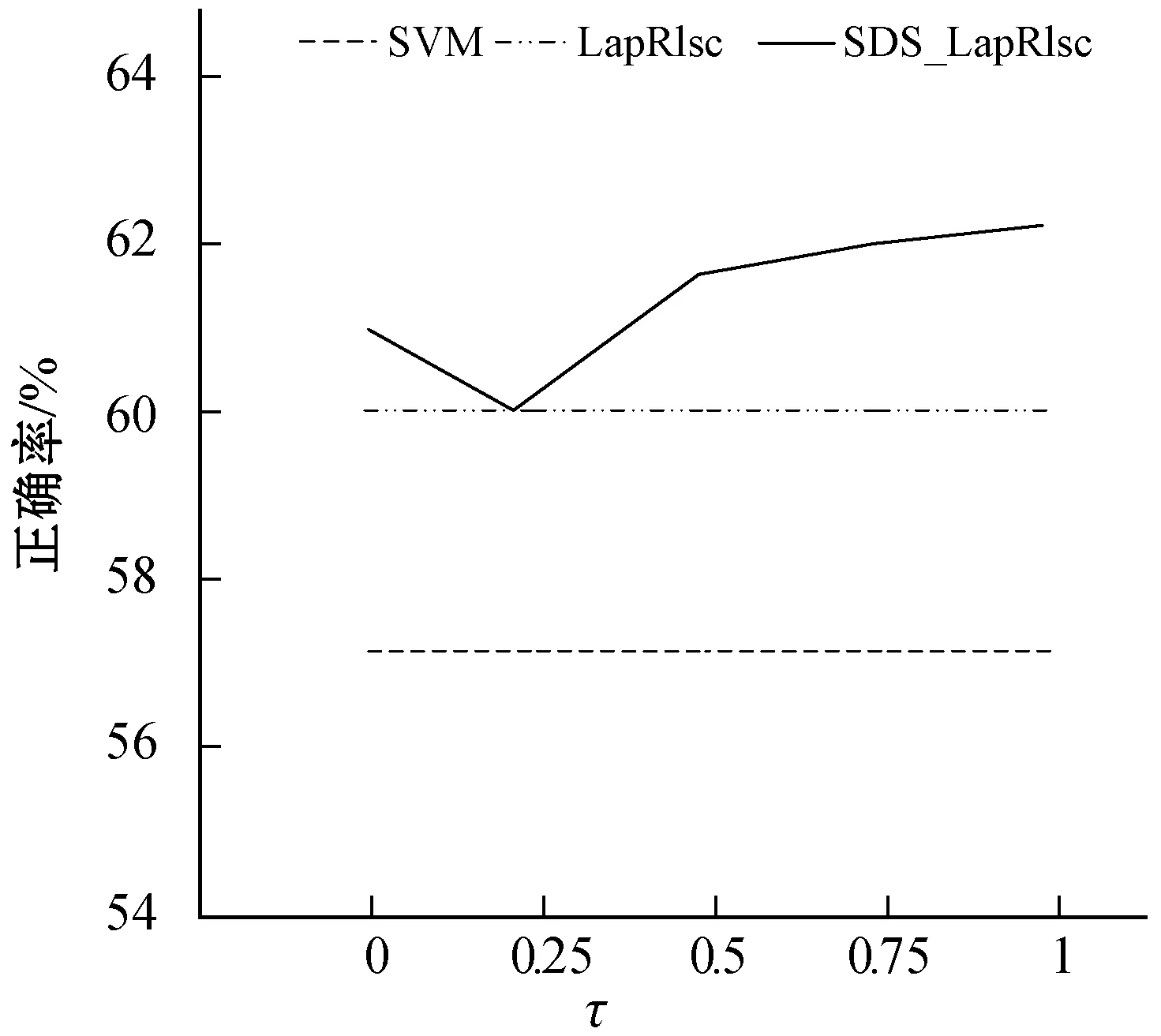
(a) arrhythmia

(b) biomed
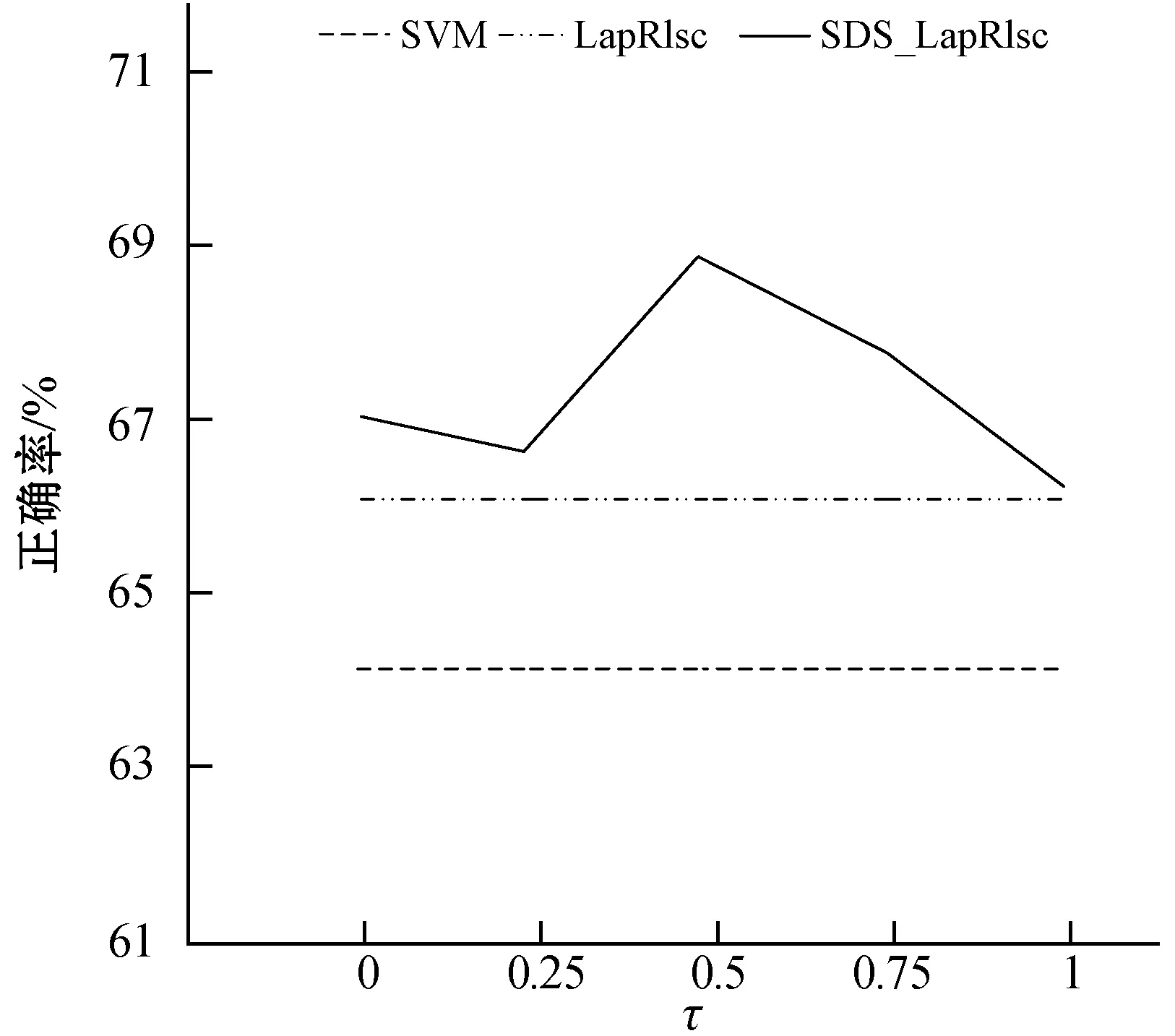
(c) hepatitis

(d) house
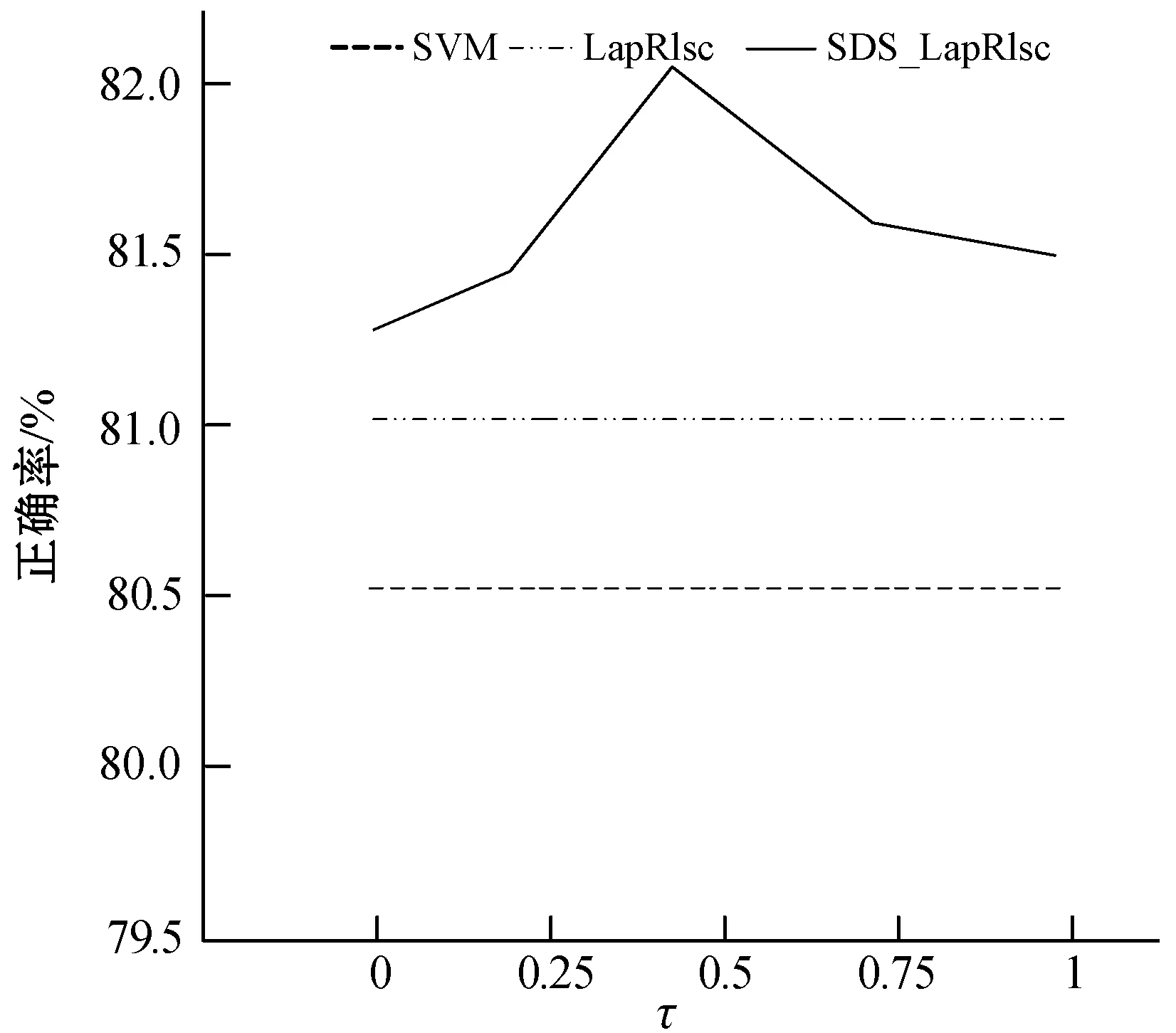
(e) ionosphere
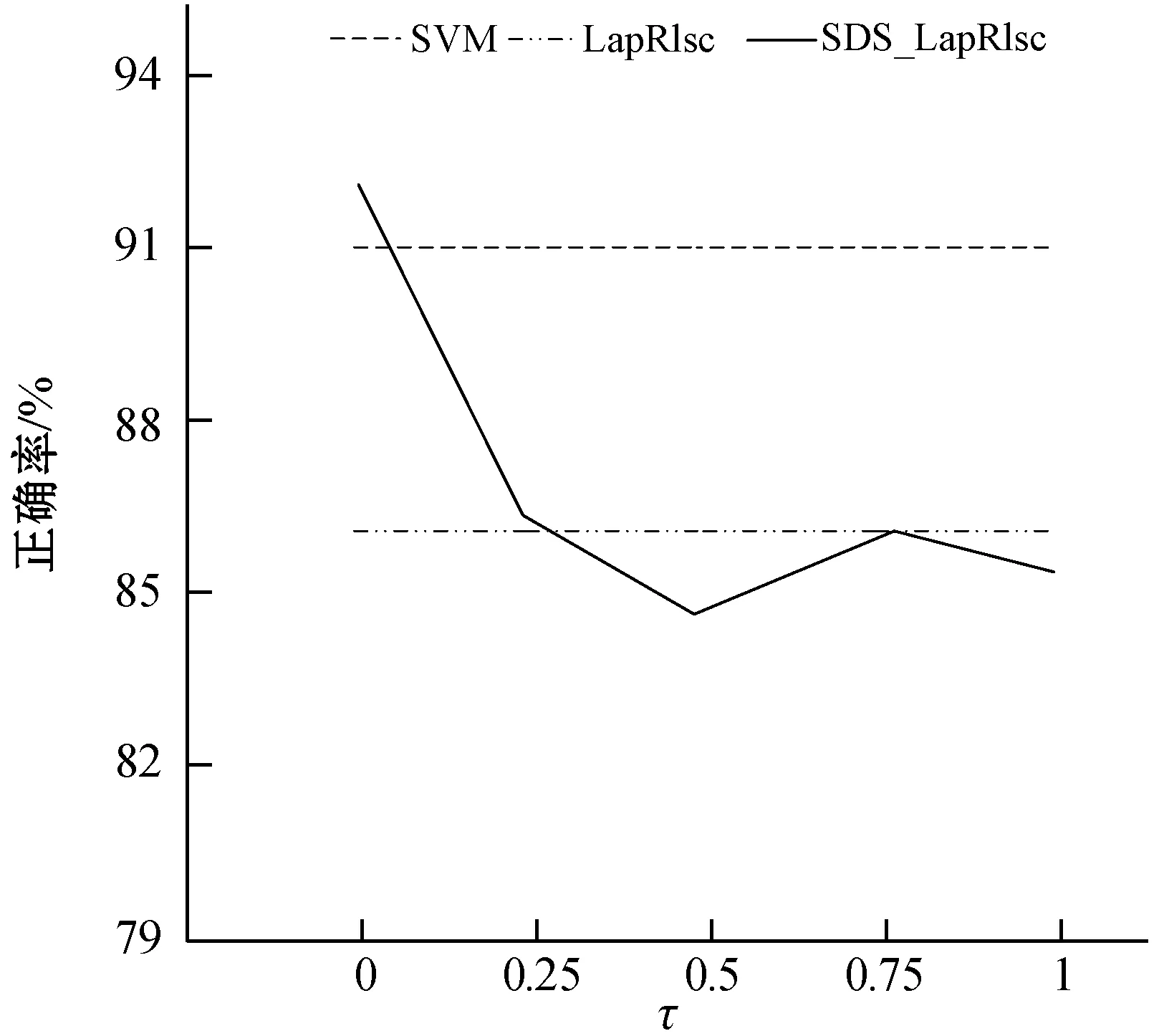
(f) water图1 不同数据集上SDS_LapRlsc的性能表现图
从图1中,可以分析得到以下结论:
(1) 在单个数据集上的性能变化规则是不同的。具体来说,在大多数数据集上,当τ取值为0.5时可以获得满意的性能,要选择最合适的τ很难,这也将是未来一项重要工作。然而,即使将数值τ固定为0.5,SDS_LapRlsc的性能已经具有竞争力了。
(2) 当τ取不同的值时,SDS_LapRlsc的性能通常优于LapRlsc,说明SDS_LapRlsc的健壮性。因此,当τ取适当的数值时,SDS_LapRlsc能够提供非常优秀的分类性能。即使将τ固定为0.5,单双点平滑结合MR也比MR更具优势。
4 结 语
在给定构造流形图上,实例的分类输出在图上是希望平滑的。但这种平滑是如何实现的呢?在学习中,MR实际上采用了流形假设,它视每个实例对为单位,并约束流形图上的相似实例应该共享相似的分类输出。因此,它是建立在流形图上双点平滑约束。其实平滑在本质上是以单个实例为单位的,通过将每个单点行为与其近邻的行为联系起来。因此,本文提出一种新的框架是单双点平滑结合的MR(SDS_MR简称)。最后,对UCI数据集的实证结果表明,SDS_MR与MR相比具有竞争力。为了更好地预测效果,本文提出的结合单双点的平滑性方法可以尝试引入到其他学者提出的改进的MR算法中,甚至将结合单双点的平滑性方法应用到其他先进的分类框架中,有望进一步提高预测的有效性。
