Python在运筹学教学中的应用

肉孜买买提·马合木提

[摘           要]  分析當前运筹学实验课的发展趋向，把Python语言结合到运筹学规划问题上来，通过Pulp 和 Tkinter模块设计了可以简单地求规划问题（包括整数变量、0-1变量）最优解的界面。

[关    键   词]  运筹学;线性规划;Python;Tkinter

[中图分类号]  G642                    [文献标志码]  A                  [文章编号]  2096-0603（2022）06-0088-03

一、引言

（一）规划问题

运筹学是一门系统性的应用型科学，提供决策目标和数量分析[1，2]。运筹学包括线性规划、运输问题、整数规划、混合线性规划、目标规划和动态规划等。运筹学原来以讲授理论为主，随着计算机科学技术在各领域中的应用变强，运筹学应用也得到极大的促进。在这种情况下，开设运筹学试验课是大势所趋。

最近国内运筹学试验课程得到巨大的发展，目前常有的运筹学试验软件有Lingo[3]、Matlab[4]和Excel[5]。其实Python对运筹学的应用也是强大的，但是此方面的研究较少。本文介绍Python语言在运筹学试验教学中的应用，尤其是在线性规划、整数规划和混合线性规划中的应用。

（二）Python语言

Python是一种面向对象的、解释性的高级程序设计语言。当前Python与高校专业课程内容的融合变得十分重要[6]。Python是简单易学，非常适合初学者，而且包含丰富的库，目前最接近自然语言的编程语言[7]。其中的Tkinter模块在界面可视化工程中得到编程者的喜爱。本文首先介绍Tkinter模块，且通过Tkinter模块造出可视化界面，应用于线性规划、整数规划和混合线性规划中，提高学生解决实际问题的能力。

Tkinter是Python的标准GUI库，由于简单而好学，在程序界面设计工作中受编程者的喜好[8]。因为Tkinter是Python的标准库，因此编程过程中只需用import Tk-inter来调用即可。详细内容请见参考文献[8]。

二、主要技术实现过程

（一）模块的安装

本文将使用以下扩展库：

-numpy：针对存储和处理高维数组和矩阵运算

-Tkinter：GUI设计

-sympy：符号运算和矩阵运算

-Pulp：求解线性规划包（可以处理整数规划问题）

下面介绍各模块的下载和安装。Windows 7或Win-dows 10中先按Window+R，并运行cmd，并输入

pip install Pulp

pip install numpy

pip install sympy

命令进行安装。

（二）实现过程

首先通过以下代码可以建立我们的界面。

from tkinter import Tk

root = Tk（）

root.title（"混合线性规划"）

root.geometry（′800 × 430′）

root.resizable（width = False，height = False）

zsWindow（root）

root.mainloop（）

其中，zsWindow（）是一个类，被定义为

class zsWindow：

         def __init__（self，root）：

                  # 创建一个下拉列表

                  self.max_min = StringVar（）

                  self.numberChosen = ttk.Combobox（root，

                            font=（′Arial′，13），width=12，

                            textvariable=self.max_min）

                  # 设置下拉列表的值

                  self.numberChosen[′values′]=（′max′，′min′）

                  self.numberChosen.place（x=50，y=30，

                            height=30，width=120）

                  self.numberChosen.current（0）

                  self.numberChosen[′state′] = ′readonly′

………

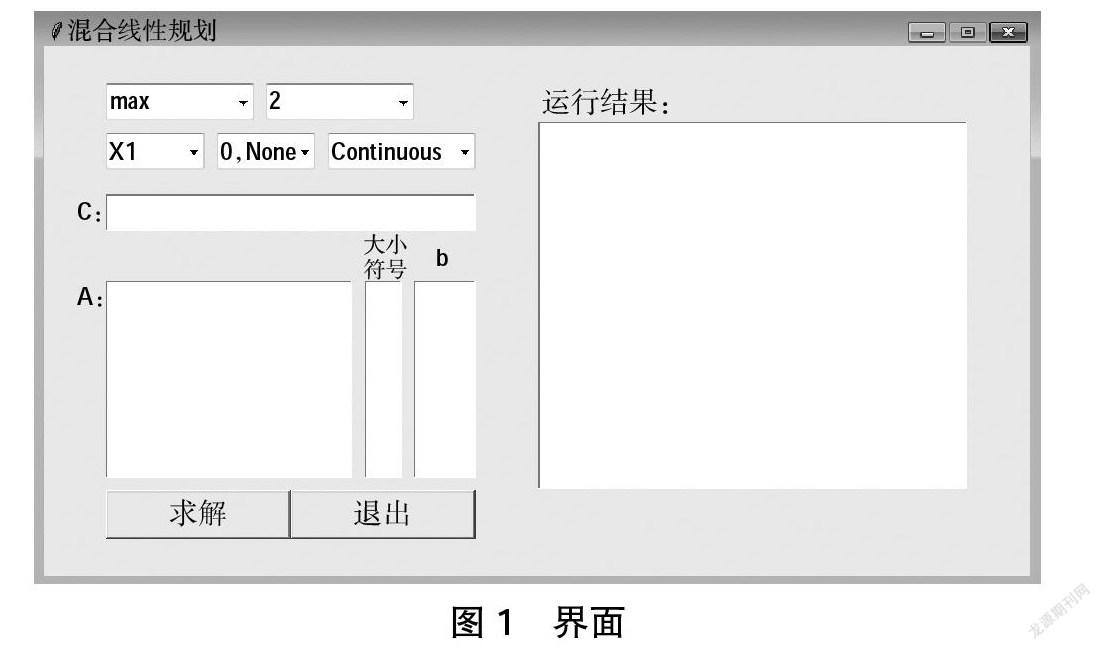
代码包括100多行，本文中忽略剩下代码。得到的窗口为图1所示。

界面中左上的第一个下拉单中可以选择“max”或“min”，表示该问题是最大值问题或者最小值问题。右边的下拉单中可以选择该问题中的变量数。下面三个下拉单中可以设置变量的取值范围和整数性。在默认状态下变量的取值范围为非零数和一般连续变量。变量也可以设置为“Integer”，表示该变量为整数变量，也可以设置为“Binary”，表示该变量为0-1变量。因此，此界面可以求一般线性规划问题、整数规划问题和混合规划问题的解。文本框A、b、c分别为系数矩阵、条件系数和目标系数。大小符号框只能输入“>、<或=”符号，如果放空，就默认识别为“<”符号。求解按钮通过以下命令设置：

#命令按钮

self.But1 = Button（root，font=（′Roman′，13），text=＼

             "求解"，command = self.do_job_Button）

self.But1.place（x=50，y=360，width=150，height=40）

其中do_job_Button函数被顶以为：

def do_job_Button（self，ev=None）：

       c = self.var.get（）

       c_list = c.split（）

       self.lb1.delete（0，END）

       #如果输入内容不是数字出现错误框

       try：

self.c = np.array（c_list，dtype=float）

       except：

messagebox.showerror（title=′Error Message′，

message = ′輸入有错误！′）

return

        #如果c的长度与变量数不一致

        if len（self.c） ！= self.v_num：

            messagebox.showerror（title=′Error

      Message′，

        message=′c的长度与变量数不一致！′）

        return

……………………

res = self.Linear_Op（objective ，constraints）

#输出结果

self.lb1.insert（END，′最优解为：′）

self.lb1.insert（END，′      ′ + str（res））

#若最优解存在，则输出目标函数值

if （self.status == 1）：

  self.lb1.insert（END，′最优目标函数值为：′）

self.lb1.insert（END，′      ′+＼ str（np.dot（self.c，res）））

按“求解”按钮后召唤do_job_Button函数。首先读取所有信息，并转换成数组。如果输入有误会自动报错。读取信息后，执行“Linear_Op”函数。“Linear_Op”函数被定义为：

def Linear_Op（self，objective，constraints）：

        #确定最大化问题还是最小化问题

        if self.max_min.get（） == ′max′：

                 maxmin = pulp.LpMaximize

        else：

maxmin = pulp.LpMinimize

       #創建线性规划问题

       prob = pulp.LpProblem（′LP1′，maxmin）

       prob += objective

       for cons in constraints：

               prob += cons

       lb_list = str（prob）.split（′＼n′）

       self.status = prob.solve（）

       if self.status == -1 ：

               return ′无可行解′

       elif self.status == -2 ：

               return ′无界解′

       else ：

               return [v.varValue.real for v in＼

               prob.variables（）]

（三）举例操作

例题1.求下面规划问题的最优解

s.t.max z = 12x1+6x2+3x32x1+3x2-4x3>-9x1+5x2+x3<10x1≥0，x2∈R（整数），x3：0-1变量

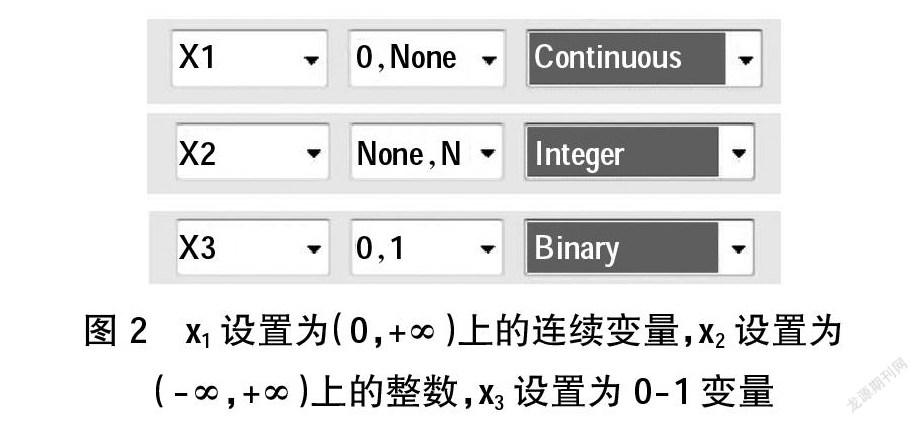
首先该问题是最大值问题，包括三个变量（三个变量的设置如图2所示）。

图2 x1设置为（0，+∞）上的连续变量，x2设置为

（-∞，+∞）上的整数，x3设置为0-1变量

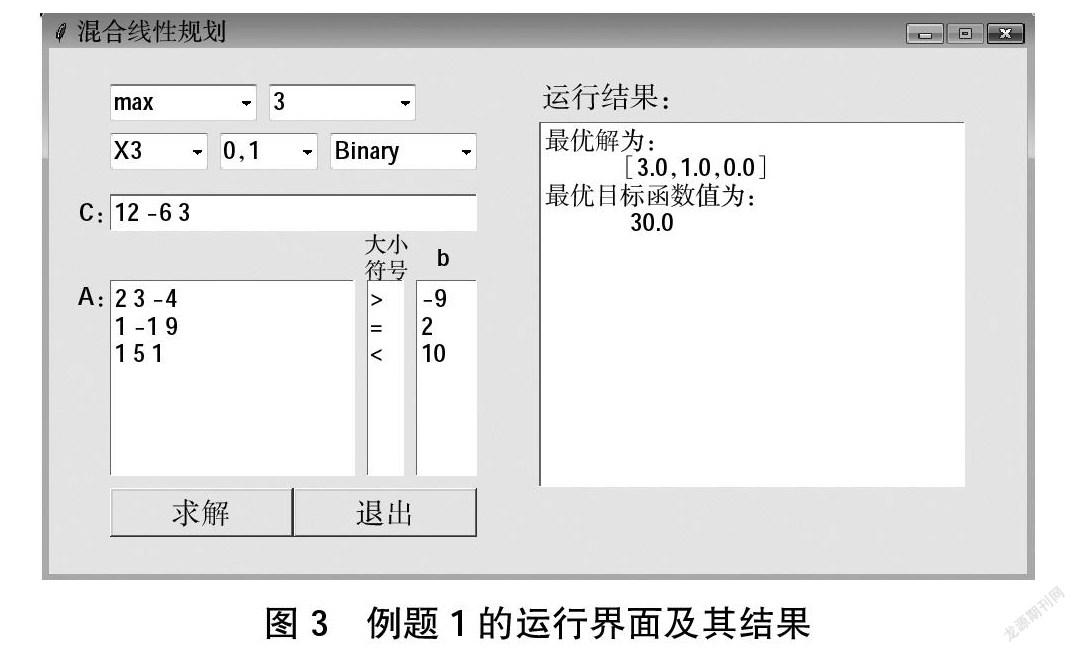
具体输入方法和运行结果如图3所示。

最优解为（x1，x2，x3）=（3，1，0），最优值为z=30。

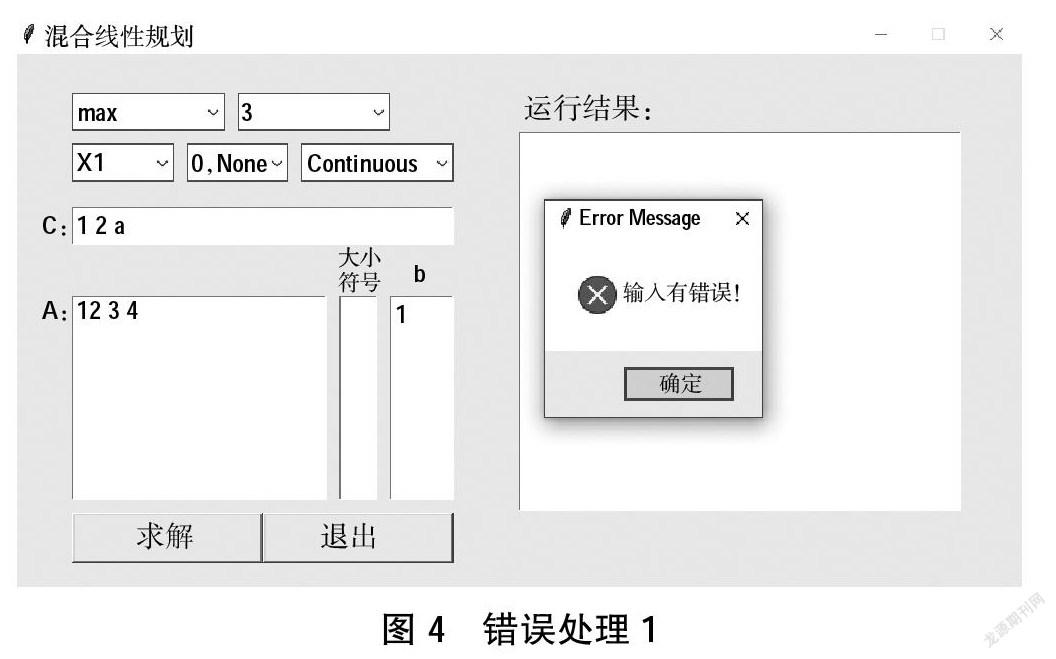
本程序可以用if语句、ry-excep语句和message-box.showerror函数报错误，如果向量c中包含“字符”，则可以通过以下代码达到图4的效果。

#如果输入内容不是数字出现错误框

try：

      self.c = np.array（c_list，dtype=float）

except：

      messagebox.showerror（title=′Error Message′，＼

      message=′输入有错误！′）

    &nbsp; return

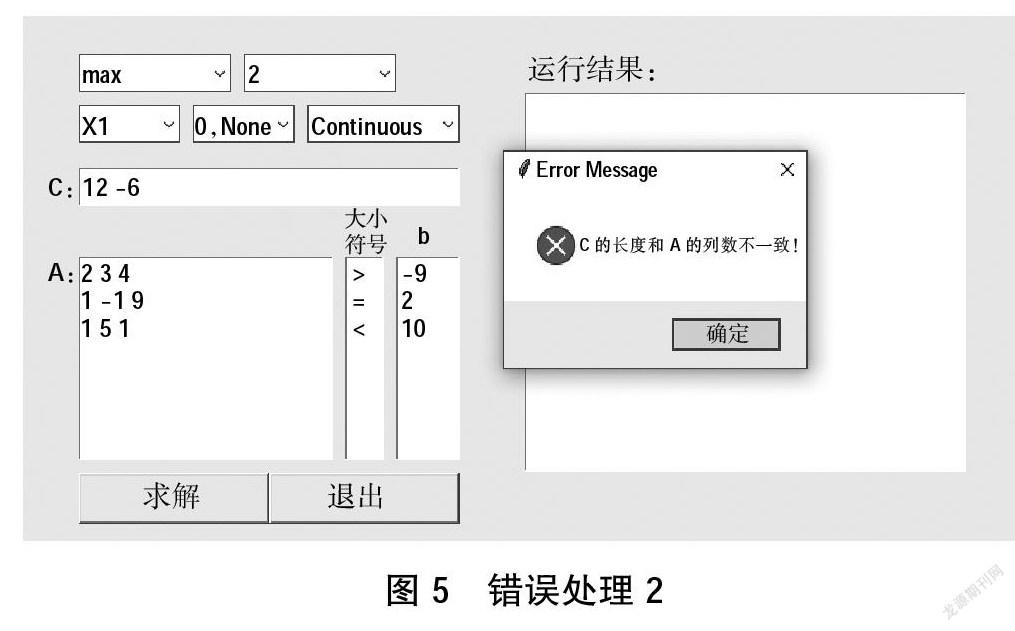
如果向量c的长度和矩阵A的列数不一致，则

#如果c的长度与变量数不一致

if len（self.c） ！= self.v_num：

messagebox.showerror（title=′Error Message′，＼

message=′c的长度与变量数不一致！′）

      return

三、结论

本文我们通过Tkinter模块，简单地构造了界面，并用Pulp模块求规划问题的最优解。使用起来方便、简单，可用于线性规划问题、整数规划问题和混合问题，效果良好。在编程和使用此界面过程当中使学生会掌握Python基础语言、Tkinter和Pulp模块的使用。同时也可分辨出线性规划、证书规划和混合问题之间的区别。对提升教学质量和培养学生的学习热情起很大的作用。其实动态规划和目标规划问题也可以通过本文构造的界面解决，但需要先建立问题的规划模型。下一步要构造出能方便地解决运输问题、目标规划等规划问题的界面。

参考文献：

[1]运筹学教材编写组.运筹学[M].北京：清华大学出版社，2005.

[2]胡运权.运筹学基础及应用（第六版）[M].北京：高等教育出版社，2014.

[3]丁小妹，王平.Lingo软件在运筹学实验教学中的应用[J].武夷学院学报，2017（9）：108-110.

[4]张明，王文文.Matlab在经管类运筹学教学中的探索与实践[J].大学教育，2012（7）：81-89.

[5]于瑛英.EXCEL在运筹学规划论教学中的应用[J].教育教学论坛，2014（10）：278-280.

[6]嵩天，黄天羽，礼欣.Python语言：程序设计课程教学改革的理想选择[J].中国大学教学，2016（2）：42-47.

[7]毛焱颖，张羽，焦柳丹.Python语言程序设计课程教学实践[J].电子技术，2021（50）：76-77.

[8]高秀艳.基于Tkinter的多语语料库分段与对齐工具实现研究[J].河北软件职业技术学院学报，2020（22）：5-8.

◎编辑 马燕萍