可信区块链隐私计算平台研究与实现*

胡绍洲，马兆丰，叶可可

（1.北京邮电大学 网络空间安全学院，北京 100876；2.中移动信息技术有限公司 研发创新中心，北京 102200）

0 引言

随着大数据、人工智能和云计算等技术的快速发展，产生了很多新的服务，需要采集用户的相关信息，但对这些敏感信息的分析和利用可能导致用户隐私的泄露，给用户带来巨大的安全风险，因此，针对敏感数据的隐私计算需求已成为社会共同关注的焦点。如今，隐私计算技术深度融合多方安全计算、可信执行环境、联邦学习等技术，为可信计算、金融、医疗、大数据、电子拍卖等领域的数据流通域中数据的“可用不可见”提供了有效的解决方案[1]。

但目前隐私计算技术只能提供数据的“可用不可见”特性，因此如何保障隐私计算体系中数据源和数据隐私计算结果的真实性，成为隐私计算发展的重要方向。目前隐私计算在金融、互联网、公共服务、数字版权及保险领域都有了广泛应用[2]。

区块链技术为隐私计算的数据源流通过程中的不可篡改提供了技术保障。区块链技术是一种按照时间顺序将数据区块以链条的方式组合成特定数据结构，并以密码学方式保证的不可篡改和不可伪造的去中心化总账（Decentralized Shard Ledger），能够安全存储简单的、有先后关系的、能在系统内验证的数据[3]。目前的电子拍卖市场还处于初级发展阶段，存在参与方多、数据难以协同和各方信任缺失的特点。因此在招标式电子拍卖时，拍卖者对于自身出价金额需要进行个人隐私保护，拍卖人只需要公布结果，而不需要公布拍卖者的具体金额，可以采用隐私计算的方式计算出出价最高者，保护被拍者并对保留价进行出价，同时对招标结果的隐私计算过程进行上链操作，实现电子拍卖全流程的可追溯性。

1 相关工作

互联网信息时代赋予了商品新的交易形式，如电子交易和电子拍卖等，也增加了交易的安全风险和隐患，在人们进行电子交易和电子拍卖的过程中，窃取个人隐私数据的行为与日俱增[4]。

随着区块链的去中心化特性被广泛采用，工商银行在区块链隐私计算融合技术方面开展了相关探索和实践，建设了以区块链技术和隐私计算技术为支撑的区块链联盟计算平台[5]。使用区块链技术对敏感数据隐私计算后的结果进行上链存证，保证了数据源的不可篡改性和可溯源性。

Xue[6]将区块链技术应用于企业财务信息融合共享系统，形成了公司间的企业财务信息融合共享体系，改善了当前财务共享平台的局限性和弊端。Biswas等人[7]提出了一种使用区块链的无欺骗门限秘密共享方案，该方案基于Shamir技术，消除了由于工作量证明/权益证明（Proof of Work/Proof of Stake，PoW/PoS）共识导致的漏洞，并成功解决了股票欺骗问题。为了保护电子拍卖中竞拍者的身份隐私，王小丽等人[8]提出了一个基于匿名通信的匿名电子拍卖协议，该协议在密封式拍卖方式的基础上，采用匿名通信模型进行通信。

为了解决在电子拍卖场景下拍卖策略、拍卖金额的隐私安全问题，本文提出了基于可信区块链隐私计算平台的电子拍卖解决方案。

2 系统方案

2.1 算法模型

以下为基于可信区块链隐私计算平台方案需要使用的算法模型。

2.1.1 Paillier加法同态加密

Paillier提出了3种加密方案，其中的方案一具有良好的加法同态性：对多个密文执行乘法 运算，可以秘密实现明文加运算，即E(x+y) =E(x) ⋅E(y)[9]。同态加过程如下文所述。

对于密文c1和c2，乘积计算公式为c=c1⋅c2modn2，其中n为两个素数的乘积。

公钥(n,g)，私钥(λ,µ)生成步骤如下：

Step1 首先随机挑选大素数p和q，满足gcd(pq, (p− 1)(q− 1)) =1，并且满足p和q的长度相同。

Step2 计算n=pq以及λ=lcm(p− 1,q− 1)， 其中lcm为最小公倍数，为n的比特长度。

2.1.2 CKKS全同态加密

Cheon团队在2017年提出了基于CKKS的全同态加密方案，如图1所示，可以对浮点数进行近似计算，在多个全同态加密算法中效率较高[10]。其主要步骤为：

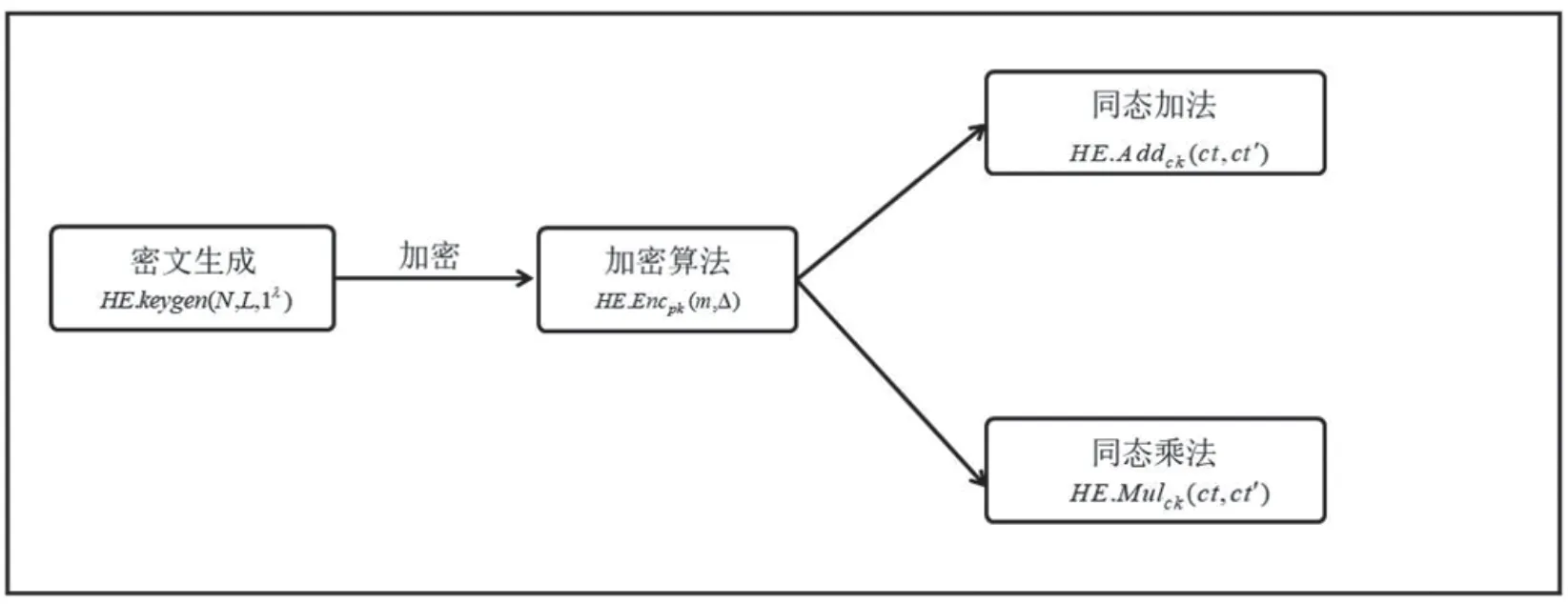
图1 CKKS全同态加密算法流程

Step1 密文生成算法HE.keygen(N,L,1λ)：其中N为多项式次数，λ为安全参数，L为层次参数，输出公钥pk、私钥sk和计算密钥ck。

Step2 加密算法HE.Encpk(m,∆)：其中m为需要加密的消息，输出密文ct。

Step3 同态加法HE.Addck(ct,ct′)：其 中ct和ct′分别为明文m和m′对应的密文，输出m+m′对应的密文。

Step4 同 态 乘 法HE.Mulck(ct,ct′)：其 中ct和ct′分别为明文m和m′对应的密文，输出m×m′对应的密文。

2.1.3 区块链

区块链是比特币的基础支撑技术，首次出现在中本聪（Satoshi Nakamoto）发表的《比特币：一种点对点式的电子现金系统》中[11]。区块链是一个共享的不可篡改的账本，采用分布式自治技术，具有不可篡改性、去中心化、可溯源性等特征。根据开放程度，区块链可划分为公有链和联盟链，任何人都可以自由加入公有链，而只有拥有特定权限的个人或组织才可以加入联盟链[12]。

2.1.4 智能合约

智能合约具有规范性、不可逆性、不可违约性、匿名性等特点。其中，规范性是指智能合约是以计算机代码为基础，通过严密逻辑结构来呈现内容，并且对合约上的所有计算机节点是透明的。不可逆性是指一旦完成约定的条件，合约就可以自动执行对应的预期计划。不可违约性是指在链上的信息公开透明，任何节点都可以追溯流程。匿名性是指在区块链上流程是透明的，但交易双方是匿名的。

2.1.5 Keccak256算法

Keccak256算法是一种加密散列算法，是第三代安全散列算法。在Keccak256算法被确定选为SHA-3标准的获胜算法后，就表现出很强的抗实际攻击的特性[13]，与SHA-1和SHA-2协议相比，SHA-3没有输入长度上的限制。

2.2 方案模型

基于同态加密和区块链技术的可信区块链隐私计算平台的电子拍卖模型如图2所示。该方案是针对当前电子拍卖隐私保护场景提出的一种隐私保护解决方案，有效保护了竞拍者、拍卖人的竞拍策略，竞拍金额等隐私问题，该方案包括以下实体：竞拍者、区块链、智能合约、消息认证、计算节点、拍卖机构、拍卖人。

图2 基于可信区块链隐私计算平台的电子拍卖模型

（1）竞拍者。竞拍者需要保护自己的拍卖金额、拍卖策略，同时对于拍卖流程要求透明化，对于最后拍卖成功的交易流程要求可溯化。

（2）区块链。采用联盟链的方式，竞拍者、拍卖人、拍卖机构均作为多方参与者进入联盟链共享信息，与传统公有链相比，联盟链的方式更加灵活、交易的成本更低、区块打包时间更少。

（3）智能合约。接受用户的拍卖金额同态加密密文以及竞拍金额的Hash值来上链，并打包成相应区块，同时提供区块链上的随机数生成函数。

（4）消息认证。通过对用户的个人信息、竞拍金额进行区块链Hash加盐签名，采用Keccak256算法来预防用户篡改金额以及在最终拍卖验证阶段完成交易。

（5）计算节点。通过在对应服务器上部署相应同态加密服务，对用户传输的密文进行操作。

（6）拍卖机构。拍卖机构同时对拍卖物品进行出价，应对电子拍卖过程中的流拍问题以及恶意出价问题。

（7）拍卖人。拍卖人对拍卖物品进行出价，作为拍卖物品的底价，并可以对低价进行保密处理，达到盲拍的效果。

2.3 方案模型

该设计方案大体可以分为委托者出价、拍卖机构出价、竞拍者竞价、交易完成4个阶段，如图3所示。

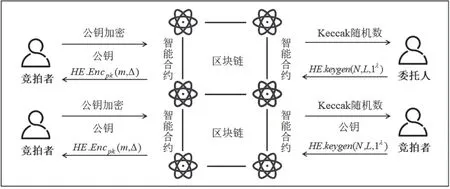
图3 基于同态加密单次比较算法流程

2.3.1 委托者出价

首先由委托者出价，委托者通过调用本文设计的算法3基于同态加密的隐私比较算法将自身的出价金额密文托管到平台，并调用智能合约将金额信息签名，并将签名值记录上链。

2.3.2 拍卖机构出价

拍卖机构为了防止线上平台委托者随意出价导致流拍率过高，需要对拍卖品价格进行预估，若起拍价高于预估价格3倍以上，则判定为恶意拍卖，若发生多次则禁止该藏品参与拍卖。

2.3.3 竞拍者竞价

在委托者出价以及拍卖机构验证之后，竞拍者就可以对藏品进行竞价，但基于个人隐私保护以及竞价策略保护的需要，竞拍者并不知道藏品当前竞拍价格以及其他竞争者出价，只能调用平台的隐私比较算法进行比对，得到的结果只是大小关系而不是真实的明文，若出价成功即当前的价格超过之前的其他竞拍者的价格或者为第一次出价超过委托者价格，则会更新为新价格密文，其中每次交易更新都会调用智能合约对相关信息作出签名并记录上链。同时为了防止竞拍者对价格进行爆破攻击，每个竞拍者对当前出价有且仅有3次机会。

2.3.4 交易完成

一旦新的价格密文在设定的时间内不变，就可以完成交易，若价格密文和起拍密文相同，则判定为流拍。交易完成后，需要将相应的交易过程上链，包括每次的价格密文以及竞拍者的相应Hash值，达到交易过程公开化，可追溯化。

2.4 算法设计

本文设计的智能合约基于Hyperledger Fabric架构，所涉及的变量和方法名如表1所示。

表1 智能合约的变量和方法名

合约主要分为3个主体函数，即随机数生成函数、存储函数、查询函数。随机数生成函数以区块打包的时间和难度作为种子调用Keccak256来生成随机数。存储函数采用Storage在链上永久存储，对传入的结构体存入至链上以供查询。查询函数则提供了查询接口，通过对应Hash值可以查询结构体。

使用的算法分别是基于同态加密的隐私比较算法、基于区块链的消息认证算法、基于区块链的随机数生成算法。3种算法的基本参数如表2所示。

表2 算法相关参数

续表

2.4.1 区块链随机数生成算法

区块链随机数生成算法使用联盟链上的当前区块难度和打包时间作为种子生成随机数，并多次重复Hash函数，即将上一次生成的随机数作为数据源重复进行Hash运算，提高攻击成本。

算法1：区块链随机数生成算法

2.4.2 区块链消息认证算法

使用者首先需要调用写入智能合约的区块链随机数生成算法生成随机数作为盐值参与运算，之后将盐值插入到传递信息的末尾作为预处理，调用Keccak256算法生成Hash值，通过盐值可以有效防止彩虹表攻击。

算法2：区块链消息认证算法

2.4.3 基于同态加密的隐私比较算法

首先起拍价的委托人调用算法1生成两个随机正整数（x和y），并对这两个正整数调用区块链消息认证算法获得Hash值上链，之后竞拍者调用Paillier算法生成一对公私钥，使用公钥加密价格并将公钥和加密密文发送给委托人，委托人调用智能合约将公钥和加密密文上链作为记录，并同时使用公钥计算出明文加密的结果E(b⋅x+y)，之后调用Paillier同态加密算法计算出E(a⋅x+y) =E(a)x⋅E(y)，其中a，b为随机正整数，将这两个结果调用智能合约上链记录。竞拍者得到计算结果后使用私钥解密出金额A=a⋅x+y和金额B=b⋅x+y，只需要比较A，B的大小就可以知道金额的大小。但此时委托人不知道金额的相对大小，因此需要交换一次顺序，重复一次上述流程来得到金额的相对大小，单次流程图如图3所示。两次流程结束后双方就可以确认对应的大小关系。

算法3：基于Paillier同态加密的隐私比较算法

3 安全性与可行性分析

通过第三节提出的方案，每个用户竞拍时都不会泄露自身具体金额，并且在整个竞拍环境下竞拍者不会泄露自身的竞价策略，而只是知道和藏品当前价格大小关系，为了防止用户使用穷举攻击，对每个价格出价时间和出价次数有着严格的限制。

对于交易过程中的竞拍者和委托者的不诚实问题，在每一次竞拍过程中都会做一次Hash记录上链，在拍卖结束之后，如果有竞拍者对过程有疑问，则可以重新签名认证金额。

算法1区块链随机数生成算法采用了从区块链上调用智能合约Keccak256散列算法并结合打包区块的难度和时间作为随机种子，多次Hash得到最终的随机数可以有效抵御碰撞攻击。

算法2区块链消息认证算法基于Keccak256算法，通过使用算法1生成的随机数作为盐值，可以防止彩虹表对签名值进行攻击，并支持对用户需要认证的信息进行签名存储。

算法3基于Paillier同态加密的隐私比较算法，为了防止比较者之间的不诚实行为，采用了签名值上链作为防范，借助Keccak256算法的抗弱碰撞性作为最后完成对金额及信息验证的保证。

本文通过选择联盟链方案，对加入联盟链的用户进行严格的身份认证，可以获得更好的隐私控制，减少被恶意攻击的可能性。

在最终验证的时候，拍卖成功者需要拿拍卖成功那次签名信息去完成最终交易，进行签名认证，这样可以有效避免篡改攻击。

在拍卖和交易的过程中采用签名数据上链的方式可以有效避免数据篡改，达到交易全过程可溯源、可验证的效果。

4 实验分析

4.1 实验环境

本文方案的实验环境为云服务器，采用的系统为CentOS7操作系统，配置为4核心CPU，16 GB内存，2 Mbit/s外网带宽，采用的性能测试框架为benchmark。

4.2 实验步骤

基本平台如图4所示，支持多种同态加密算法进行相关性能测试。

图4 可信区块链隐私计算平台

如图5所示，实验平台对两个随机操作数进行Paillier加密，得到对应密文，通过生成的密文就可以进行对应同态计算。

图5 基于区块链隐私计算平台的同态加密

4.3 Paillier同态加密算法测试

采用benchmark性能测试框架对Paillier半同态加密算法和CKKS全同态加密算法进行电子拍卖场景下的性能测试，对于随机数的同态加法、标量乘法、解密和加密过程作出1 000次运算并取对应平均值，结果如图6所示，该结果表明Paillier同态加密算法性能在2 048位密钥的情况下优于CKKS同态加密算法，可以满足多人在线竞拍的需要。

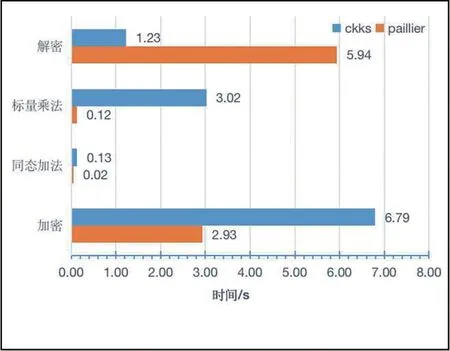
图6 CKKS和Paillier性能测试

5 结语

本文在电子拍卖的场景下，引入可信区块链隐私计算平台，针对拍卖过程中拍卖策略隐私保护的需要、拍卖金额隐私保护的需要、拍卖流程可溯的需要，提出了一种基于Paillier的半同态加密和区块链全程可溯源的隐私计算方案。

采用Paillier的半同态加密方案有效维护了多人电子竞拍策略以及金额隐私保护的需要，并在电子拍卖全流程中引入区块链，对整个流程进行信息上链，达到了拍卖流程可溯源、不可篡改的效果。

实验结果表明，与CKKS的全同态加密方案相比，基于Paillier的半同态加密的隐私计算效率可以更好地满足多人电子拍卖场景的需要，并实现拍卖流程中数据可用不可见的效果。