基于深度字典学习的滚动轴承故障识别*

余阿东

(信阳职业技术学院 汽车与机电工程学院,河南 信阳 464000)

0 引 言

滚动轴承经常在复杂环境中运行,易受各种外界干扰从而发生故障。在滚动轴承发生故障后,如何快速、准确地识别出故障类型及故障程度,对于提高故障定位精度和缩短整机恢复运行时间具有重要意义[1]。

目前,对滚动轴承故障进行诊断一般是基于振动信号进行[2],而实际采集到的振动信号常表现出非线性和非平稳性,导致传统的基于信号处理的故障识别方法受到较大限制[3]。

而基于深度学习的轴承故障识别方法无须构建复杂的滚动轴承物理模型。

丁家满等人[4]在对滚动轴承故障进行诊断时,采用重采样技术,提取了轴承振动信号的时域和频域特征,进而构建了深度森林模型,使滚动轴承故障的识别率达到了95%。王登峰等人[5]将深度Q网络引入了轴承的故障识别领域,建立了“博弈”诊断模型,建立了故障信号与不同故障程度之间的映射关系。

深度学习模型为一般黑箱模型。CHEN K等人[6]为解释故障机理,将轴承故障特征转换为灰度图;但是灰度图的物理含义不明确。

稀疏表示以字典原子的线性组合来重建信号,因此其所提取的字典原子与信号本身是线性关系,具有较重要的实际意义。

因此,笔者基于稀疏表示理论,借鉴深度学习“逐层提取特征”的思想,提出一种可用于滚动轴承故障识别的深度字典学习(DDL)模型;首先利用稀疏性约束逐层学习故障数据中的典型结构特征,然后构成深度故障字典,根据故障样本的重建误差确定故障类别,最后以滚动轴承试验台为对象测试DDL模型的有效性。

1 稀疏表示与字典学习

1.1 稀疏表示

稀疏表示是利用少量基本信号的线性组合来表示目标信号,其表达式如下:

y=Dx+v

(1)

式中:y—目标信号;D—字典;x—稀疏表示系数;v—误差。

字典D的每一列为一个原子,其单位化处理式如下:

(2)

由学习方法构造的字典是根据样本数据的特点自适应学习得到的,学习到的原子形态更丰富。因此,笔者使用学习方法来构造故障字典。

1.2 字典学习

在字典学习模型中,D和x为待求量,因此求解目标信号的稀疏表示可转换为:

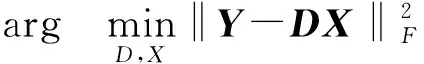
(3)

式中:Y—样本矩阵;X—稀疏系数矩阵;s—稀疏指标;‖·‖F—F—范数;‖·‖0—向量非零元个数。

笔者采用交替迭代法来求解式(3),其具体步骤是:

首先,固定D求解X;然后,固定X对D进行更新,重复上述操作,直到误差满足要求。

由字典D求解X是编码问题,此处笔者采用正交匹配追踪法(OMP)[7]进行求解。

此外,笔者采用SGK算法[8-10]进行字典D的更新,即:

(4)

(5)

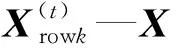
由于将学习到的字典应用于轴承故障识别时,不需要构建分类器,目标样本会由同属一类的字典原子稀疏表示出来,通过非零项系数的分布及重建误差,可将测试样本分配给对应类别。

2 基于DDL的轴承故障识别

2.1 样本矩阵生成

设样本数为M,样本维度为N。

滚动轴承故障类型如下:正常状态、内圈故障(轻微损伤尺寸0.18 mm,中度损伤尺寸0.36 mm,重度损伤尺寸0.54 mm)、外圈故障(轻微损伤尺寸0.18 mm,中度损伤尺寸0.36 mm,重度损伤尺寸0.54 mm)、滚动体故障(轻微损伤尺寸0.18 mm,中度损伤尺寸0.36 mm,重度损伤尺寸0.54 mm),共计10种工况类型。

其中,测试轴承的损伤尺寸由电火花刻蚀技术加工获得。

样本矩阵表示如下:

(6)

式中:Y∈N×M;Yi—第i(i=1,2,…,10)类样本的样本子集,Yi∈N×Mi;Mi—第i类的样本总数。

2.2 深度字典学习模型

笔者借鉴深度学习模型“逐层特征提取”算法,构建深层故障字典。每层字典的稀疏性指标设置为1,利用信号表示残差逐层驱动字典学习,其数学模型如下:

(7)

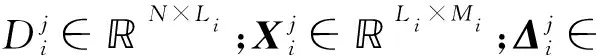
第j层字典Dj、系数矩阵Xj和残差矩阵Δj也按类别进行划分。残差矩阵Δj定义如下:

(8)

式(7)所示的约束优化问题可简化为无约束优化问题,即:

(9)

重复上述操作,直到字典层数等于设定的总层数n,所学习到的深度字典即可以用于故障识别。

DDL模型求解流程图如图1所示。

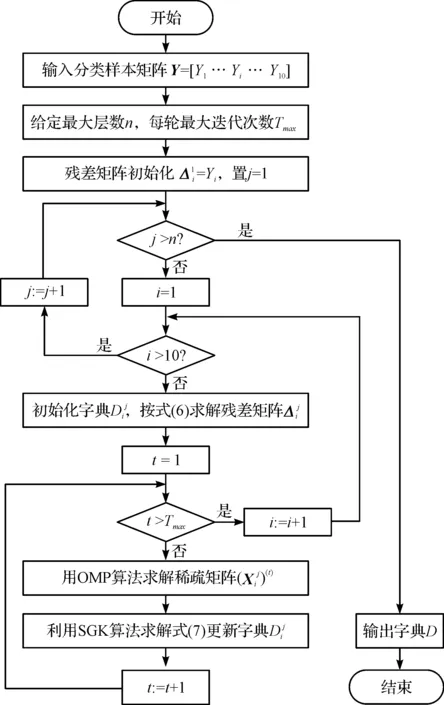
图1 DDL模型流程图

2.3 关键参数选择

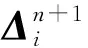
(10)

式(10)中,J越小误差越小,模型性能越好。

由于不同字典初值会影响迭代过程的收敛,从而最终会对模型性能造成影响。

K均值初始化、直接初始化和随机初始化3种不同初始化方法对模型的影响,如图2所示。

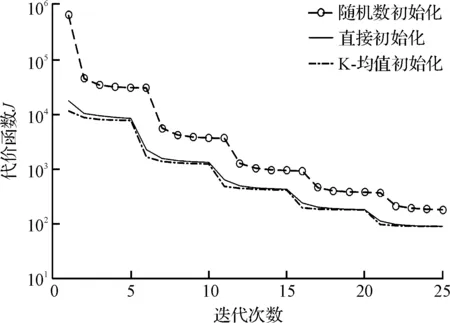
图2 不同初始化方法对模型性能的影响

由图2可知:K均值初始化方法效果最好,其内在结构上保证了初始化的字典中不会有特别相近的原子。因此,笔者选择K均值进行初始化。

字典的原子总数以及字典层数也是影响模型性能的重要因素。在理论上,增加字典规模和层数可使模型更精确,但同时也会增加字典学习过程中所需的时间和硬件资源。因此,此处应综合考虑模型性能和求解代价,选择合理的字典规模和层数,在保证模型性能的前提下,尽可能地缩短模型训练时间,并减少其对硬件资源的占用。

笔者对字典中原子总数占总样本总数的比例从0.1至0.5,字典层数从1层到8层的情况下,进行了迭代求解。

不同组合下,模型最终的代价函数取值如图3所示。

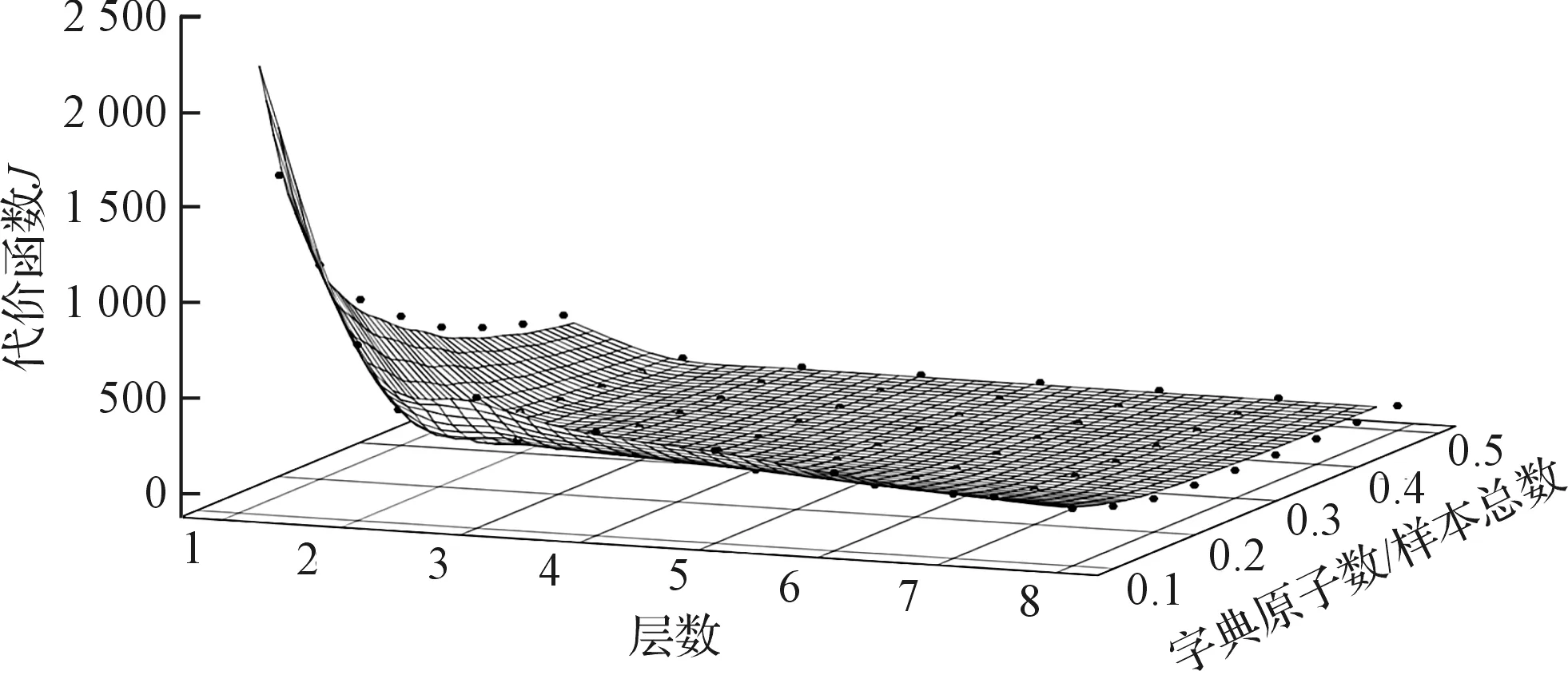
图3 字典规模及层数对模型性能的影响

由图3可以看出:当字典规模和层数增加到一定程度时,模型性能趋于稳定。此时,再增加字典规模和层数对模型性能的提升作用不大。

因此,笔者最终选定字典层数为5层,字典中原子总数占样本总数的比例为30%。

2.4 轴承故障识别

分类学习至各层字典后,笔者将同属一层的各类字典组成总子层字典,即:

(11)

对待识别的轴承故障样本y,在各子层字典Dj(j=1,2,…,n)上逐层求解稀疏表示系数,且各层的稀疏性指标均为1。由于此时字典Dj是已知的,只需利用OMP算法求解系数向量xj,然后利用残差更新公式逐层更新残差,最后进行信号重构。重构误差最小的类就是该样本所属故障类别。

具体判别方法如下:

(12)

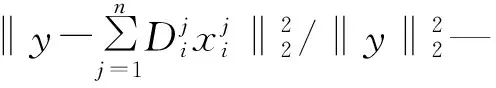
样本的深度稀疏表示如图4所示。

图4 样本的深度稀疏表示

3 实验验证

3.1 轴承数据

为验证深度字典学习DDL模型的有效性,笔者搭建了滚动轴承试验台,对故障轴承进行了测试。

滚动轴承试验台如图5所示。

图5 滚动轴承实验台

图5中的试验台由电机、转矩测量轴、滚动轴承测试模块、飞轮和负载电机等组成。

加速度传感器安装在试验台驱动端,轴承型号为6205-2RS JEM SKF;采样频率设置为12 000 Hz,转速为1 800 r/min;

此处,笔者设置4种工况状态:内圈故障工况、外圈故障工况、滚动体故障工况以及正常工况。

每种故障损失尺寸分别为0.18 mm、0.36 mm和0.54 mm。测试轴承的损伤尺寸是由电火花刻蚀技术加工得到的。

最后,实验所得数据集的每种工况包括3 000个训练样本、800个验证样本和1 000个测试样本。测试样本用于评估模型,每个样本包括1 024个采样点。

实验工况的设置如表1所示。

表1 实验工况设置

在10种工况下,滚动轴承的时域波形如图6所示。

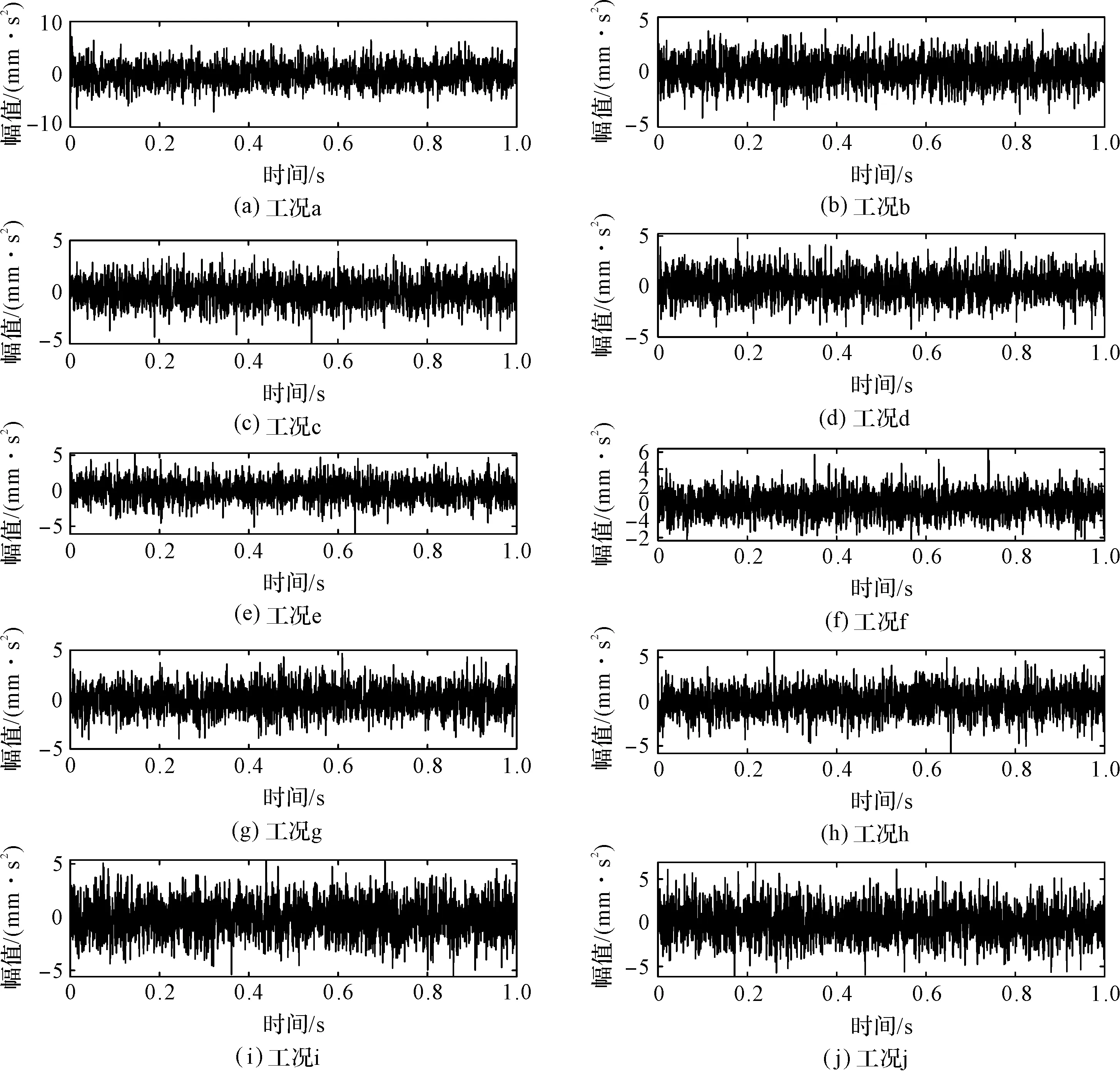
图6 时域波形图

10种工况下,滚动轴承相应的的包络谱如图7所示。

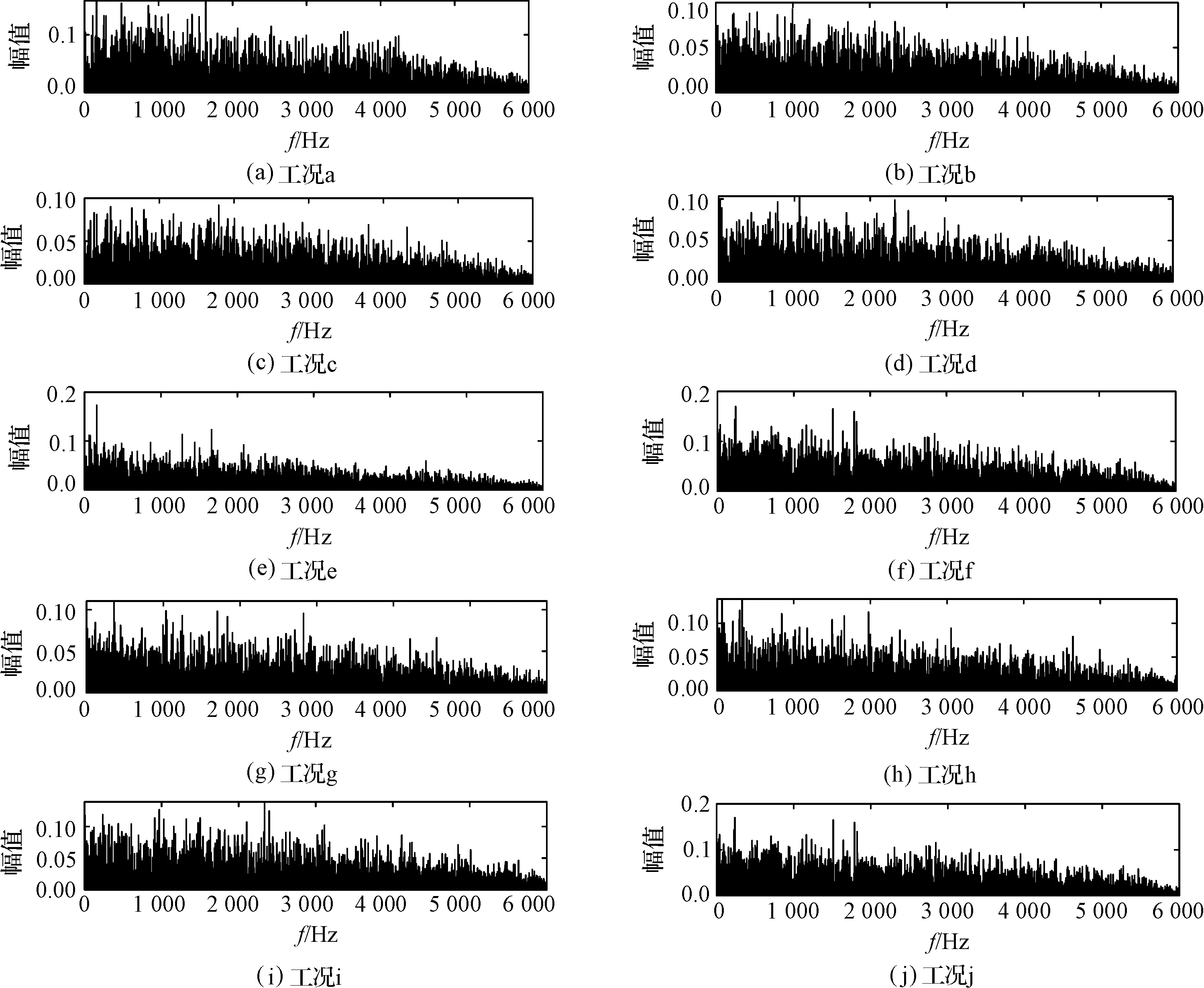
图7 包络谱图

由图(6,7)可知:滚动轴承的信号时域波形与包络谱图受噪声干扰严重,难以直接识别滚动轴承故障。

3.2 轴承故障识别与分析

在Winpython5.2.0环境下的Spyder编译器使用Python 3.8进行程序编写,深度学习框架为PyTorch 1.5。

其硬件以及软件环境如表2所示。

表2 程序运行环境

笔者将样本采用2.1节中的样本矩阵生成方法进行处理,得到样本矩阵;再利用深度字典学习模型求解方法迭代求解出深度故障字典D。其中模型关键参数的选择与2.3节中一致。后续故障样本的分类均基于该深度故障字典D实现,分类实现如2.4节所述。

为了测试深度字典学习DDL模型的性能,在相同数据集上,笔者使用文献[11]提出的CNN-LSTM深度神经网络(CNN-LSTM)、文献[12]提出的深度自编码网络(DSCN)、文献[13]提出的卷积神经网络和门控循环单元(C-GRU)进行对比分析。

在测试集上,不同模型的实验结果准确率取10次试验结果的平均值,如表3所示。

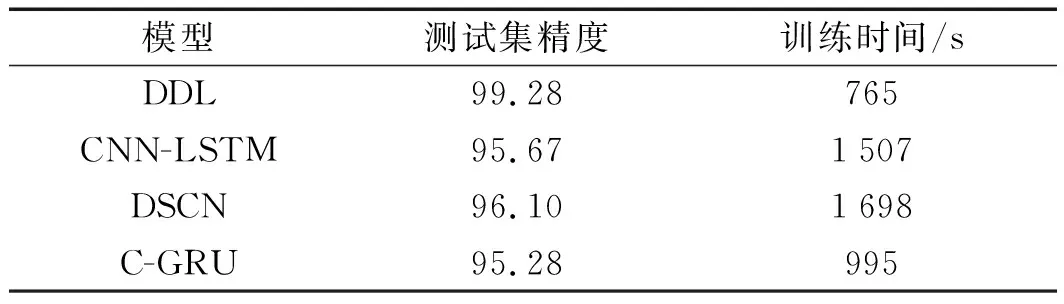
表3 不同模型的实验结果

由表3可知:

(1)采用DDL模型的滚动轴承故障识别准确率达到了99.28%,高于其他3种模型,且训练时间低于其他模型,这是因为数据驱动的字典学习方法能充分利用滚动轴承自身的海量故障数据提取故障特征;且训练算法非反向传播算法,梯度消失缺陷得以避免;

(2)在CNN-LSTM模型中,由于LSTM的梯度消失现象严重,识别准确率仅为94.67%,且LSTM的时间跨度较大,运算相对耗时;

(3)DSCN模型为全连接网络模型,所需要训练的参数众多,导致训练时间最长;

(4)C-GRU将CNN和GRU模型结合,GRU相对LSTM少一个门函数,因此,参数量少于LSTM,训练速度快于LSTM;但其识别准确率略低于LSTM。

基于DDL的诊断方法的第1次训练与测试过程Loss曲线,如图8所示。

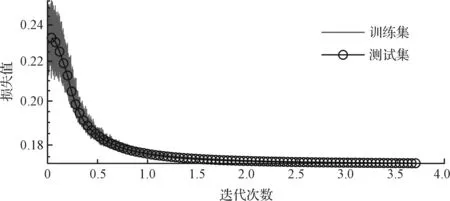
图8 Loss函数变化曲线

接下来,笔者进一步分析DDL模型的特征学习与故障识别能力。

基于DDL的诊断方法的第1次测试结果多分类混淆矩阵,如图9所示。

图9 第1次测试结果的多分类混淆矩阵

由图9可知:10种工况下,滚动轴承的故障识别准确率均达到了99%以上(工况f和g的识别准确率最高,达到了100%);正常工况下的识别率为99.17%,低于其他工况。

3.3 鲁棒性验证

考虑到实际运行环境中存在噪声,笔者对所提算法的抗噪性能进行验证,对采集到的故障样本添加高斯白噪声。

在不同噪声强度下,故障识别准确率和重建误差(样本实际所属类别字典的重建误差)的均值,如表4所示。

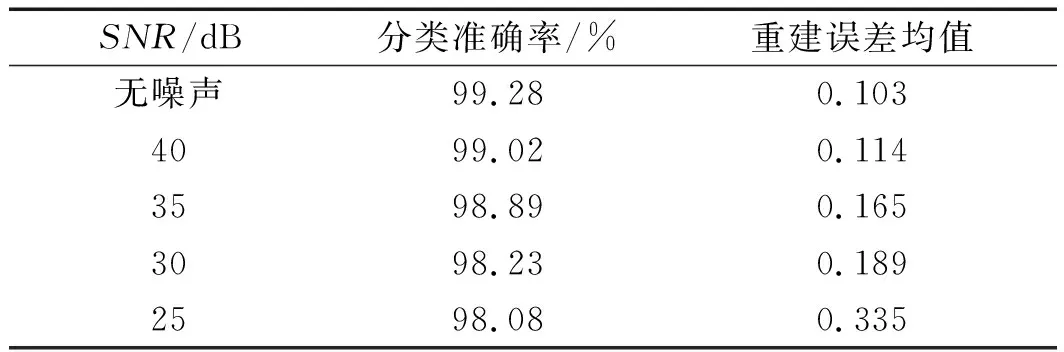
表4 抗噪性能验证

由表4可知:在不同噪声强度下,笔者所提出的DDL模型均可获得较高的故障识别准确率,且对样本的重建误差受噪声强度的影响较小。该结果证明了DDL模型具有较好的抗噪性能。

3.4 故障特征可视化

由于深度学习等基于数据驱动的特征学习算法的可解释性差,笔者构建了一个基于数据的特征学习模型,且所学习到的特征具有较好的物理含义。

外圈故障振动信号基于深度故障字典的稀疏表示结果,如图10所示。

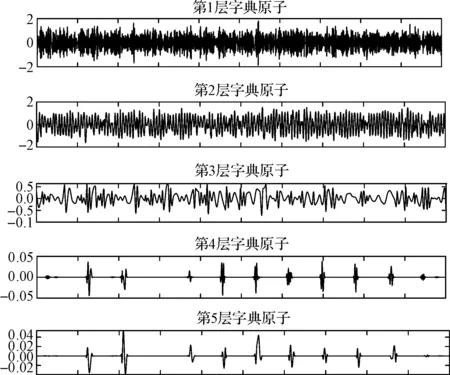
图10 稀疏表示字典原子

由图10可知:低层字典原子主要反映了故障样本的概貌特征,高层字典原子主要揭示了故障的细节特征(冲击特征),且随着字典层数的增加,突变量等细节信息更为凸显。

由此可见,这种从由概貌到细节的层次化特征提取方式,符合人们的认知过程,具有较好的物理意义[14,15]。

4 结束语

为了解决轴承故障识别算法存在的特征提取与选择困难的问题,笔者提出了一种基于DDL方法的滚动轴承故障识别方法,即利用字典学习的稀疏性约束逐层学习轴承故障数据中的典型结构特征,再根据故障样本结构构造了深度故障字典,根据样本的重建误差确定了其故障类别;实验结果表明,基于DDL的故障识别方法具有较好的识别效果。

主要研究结论如下:

(1)深度字典学习模型逐层自动提取故障特征,所提取的故障特征具有较好的物理含义;其中,低层字典包含了故障的总体特征,高层字典揭示了故障的细节特征,在一定程度上解决了故障特征的可解释性问题;

(2)基于数据驱动的字典学习方法,能充分利用滚动轴承自身的海量故障数据提取故障特征,用于解决如轴承系统复杂故障识别等物理建模过程过于复杂的问题。

笔者所设置的轴承故障缺陷是参考大多数文献所使用的电火花刻蚀技术得到的,与实际轴承缺陷的表现特征存在一定差别。因此,在后续的研究工作中,笔者拟将DDL模型方法应用于轴承全寿命周期故障信号,并进一步对DDL模型进行优化。