超启发式遗传算法柔性作业车间绿色调度问题研究*
2022-02-28屈新怀孟冠军丁必荣
屈新怀,纪 飞,孟冠军,丁必荣,王 娇
(合肥工业大学 机械工程学院,安徽 合肥 230009)
0 引 言
我国正处在由制造大国迈向制造强国的重要历史阶段,但是我国制造业整体资源消耗高,环境污染严重,产品却处于价值链的中低端。因此,转变制造业高消耗、高排放、低效率的粗放增长方式,促进制造业与生态环境协调发展,实现绿色制造是我国建设制造强国的必由之路[1]。
调度作为制造系统的重要环节,受到越来越多的重视,高效合理的绿色车间调度能够有效地实现节能减排、减少环境污染,较传统调度更符合当前的发展理念,更具应用价值。柔性作业车间调度问题(flexible job shop scheduling problem, FJSP)是作业车间调度问题(job shop scheduling problem, JSP)的扩展,释放了工序的资源约束,使问题更加贴近实际应用[2]。
近年来,越来越多的学者对绿色柔性作业车间调度问题进行了研究。刘琼等人[3]提出了产品制造过程碳足迹计算方法,建立了以碳足迹、完工时间、设备利用率为优化目标的多目标优化调度模型,设计了第二代非支配解遗传算法进行求解。雷德明等人[4]提出了一种基于新型优化机理的教学优化算法,以此来求解低碳柔性作业车间调度问题。李聪波等人[5]研究了考虑柔性作业车间广义能耗调度优化模型,基于模拟退火算法对模型进行了求解。李明等人[6]针对以完工时间、拖期、机器负荷和总能耗为目标的高维度多目标柔性作业车间调度问题,提出了一种新型帝国竞争算法对其进行了求解。MOKHTARI H等人[7]建立了以完工时间、设备利用率和总能耗为目标的多目标优化模型,提出了用遗传算法与模拟退火算法相结合的混合算法进行求解。LUO Shu等人[8]基于改进灰狼优化算法,求解了多目标柔性作业车间低碳调度。
上述文献都采用了启发式算法对柔性作业车间调度问题进行求解。启发式算法通常是根据特定的问题设置特定的搜索算子及参数,决定将哪种算子应用于特定的问题是一个持续的挑战。
但是,提前预测特定算子在特定问题上的表现是非常困难的;此外,调度环境和目标的变化会影响算法的求解能力,不能保证算法的求解效果。所以,在此基础上,通用性强的超启发式算法受到了越来越多学者的关注。
超启发式算法(HHA)是一种选择或生成启发式来解决计算搜索问题的搜索方法,致力于寻找一个好的方法来解决问题,是在一个启发式的搜索空间上操作,而不是直接在特定问题解决方案的搜索空间上进行操作;其由高层启发式策略(high level strategy,HLS)和低层启发式算子(low level heuristic,LLH)两部分构成,通过高层启发式策略选择或生成低层启发式算子来实现对解空间的搜索。
BURKE E K等人[9]提出了基于蚁群优化的遗传规划超启发式算法,求解混合流水车间调度问题,通过离线遗传规划生成了启发式调度规则,然后通过蚁群优化进行了选择。CHEN Lin等人[10]提出了一种基于粒子群算法的超启发式算法,求解车间调度问题。SU N等人[11,12]提出了超启发式交叉熵算法,求解模糊分布式流水绿色调度问题模型。
针对传统启发式算法通用性较差的问题,笔者建立多目标柔性作业车间绿色调度模型,设计超启发式遗传算法对问题进行求解;采用遗传算法作为高层启发式策略,并设计9种低层启发式算子;采用随机方法生成高层策略域种群,设计贪婪初始化方法生成低层问题域种群,最后通过标准算例及车间调度实例对算法性能进行验证。
1 柔性作业车间绿色调度问题
1.1 问题描述
柔性作业车间绿色调度问题可描述为:将n个工件安排到m台机器上进行加工,每个工件有多道工序且每道工序的加工顺序是确定的,每道工序有多台可选择加工机器,在不同加机器上的加工时间不同。
在加工过程中,机器有加工和空载两种状态,不同机器加工同一道工序产生的碳排放不同,机器空载状态也会产生碳排放。
柔性作业绿色调度问题是以能耗为目标,解决工序排序和机器选择两个子问题。工件完工时间为调度方案开始实施到工件最后一道工序完成加工所经历的时间,所有工件中完工时间最大的时间称为最大完工时间,最大完工时间是衡量车间生产性能的重要指标。
综上所述,笔者以最大完工时间和能耗为目标建立了柔性作业车间绿色调度模型。该问题满足以下假设条件:
(1)在初始时刻,机器和工件都处于可用状态;(2)工序加工过程不允许中断;(3)每台机器同一时刻只可加工一个工件;(4)不同工件相互独立,同工件的不同工序有加工顺序约束;(5)不考虑机器的准备时间和工件的搬运时间。
1.2 模型建立
此处优化目标是最大完工时间和能耗。笔者建立以最大完工时间和能耗为目标函数的数学模型如下:
f1=Cmax
(1)
(2)
i=1,2,…,n;j=1,2,…,Ni
(3)
Sij-Ci(j-1)≥0
i=1,2,…,n;j=2,3,…,Ni
(4)
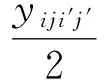
i,i′=1,2,…,n;j,j′=1,2,…,Ni;
k=1,2,…,m
(5)
i=1,2,…,n;j=1,2,…,Ni
(6)
xijk∈{0,1}
(7)
yiji′j′∈{-1,0,1}
(8)
式中:Cmax—最大完工时间;n—工件总数;Ni—工件i的工序数;m—机器总数;Oij—工件i的第j道工序;tijk—工序Oij在机器k上的加工时间;cijk—机器k加工工序Oij时,单位时间平均能耗;Sij—工序Oij的开始时间;Cij—工序Oij的完工时间;xijk—0-1变量,若工序Oij在机器k上加工为1,否则为0;yiji′j′—决策变量,若工序Oij为工序Oi′j′相邻的前一道工序则yiji′j′为-1,若工序Oi′j′为工序Oij相邻的后一道工序则yiji′j′为1,否则yiji′j′为0。
其中:式(1,2)为目标值;式(3)表示工序加工过程中不允许中断;式(4)表示同工件的不同工序加工顺序约束;式(5)表示每台机器同一时刻只可加工一个工件;式(6)表示每道工序只可被一台机器加工;式(7,8)均为决策变量。
最大完工时间和能耗两个评价指标的量纲和量纲单位不同,直接将目标值加权和作为目标函数,会影响求解的效果。为了消除其影响,笔者对目标值进行归一化处理;最后,对处理后同一量级的值进行加权和。
笔者采用min-max标准化对每个种群的目标值进行归一化,公式如下:
(9)
式中:min—种群中目标值f1的最小值;max—种群中目标值f1的最大值。
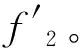
则目标函数如下:
(10)
其中:α1和α2分别为2个目标值权重系数,且满足α1+α2=1。笔者参考文献[13]142-143,取α1≈α2。
2 超启发式遗传算法设计
超启发式遗传算法是将遗传算法与超启发式算法相结合的一种算法。其高层启发式策略采用遗传算法,高层策略域个体的适应度值与对应问题域种群中最优解适应值相同,根据适应度值对高层策略域进行选择、交叉、变异操作。
笔者设计9种低层启发式算子,根据高层策略域个体的编码选择相应的算子,对问题域种群进行操作。
算法流程具体描述如下:
步骤(1)。初始化高层策略域种群和低层问题域种群;
步骤(2)。评价问题域种群;
步骤(3)。根据高层策略域染色体的适应度值对低层问题域种群依次进行低层启发操作,将更新后的解与原解进行比较,若更新后解的适应值优于旧解的适应值,用新解替换旧解;否则,按照一定概率接受新解;
步骤(4)。评价高层策略域种群,并对策略域种群进行选择、交叉和变异操作;
步骤(5)。对问题域种群进行选择;
步骤(6)。判断是否满足终止条件,满足则终止循环,输出最优解,否则转到步骤(2)。
2.1 高层策略设计
采用遗传算法作为高层启发式策略,在算法中,对低层启发式算子进行组合,获得高层策略域种群。在迭代过程中,新的个体通过对父代种群进行遗传操作来生成,用染色体中每个基因即低层启发式算子对问题进行求解。
每个基因在进行求解时,将更新后的解与原解进行比较,若更新后的解适应值优于旧解的适应值,用新解替换旧解;否则,按照一定概率接受新解,高层策略染色体的适应度值为新解的适应值。
2.2 低层算法设计
低层算子是由领域专家提供的,需根据实际问题进行设计。依据参考文献[14]概述的常用算子,笔者将低层启发式算子分为2类:交叉算子、变异算子;采用分段编码方式,染色体由工序排序染色体和机器选择染色体两部分构成,针对两部分分别设计低层算子(具体说明如下,用数字对工序进行编号,用“X”表示空工序)。
2.2.1 交叉算子
将各种交叉算子进行整合得到交叉算子示意图,如图1所示。

图1 交叉算子示意图
LLH1。顺序交叉(order crossover),在工序染色体上随机选择2个切割点,产生片段a和信息片段b,交换父代之间的信息片段,剔除父代1中与信息片段b冲突的基因,并将信息片段a中的基因从第二个交叉点开始从左向右依次插入,生成子代1;同理,对父代2进行操作;
LLH2。基于位置交叉(position-based crossover),随机生成一条与工序染色体长度相同的基因为0、1的染色体C,选取父代1、父代2,保留父代染色体与染色体C基因为1的位置相同的基因,得到染色体A、B,剔除父代2中与染色体A冲突的基因,将剩下的基因从左向右依次插入染色体A中得到子代1;同样,剔除父代1中与染色体B冲突的基因,将剩下的基因从左向右依次插入染色体B中,得到子代2;
LLH3。优先保持交叉(precedence preservative crossover),随机生成一条与工序染色体长度相同的基因为1、2的染色体C,从父代1(基因为1)到父代2(基因为2)中取未使用的最左边基因;
LLH4。多点交叉(multi-point crossover),该操作为随机生成一条与机器染色体长度相同的基因为0、1的染色体C,选取父代P1、P2,保留父代染色体与染色体C基因为1的位置相同的基因,交换父代与染色体C基因为0的位置相同的基因,得到两个子代染色体C1、C2;
LLH5。优先级操作交叉(precedence operation crossover),将工件分为工件集1和工件集2,选取父代P1和父代P2,将P1、P2中工件集1的基因分别复制到子代C1和子代C2中的相同位置,然后将P1、P2中工件集2的基因分别按P1、P2中的顺序依次填充到C2、C1中空余的基因位上,得到两个子代工序染色体C1、C2。
2.2.2 变异算子
LLH6。交换变异(swap mutation),在工序染色体上随机选择两个随机位置(p1,p2),并交换这些位置上的基因;
LLH7。移动变异(shift mutation),选择一个基因位置p,然后将位置p上的基因随机向左或向右移动s次;
LLH8。逆转变异(inversionmutation),在染色体中随机选择两个位置(p1,p2)之间的基因,将两个位置之间的基因逆序排列;
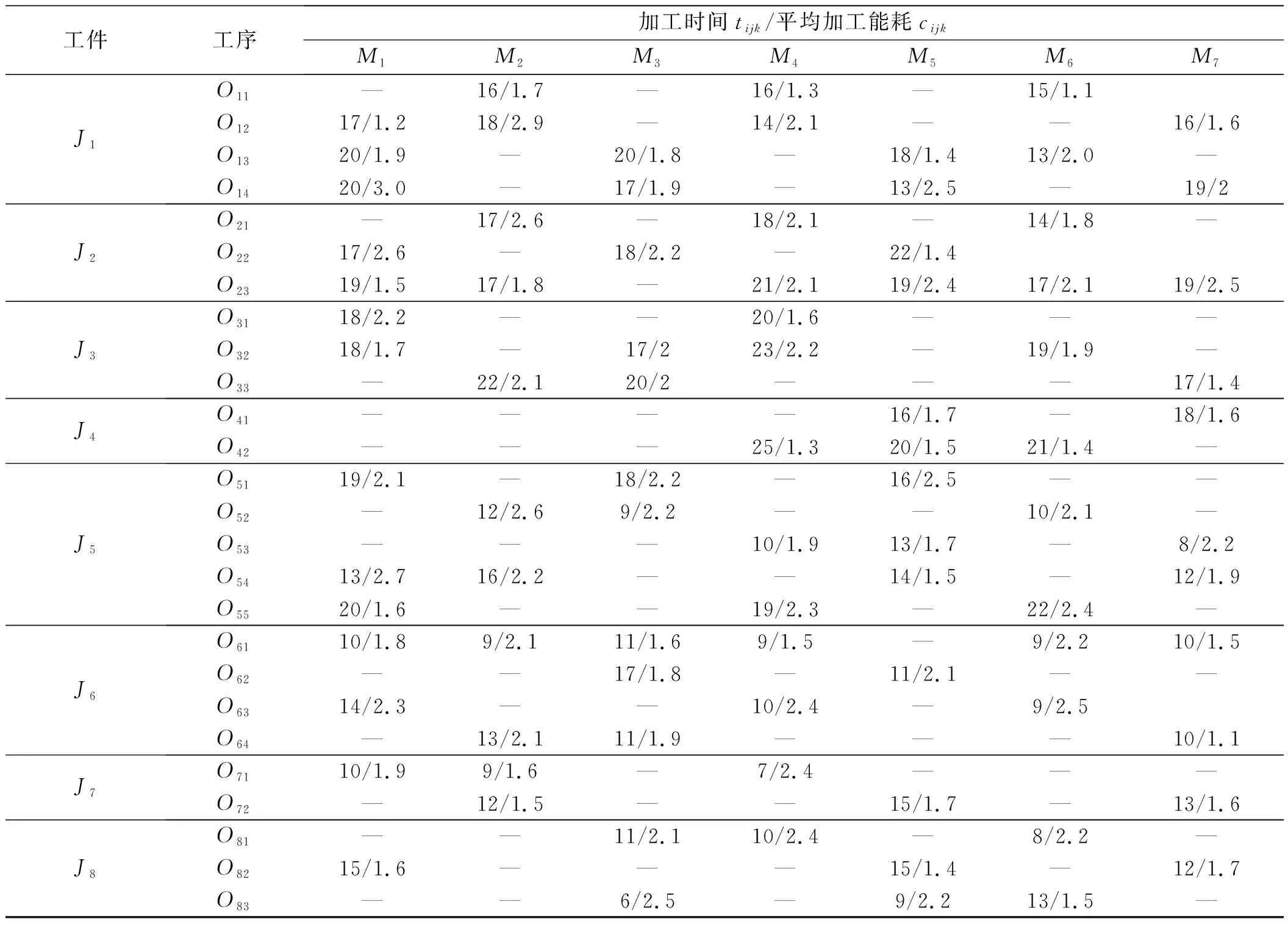
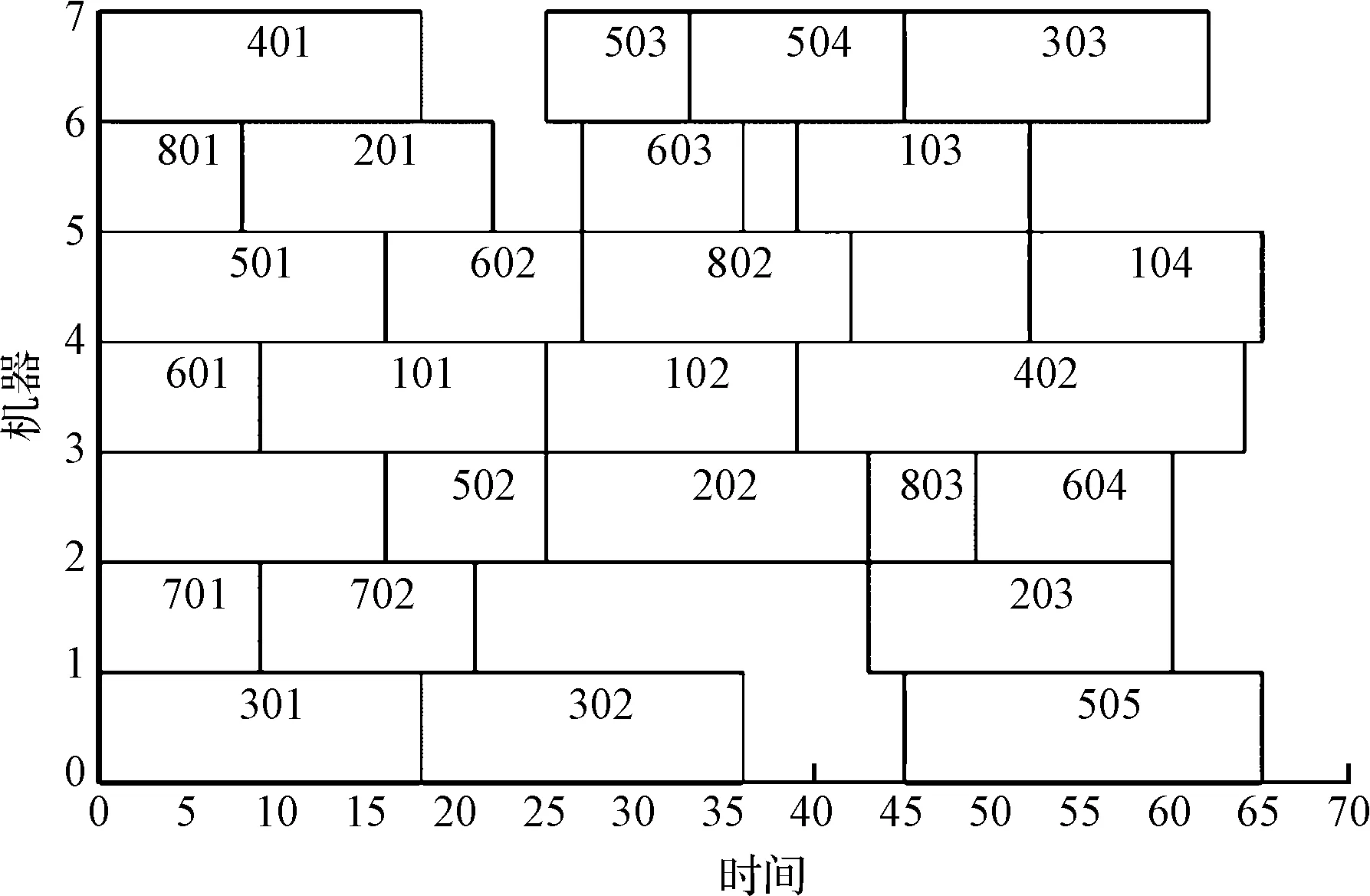
LLH9。随机变异(random mutation),选取父代P,随机生成一条与机器染色体长度l相同的染色体a,其基因为(0,1)之间实数,若a(i) 将各种变异算子整合得到交叉算子示意图,如图2所示。 图2 变异算子示意图 2.3.1 编码与解码 在高层策略域中,染色体中的每个基因是由上文的低层启发式算子构造,同一染色体中可以采用相同的低层启发式算子,染色体长度为6。 解码高层策略域染色体时,对低层策略域的种群,从左到右依次执行染色体中低层启发式算子,在执行完每个低层启发式算子后,对操作前后的两个解的适应度值进行比较,若更新后解的适应值优于旧解的适应值,用新解替换旧解,否则按一定概率接受新解,并继续执行余下的低层启发式算子。 高层策略域染色体示意图如图3所示。 图3 高层策略域染色体示意图 对低层问题域,采用分段编码方式,编码示意图如图4所示。 图4 问题域染色体编码 图4中:前段为工序排序染色体编码,用来确定工序加工顺序,数值i表示工件号,而数值出现的次数j表示该工件的第j道工序,对应的工序为Oij;后段为机器选择染色体编码,机器编码按顺序为工件J1,J2,…,Jn的工序选择的加工机器,用数值n表示选择该工序可加工机器集合中的第n台机器。 2.3.2 初始种群 采用随机初始化方法生成高层策略种群。 采用贪婪初始化方法对低层问题域种群进行初始化,具体流程如下: 步骤(1):设置参数。MPT:机器{M1,M2,…,Mm}对应的紧前工序完工时间,初始值为0;JPT:工件{J1,J2,…,Jn}对应的紧前工序完工时间,初始值为0;初始化基因位置参数k为1; 步骤(2):随机生成工序染色体编码OS; 步骤(3):为OS基因k上的工序Oij选择机器:根据可选择加工集Mij,对比MPT与JPT,确定工序Oij在可选择加工机器上的开始加工时间,加上加工时间以确定在每台机器上的完工时间,并计算在每台机器上的能耗,将完工时间及能耗进行归一化处理,选择加权和最小的机器加工工序Oij; 步骤(4):根据工序Oij选择的机器,更新MPT与JPT集合中的相应数据,k=k+1; 步骤(5):循环执行步骤(3)、步骤(4),根据OS为所有工序选择机器。 在Windows10操作系统中,笔者采用MATLAB R2016b编程语言,进行仿真实验。 笔者选取文献[15]基准算例,以最大完工时间Cmax为目标,验证基于贪婪初始化方法生成初始化种群的遗传算法运行效率,并与随机初始化的遗传算法和文献[16]146-149采用的改进初始化的遗传算法进行比较。 分别迭代200次后,收敛对比图如图5所示。 图5 迭代收敛对比图方法1为随机初始化遗传算法,方法2为文献[16]150采用的遗传算法,方法3为笔者采用贪婪初始化的遗传算法;从左至右依次为8×8、10×10、15×10问题 从图5可以看出:方法一和方法二迭代200次后陷入局部最优解,方法三可以快速跳出局部最优解,获得全局最优解。 可见,采用贪婪初始化生成初始种群的算法具有较快的收敛速度和较高的运行效率。 为验证超启发式遗传算法的有效性,笔者选取文献[13]143提出的算例(即一个简化后的8×7 FJSP方问题,表示车间内有8个工件,在7台机器上进行加工的车间调度问题),以最大完工时间和能耗为目标,对加工车间调度方案进行优化。 具体数据如表1所示。 表1 加工车间简化后的FJSP实例 笔者将采用超启发式遗传算法所得结果,与采用遗传算法[13]142-143和免疫遗传算法[17]169-170所得结果进行了比较。 采用超启发式遗传算法得到较优结果的调度甘特图,如图(6~8)所示。 图6 调度甘特图(Cmax=64,Emin=676.3) 图7 调度甘特图(Cmax=65,Emin=657.6) 图8 调度甘特图(Cmax=69,Emin=647) 采用3种算法对相同算例进行求解,所得结果如表2所示。 表2 算例结果对比 对比分析表2中的数据可以看出:采用3种算法获得的3组解中,Cmax这个目标值最小都为64;并且在相同Cmax目标值下,采用超启发式遗传算法所得的Emin目标值小于其他算法。 由此可以得出结论: 在Cmax目标值上,超启发式遗传算法与其余两种算法水平相近;在Emin目标值上,超启发式遗传算法则优于其余两种算法,从而验证了超启发式遗传算法的有效性和通用性。 笔者对柔性作业车间绿色目标值调度进行了研究,以最大完工时间和能耗为目标,对目标值进行归一化处理,以目标值加权和为目标函数;提出了一种超启发式遗传算法,以此来对高度问题进行求解,其中高层策略采用遗传算法,并设计了9种低层启发式算法;采用随机方法生成高层策略域种群,并设计贪婪初始化方法生成低层问题域种群;最后,通过Kacem算例及实例的仿真结果与其他算法进行了对比,对算法的正确性进行了验证。 研究结果表明: (1)与参考算法相比,采用贪婪初始化生成初始种群的超启发式遗传算法具有较快的收敛速度和较高的运行效率; (2)采用超启发式遗传算法获得的解的质量不低于部分传统启发式算法,说明超启发式算法具有一定通用性。 在后续研究中,笔者将考虑更多实际因素,增加求解的目标,以提高超启发式算法的实用性。
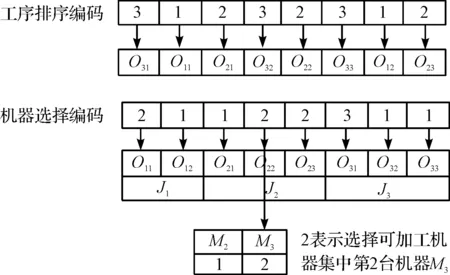
2.3 编码解码与初始种群

3 实例仿真与结果分析
3.1 算法性能分析

3.2 实例仿真分析



4 结束语
