极值点偏移问题在高考题中的应用及推广——以2021年新高考全国Ⅰ卷压轴题为例

广东省湛江一中培才学校 魏 欣 （邮编：524037）

2021年新高考全国Ⅰ卷压轴题中又出现了极值点偏移问题，追溯起来的话近十年高考压轴题中反复出现极值点偏移问题，分别在2010年天津卷、2011年辽宁卷、2013年湖南卷、2016年全国Ⅰ卷.而各地模考中此类问题更是层出不穷，作为压轴题自然综合性强、难度大，多数考生难以突破，在考试过程中会直接放弃，而要突破这一难题就要掌握解决此类问题的通性通法.何为通性通法？文[1]中章建跃先生认为：“通性”就是概念所反映的数学基本性质；“通法”就是概念所蕴含的思想方法.我们从极值点偏移问题说起.

1 极值点偏移问题的通性

1.1 极值点偏移问题产生的背景

当二次函数f（x）＝ax2+bx+c（a≠0）的图象与直线y＝m交于A（x1，m）、B（x2，m）两点时，线段AB的中垂线必过f（x）的极值点即当f（x1）＝f（x2）时，恒有则称极值点无偏移.因为二次函数的轴对称性，二次函数的极值点无偏移，但对多数给定区间内的单极值点函数f（x）而言，因在极值点两侧函数的“增减速率不同”，图象就不是轴对称的.即当f（x1）＝f（x2）时，常有则极值点发生偏移.

1.2 极值点偏移的定义

一般地，若连续函数f（x）在[a，b]有唯一的极值点x0，对于任意的x1、x2∈[a，b]，当f（x1）＝f（x2）时，有则称函数f（x）极值点偏移.

1.3 极值点偏移的类型及图示

图1

图2

图3

图4

1.4 极值点偏移问题在高考题中的设问形式及推广

高考题中出现最多的是形如“x1+x2＞2x0（或＜2x0）”的设问形式，比如2010年天津卷、2013年湖南卷、2016年全国Ⅰ卷以及2021年新高考全国Ⅰ卷；2011年辽宁卷中出现了形如“f′（）＞0（或＜0）”的设问形式，除以上设问形式外，还可将设问形式推广为证明：

2 极值点偏移问题的通法

极值点偏移问题是近年高考考查的热点问题，经过大量的研究应用，破解此类问题的技巧已经成为通法，下面举例进行阐述.

2.1 构造对称函数法

我们有这两点基本的认识：第一，如果函数f（x）满足f（x）＝f（2a-x），则f（x）图象关于直线x＝a自对称；第二，函数y＝f（x）与函数y＝f（2a-x）的图象关于直线x＝a互对称.这里要构造对称函数依据的是第二点.

要判断函数f（x）是否关于直线x＝a自对称，可以通过构造f（x）关于直线x＝a的对称函数f（2a-x），然后比较两函数在极值点同侧是否完全相同即可作出判断.基于此，可以得到极值点偏移问题最基本、最奏效的破解策略——构造对称函数法.

例1（2021年新高考Ⅰ卷22题节选）已知函数f（x）＝x（1-lnx），设a、b为两个不相等的正数，且blna-alnb＝a-b，证明e.

解析易知f（x）在 （0，1）内单调递增，在（1，+∞）内单调递减，故x＝1为f（x）的极值点.blna-alnb＝a-b可变形为不妨设且x1＜x2，易 知 0＜x1＜1＜x2＜ e，则f（x1）＝f（x2），下证 2 ＜x1+x2＜ e.

先 证x1+x2＞2.构 造 函 数g（x）＝f（2-x）＝（2-x）[1-ln（2-x）]，（x＜2）（如图5虚线所示），下面比较f（x）与g（x）在极值点左侧的大小，令h（x）＝f（x）-g（x），（0＜x＜1），h′（x）＝-lnx-ln （2-x），h′（x）＞ 0，故h（x）在 （0，1）内单调递增.则h（x）＜h（1）＝0，即当 0＜x＜1时 ，f（x）＜g（x）.因 为 0＜x1＜ 1，由f（x1）＜g（x1）得f（x2）＜f（2-x1），又x2＞ 1，2-x1＞ 1，函数f（x）在（1，+∞）内单调递减，故x2＞ 2-x1，即x1+x2＞ 2得证.

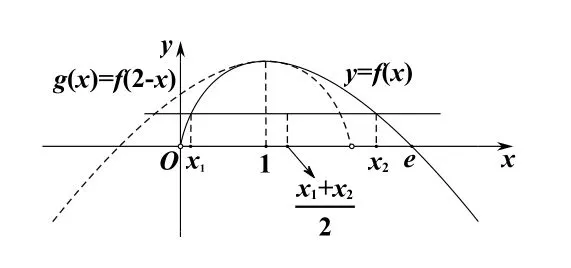
图5

再 证x1+x2＜e.构 造 函 数u（x）＝f（ex）＝（e-x）（1-ln （e-x）），（x＜ e）（如 图6 虚线所示），下面比较f（x）与u（x）在左侧的大 小 ，令m′（x）＝-ln （ex-x2），易知函数m′（x）在内单调递减.又由零点存在性定理，存在使得m′（x0）＝0，则m（x）在 （0，x0）内单调递增，在内单调递减，又故当时m（x）＞0，即f（x）＞u（x），因 为由f（x1）＞u（x1）得f（x2）＞f（ex1），又x2＞ 1，e-x1＞ 1，函数f（x）在（1，+∞）内单调递减，故x2＜e-x1，即x1+x2＜e得证.

图6

点评通过上例，可以归纳出构造对称函数法的具体解法步骤：

（1）求f（x）在[a，b]内的极值点x0；

（2）构造f（x）关于直线x＝x0的对称函数g（x）＝f（2x0-x）；

（3）比较直线x＝x0一侧f（x）与g（x）的大小（常作差比较，有时也可利用不等式直接比较），得 到 抽 象 不 等 式f（x）＜f（2x0-x）（或f（x）＞f（2x0-x））；

（4）利用f（x）在极值点一侧的单调性，去掉符号“f”，得到结论.

在极值点偏移问题中，构造对称函数解设问形式形如“x1+x2＞ 2x（0或 ＜ 2x0）”的题目时非常有效，它的实质是利用原函数的单调性解抽象不等式，所以对原函数做到“心中有图”，是顺利解题的不二法宝.需要注意的是，通过高考题及模考题的广泛运用，这种技巧已经被固化成了一种通法，要明确构造的目标是解抽象不等式，所以当题目出现形如“x1x2＞x2（0或 ＜x20）”的设问形式，也就不难想到应该构造函数类比以上解法破解题目.

类题演练（2016年高考全国Ⅰ卷21题节选）已知函数f（x）＝（x-2）ex+a（x-1）2有两个零点x1、x2.证明：x1+x2＜ 2.

2.2 比值换元法

对于含对数式的极值点偏移问题，可以考虑依据已知条件f（x1）＝f（x2）列方程组，尤其当原函数中含有参数时，通过两方程作差或求和可消去参数，将问题转化为只含x1，x2的双变量问题，再利用比值换元（即），构造关于t的函数解题.

例2（2011年高考辽宁卷21题节选）已知函数f（x）＝lnx-ax2+（2-a）x，若函数f（x）的图象与x轴交于A、B两点，线段AB中点的横坐标为x0，证明：f′（x0）＜ 0.

解析不妨设A、B两点横坐标分别为x1，x2，且x1＜x2，则要证f′（x0）＜ 0，即证2ax+2-a，故只需证a（x1+x2）+2-a＜0，因 为f（x1）＝f（x2）＝0，所以两 式 相 减 得故所以需证即证只 需 证g（t）＞ 0，因 为故g（t）在（1，+∞）内单调递增，即g（t）＞g（1）＝0.

类题演练已知函数f（x）＝lnx-ax，若x1、x2是函数的两个零点，且x1＜x2，证明：x1x2＞e2.

2.3 差值换元法

对于含指数式的极值点偏移问题，可以考虑依据已知条件f（x1）＝f（x2）列方程组，与比值换元法相仿，将问题转化为只含x1，x2的双变量问题，再利用差值换元（即t＝x2-x1），构造关于t的函数解题.

例3（2019年武汉调研22题节选）已知函数f（x）＝x-aex+1（a∈R ）有两个零点x1、x2，且x＜x，证明：ex1+ex2＞2.

12

解析由题意可得两式相减得两式相加得x2+x1+2＝只需证即证x1+x2＞ 0，令t＝x2-x1（t＞0），即 证即 证 （t-2）et+t+2 ＞ 0，构造函数g（t）＝（t-2）et+t+2（t＞ 0），g′（t）＝（t-1）et+1，g′′（t）＝tet＞ 0，故g′（t）在（0，+∞）内单调递增.g′（t）＞g′（0）＝0，即g（t）在 （0，+∞）内单调递增，g（t）＞g（0）＝0，ex1+得证.

点评上述两种解法如出一辙，都是利用题设条件列出方程组，通过对两方程作差或求和，得到含参数及x1、x2的方程，利用该方程消参得到只含x1、x2的不等式，消参规避了对参数的分析，简化了问题，同时从结论入手，结合分析法证明.而最后利用比值或差值进行换元，其实是一种常见的减元思想，通过换元将双变量问题成功转化为单变量问题，进一步简化了问题.此解法没有分析原函数的图象与性质，而是另辟蹊径构造了关于参数t的函数进行分析.这两种解法的亮点是将双变量x1、x2转化为单变量t，但同时也存在一定的局限性，有些题目是无法顺利转化的.

类题演练已知函数f（x）＝ex-ax+3a（a∈ R），其图象与x轴交于A（x1，0），B（x2，0）两点，且x1＜x2，证明

2.4 对数平均值不等式法

L（a，b）＝称为两个正数a、b的对数平均值（取等条件a＝b）称为对数平均值不等式.一些原函数中含有lnx或ex的极值点偏移问题，可以通过取自然对数等变形化为对数平均不等式模型加以证明.

例4已知有两个不等实根x1、x2，求证：

解析令0），则g（t）＝a有 两 个 不 等 实 根t1、t2，（不 妨 设内单调递增，在内单调递减，g（t）max＝方程g（t）＝a有两个不等实根，则由g（t1）＝a，g（t2）＝a，得

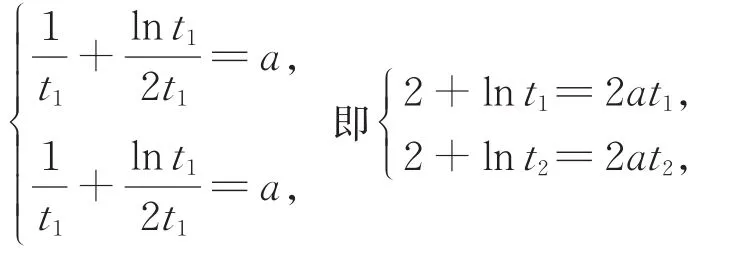
两 式 相 减 得 ：lnt1-lnt2＝2a（t1-t2），故（化为对数平均值不等式模型），其余步骤同例2.

点评通过适当变形将原问题化为对数平均值不等式模型，将不同的问题化归为同一类型，这样缩短了思维路径，解题过程充分展现了转化与化归的数学思想.

类题演练（2010年高考天津卷21题节选）已 知 函 数f（x）＝xe-x，如 果x1≠x2且f（x1）＝f（x2），证明：x1+x2＞ 2.

3 极值点偏移问题的演变与延伸

通过演变延伸，在模考试题中已经出现了单调函数拐点偏移的身影，那么什么是拐点偏移？

3.1 拐点的定义

设曲线y＝f（x）在点 （x0，f（x0））处有穿过曲线的切线，且在该点近旁，曲线在切线的两侧分别是严格凸和严格凹的，则该点为曲线y＝f（x）的拐点，其必要条件为f′′（x0）＝0.

3.2 拐点偏移产生的背景

极值点偏移与函数图象的轴对称性相关，而拐点偏移与函数图象的中心对称性相关，比如三次函数图象具有中心对称性，其对称中心恰是拐点，我们就称三次函数拐点不偏移.当函数（本文只针对单调函数）拐点不是其对称中心，即拐点两侧函数的“凸凹程度”不同，函数的拐点就会发生偏移.

3.3 拐点偏移的定义

一般地，若连续函数f（x）在[a，b]上有唯一的 拐 点x0，对 于 任 意 的 两 个x1、x2∈[a，b]，当则称函数f（x）的拐点偏移.当时，拐点x0在[a，b]内向左偏移（如图7）；当时，拐点x0在[a，b]内向右偏移.

图7

3.4 拐点偏移问题示例

例5（2019年深圳市一模改编）已知函数其定义域为（0，+∞），若函 数f（x）为 定 义 域 上 的 增 函 数 ，且f（x1）+f（x2）＝-4e，证明x1+x2≥ 2.

分析可求得（1，-2e）为函数的拐点，由题设f（x1）+f（x2）＝-4e知该题是拐点偏移的判断问题.文[2]给出了拐点偏移的判定方法，但对未学习高等数学知识的高中生而言，站位高，可操作性尚欠缺.既然极值点偏移问题可以构造对称函数破解，而作为极值点偏移问题的延伸，拐点偏移是否也可以通过构造对称函数破解呢？

极值点偏移是构造原函数关于直线的对称函数，究其原因是极值点偏移与函数的轴对称性相关，而拐点偏移与函数的中心对称性相关，不妨构造原函数关于拐点的对称函数一试.

解 析易知当a＝1时，f（x）为定义域上的增函数，故f（x）＝由f″（x）＝0，得x＝1，知f（x）的拐点为 （1，-2e），构造f（x）关 于 拐 点 的 对 称 函 数h（x）＝-4e-f（2-x）（x∈（0，2））（如图8虚线所示）.

图8

欲 证x1+x2≥2，需 证x2≥2-x1，即 证f（x2）≥f（2-x1），由f（x1）+f（x2）＝-4e，即证-4e-f（x1）≥f（2-x1），即证-4e-f（2-x1）≥f（x1），即证h（x1）≥f（x1）在 （0，2）内恒成立.即证即证

由基本不等式可知

类题演练设函数证明 ：当x1≠x2，且f（x1）+f（x2）＝-1 时 ，x1+x2＞2.