巧设问题情境 妙解压轴难题

福建省莆田第四中学 祁君华 （邮编：351100）

《普通高中数学课程标准解读》（2017年版，2020年修订）的前言指出：“基于核心素养的教学，要特别重视情境的创设和问题的提出”“设计情境和提出问题的根基是数学内容的本质”，由此可见，在日常教学中，设计合适的情境、提出合适的问题对于启发学生积极思考、感悟和形成数学核心素养的重要性.情境包括现实情境、数学情境与科学情境.新课的讲授一般都密切联系生活实际，设置现实问题情境或科学问题情境，进而引入相关的数学概念，如以“B景区游客人次的年增加量越来越大（非线性）”与“生物体内碳14含量与死亡年数之间的关系”引出“指数函数”的概念（数学必修第一册，2020年人教A版）.但高三的复习课与试卷讲评课显然与此有很大的不同，又要如何设置合适的问题情境，激发学生的兴趣，启发学生的思维，进而提高课堂教学效率呢？结合近期的高三复习教学实践，提出两点做法，和各位同行一起交流.

1 巧设阶梯问题情境，由浅入深，化繁为简

“标准解读”的前言进一步指出：情境与问题应该是多样的，多层次的.高三的一些综合性难题的讲解不能单刀直入，就题论题，让很多学生如坠云里雾中，或者是只知其然而不知其所以然.而是要通过巧设阶梯问题情境，步步为营，层层递进，让更多的学生积极参与思考、讨论.看似“踏破铁鞋无觅处”，实则“得来全不费工夫”.

例1已知函数不等式f（a·ex）+f（1-2x）≤1对∀x∈R恒成立，则实数a的取值范围是（ ）

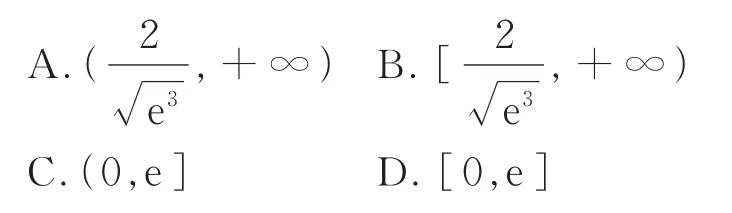
这道周练中的单选压轴题让大多数学生望而却步，得分率非常低.在讲评题目时，没有直接把关键的结论强塞给学生，而是通过巧设阶梯问题情境，不断地启发、引导学生自己去思考、讨论、探索.问题串如下（投影）：

问题1 讨论函数的单调性与奇偶性.

问题 2若f（x）满足f（-x）+f（x）＝0，则f（x）的图象关于原点对称.若f（x）满足f（a+x）+f（b-x）＝0，则f（x）图象的对称中心又是什么呢？

问题 3一般 地 ，若f（x）满 足f（a+x）+f（b-x）＝c，则f（x）图象的对称中心是什么？

问题4函数的图象有无对称中心？为什么？

问题5你能否利用“问题4”的结论化简不等式f（a·ex）+f（1-2x）≤ 1？

问题6求参数范围的最常用方法是什么？你是否已云开雾散，驶近胜利的彼岸？

其实“第1问”很简单，而“第2问”与“第3问”我在上一周已归纳总结过，只要能突破关键的“第4问”，接下来的一切都是水到渠成的.随着越来越多的“眉锁”被解开了，提问了两位情绪高涨的学生，然后在大家的齐声回答中，板书总结如下：

由已知可得f（a·ex）≤ 1-f（1-2x），从而f（a·ex）≤f（2x-1）.

因为f（x）为减函数，所以a·ex≥2x-1，即恒成立.

我来了个“急刹车”，突然转身问道：“有谁愿意帮我继续写下去？”

很快就有一位学生自告奋勇地走了上来，板演大致如下：

如此由浅入深，又深入浅出，不仅降低了题目的难度，活跃了课堂的气氛，让学生了解了相关知识与方法的来龙去脉，而且能让更多的学生体验成功，收获自信，何乐而不为呢？

2 巧设关联问题情境，由此及彼，一举突破

“标准解读”的前言还提到：三种情境的每种情境又可以分为熟悉的情境、关联的情境与综合的情境.当教师遇到评析一些构思新颖、难度较大的题目时，不宜操之过急，直奔主题，而是应该多设置一些关联的问题情境，这样做不仅能揭穿题目的“伪装”，看破真相，更能教会学生学会触类旁通，举一反三，感悟数学基本思想，发展学科核心素养.

例2数学王子高斯是德国著名的数学家，近代数学的奠基者之一，他和阿基米德、牛顿并列为世界三大数学家，用其名字命名的“高斯函数”为：设x∈R，用[x]表示不超过x的最大整数，则称y＝[x]为高斯函数，例如：[-3.5]＝-4，[2.1]＝2.已知函数f（x）＝sin[cosx]+cos[sinx]，关于f（x）有下述四个结论，其中正确的是（ ）

A.f（x）的一个周期是2π

B.f（x）是非奇非偶函数

C.f（x）在（0，π）单调递减

D.f（x）的最大值大于 2

这道月考试卷中的多选压轴题也让很多学生望而生畏，手足无措.在解析这道题目时，也没有选择正面迎击，而是通过巧设关联的问题情境，带领学生不断地旁敲侧击，待时机成熟了，再一举攻破“堡垒”.问题串如下（投影）：

问题1讨论“高斯函数”y＝[x]的图象与性质.

问题2作出函数y＝x-[x]的图象，并讨论它的性质.

问题3函数y＝x+[x]的图象与性质与y＝x-[x]的有何不同？

问题4以上三个函数是否有共同点？如果有，你能否据此猜想函数f（x）的某个特性并加以证明吗？

问题5与“高斯函数”相关的函数的图象都有何明显特征？请大家相互交流，并据此分析函数f（x）的单调性.离终点不远了，你是否已经看到胜利女神的微笑了？

授人以鱼，不如授人以渔.以下是几位学生的发言与板演：

由图可知（图1），高斯函数的值域为Z，它既没有单调性，也没有奇偶性与周期性.

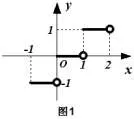
图1

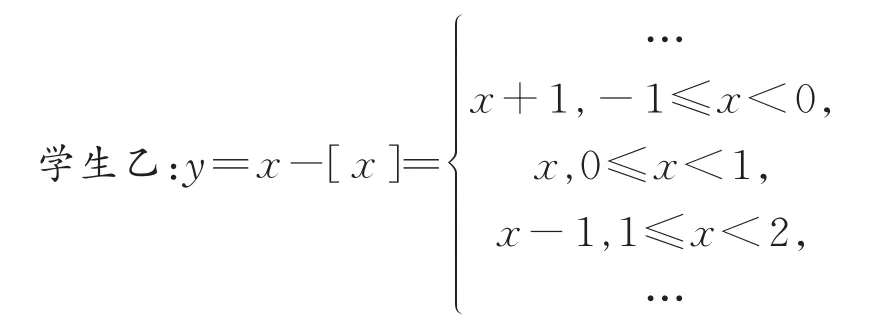
由图可得（图2），它的值域为[0，1），最小正周期为 1，单调增区间为 [k，k+1）（k∈Z），但没有奇偶性.

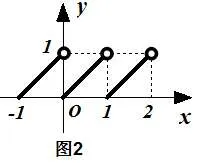
图2

学生丙：我发现这两个函数的性质迵然不同.数形结合可得（图3），函数的值域为[2k，2k+1）（k∈Z），它竟然是一个增函数，但没有奇偶性与周期性.

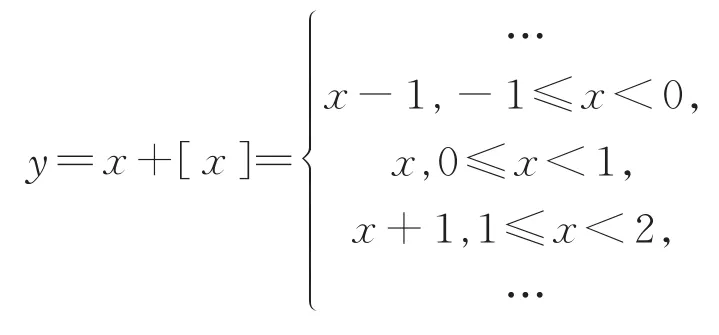
图3

尽量把这些问题分配给不同的小组，让更多的学生有展示的机会.

学生丁：三个函数的共同点是“都没有奇偶性”，由此猜想f（x）也没有奇偶性，可以举反例证明如下：

因为f（0 ）＝sin[1]+cos[0]＝sin1+cos0＝sin1+1≠0，所以f（x）不是奇函数.

又因为f（-1）＝sin[cos（-1）]+cos[sin （-1）]＝sin[0]+cos[-1]＝cos1，

f（1）＝sin[cos1]+cos[sin1]＝sin[0]+cos[0]＝1，

所以f（-1）≠f（1），所以f（x）不是偶函数.

教室里立即响起了一片热烈的掌声，我也频频点头称赞.随后我又补充了一句：“因为与高斯函数相关的函数的图象都呈左（端点）闭右（端点）开的分段式结构，所以这样的函数的图象一般都不具有对称性.当然，也不排除像y＝[cosx]与y＝sin[cosx]这样特殊的偶函数.好了，就剩最后一个问题了，谁来替我画上一个完美的句号？”话音未落，就有一位学生抢先站了起来.

学生戊：其实很简单，只需判断f（x）在区间上的单调性即可.

大功告成！通过解一题，让学生通一法，会一类.如此这般讲题、解题，岂不快哉？

3 结束语

总而言之，教师在评析练习与试卷中的一些较难的题目时，若能多设置一些阶梯问题情境与关联问题情境，不仅能深入浅出，化繁为简，出奇制胜，更能启发学生独立思考，鼓励学生相互交流，让他们充分领略数学解题之美，理解数学的本质，进而有效发展数学学科核心素养.