提升归纳推理素养 启迪学生思维之光

浙江省新昌中学 张 淦 （邮编：312500）

日常教学中，“下笔难”“想不到”“没思路”是学生求解数学问题时的常有现象.特别是面对“新”题目，学生常常感叹“寻寻觅觅，冷冷清清，凄凄惨惨戚戚”.作为教师，如何启迪学生思维之光，探寻“破题”关键，是教学的现实需要.

归纳推理作为逻辑推理的方式之一，具有启迪思路、发现知识的功能.从具体到抽象，从简单到复杂、从特殊到一般，从猜想到证明是基本的归纳推理策略.

1 “具体”入手，“抽象”落地

例1（2020.浙江卷第10题）设集合S、T，S⊆N*，T⊆N*，S、T中至少有两个元素，且S、T满足：

①对于任意x、y∈S，若x≠y，都有xy∈T

②对于任意x、y∈T，若x＜y，则下列命题正确的是

A.若S有4个元素，则S∪T有7个元素

B.若S有4个元素，则S∪T有6个元素

C.若S有3个元素，则S∪T有5个元素

D.若S有3个元素，则S∪T有4个元素

解 析当S＝{1，2，4} 时 ，T＝{2，4，8}，S∪T＝{1 ，2，4，8 }排除 C;

当S＝{2，4，8}时，T＝{8，16，32}，S∪T＝{2，4，8，16，32 }排除 D;

若取S＝{ 2 ，4，8，16 }，则T＝{ 8 ，16，32，64，128 }，此时S∪T＝{2 ，4，8，16，32，64，128 }，包含 7个元素，选A.下证选项A是正确的.

设 集 合S＝{a，b，c，d}，且a＜b＜c＜d，a、b、c、d∈N*.由条件①可得:ab、ac、ad、bc、bd、cd∈T，再由条件②可得{a，b，c，d}.注意到都成立，得到b＝a2，c＝a3，d＝a4，且a≠1，所 以S＝{a，a2，a3，a4}，T＝{a3，a4，a5，a6，a7}，得到S∪T＝{a，a2，a3，a4，a5，a6，a7}.

反思此题以集合与元素为背景，符号多、抽象性强、问题的本质学生难以识别.我们通过具体实例，推理得到问题的本质是元素的互异性和唯一性.

2 “简单”开始，力克“复杂”

例2（2021.绍兴市期末统考卷第10题）已知递增数列{an}的前 100项和为 Sn，且a1＞ 0，a100＝2，若当 1≤i＜j≤ 100时，ai-aj仍是数列{an}中的项（其中n、i、j∈N*），则

解析为了降低思维的起点和难度，我们不妨采用归纳推理的处理办法，不妨遵循从简单到复杂、数据从小到大的归纳推理策略.

令i＝1，j＝2，则a2-a1∈{a1，a2，…，a100}，因为a2-a1＜a2，所以a2-a1＝a1，得到a2＝2a1.

事实上，人教版数学必修5等差数列第一课时，设置了如下的数列场景.

（1）我们经常这样数数，从0开始，每隔5数一次，可以得到数列：

0，5，___，____，____，….

（2）水库每天的水位组成数列（单位:m）18，15.5，13，10.5，8，5.5.

（3）存款各年末的本利和（单位:元）组成数列：10072，10144，10216，10288，10360.

材中这样的编写安排，从特殊到一般，起点低，契合学生的认知规律.“从特殊入手，研究数学对象的性质，再逐步扩展到一般，这是数学常用的研究方法[1]”.

3 “特殊”顺利，“一般”成章

例3（2014年1月浙江省普通高中学业水平测试第25题）如图，在 Rt△ABC中 ，AC＝1，BC＝x，D是斜边AB的中点，将△BCD沿直线CD翻折，若在翻折过程中存在某个位置，使得CB⊥AD，则x的取值范围是（ ）

解析若存在某个位置，使得CB⊥AD，只需过点C作直线AB的垂直平面α，若满足B∈α，则有CB⊥AD.遵循特殊到一般的推理分析策略，考虑三种特殊的情形.

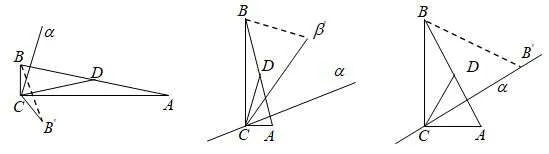
当x→ 0，即时，翻折终止时，点B关于直线CD的对称点B′和点B位于平面α异侧，因此翻折过程中存在某个位置，使得B∈α，因此x→0可以；

当x→+∞，即时，始终有B∉α，因此x→+∞不可以.

当翻折终止，恰好有B′∈α时，则有∠DBC＝∠BCD＝∠DCB′，从而得到

∠DBC＝，此时所以选A.

反思垂直、平行、平分等特殊情况，极大、极小等极端情形，就是将点、线、面的运动位置推到极限状况，从而把比较隐蔽的条件或临界状况暴露出来.事实上，由特殊到一般的本质就是归纳推理.所有偶然的背后不一定有必然作为支撑，但所有必然都是通过偶然表现的.

4 “猜想”探路，“证明”跟上

例4（2020年新高考卷理科第21题）已知函数f（x）＝aex-1-lnx+lna.

（ⅠⅠ）若f（x）≥ 1，求a的取值范围.

解析由于f（1）＝a+lna≥ 1，且y＝a+lna是单调递增的函数，所以a≥1.

下证:a≥ 1时，f（x）≥ 1恒成立.

令h（a）＝ex-1·a+lna-lnx，注 意 到y＝h（a）是单调递增的函数，所以h（a）≥h（1）恒成立.令g（x）＝h（1）＝ex-1-lnx.g′（x）＝ex-1-，注意到y＝g′（x）是单调递增，且g′（1）＝0，所以y＝g（x）在x∈（0，1）时 单 调 递 减 ，在x∈（1，+∞）时单调递增，所以g（x）min＝g（1）＝0，所以g（x）≥ 1恒成立，得证.

反思“必要性优先”的处理办法是十分有效的.学生看到这样的解法，一是感叹解法的简洁明了，二是感到疑惑，为什么一开始x要取值1，而不是其它的数.事实上，“必要性优先”处理的关键是能取到“好”的值.对于x＝1的得来，可以基于这样的猜想.

f（x）＝aex-1-lnx+lna≥1 恒 成 立 ，即aex-1≥lnx-lna+1恒成立，猜想

y＝aex-1和y＝lnx-lna+1有公共的切线和切点.设切点横坐标为x0.则有

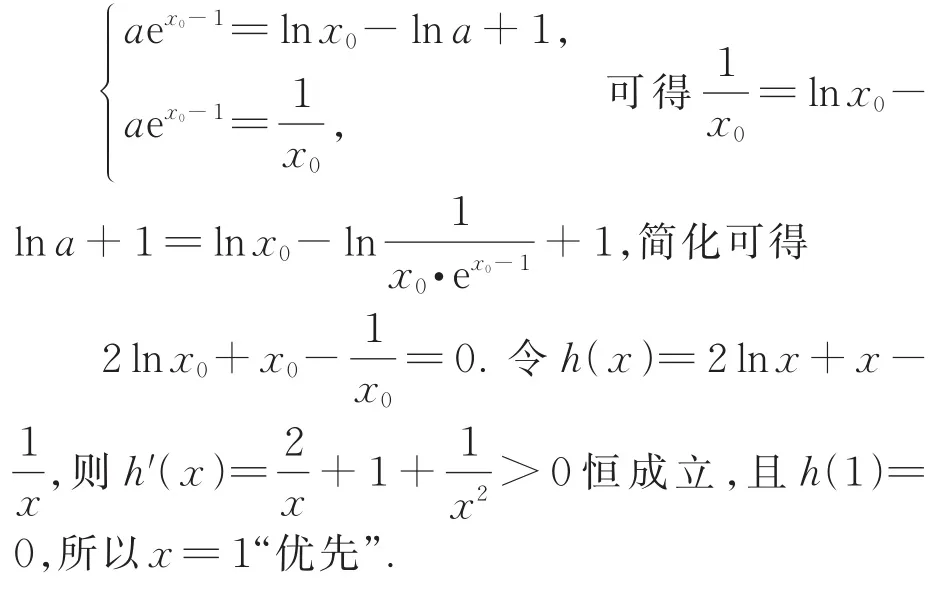
由归纳推理得到的结果不一定正确，但指引了问题研究的方向.这就要求我们在应用归纳推理解决问题时，不妨大胆“归纳”，务必小心“求证”.