考虑空间参数随机特征的沥青路面力学行为分析
2022-02-28谭鹏
谭 鹏
(湖南建工交通建设有限公司, 湖南 长沙 410004)
沥青路面结构以其良好的工作性能受到欢迎,无论是在高速公路还是其他等级公路中都得到了广泛应用,但是在沥青路面结构设计过程中,为了简化设计过程忽略了沥青混合料表现出的各向异性,这种情况会导致沥青路面在使用寿命期间出现预期之外的路面病害。
在我国规范中将沥青路面视为各向同性弹性多层体系,并将层间接触状况视为完全连续,在垂直均布静载作用下验证强度,这样的形式能够简化设计过程,但显然无法准确描述沥青路面真实工作状态下的受力情况,根本上的问题就是忽略了沥青路面结构的各向异性,这会对其力学性质有错误的估计。Levenberg等[1]对沥青混合料试件进行实验室中的静压测试,结果表明沥青混合料在竖直方向上的强度是水平方向上的1.56倍。Wang等[2]对现场压实沥青采样研究,进行了各向同性压缩及三轴拉伸试验等多个测试,发现垂直模量是水平模量的2~5倍。鞠达[3]对AC-20混凝土从垂直和横向两个方向进行取芯,中粒式沥青混凝土横向试样模量仅为竖向的80%。因而对沥青路面结构设计的各向同性简化是有缺陷的,在集料的影响下,沥青混凝土不可能是连续均值材料,我们有必要研究清楚沥青混凝土的各向异性,改善现有设计过程。
为此,本文将针对沥青混凝土路面结构建立参数随机场与有限元模型,模拟沥青混合料表现出的各向异性。模型建立的沥青路面回弹模量参数随机场为对数平稳随机场,随机场的数字特征不随空间位置变化,进行有限元模型计算后将结果与均匀场进行对比,分析沥青路面结构设计中忽略沥青混合料各向异性对路面结构工作情况的影响。
1 平稳随机场参数模型
1.1 平稳随机场介绍
沥青混合料的各向异性是由于集料的大小不一和不均匀排布造成的,即使集料粗细程度相同的沥青混合料在物理力学性质上也存在差异,故其回弹模量参数是具有不确定性的,但是这种不确定性也并不是完全随机的,沥青路面结构参数具有空间参数相关性,因此在分析中应该考虑相关性与随机性两种性质。
引入随机场理论对沥青路面结构参数的相关性与随机性两种性质进行分析,平稳随机场参数的均值与方差不随路面空间位置而变化,方差只与空间中两点的相对位置有关,而与绝对位置无关,符合沥青混合料各向异性造成的参数随机性。目前有很多方法可以生成随机场模型,本文采用协方差分解法建立平稳随机场,由数据的均值、方差及相关距离三个参数就可以用协方差分解法构建一个平稳随机场。协方差分解法可以高度精确地生成随机场,而且协方差分解法可以比较容易地实现随机场模型到数值的一对一单元映射,十分适合本研究中使用有限元软件分析。
协方差分解法最重要的环节就是协方差矩阵的构建,假设xi,xj(i,j=1,2,…,n)为随机场中的离散点,τij为任意两点xi,xj之间的相对距离,C为n个点之间的协方差所组成的n阶协方差矩阵,该矩阵为一正定矩阵,矩阵C中任一元素cij为xi,xj之间的协方差,cij=c(τij)。对协方差矩阵C进行Cholesky分解得到上三角、下三角矩阵:
C=LU=LLT
(1)
式中:L为下三角矩阵;U为上三角矩阵。设Y为由n个相互独立且服从标准正态分布的随机数所组成的列向量,则n阶随机场矩阵Z可以表示为:
Z=LY
(2)
随机场矩阵Z中任意点zij服从标准正态分布,且协方差矩阵E(ZZT)=E(LYYTLT)=C,满足相关性要求,因此矩阵Z可以作为正态平稳随机场的一次实现。对矩阵Z进行数学变换可以得到任意不同分布形态的正态和对数正态平稳随机场。多次随机生成服从标准正态分布的矩阵Y,就可以形成随机场的多次实现。
1.2 相关距离计算
相关距离概念联系的是空间相关性这一性质,即在沥青路面结构中相距一定距离的两点参数正好具有一定相关性,而在这两点之外的点参数不再具有空间相关性,这个极限距离即为相关距离。
介绍相关距离必须先定义方差折减函数,如式(3)所示。
(3)
式中:Γ2(s)为方差折减函数;D(Xs(k))为均方根连续的平稳随机场的空间标准差;D(X(k))为标准差,D(X(k))=σ;var(Xs(k))为平稳随机场概率密度函数的二阶距。
相关距离结合方差折减函数来看,折减是在一定范围s之内,是一个递减函数,随着两点距离的增大,折减就越快,空间相关性就越低,而当距离越趋近于正无穷时,方差折减函数就越接近0,两点不再具有空间相关性。本研究分析空间相关性,是因为虽然两点在收集数据过程中是离散的,但在本研究中其作为路面结构整体中的一个小部分,即使沥青混合料中集料的不均匀排布产生参数差异性,也是有章可循的,每点之间具有一定程度空间相关性,方差折减函数正是用来表达两点之间的参数影响。而有一点是显而易见的,相距越远,其相关性就会越低。
相关距离参数a,b可以通过以下步骤求解:
(1)对于收集到的离散数据,计算出其均值函数E[X(s)]以及方差σ2;
(2)先令i=2,将相近两个数据组成一组数据,求出该组新组成数据的均值和方差D2(2);
(4)将上一步中计算得到的数据绘入散点图;
(5)令i=3,4,…,重复(2)~(4)步骤,绘制出较为完整的Γ2(i)曲线;
(6)将绘制成的Γ2(i)图拟合成线,找出其趋于平稳的点,取为计算值,按δ=sΓ2(s)(δ为两点间的相关距离,s为此时两点间的距离)可求解出相关距离。
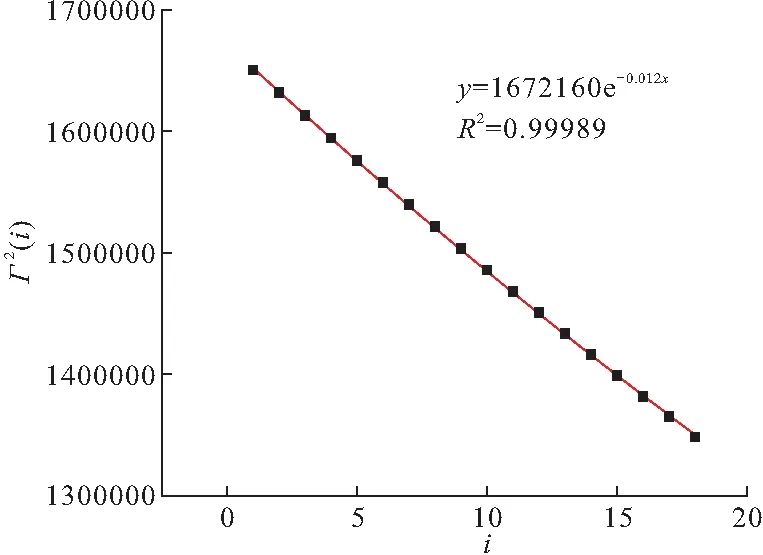
图1 相关函数曲线
再根据Γ2(i)图中拟合得到的指数函数分析出其后续变化情况如图2所示。
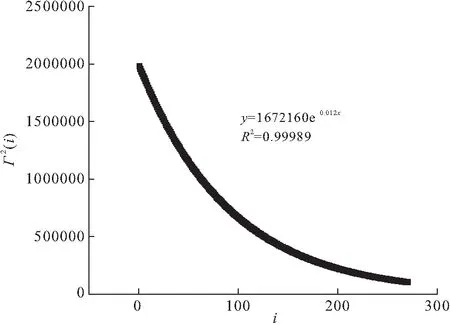
图2 相关函数拟合曲线
可以看到大概在i取值为260后Γ2(i)变化不大,根据平稳点计算得相关距离为24.6 m,计算过程如式(4)所示。
(4)
抑或是在拟合了相关函数后,可以根据图中曲线选取指数型相关函数ae-b|τ|时,相关距离为16.8 m,计算过程如式(5)所示。
(5)
式中:δ为相关距离;b为相关函数中的系数。
两个结果之间相差还是比较大的,其主要原因是因为样本数较少,而根据拟合建立的数据样本又可能并没有办法真实表述沥青路面参数情况。前面有提到随机场理论中相关距离的概念可以指导施工过程中的钻芯取样,使两个芯样之间间距比较合理,但在建立随机场的过程中,钻取芯样越多、越密效果会越好,计算结果会更加准确。
最终根据公式计算,取相关距离为δ=16.8 m。
1.3 平稳性检验及各态历经性检验
要完全表达一个随机场的分布函数簇是十分困难甚至是不可能完成的,所以可以用随机场的统计特性来建立随机场。建立一个平稳随机场只需要数据均值、标准差及相关距离三个统计特性,而为了验证根据统计特性建立的随机场是否具有代表性,建立完成之后必须进行平稳性检验和各态历经性检验。建立的随机场回弹模量分布如图3所示。
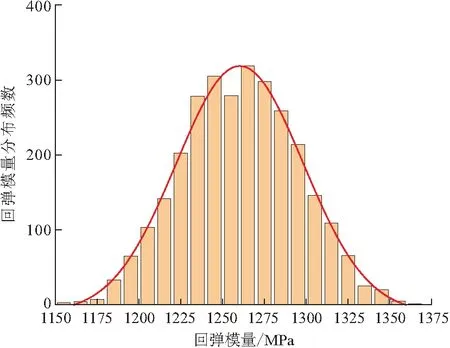
图3 随机场回弹模量分布
随机场理论实际上是一种对数据的处理方法或者说一种思路,在沥青路面参数方面,区别于其他数据处理方法的地方在于引入了相关距离这个概念,前面也提到过相关距离确实在工程中有一定指导意义,但相关距离概念更多是停留在理论阶段,要结合到实际工程中,需要对随机场进行平稳性检验和各态历经性检验。
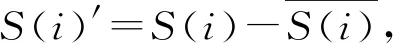
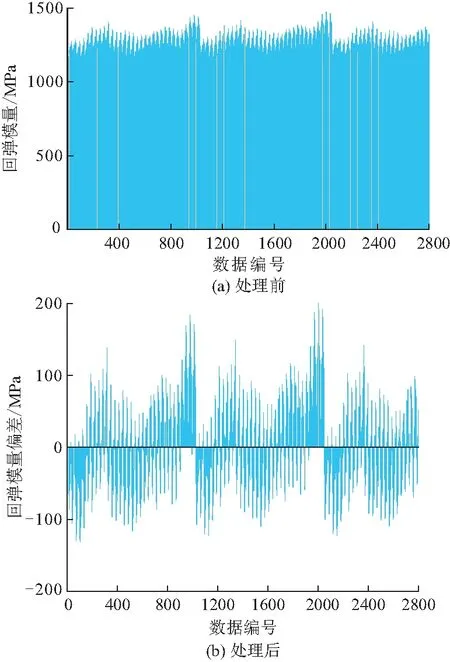
图4 数据处理前、后对比
平稳随机场的平稳性体现在数字特征不随空间位置的变化而变化,具体体现在随机场的均值函数不会随着数据组的改变而出现极大变化或规律性增加或减少。定义了集平均和深度平均的概念,面对具体数据时,任一组数据中某一行sj上随机场数据的集平均可表示为:
(6)
X(sj)与X(sj+Δs)的相关函数可表示为:
(7)
式中:i为一组数据中的数据个数,模拟不同钻孔取芯位置;j为数据组中的行数,模拟钻孔芯样的不同深度上的数据。根据随机场平稳性的定义,平稳性检验步骤如下:
(1)取数据组中一行sj如j=1,再找出不同的i取值对应的回弹模量数据Xi(s1),i=1,2,…,n;还有与其间距为Δs的数据s1+Δs处的数据Xi(s1+Δs),i=1,2,…,n;
(2)利用式(6)(7)求出均值μx(sj)与相关函数RX(sj,sj+Δs);
(3)令i=2,3,…,m,重复步骤(1)~(2),计算出所有均值μx(sj)与相关函数RX(sj,sj+Δs)的值,并绘制成散点图;
(4)检验均值μx(sj)与相关函数RX(sj,sj+Δs)的散点图是否随数据组编号增加而发生明显变化,若未观察出明显变化则说明随机场平稳,否则不平稳。
检验结果如图5所示,表明所建立的沥青路面参数随机场模型中回弹模量与相关函数并不随数据组变化而发生太大波动,可视作无变化,即随机场模型的均值函数μx(sj)为常数,等于0。
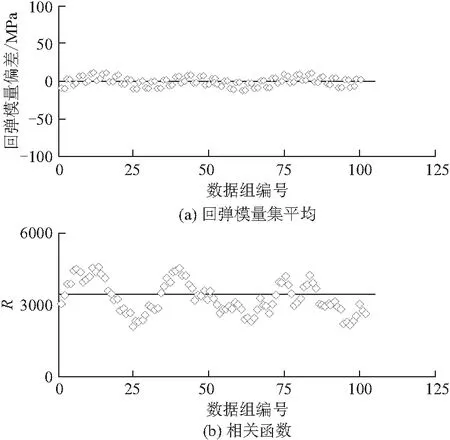
图5 平稳性检验结果
沥青路面相当于一个极其庞大的随机过程,其中每一点的参数都是不确定的,随机场模拟过程就是根据测到的个别点的参数来分析路面中每一点的参数。这个过程中用以建立随机场的点在整个沥青路面中只占极其少的一部分,那么这一小部分点就应该具有较大的代表性,能够充分代表整个沥青路面结构,这种代表性即为随机场的各态历经性。在处理具体数据时,根据定义,任一组数据中某一行sj上随机场数据的深度平均〈Xi(s)〉可表示为:
(8)
对于一组数据,取固定Δs,则Xi(s)Xi(s+Δs)也是平稳随机场,则有深度平均〈Xi(s)Xi(s+Δs)〉的深度均值可表示为:
(9)
式中:i,j定义与平稳性检验中相同。根据随机场各态历经性的定义,各态历经性检验的步骤如下:
(1)取数据组中一列si如i=1,再找出不同的j取值对应的回弹模量数据X1(sj),还有与其间距为Δs的数据sj+Δs处的数据X1(sj+Δs),j=1,2,…,n;
(2)利用式(6)(7)求出均值〈μx(sj)〉与深度相关系数〈RX(sj,sj+Δs)〉;
(3)令j=2,3,…,m,重复步骤(1)(2),计算所有均值〈μx(sj)〉与深度相关系数〈RX(sj,sj+Δs)〉的值,并绘制成散点图;
(4)检验深度均值〈μx(sj)〉与深度相关系数〈RX(sj,sj+Δs)〉的散点图是否随数据组编号增加而发生明显变化,若未观察出明显变化则说明随机场具有各态历经性,否则不具有各态历经性。
检验结果如图6所示,表明所建立的沥青路面参数随机场模型中深度平均与深度相关系数并不随数据组变化而发生太大波动,可视作无变化,即随机场模型具有各态历经性。
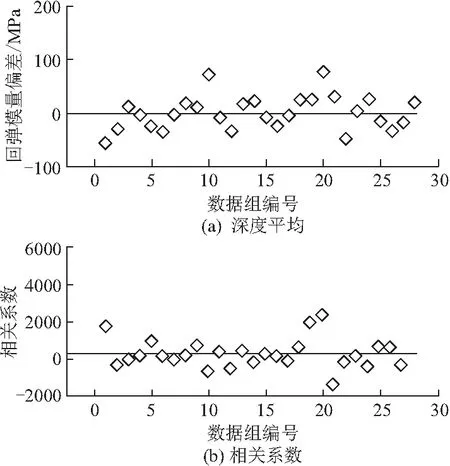
图6 各态历经性检验结果
2 路面有限元模型建立
2.1 有限元模型
最终建立尺寸为4.5 m×4.5 m×6 m的有限元模型(x,y,z),x为道路横向,y为道路纵向,z为道路深度方向。均布荷载作用在模型中心区域,模型荷载使用标准轴载BZZ-100计算得来,对0.45 m×0.45 m区域施加770 MPa压强。通过协方差分解法建立弹性模量随机场模型,将对应弹性模量随机场信息映射到有限元计算模型中,得到考虑沥青混合料弹性模量随机特征的计算模型。值得注意的是,为了有限元模型的网格能够嵌入随机场参数,并不在受力面层及受力区域进行加密,而是采用均匀网格。水平面横、纵向边具有32个结点,深度方向竖向边具有81个结点,总共82499个节点,76880个单元。单元使用C3D8R八结点六面体线性缩减积分单元。面层模型部分边界限制道路横向x和纵向y的位移,基层模型部分边界限制道路横向、纵向和深度方向上的位移。模型尺寸、边界条件及荷载情况如图7所示。
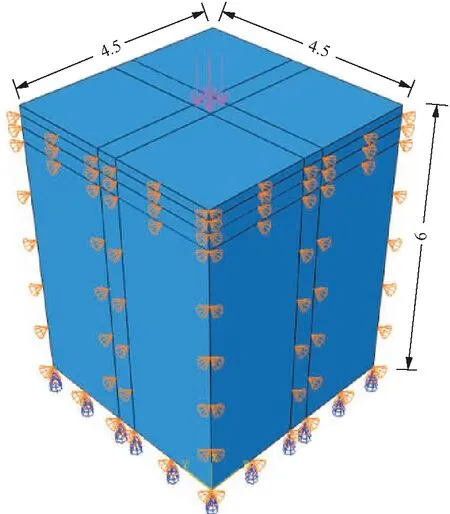
图7 沥青路面有限元模型/m
2.2 路面结构及材料参数
在有限元计算分析过程中采用四层结构组合的路面结构形式,从上往下依次是沥青面层、水泥稳定碎石基层、水泥稳定土底基层及土基,各层路面结构层间连续,将沥青面层考虑为各向异性材料,使用参数随机场模拟其各向异性,其余部分回弹模量参数如表1所示。

表1 有限元模型材料参数
沥青路面结构面层中单元仍然是各向同性连续单元,但每个单元的回弹模量为随机场中参数,模拟出由于沥青混合料中集料大小不一与分布不均匀导致沥青混合料表现出模量分布的空间随机特征,大致情况如图8所示,图中Ea为沥青面层材料弹性模量,其不同颜色代表模型中弹性模量的空间分布情况。
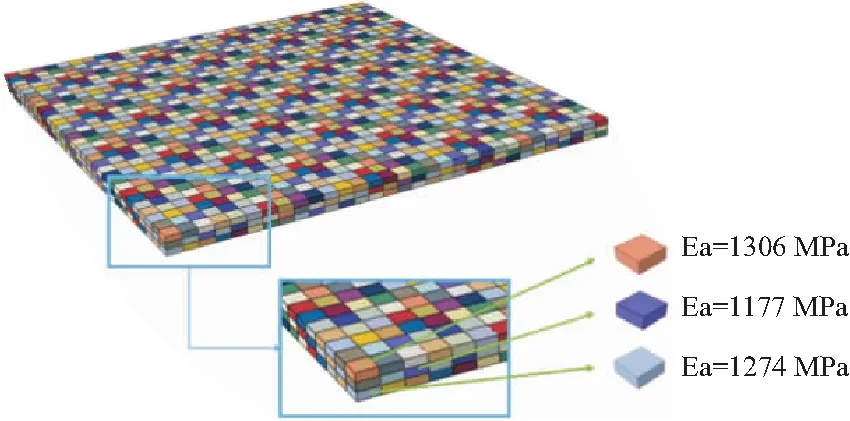
图8 沥青路面面层
3 空间参数随机特性的影响分析
3.1 确定性分析
采用有限元软件计算沥青路面结构模型,对计算结果主要分析计算结果的三个参数,面层层顶竖向位移、面层层底拉应变及层底拉应力,通过这三个参数可以比较好地看出,引入随机场理论来模拟沥青混合料各向异性后对沥青面层工作状况的影响,讨论在结构设计、实际施工过程中考虑沥青混合料各向异性的必要性。
提取分析有限元软件ABAQUS的计算结果, 先从剖面分析,随机场模型产生的面层层底最大拉应力、层底最大拉应变及层顶竖向位移如图9~11所示。
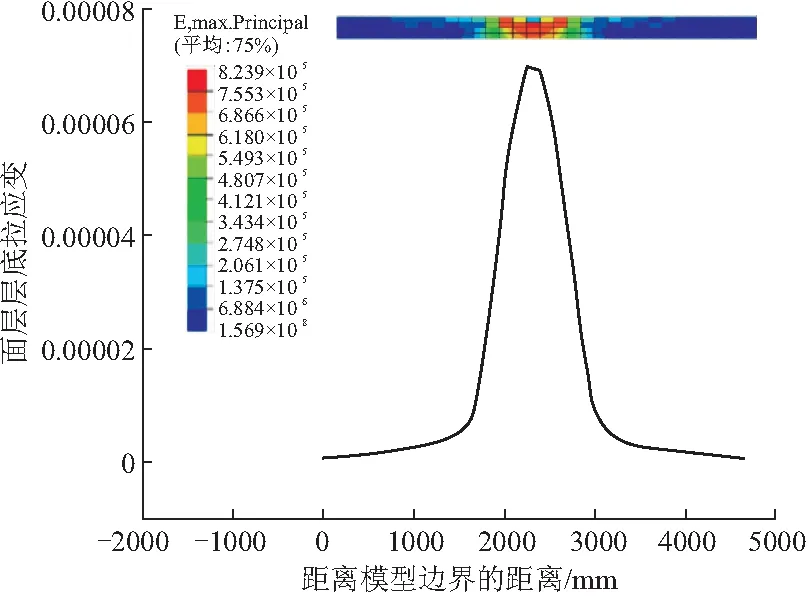
图9 随机场模型沥青面层层底拉应变
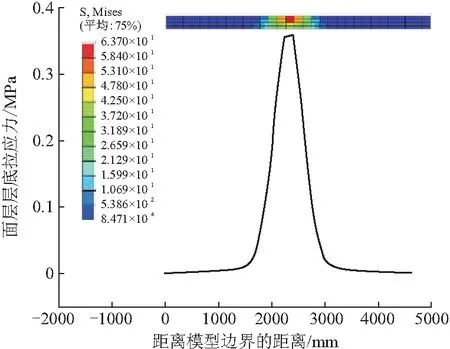
图10 随机场模型沥青面层层底拉应力

图11 随机场模型沥青面层层顶竖向位移
随机场模型剖面层底拉应力、层底拉应变及层顶竖向位移均呈现出先增大后减小的变化,在荷载中心附近达到最大值,两侧数值较小,符合各种参数变化的规律。在整体上对比随机场与均匀场模型中应力、应变及竖向位移最大点,分析结果如表2所示。
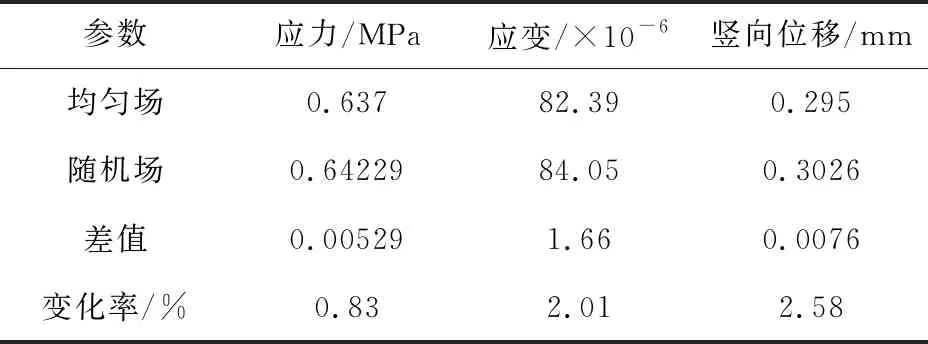
表2 均匀场与随机场应力、应变及竖向位移对比
随机场模型中最大应力比均匀场模型大0.83%,最大应变比均匀场模型大2.01%,最大竖向位移比均匀场模型大2.58%。
3.2 随机性分析
随机场生成过程中有生成随机数的部分,虽然在数值上影响不大,但是必须避免随机过程中出现比较极端的数据,使得研究数据不再具有代表性,导致分析出的结果出现偏差。所以有必要建立多个随机场,对数据进行对比,避免所生成的随机场参数不合理的情况,使得本研究具备更高的可靠性。随机场模型产生的层底最大拉应力、层底最大拉应变及层顶竖向位移与均匀场对比如图12~14所示。
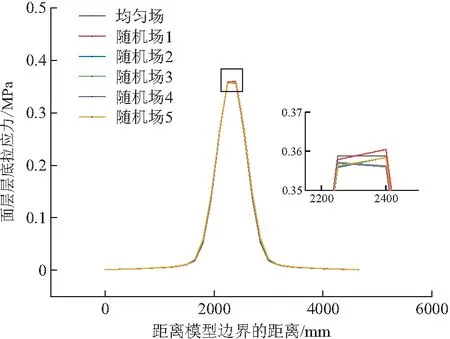
图12 面层层底应力对比
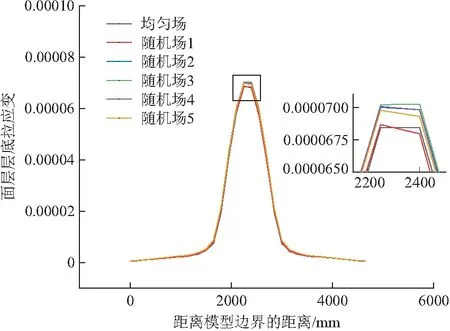
图13 面层层底拉应变对比
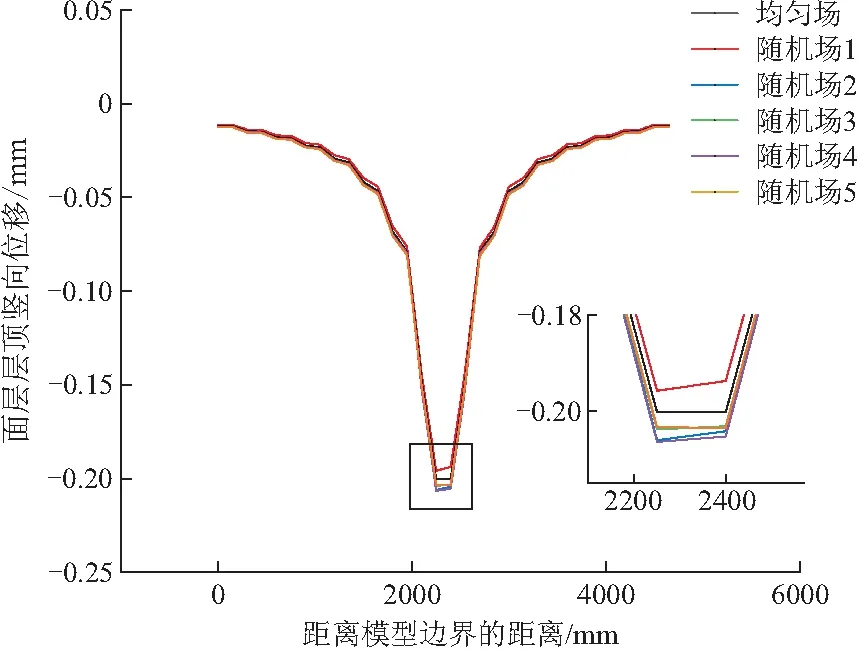
图14 面层层顶竖向位移
对受力单元层底应力参数进行分析,随机场中最小值较均匀场小0.68%,最大值较均匀场大2.58%。由此可见,沥青路面结构参数随机性对沥青路面层底应力有明显影响。
对受力单元层底应变参数进行分析,均匀场层底应变参数在均匀场中为0.3587,随机场中层底应变最小为0.3558,较均匀场小0.8%,最大为0.3584 mm,较均匀场大0.4%。由此可见,沥青路面结构参数随机性对沥青路面层底应变有一定影响,但不显著。
对受力单元层顶竖向位移参数进行分析,均匀场层顶竖向位移参数在均匀场中为0.2 mm,随机场中层顶竖向位移最小为0.1938 mm,较均匀场小3.25%,最大为0.2065 mm,较均匀场大3.11%。由此可见,沥青路面结构参数随机性对沥青路面层顶竖向位移有显著影响。
4 结 论
(1)将随机场理论运用到沥青路面结构中,通过平稳随机场模拟沥青混合料的各向异性并对结果进行分析,证明这种方法的可行性;
(2)考虑沥青混合料各向异性,对沥青路面结构面层层底应力影响较小,对层底应变及层顶竖向位移有一定影响;
(3)现行路面设计理论中,将结构层材料考虑为各向同性明显高估了沥青路面结构稳定性,使沥青路面结构更容易出现沥青路面病害,应当在设计过程中考虑到沥青混合料各向异性的影响。
