海底单层管道铺管端部受力数值分析*
2022-02-28马国锐刘永升孙宇宸徐晓楠
马国锐 刘永升 孙宇宸 徐晓楠
(1.中国石化西北油田分公司石油工程技术研究院 2. 中国地质大学(北京)工程技术学院)
0 引 言
海底单层管道是海上油气田开发生产系统的主要组成部分,也是目前最快捷、最安全和经济可靠的海上油气运输方式,其结构是在3PE管道表面涂敷一层混泥土配重层。混凝土配重是一种有效克服海洋浮力防止漂移的方法,同时混凝土层具有良好的抗机械损伤性能,能适应恶劣的海底环境和承受外力的损害。随着我国海上油气资源勘探的深入,必然需要建设高效、经济、便捷的输送管网[1]。目前,我国海底单层管道的涂覆配重工艺基本依赖与国外公司的合作[2],对海底管道的整体受力特性、钢筋混凝土配重层粘结滑移以及各层之间的相互作用机理的认识尚不透彻,无法更好地指导铺管操作以防止管道受损。因此,研究管道在铺管工况下的受力状态,钢筋-混凝土、钢管-混凝土的粘结滑移大小及规律,对正确认识海底管道混凝土层开裂、裂纹分布以及裂纹扩展具有重要意义。
钢筋与混凝土、混凝土与钢管之间复杂的交互作用,主要依靠相互间的粘结应力(即接触面上的剪应力),其中钢筋整体嵌入混凝土土体中,而混凝土与钢管之间通过面-面接触传递应力和协调变形,上述两种作用方式的粘结强度主要由水泥凝胶体与钢筋、钢管表面的化学胶着力,混凝土与钢筋、钢管之间的摩擦力以及机械咬合力3部分组成[3],也正是基于这3种耦合作用将海底管道连为一体,实现其防漏、承压和置底的功能。试验结果表明,混凝土的应力状况、裂缝的形成与发展、钢筋应力状态以及钢筋、钢管与混凝土间的粘结滑移等均受到三者交界面性质的影响,而且破坏机理相当复杂。自从Y.HAMMATY等[4]首次借助非线性弹簧单元进行粘结滑移数值模拟以来,国内学者王依群等[5]、刘佩玺等[6]和赵卫平[7]也采用同样的方法实现了对混凝土梁以及不同温度下粘结-滑移性能的数值模拟,并且取得了良好的效果。
本文采用ANSYS非线性有限元分析方法,引入combin39三维非线性弹簧单元来模拟钢筋与混凝土之间的粘结力和咬合力,并通过目标单元TARGE170、接触单元CONTA173实现钢管与混凝土界面的协调耦合,从而进一步了解海底管道在受力特性下的相对滑移和开裂。
1 粘结滑移有限单元模型及锚固方程
海底配重管道(见图1)混泥土层锚固钢筋的平面受力状态的表述如图2所示。初始状态钢筋单元节点和混凝土单元节点重合,受力后由于钢筋和混凝土的相对滑移,原来重合的节点发生横切向的错移。粘结锚固基本变量及相互关系如图3所示。拉力Fl引起钢筋应力σs(x)和应变εs(x),因界面粘结应力τ(x)传递而引起混凝土应力σc(x)和应变εc(x),应变差产生相对滑移S(x),取微段dx分析受力及变形,可建立粘结锚固基本方程[8]。

1—纵筋;2—混凝土层;3—钢管;4—3PE层;5—箍筋。
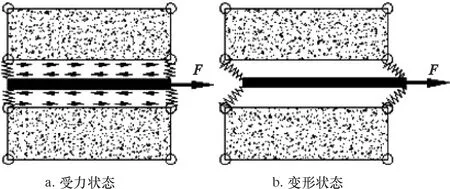
图2 有限单元模型
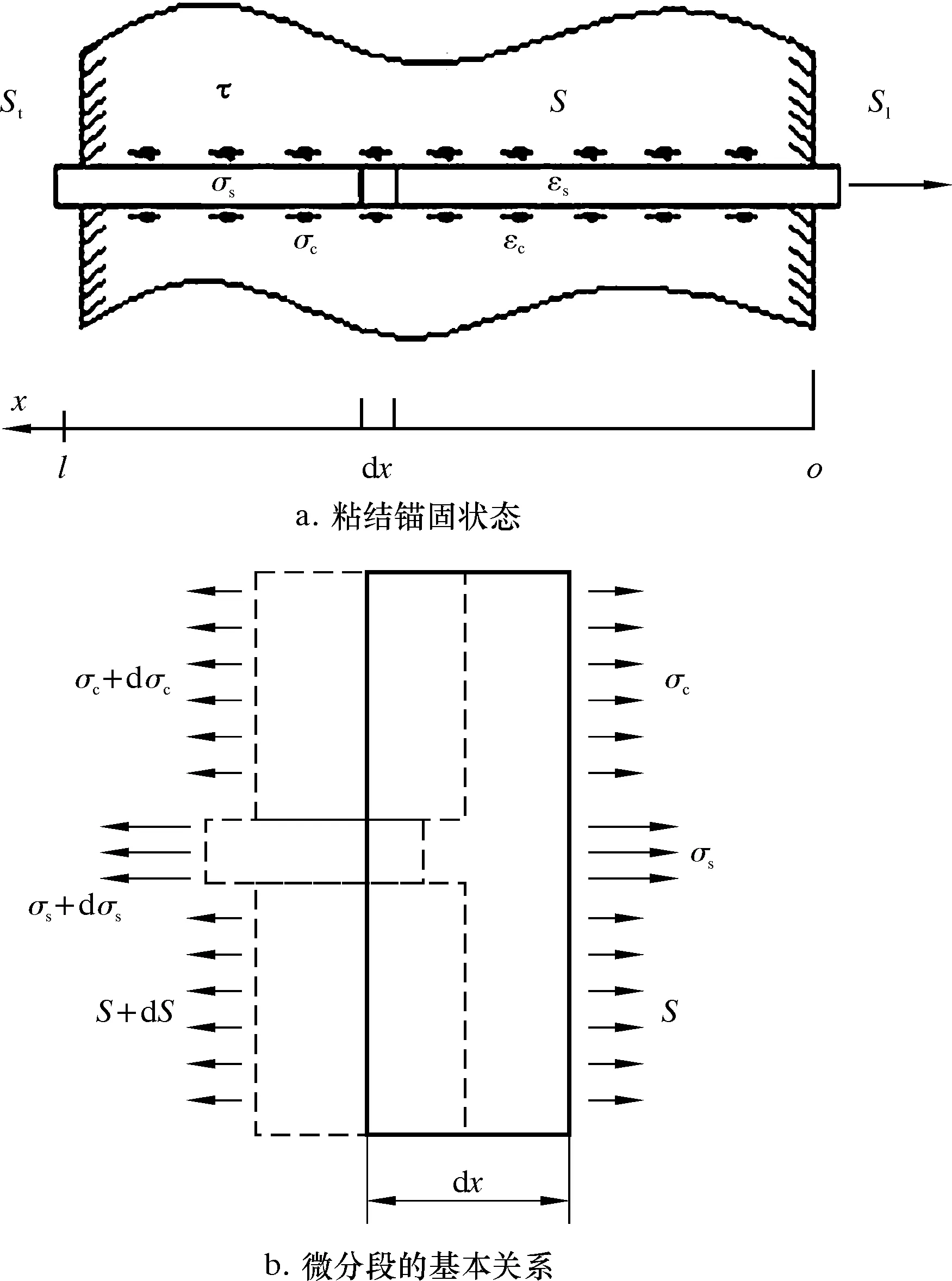
图3 粘结锚固基本变量及相互关系
平衡方程为:
(1)
(2)
变形协调方程为:
dS=(εs-εc)dx
(3)
物理方程为:
σs=f1(εs)
(4)
σc=f2(εc)
(5)
τ=φ(S)·ψ(S)
(6)
式中:φ(S)为τ-S关系式,ψ(S)为位置函数,d为钢筋直径,As为钢筋截面积。
由积分可求钢筋内力N(x)及滑移S(x),即有:
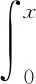
(7)
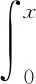
(8)
2 裂缝表征模型
混凝土的承压性能远大于抗拉特性,所以海底管道在装管、铺管及工作状况下受波流引起弯曲,受拉部位易出现裂纹,从而使结构性能发生重大变化,这也是造成结构非线性的另一重要因素。目前常用的裂缝模式主要有[3]:①利用单元边界模拟裂缝的分离式裂缝模型;②利用单元内部材料本构关系模拟裂缝的分布裂缝模型;③通过改造单元形函数构造内嵌裂缝的特殊单元模型。
分离裂缝模型是把裂缝处理为单元的边界,将节点分置于裂缝的两侧(见图4a),当中心的裂缝产生时就增加新的节点,重新划分单元,使裂缝重新处于单元边界上。这种模式可以细致模拟裂缝发生的过程,得到每条裂缝宽度和长度等数据。分布裂缝模型是以在一个区域内均匀分布的相互平行的微细裂缝来代替单一的裂缝(见图4b),裂缝出现后,只需对材料的本构矩阵加以修正,仍可同裂缝出现前一样,把材料作为连续介质处理,这种裂缝模型,裂缝能够自动形成,不必增加节点和重新划分单元,计算可以自动连续进行。鉴于分布裂缝模型的优点,该研究采用该裂缝模型进行模拟。

图4 裂缝模型
3 分析模型
3.1 材料模型
3.1.1 钢筋、钢管材料模型
为使分析更接近实际,钢管以及加载支座采用多折线线性随动强化模型(MKIN)[9],纵筋和箍筋采用双折线线性随动强化模型(BKIN),其中弹性模量、屈服强度和极限强度按表1选取,忽略温度对钢材性能的影响。

表1 钢筋材料参数
3.1.2 混凝土材料模型
鉴于混凝土材料的复杂性,诸多学者对混凝土材料的本构关系做了研究,也取得了很多成果,但是还没有一种理论模型被公认为可以完全描述混凝土材料的本构关系。本文研究中,混凝土的本构关系采用《混凝土结构设计规范》中的单轴受压应力-应变曲线和单轴受拉应力-应变曲线。
混凝土单轴受压应力-应变曲线方程为:
(9)
式中:αa、αd分别为单轴受压应力-应变曲线上升段与下降段的参数值。
混凝土单轴受拉应力-应变曲线方程为:
(10)
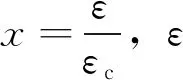
将应力-应变曲线简化成多段折线,按照非线性弹性材料模型输入,该模型能准确地与试验吻合[10]。混凝土破坏准则采用ANSYS程序中默认的William-Warnke五参数破坏准则[9]。
3.2 单元类型选择
3.2.1 实体单元
ANSYS中的solid65单元[11]可模拟混泥土拉裂、压碎、塑性变形及徐变的功能,本文利用该单元的实体性能来模拟混凝土。钢管采用solid45单元,而用管单元pipe20模拟纵筋和箍筋的拉伸、压缩、塑性变形及蠕变。pipe20是单轴弹性管单元,具有拉压、扭转和弯曲性能,同时可直接绘制钢筋主应力和等效应力云图。用pipe20单元模拟时,将钢筋直径D作为管单元的外径OD,而管单元的壁厚WTHK取钢筋半径r减去一很小值e。
3.2.2 基于Houde粘结滑移公式的combin39力学模型
在海底单层管道结构有限元分析中,考虑钢筋与混凝土粘结滑移行为,引入连接单元(combin39),目的是正确反映钢筋混凝土间的粘结滑移本构关系。在钢筋和混凝土对应节点之间横切向采用combin39单元形成连接单元,弹簧单元代表连接面上横切向的相互作用,单元长度均为0。
试验得到的粘结应力与滑移间的四阶关系式为[12]:
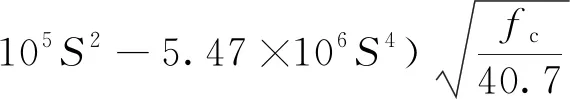
(11)
式中:τ为粘结应力,MPa;S为相对滑移量,mm,在滑移量达到0.03 mm左右时,粘结应力达到最大值;fc为混凝土轴心抗压强度,MPa。
对于钢筋混凝土有限元模型,粘结力F与滑移量S的关系如下:
F(S)=πdlτ(S)
(12)
式中:d为一根钢筋的直径,l为联结单元间距。
由此可以得到沿锚固方向弹簧单元的载荷-位移,其关系式为:

(13)
3.2.3 基于库伦摩擦模型的接触单元
在钢管和混凝土的界面上插入界面单元,采用面-面接触单元,刚度较大的钢管表面被当作目标面,采用Targe170单元模拟三维的目标面,刚度较小的混凝土表面被当作接触面,采用contal174单元模拟,目标单元与接触单元设置相同的实常数。界面接触单元支持库伦摩擦模型,在基本的库伦摩擦模型中,2个接触面在开始相互滑动之前,在他们的界面上会有某一大小的剪应力产生,这种状态被称作粘合状态。库伦摩擦模型定义了一个等效剪应力τ,在某一法向压应力p作用下,剪应力达到此值时表面开始滑动。
τ=μp+COHE
(14)
式中:COHE为粘聚力,μ为摩擦因数。本文忽略温度对摩擦因数的影响,取μ=0.45[7]。
3.3 几何模型建立及有限元模型的生成
3.3.1 工程背景及几何模型
本次数值模拟源于工程实际中海底管道铺管过程中张紧器端管道的受力分析,管道一端由张紧机构固定,另一端通过弧形托管架下放至海底。张紧器铺管模型如图5所示。参照海底配重管道规格,这里取ø600 mm×9 000 mm管道进行数值模拟,其中混凝土层厚100 mm,钢管壁厚20 mm,纵向布筋16根,箍筋49圈。管道几何模型如图6所示。

图5 张紧器铺管模型

图6 几何模型
3.3.2 有限元建模
在进行有限元模型建立的过程略去防腐层的厚度(2~3 mm),混凝土单元首先借助平面网格单元plane42生成二维平面网格,通过拉伸形成3D网格模型,在混凝土两层单元交汇的共节点处,选择恰当位置生成钢筋单元;钢管通过实体建模,划分网格,得到钢管的网格模型;combin39弹簧单元在纵筋单元与混凝土单元重合的节点处生成,其长度为0,方向指向模型中的横切向,即Z向;依据平面假设,X、Y方向二者是协同应变,所以通过cpintf命令耦合重合节点处X、Y方向的自由度;钢管与混凝土接触单元通过建立接触对并设置相关的参数。其有限元模型如图7所示。
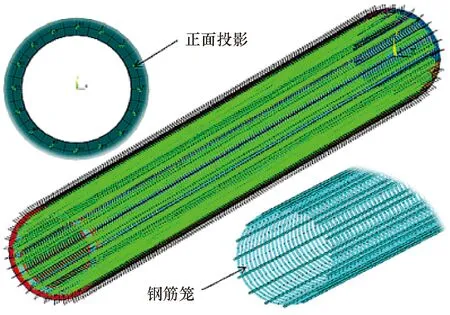
图7 有限元模型
3.4 约束及加载
根据实际铺管工况,该处管道一端受到张紧器的固定约束,另一端受到来自下放到海中管道的拉张力,以及管道沿弧形托管架的弯曲载荷。在上述载荷作用下,很容易引起混凝土配重层受拉区的开裂和受压区的压碎,同时诱发钢管与混凝土接触表面、钢筋与混凝土接触表面的相对滑移,导致防腐层的破坏和混凝土配重层的脱落,从而丧失力学保护性能。该分析中设置与张紧器接触部分的表层节点为固定约束,另一管道端面加载180 kN的拉张力[13],方向沿该处管道曲率的切线方向,并按托管架的实际曲率在管道下端设置刚性约束面。整体模型考虑重力因素,施加X方向9.8 m/s2的重力加速度。
4 计算结果分析
4.1 应力结果分析
4.1.1 管道整体应力
图8为管道整体应力云图。图9为管道应力矢量图。从图8可以看出:管道的应力分布主要呈现由张紧器固定端高应力区逐渐向下放端低应力区缓和,并且管道整体应力相对于XZ平面对称分布,管道的这种应力分布趋势表明,在铺管作业时管道受力最危险的区域为张紧器固定端,该处承受到来自已经下放管道的拉张力和管道因弯曲所受的弯矩,容易造成管道的拉裂和受压屈曲;最大应力(21.6 MPa)出现在张紧器端,而最小应力(87 381 Pa)出现在距离下放端约处,该处已然避开了张紧器影响,并且管道未处在曲率变化较大的部位,管道下放端由于受到拉张力作用,出现了应力集中现象,但是在对管道整体分析时,可以忽略因为加载造成的局部应力集中;管道弯曲过程中,X轴正向受拉,X轴负向受压,但是受拉区域要大于受压区域,也就是说弯曲面并不是YZ平面,而是呈“八”字形。
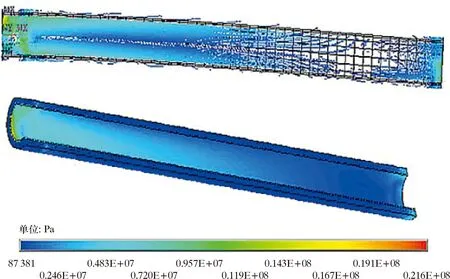
图8 管道整体应力云图

图9 钢管应力矢量图
4.1.2 纵筋应力分析
图10为不同部位纵筋沿管长方向的受力曲线。图10可以直观地反映不同部位纵筋应力分布规律:纵筋的应力分布总体趋势与管道应力分布一致,张紧器端应力居高,沿着管长方向应力递减;从图中各编号纵筋的应力曲线形状出发,可以将管道的受力分为3个不同的区域,编号为1#、2#、3#的纵筋应力-管长曲线形状呈抛物线状,其顶点位置代表张紧器右端固定位置,应力水平最大,这3根纵筋受力某种程度上代表了相应管道0°~50°扇形区域;编号为4#、5#、6#的纵筋应力-管长曲线除两端应力集中外,中间大部趋势平缓,应力水平在0.1~1.0 MPa之间,其表征管道50°~120°的扇形域;编号为7#、8#、9#的纵筋应力-管长曲线形似锯齿状连续缓降的驼峰,每个驼峰的顶点代表纵筋和箍筋交汇的节点,交汇节点一方面要制止相邻箍筋之间所包含的纵筋段滑移,另一方面该编号下的纵筋处在管道弯曲压缩区域,受到混凝土的强劲挤压,基于上述两者的作用共同导致交汇节点的应力较高,这3根纵筋包含在管道120°~180°扇形区内,主要特征为管道的受压;管道下放端纵筋的受力呈抛物线形,而处在拉压过渡区域、编号为5#的纵筋应力水平最高,位于抛物线的顶点。

图10 不同部位钢筋沿管长方向的受力曲线
4.2 位移结果分析
图11为管道一侧管长方向-X方向的位移曲线,整体形状大致为一大直径小区率的弧线,其下放端部相对于张紧器端竖直位移为4.61 mm。
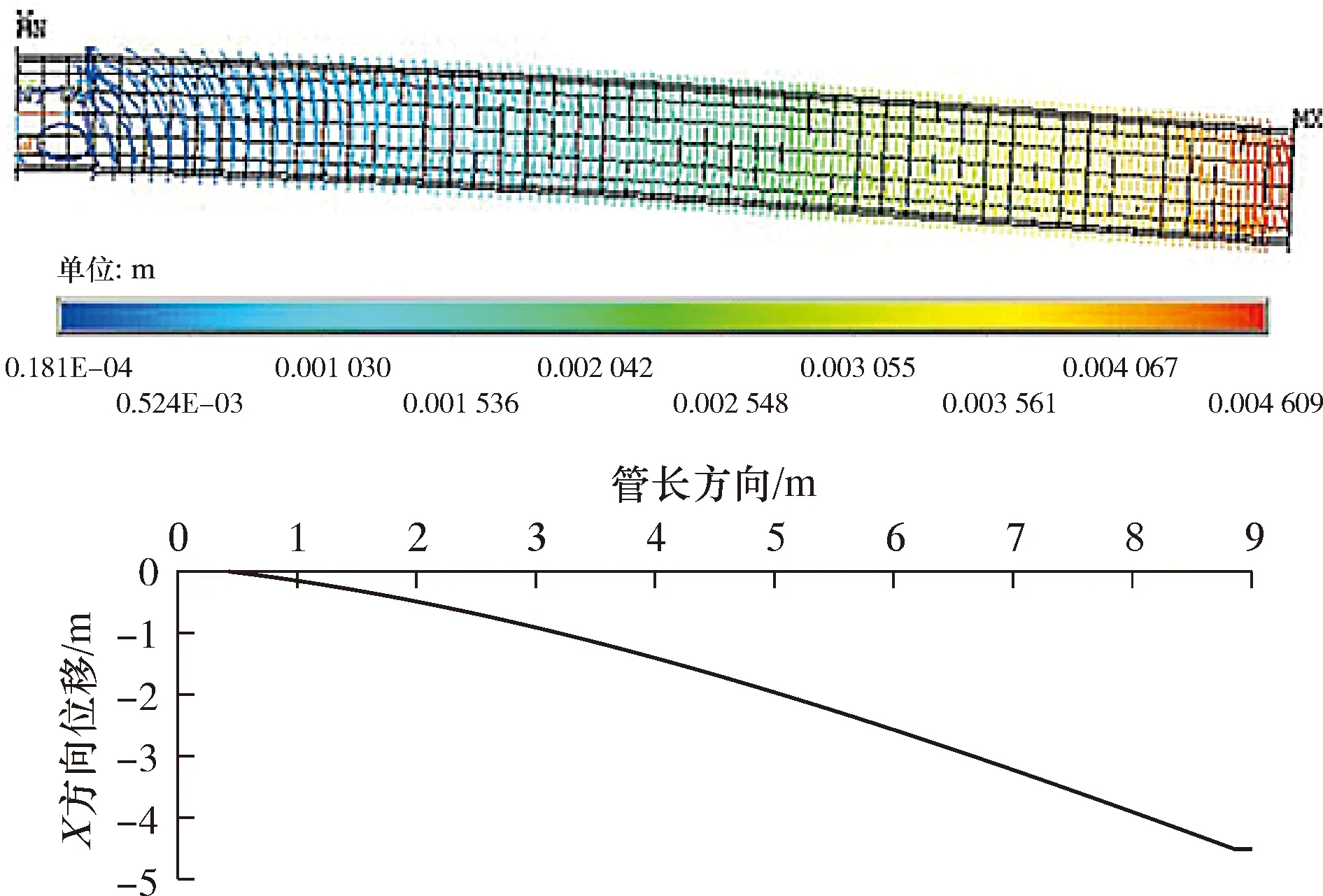
图11 管道X方向的位移
图12为管道一侧管长方向-Y方向的位移曲线,其位移大小总体在10-5m水平。从图12可以得出管道Y向位移大体可以分为3段:第一段为张紧器位置处,管道形变趋向发展成为截面形似椭圆状,该处Y向最大位移为1.5×10-5m;第二段为管道2~8 m,段管截面形状基本保持圆形,未发生明显的变形,管道的形貌保持完好;第三段为下放端,受集中加载拉张力以及下部受压影响,局部形变趋向发展成为类似椭圆状。

图12 管道不同部位Y方向的位移
4.3 不同方位钢筋滑移量
图13为管道不同方位钢筋的滑移量曲线。由图13可以得出:纵筋在混凝土中的滑移量最大的为9#,并且滑移量从管道的受压区向受拉区依次递减,最小滑移量的纵筋为3#,滑移量的大小在10-3mm数量级;在管长约0.5 m处,即张紧器所在的位置处,滑移量发生了突变,造成该种现象的原因主要是该处的混凝土配重层出现了拉裂破坏。
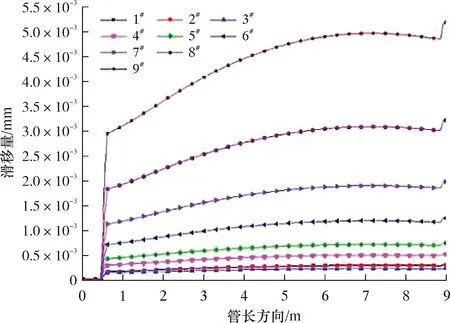
图13 管道不同方位钢筋的滑移量曲线
4.4 混凝土裂纹发展过程
图14为管道的裂缝形态发展过程示意图。通过模拟管道裂缝发展过程及工程实际铺管操作中裂缝发展过程对比分析[14-16],可以看出ANSYS计算所得裂缝分布基本上能反映工程实际铺管中混凝土配重管道裂缝出现的位置、先后顺序和裂缝发展的高度。

图14 配重管道裂缝主要形态及其发展过程示意图
4.5 接触压力及界面滑移
图15为钢管与混凝土配重层接触面的压应力云图。从图15可以看出,在张紧器固定端压应力较大,其次是在管道下放端由于加载造成了较高的接触压力。

图15 接触压应力云图
图16为钢管与混凝土配重层界面滑移量分布图。图16中X正向也即管道受拉区域,二者的相对滑移明显,零星散布高出其他接触区滑移量数量级的局部高滑移圈,最大滑移量为0.038 mm。
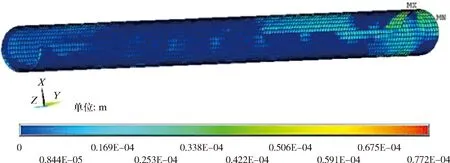
图16 界面滑移量
5 结论及认识
(1)提出的研究方法综合了目前关于钢筋混泥土结构数值模拟相关技术,其结果和工程实际吻合,可以为海底管道的设计和施工提供参考。
(2)通过开展对海底管道ANSYS数值模拟的研究工作,可以直观地显示钢筋应力云图,解决工程试验难以测得混凝土内部钢筋的应力的难题,可为寻找和得出钢筋的受力规律提供帮助,对合理布置钢筋有重大意义。
(3)数值模拟可以准确把握混凝土裂纹发展过程,可为改善张紧器加紧方式(如履带式加紧和分散受力部位)和防止裂纹产生提供帮助,还可以指导托管架曲率的合理设计。
(4)数值模拟可以获得界面滑移量,有助于改进界面接触方式,防止钢管与混凝土界面的相对滑移。
(5)对工程实际的真实模拟,可以减少试验费用,缩短设计周期,但是该数值模拟中所涉及的粘结滑移关系和界面相互作用相当复杂,还有待于进一步的研究并加以完善。
