直廓环面蜗杆传动的高次方修形原理
2022-02-27赵亚平李帅陈新元李公法
赵亚平,李帅,陈新元,李公法
(1.东北大学机械工程与自动化学院,辽宁沈阳 110819;2.武汉科技大学机械传动与制造工程湖北省重点实验室,湖北武汉 430081;3.武汉科技大学冶金装备与控制技术教育部重点实验室,湖北武汉 430081)
直廓环面蜗杆副最初由英国的Hindley 于1765年首先发明[1].1909 年,美国的Cone 进行了重要改进.实际上在此之前,德国的Lorenz博士就制成过这种蜗杆副,并取得了专利权[2].
与包络环面蜗杆副相比,直廓环面蜗杆副主要优点为:1)一般不存在边齿变尖[3].2)在轴截面内,相应蜗轮环面滚刀的齿廓为直线段[4],有利于刀具检验和测量.但也存在一些不足之处[5]:1)其蜗轮齿面上接触区面积较小.2)蜗杆螺旋面是不可展的直纹面,难于按成形原理精确磨削.
直廓环面蜗杆传动有原始型和修正型之分.原始型传动由于蜗轮齿面上存在所谓的“常接触线”,容易造成蜗轮的早期失效,多不主张采用[6].修正型传动按原理可以归结为基于实测磨损量的自然修形,和基于啮合理论的理性修形.其中前者属于半经验半解析的修形方法.
自然修形最早由前苏联学者提出,通过实测获得经过一定运转时间后的蜗杆分度环面上的磨损量曲线,即所谓自然修形曲线[7].进而采用抛物线对自然修形曲线进行拟合,实现抛物线修形.由于抛物线修形在本质上属于变工艺传动比修形,在数控装置普及之前,在生产实践中实现,有一定困难,因之曾采用变参数修形予以替代[8].
为了提高自然修形曲线的拟合精度,80 年代曾有学者提出高次方修形.在自然修形的研究过程中,长期没有获得加工修形蜗杆的工艺传动比的明确计算式,后来得到该计算式后,也没有在啮合分析计算的过程中,始终把工艺传动比当作变量处理,造成啮合分析的结果不能准确反映蜗杆副的实际工作状况[9].作为自然修形的一个变种,曲率修形通过建立修形量微分与蜗杆齿面曲率半径微分间的关系,修正蜗杆齿厚达到修形目的[10].
随着啮合理论的发展,诞生了理性修形.其基本原理是,在加工蜗杆或相应滚刀的过程中,蜗杆毛坯与刀座的相对位置及相对运动,和蜗杆副啮合过程中,蜗杆蜗轮的相对位置及相对运动,存在人为设置的差异,实现修形,达到去除常接触线扩大共轭区的目的.由于上述差异可以人为设置,意味着理性修形中,工艺传动比可以取常值,从而降低理性修形实现的难度.
理性修形中,可调参数较多,诸如:工艺中心距、工艺传动比、刀座垂直高度、以及刀座轴线偏转角度等等,从而形成各色修形传动.不过,按照啮合特点,这些修形传动可以划分为:Ⅰ型传动、Ⅱ型传动和角修形传动等有限的类型.理论研究表明,综合施加不同参数修形,才能获得啮合性能较为优越的传动副.
本文基于自然修形数据,对其无量纲化处理后,用高次多项式拟合得到具有普适性的高次修形曲线,推导了修形曲线与工艺传动比i1d的关系式.根据微分几何及齿轮啮合理论系统地建立了具有变工艺传动比直廓环面蜗杆副的数学模型,证明了蜗杆螺旋面是不可展直纹面.并通过相关算例分析了高次方自然修形直廓环面蜗杆的局部啮合性能.
1 加工蜗杆工艺传动比的计算原理
1.1 高次方修形曲线
高次方修形曲线的优劣直接影响到蜗杆副的啮合性能,既有文献中的修形曲线是在特定参数下得到的.为扩充修形曲线的适用范围,进一步提高拟合精度,需建立普适型修形曲线.
在精车蜗杆螺旋面的过程中,蜗杆绕其轴线的转角为φ,车刀的所谓标称角度是φx,它们的几何关系如图1所示.据此可以把φx表示为
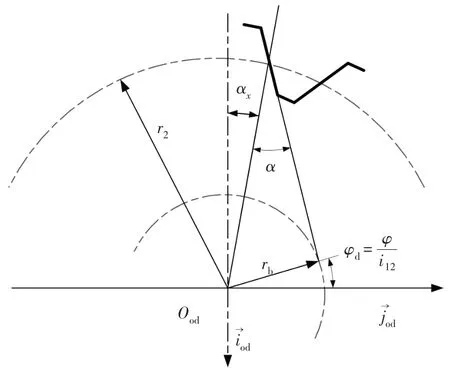
图1 蜗杆转角φ与标称角度φx的关系Fig.1 Relationship between worm angle φ and nominal angle φx

式中,α是蜗杆分度环面压力角.
文献[9]中对中心距a=500 mm、传动比i12=8的蜗杆副,按不同的标称角度φx,实际测量修形量,共获得i=35 组数据().建立修形曲线前,先对所得的数据无量纲化处理.为此首先定义转角系数

式中,φw为蜗杆包围蜗轮工作半角.
同样定义修形量系数Ii=,根据文献[8],不同中心距、传动比条件下蜗杆啮入端修形量Δf/mm可按下式计算

其中,a为蜗杆副标称中心距;式中10.25≤i12≤59.
文献[9]中的数据,经上述方法处理后,得到的无量纲化的修形数据列于表1.
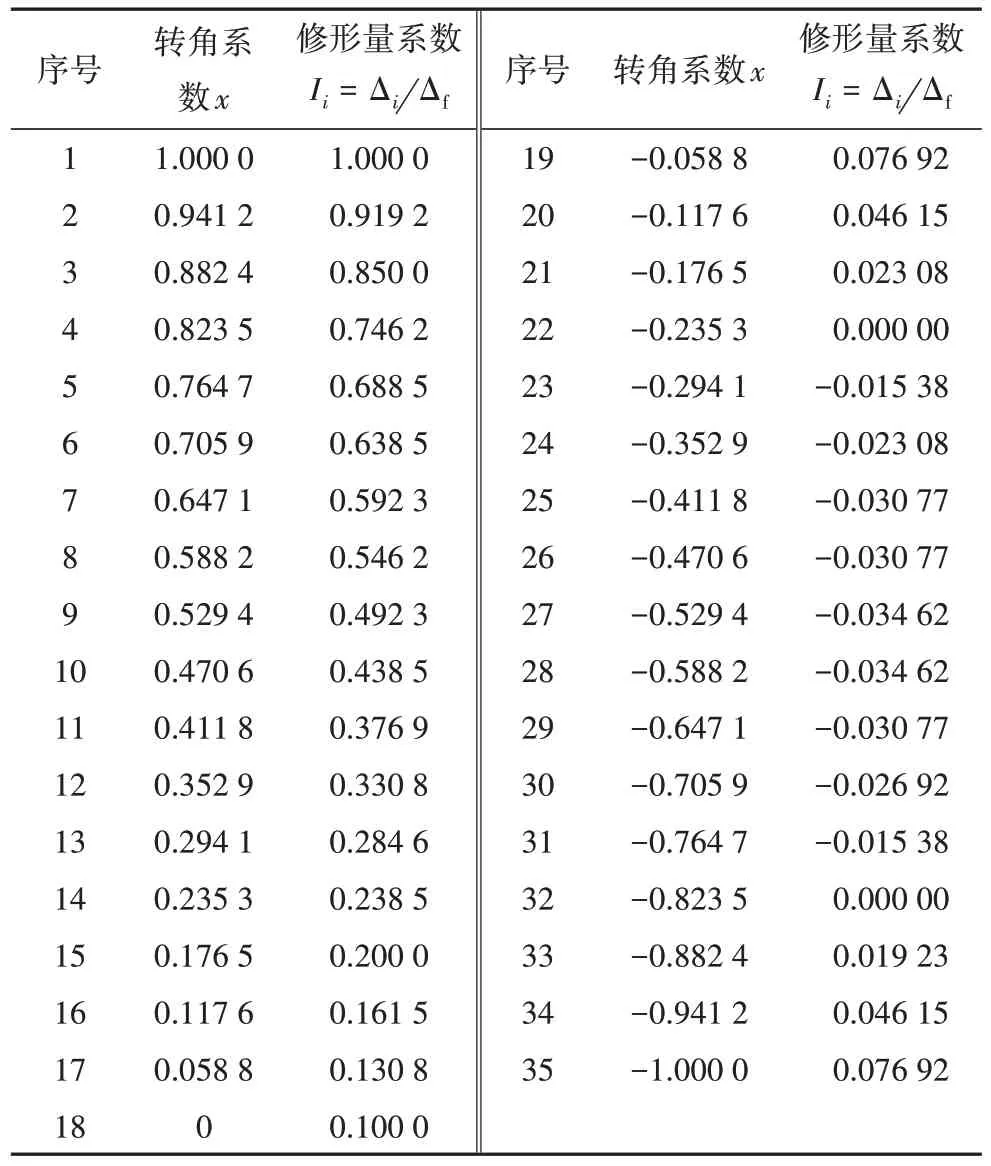
表1 无量纲化修形数据结果Tab.1 The result of dimensionless modification data
对上述修形数据以最小二乘法拟合得到修形量系数的函数为

对式中多项式幂次n取不同数值,可得到式中不同次多项式的系数ck,将计算的数值结果列于表2.

表2 各次修形曲线多项式系数Tab.2 Polynomial coefficients of various modification curves
以3 次修形量系数的函数为例,拟合得到的曲线图像如图2.x=-1,x=0,x=1 分别对应蜗杆副的啮出端、喉部和啮入端.
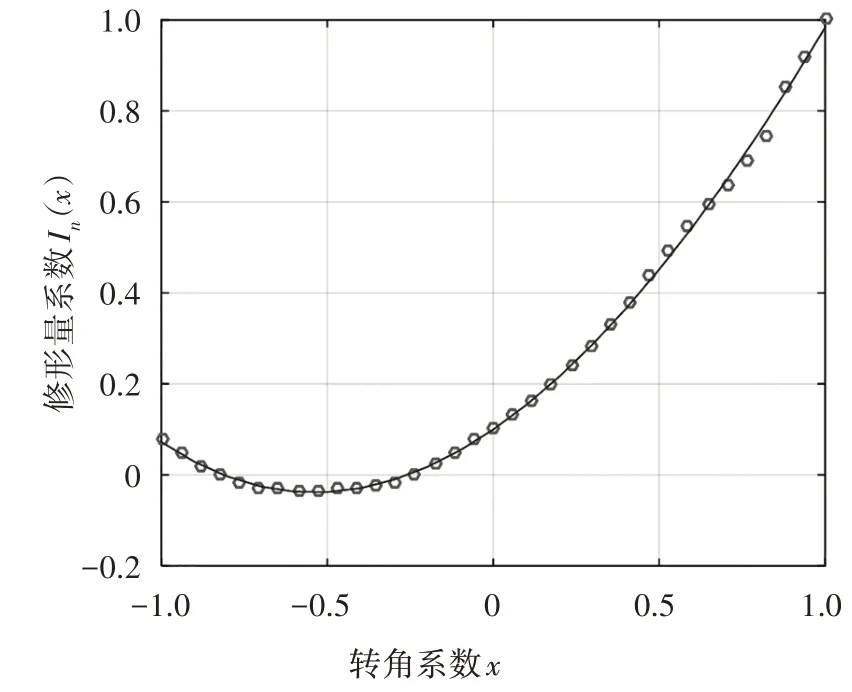
图2 3次修形量系数的函数曲线Fig.2 The curve of the coefficient of the cubic modification amount
由式(4)和表2 中的数据得到修形曲线函数表达式为
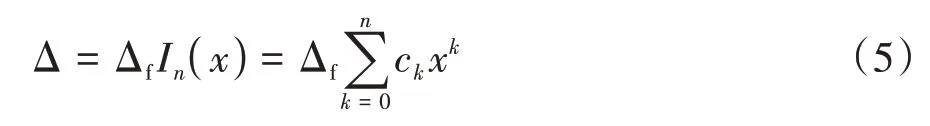
当多项式幂次n=2 时,式(5)为抛物线修形曲线函数;当n>2,即为高次方修形曲线函数.
通过提高拟合多项式的次数n,可以提升式(4)的拟合精度.为此基于表1 中数据计算各次曲线的误差,其结果如表3所示.
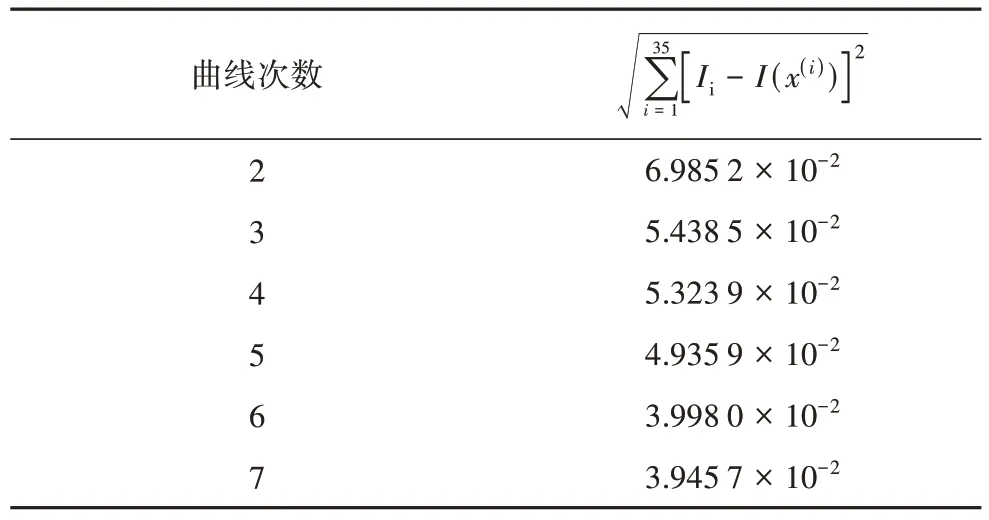
表3 各次曲线的总误差Tab.3 Total error of various curves
由表3 可知,单纯提高拟合多项式的次数,并不能显著提升拟合精度.
1.2 工艺传动比与修形曲线函数的关系
由图1 可建立加工蜗杆毛坯时刀具的附加转动Δφd与修形量变化的关系式

式中,r2为蜗轮分度圆环半径.
因此,加工修正型直廓环面蜗杆时刀具转角为
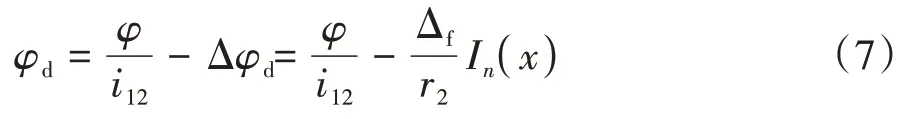
任意转角下刀座与蜗杆的传动比为
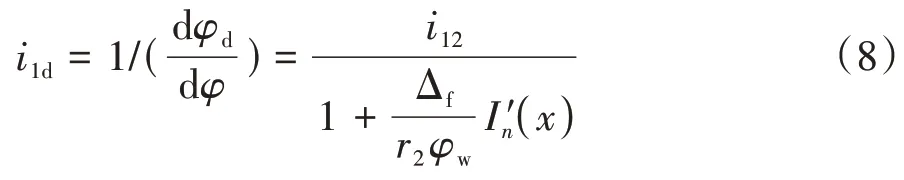
在式中,啮入端修形量Δf、蜗轮分度圆半径r2和工作半角φw均为常值且为正数.因此,工艺传动比i1d与公称传动比i12的大小关系由决定.在图2 中,为曲线的斜率,由此可知对应的转角系数在x=-0.5 左右,在x=-0.5附近右侧,>0,i1d<i12;在x=-0.5附近左侧<0,i1d>i12.
2 高次方修形蜗杆传动啮合理论
2.1 坐标系的选取及直线刀刃方程
如图3,直廓环面蜗杆的齿面是由直线刃车刀加工而成,与蜗杆相配对的蜗轮是由与蜗杆形状相同的滚刀加工而成.

图3 直廓环面蜗杆成型原理Fig.3 The forming principle of straight profile toroidal worm
图3中u为直线刃车刀参数,由此可得刀刃直线方程

根据蜗杆副加工啮合原理,可确定各坐标系的位置关系,建立如图4坐标系系统.

图4 坐标系的位置关系Fig.4 The positional relationship of the coordinate system
对式(9)做旋转矩阵变换得到σod中刀刃直线族方程为

式中:xod=-ucosφd-rbsinφd,yod=-usinφd+rbcosφd,为绕旋转的矢量矩阵[11].进而由式(10)求得σ1中蜗杆螺旋面方程
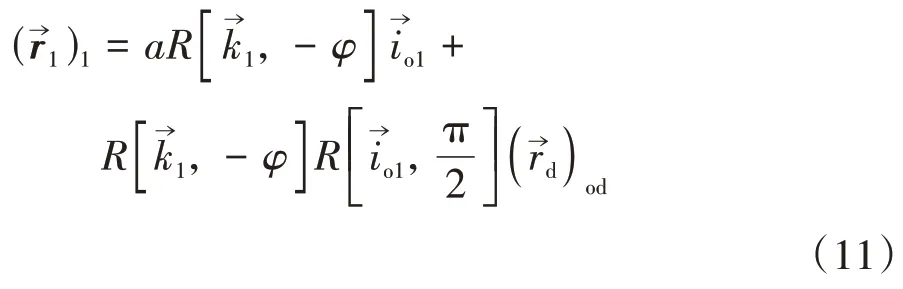
2.2 直廓环面蜗杆螺旋面不可展性的数学证明
σ1中蜗杆的螺旋面方程也可以写成以下形式

其中
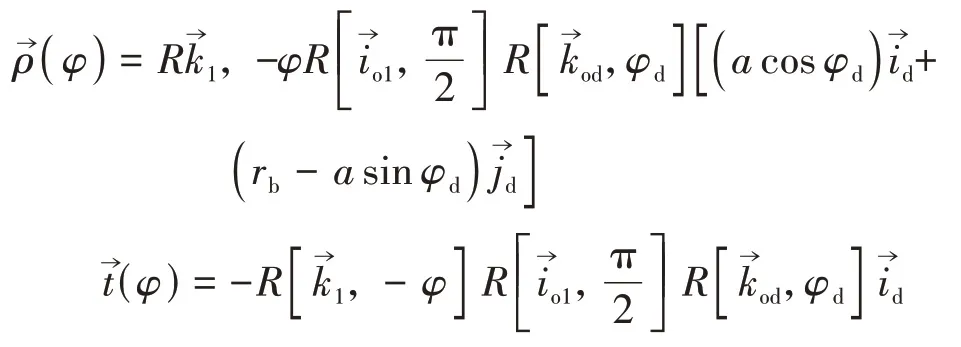
式(12)与直纹面的标准方程相符.在此基础上证明其不可展.从式(12)计算导矢,分别令对φ求导
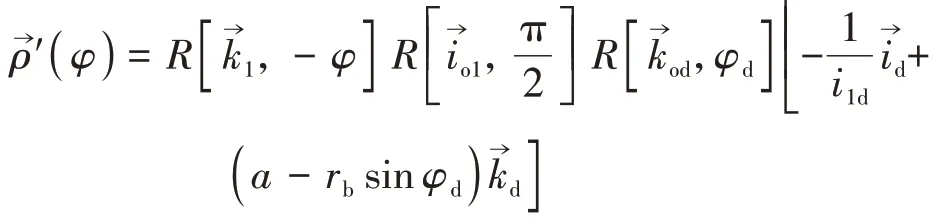
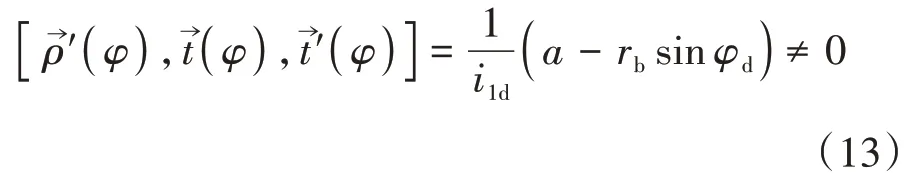
这与可展曲面的判定条件相悖,即直廓环面蜗杆的螺旋面为不可展.综上可得,直廓环面蜗杆的螺旋面为不可展的直纹面.
2.3 蜗杆螺旋面的两类基本量及曲率参数
由式(11)可得u、φ两个方向偏导矢
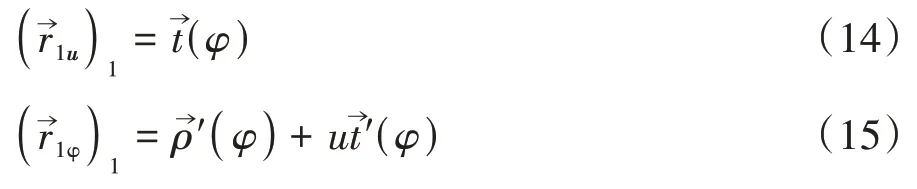
根据微分几何理论求得直廓环面蜗杆螺旋面的第一类基本量为
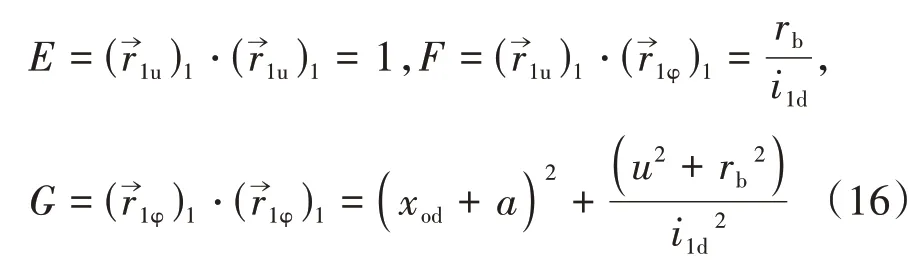
由式(14)(15)及第一类基本量求得坐标系σ1中蜗杆的螺旋面单位法向量为
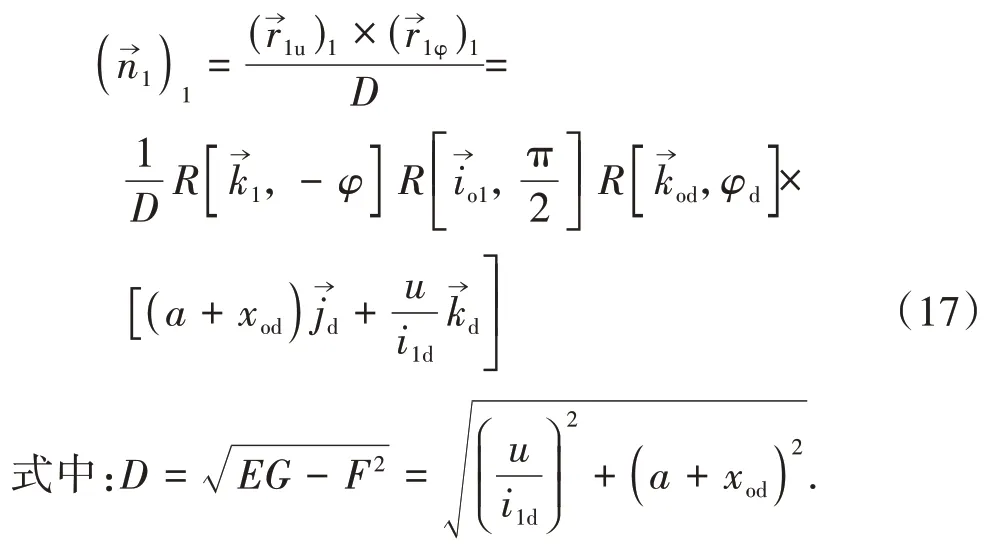
为计算螺旋面的第二类基本量,分别计算蜗杆螺旋面方程对u、φ的二阶偏导矢

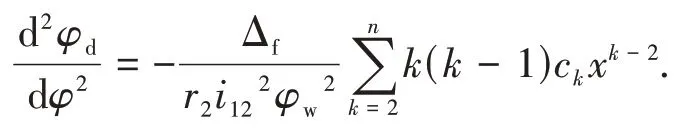
从式(17)(18)(19)和(20),可以计算出直廓环面蜗杆螺旋面的第二类基本量如下:
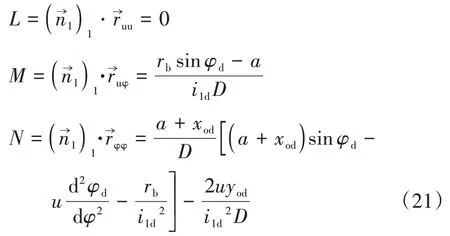
沿u方向的单位切向量和正交于的单位切矢量可表示为[12]
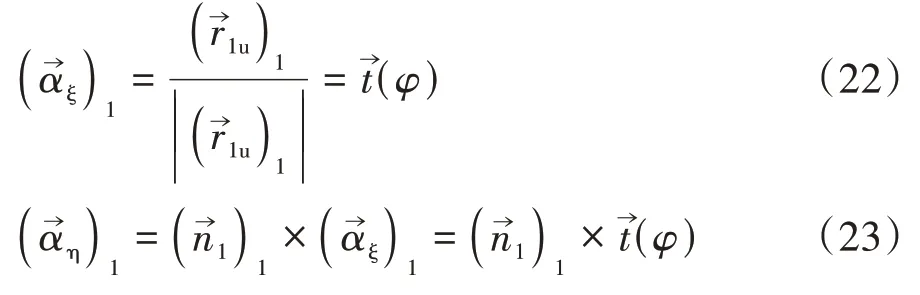
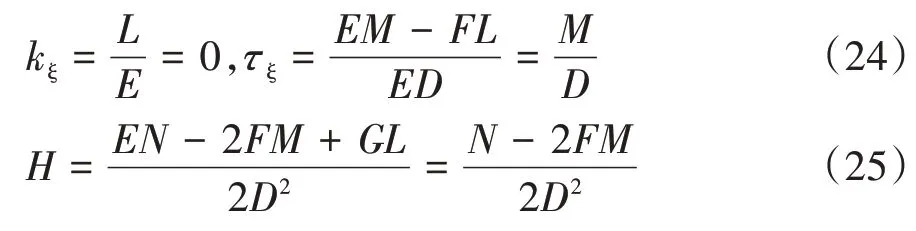
2.4 蜗轮的齿面方程及啮合函数

由旋转变换得到σo1中蜗轮齿面生成面族方程

同理蜗轮齿面生成面族的单位法向量也可由旋转矩阵变换得到
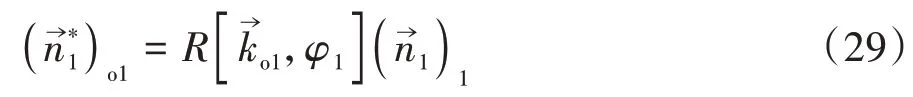
在σo1中蜗杆螺旋面和蜗轮齿面啮合的相对速度矢量为
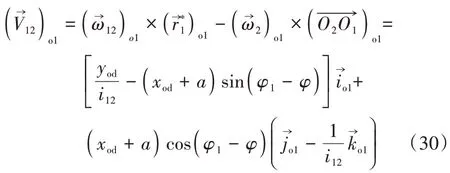
σo1中两个单位切向量为
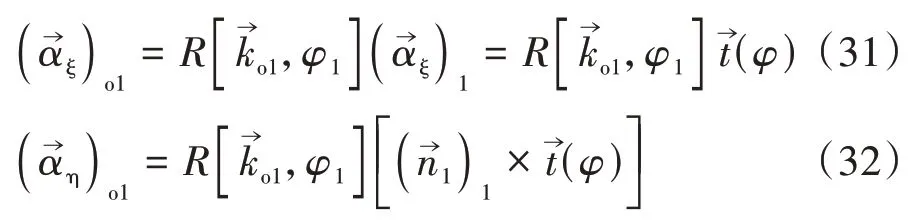
由式(29)和式(30)推导啮合函数如下[13-15]:
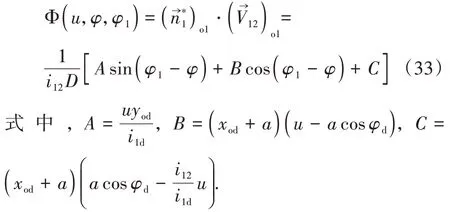
由蜗杆副满足关系Φ(u,φ,φ1)=0可得
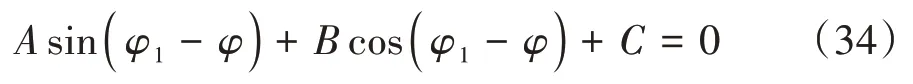
对式(34)进行三角变换
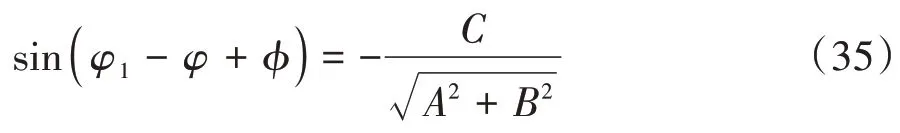
式中φ满足以下关系:

由式(35)得到一个啮合周期内φ1的两个解:
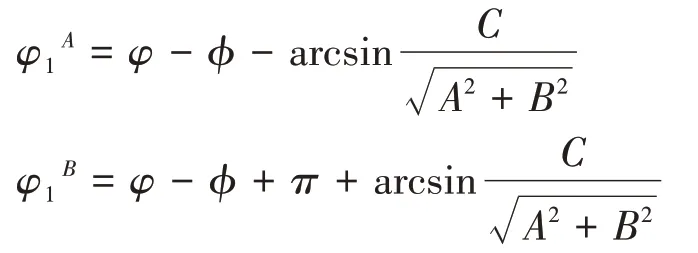
这两个解分别表示在子共轭区ΣA和ΣB中φ1与u、φ的关系.在σ2中蜗轮齿面两个子共轭区ΣA和ΣB的方程分别为
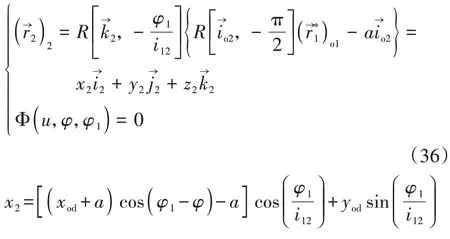
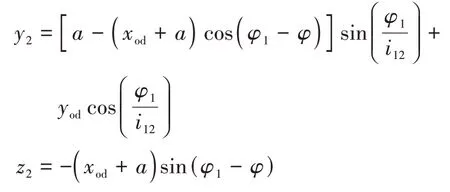
由式(33)对φ1微分得到直廓环面蜗杆副的啮合极限函数为

直廓环面蜗杆啮合过程中的瞬时接触线的法向量为

各项因式乘积的计算结果表示如下:
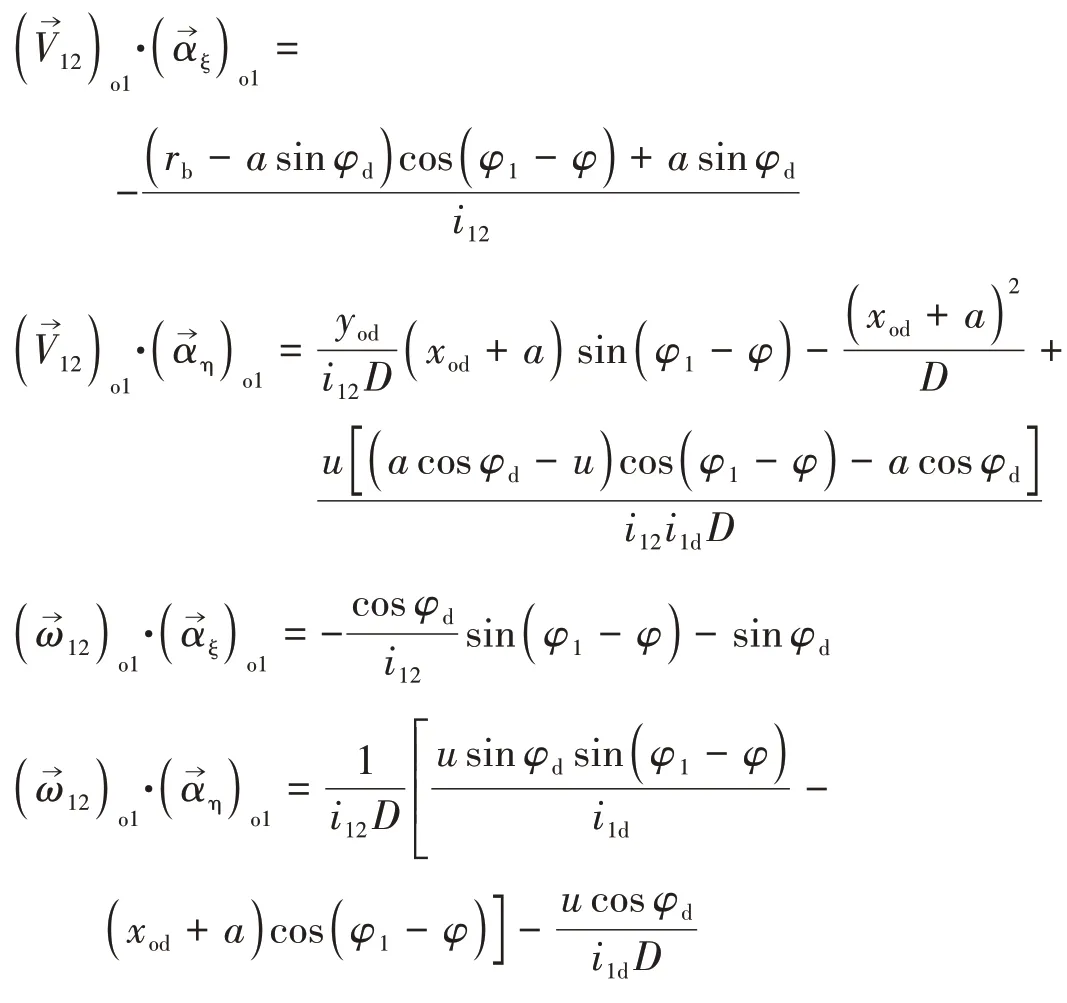
据式(37)(38)可求得曲率干涉界限函数为
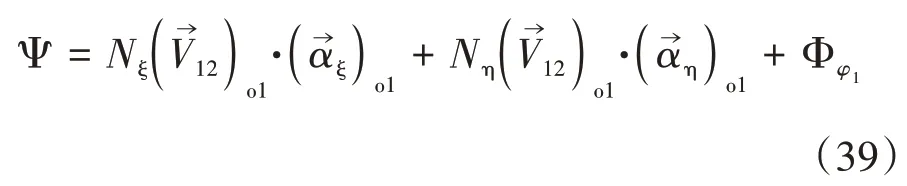

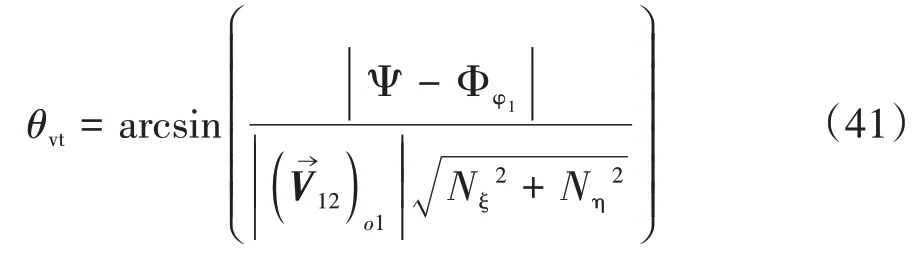
3 数值算例分析
仿真分析部分采用数值算例的蜗杆副参数为Z1=2,a=280 mm,i12=25.表4 中给出了算例所需参数的计算方法及其数值结果[16-17].

表4 蜗杆副参数Tab.4 Worm pair parameters
3.1 原始型直廓环面蜗杆传动的啮合特性
图5 基于蜗杆传动啮合理论,令i1d=i12可以得到无修形的原始型传动.按表4 中的技术参数,绘出了原始型传动的共轭区与接触线.

图5 原始型直廓环面蜗杆啮合特性Fig.5 Meshing characteristics of primitive straight profile toroidal worm
图5(a)为蜗杆螺旋面在{O1;yo1,zo1}平面上的投影.区域ABCD为传动副的共轭区ΣA,由式(34)可知,此区域内φ1=φ,AB线和CD线分别代表蜗杆的啮入端与啮出端.
图5(b)为蜗轮齿面在{O2;z2,RB}平面上的投影,纵坐标RB=.AB线、CD线以及接触线1-5重合,此区域退化为常接触线.区域A*B*FE为传动副的新接触区ΣB.蜗杆螺旋面上的A*B*线代表共轭区ΣB的啮入端,EF线为传动副的曲率干涉界线,沿此线Ψ=0.同时EF线是共轭区ΣA与ΣB的公共边界,构成传动副啮合界线,沿此线=0.因此在蜗轮齿面上EF线不起曲率干涉界线的作用,不引起曲率干涉,只对在蜗杆齿面上共轭区ΣB起啮合界线的作用.沿EF线传动副瞬时接触线法矢量=0,因此它是瞬时接触线的奇点轨迹.
分别在瞬时接触线与蜗轮齿顶、蜗杆分度圆和蜗杆齿顶交点处选取3 个采样点,计算采样点诱导法曲率和滑动角θvt的数值结果列于表5中.数据表明,在整个ΣB区上,的值较小,即齿间的接触应力小,油膜厚度相应增大[18].且该子共轭区的θvt值较大,尤其在EF线附近数值接近90°,表明形成油膜的条件良好.
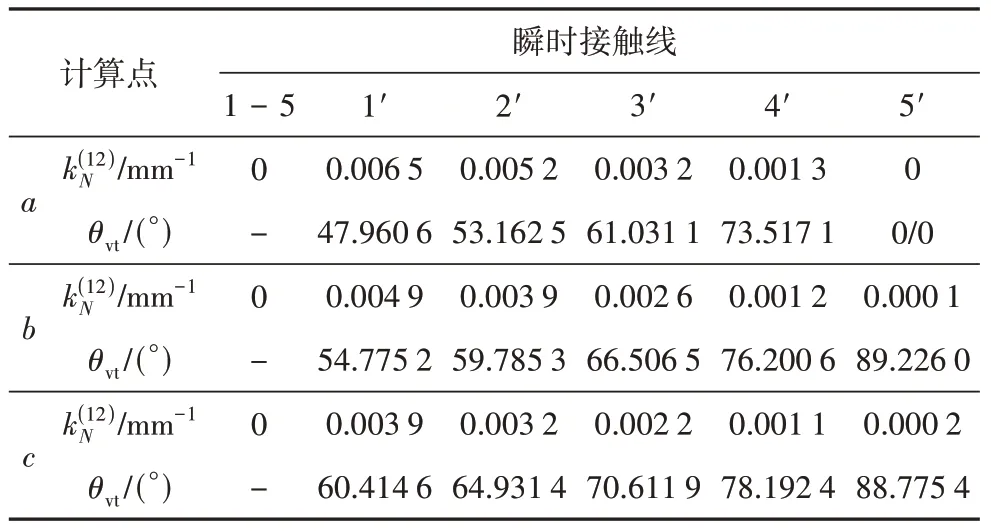
表5 原始型直廓环面蜗杆啮合质量Tab.5 Meshing quality of original globoidal worm drive
3.2 高次方修形直廓环面蜗杆传动的啮合特性
为了防止过于繁冗,文中只给出3次、5次和7次曲线修形直廓环面蜗杆副的算例分析,如图6-7 和图8所示.
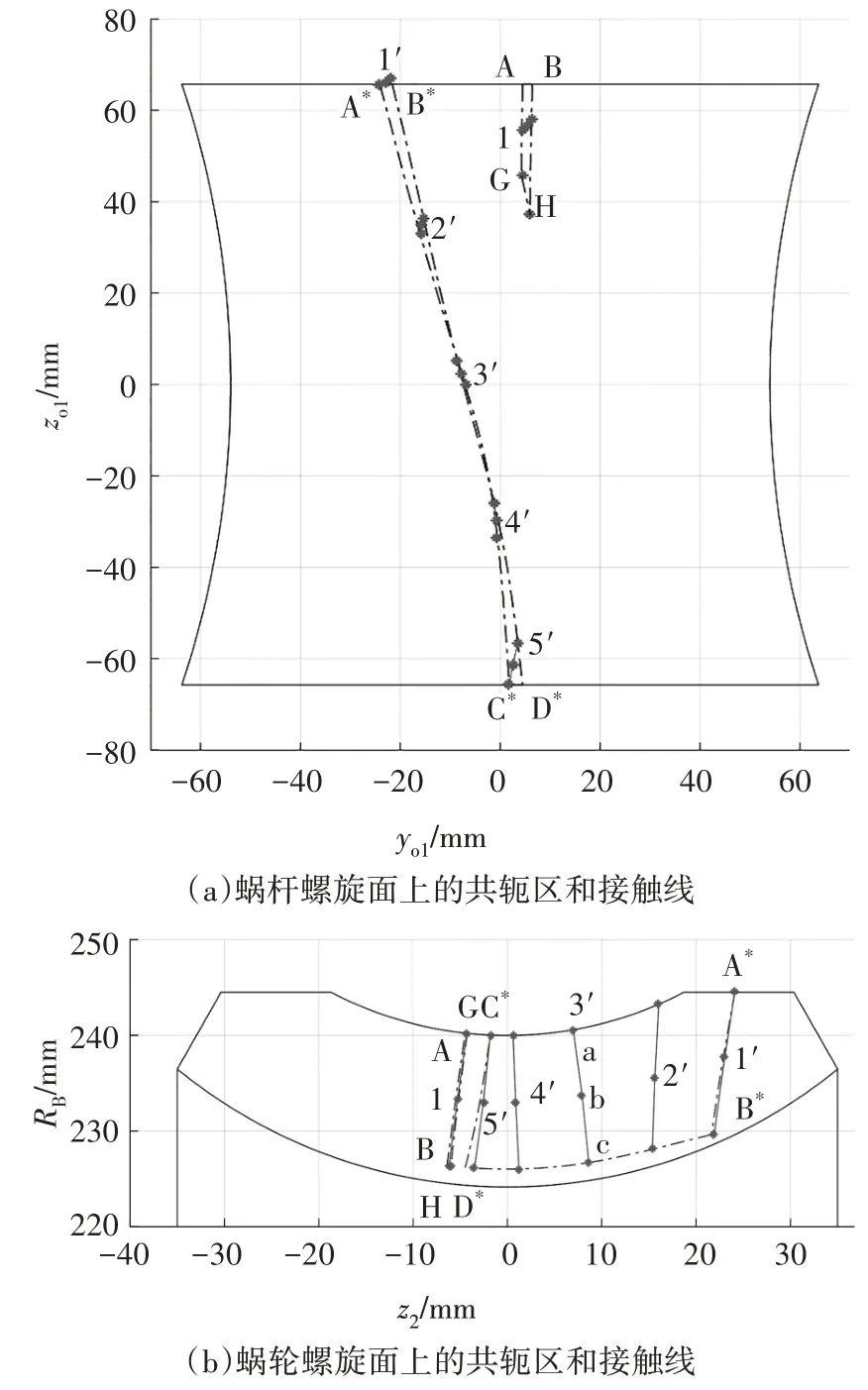
图6 3次曲线修形后蜗杆副啮合特性Fig.6 The meshing characteristics of the worm pair after cubic curve modification
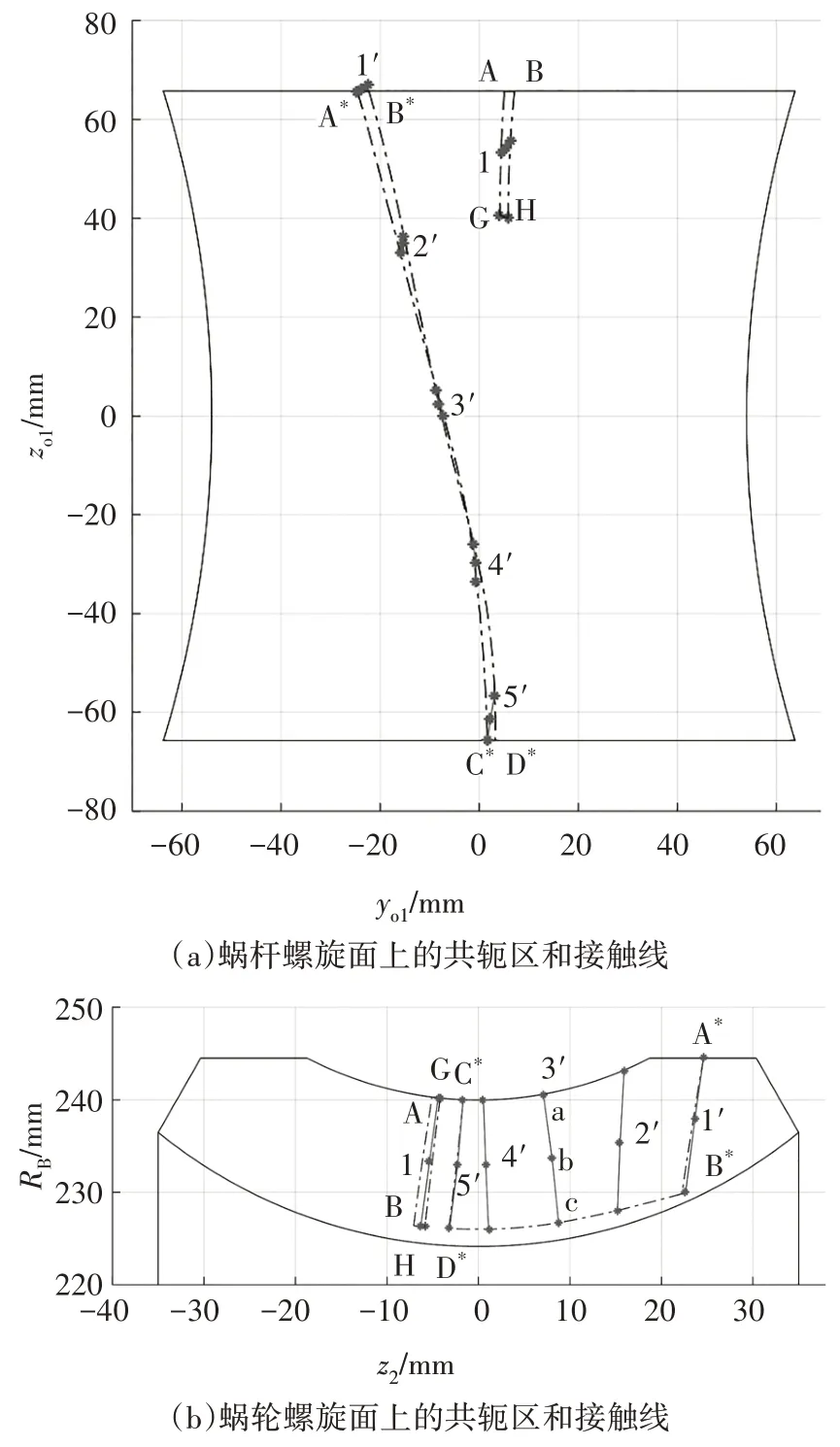
图7 5次曲线修形后蜗杆副啮合特性Fig.7 The meshing characteristics of the worm pair after the fifth power curve modification
图6(a)和图7(a)中,区域ABHG为子共轭区ΣA,相比于原始型直廓环面蜗杆副,ΣA区不再退化为常接触线.但区域内存在曲率干涉界线GH,ΣA区不能贯彻蜗杆螺旋面的始终.区域A*B*D*C*为子共轭区ΣB,区域内的啮合界线被消除,子共轭区ΣB扩大至蜗杆的啮出端,C*D*线为啮出端的反映线.这表明,修形后的蜗杆仍为全长可用,且在啮入端附近实现部分双线传动.
图6(b)和图7(b)中,蜗轮齿面上的子共轭区ΣA和ΣB均增大.且与3 次修形相比,5 次修形的ΣA区更大一些.
表6和表7中,ΣA区的诱导法曲率值较小,滑动角θvt值较大,啮合性能良好.相比于原始型直廓环面蜗杆,修形后ΣB区中的诱导法曲率并无明显变化,滑动角θvt值略微增大,油膜的形成条件更良好.在曲率干涉界线GH上Ψ=0,诱导主曲率无限大,接触应力也无限大,导致蜗杆副失效.
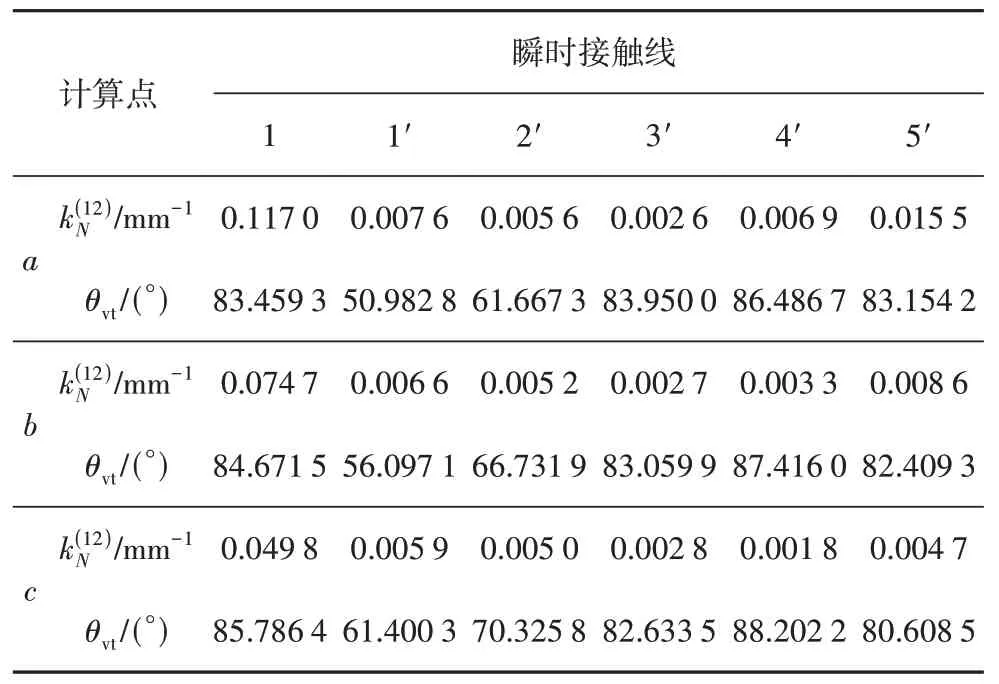
表6 3次修形直廓环面蜗杆啮合质量Tab.6 Meshing quality of cubic curve modified globoidal worm drive
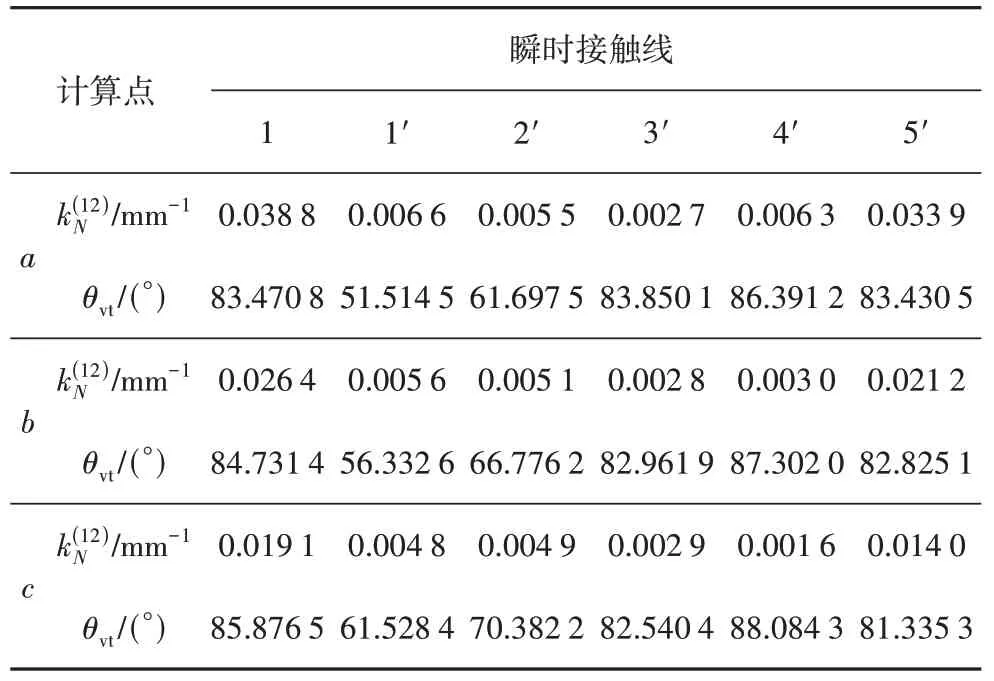
表7 5次修形直廓环面蜗杆啮合质量Tab.7 Meshing quality of fifth power curve modified globoidal worm drive
提高修形曲线的拟合幂次后,子共轭区ΣA面积可以明显增大,如图8 所示,ΣB区的啮出端反映线C*D*部分进入ΣA区.D*点的蜗杆转角=1 357.7°,曲率干涉界线GH与蜗杆齿顶环面交点H的蜗杆转角=286.19°.由于,说明ΣB区的蜗杆啮出端反映线C*D*,在曲率干涉界线GH之后进入了共轭区ΣA,因此可以将其D*NH区域切除,也就是切除了曲率干涉界线GH靠近蜗轮齿根的部分NH.N点为蜗轮齿面上曲率干涉界线GH和C*D*线的交点,可通过求解由曲率干涉界线函数Ψ=0、蜗杆啮出端边界条件、以及ΣA和ΣB中N点在坐标系{O2;z2,RB}中横纵坐标分别相等构成的方程组确定[19].在蜗杆螺旋面上,D*N线是啮出端在共轭区ΣA内的反映线,如图8(a)所示.
位于该区上的瞬时接触线1 是根据A点到G点蜗杆转角的中间值得到的,其明显更靠近边界MNG,这说明ΣA区内瞬时接触线分布不均匀,在边界MNG附近瞬时接触线更密集,在蜗杆副的传动过程中接触频率更高,容易发生点蚀.
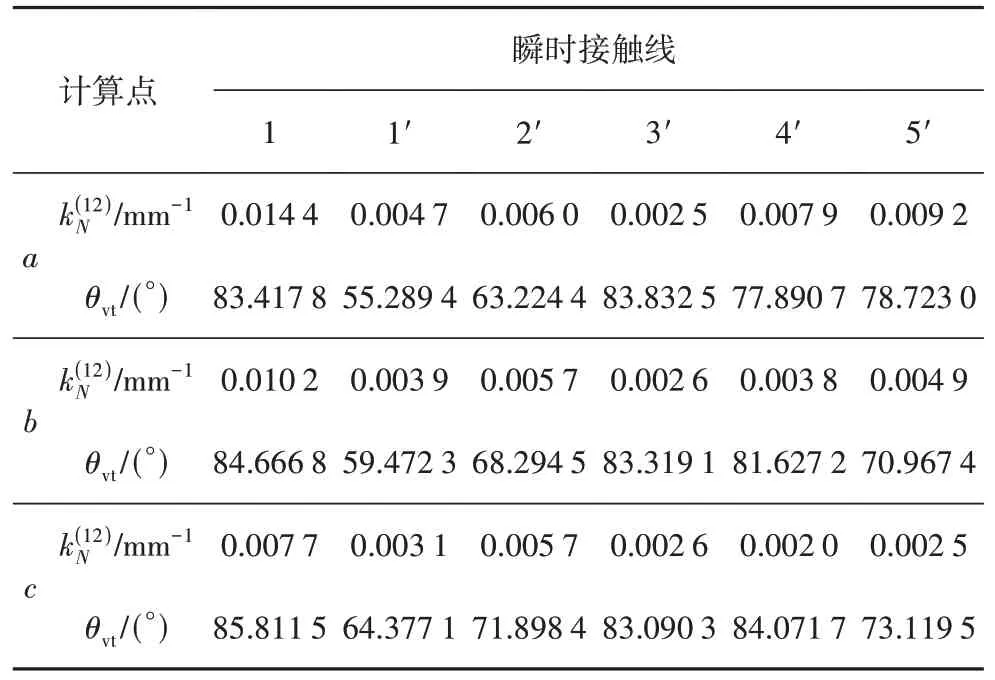
表8 7次修形直廓环面蜗杆啮合质量Tab.8 Meshing quality of seventh power curve modified globoidal worm drive
4 结论
通过对修形数据无量纲化处理,推导出了更具普适性的高次方修形曲线函数,在此基础上获得了加工直廓环面蜗杆螺旋面的工艺传动比的计算式.从而通过工艺传动比,把修形曲线的影响引入啮合分析的计算,改变了既有文献中只考虑修形曲线对蜗杆齿厚影响的旧观念.在这个意义上,基于修形曲线的修形应属于变传动比修形,工艺传动比在本质上是时间的函数.数值结果表明,单纯提高修形曲线函数的幂次,对于提升修形曲线拟合精度的作用是十分有限的.
基于旋转变换矩阵,全面建立了高次方修正型直廓环面蜗杆传动的啮合理论,通过所得到的工艺传动比公式,精确地考虑了修形曲线的影响,弥补了先前文献在这方面的不足,严格论证了其蜗杆螺旋面为不可展的直纹面.
数值计算结果表明,高次方修形可以去除蜗轮齿面的常接触线,并扩大接触区,同时使蜗杆全长参与啮合,且在入口部分保持一定长度的双线接触.高次方修形对诱导主曲率及滑动角等局部啮合性能指标影响不大.主要不足之处是,蜗轮齿面中部靠近齿顶部位存在一定程度的曲率干涉,提升修形曲线函数的幂次,可以消减蜗轮齿面上曲率干涉界线的长度,但难以将其去除净尽.
综合考量,高次方修形需按一定规律改变加工蜗杆的工艺传动比,在工艺方面相对比较复杂,又存在一定程度的曲率干涉,因此不宜单独采用.
