四轮驱动EV 自适应抗差无迹粒子滤波状态估计
2022-02-27龙云泽韦韬封进张瑞宾
龙云泽,韦韬,封进,张瑞宾
(桂林航天工业学院汽车工程学院,广西桂林 541004)
四轮驱动电动汽车(Electric Vehicle,EV)省去了传统燃油车较长的传动链,具有车辆底盘结构简单、传动效率高、驱动形式多样化等优点,已成为全球汽车领域研究热点[1].四轮驱动EV 的轮毂电机驱动力独立可控,可实现整车多动力学状态驱动,而整车状态参数值的精确性是影响驱动模式优化及主动安全控制的关键因素.
近年来,改进卡尔曼滤波算法在四轮毂电机汽车整车状态估计中得到了广泛的运用[2].扩展卡尔曼滤波(extended Kalman filter,EKF)理论可实现整车非线性系统的状态估计,但此方法需要计算复杂的雅可比矩阵,且存在线性化误差的影响[3-4].无迹卡尔曼滤波(unscented Kalman filter,UKF)引入无损变换的思想,有效地克服EKF估计精度低、稳定性差的问题,在四轮驱动汽车状态估计中得到了较好的应用,但其对整车参数估计结果在系统强非线性状态下,精度会下降明显[5].粒子滤波(particle filter,PF)的思想是利用粒子集来表示概率,从后验概率中抽取的随机状态粒子来表达其分布,该滤波方法具有较强的非线性适应能力及多模态处理能力.但该方法在重采样阶段会造成样本有效性和多样性的损失,导致样本贫化现象.国内外不少学者运用粒子群优化粒子滤波算法实现整车状态估计,取得较好效果,但算法存在计算量较大,工程实现困难大的问题[6-8].无迹粒子滤波(unscented particle filter,UPF)算法运用无迹卡尔曼滤波方法生成建议密度函数,使先验概率峰值与似然函数峰值具有良好的吻合性,达到降低粒子退化的目的,但其运算精度受系统噪声不确定性的影响,且缺少自适应调整机制,不能对滤波增益及相关参数进行实时调节.
抗差估计滤波方法,可对滤波器参数进行实时调节,对干扰噪声具有较好的自适应性[9].基于抗差滤波原理及无迹粒子滤波算法,构建自适应抗差无迹粒子滤波算法(adaptive robust unscented particle filter,ARUPF),通过整车动力学模型理论预测与实际测量融合的方法,实现四轮驱动电动汽车状态的精确估计.为解决四轮驱动电动汽车状态估计问题,建立整车七自由度整车动力学模型,通过引入权矩阵及自适应调节因子构建自适应抗差无迹粒子滤波算法,实现对整车状态的精确估计,并运用CarSim 与Matlab/Simulink 软件进行联合仿真验证该方法的有效性.
1 四轮驱动电动汽车动力学建模
从七自由度整车动力学模型、车轮运动学模型、轮胎模型三个方面搭建四轮驱动汽车动力学模型.通过魔术公式轮胎模型计算各轮胎纵向及侧向驱动力,并结合七自由度整车动力学模型与车轮运动学模型进行整车动力学状态分析[10].
1.1 七自由度整车动力学模型
建立四轮毂电机驱动车七自由度动力学模型,如图1 所示.研究的目标为对整车行驶过程中纵向速度、侧向速度、质心侧偏角进行实时准确估计.因此模型考虑整车纵向运动、侧向运动、横摆运动及四轮毂电机转动自由度.模型作了以下近似:1)忽略整车垂向运动、绕y轴的俯仰运动、绕x轴侧倾3个运动的影响;2)忽略滚动阻力影响;3)忽略风阻影响;4)假设两前轮具有相同的转向角和侧偏角;5)采用传统的前轮转向方式;6)假设两后轮的侧偏角一致;7)假设各轮胎动力学特性一致.七自由度四轮毂驱动汽车动力学方程如下[11-12].


式中;vx为整车纵向速度;vy为整车侧向速度;γ为整车横摆角速度;ax为纵向加速度;ay为侧向加速度;Fxfl、Fxfr、Fyfl、Fyfr、Fxrl、Fxrr、Fyrl、Fyrr分别为左前轮纵向力、右前轮纵向力、左前轮侧向力、右前轮侧向力、左后轮纵向力、右后轮纵向力、左后轮侧向力、右后轮侧向力;M为横摆力矩;β为质心侧偏角;δf为前轮转向角;m为整车质量;df、dr分别为前、后轮轮距.αfl、αfr、αrl、αrr分别为左前轮、右前轮、左后轮、右后轮轮胎侧偏角.
1.2 车轮运动学模型
四轮驱动电动汽车车轮运动学模型为:
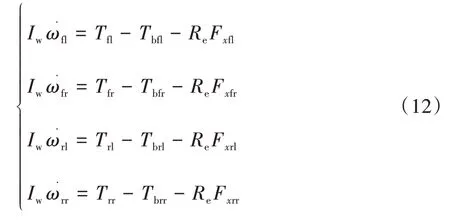
式中:Iw为车轮转动惯量;ωfl、ωfr、ωrl、ωrr分别为左前轮、右前轮、左后轮、右后轮转动角速度;Tfl、Tfr、Trl、Trr分别为左前轮、右前轮、左后轮、右后轮驱动转矩;Tbfl、Tbfr、Tbrl、Tbrr分别为左前轮、右前轮、左后轮、右后轮制动转矩;Re为车轮滚动半径.
1.3 魔术公式轮胎模型
魔术公式轮胎模型能较好地模拟轮胎非线性动力学特性,得出各轮的纵向力与侧向力.魔术公式轮胎模型公式如下:
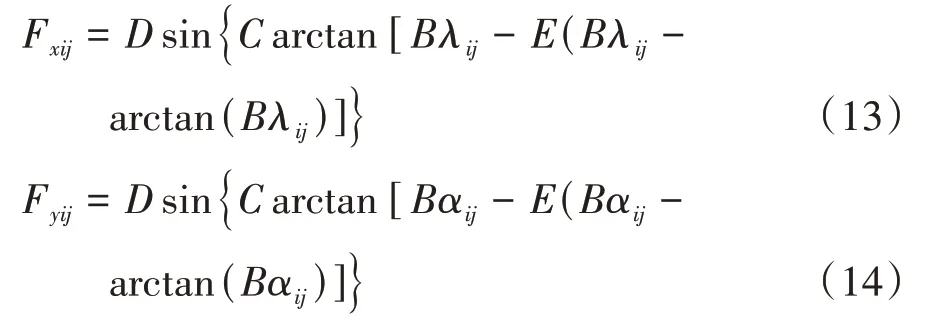
式中:Fxij为车轮纵向力;Fyij为车轮侧向力;B为刚度因子;C为曲线形状因子;D为峰值因子;E为曲线曲率因子;λij为纵向滑移率;αij为侧偏角.其中纵向滑移率λij分为驱动与制动两情况[13]:

式中:re为车轮有效滚动半径;ωij为车轮滚动角速度;vij为车轮中心运动速度.
2 ARUPF整车状态估计算法
以七自由度汽车动力学模型为基础,四轮驱动电动汽车行驶状态估计原理如图2 所示.基于ARUPF 算法,运用整车状态预测值与传感器观测值相结合,实现对整车行驶状态的实时估计[14].
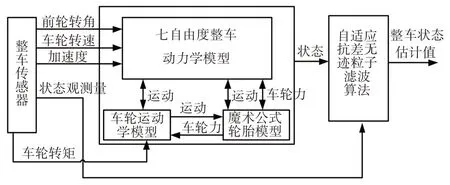
图2 整车行驶状态估计算法结构原理Fig.2 Structure and theory of vehicle driving state estimation algorithm
传统的粒子滤波算法存在迭代过程中粒子退化的缺陷,造成计算资源浪费、估计结果精度偏低等问题.为解决以上问题,常运用增加粒子数、重采样、选择合理的建议密度函数等方法对滤波算法进行优化.增加粒子数可有效缓解粒子退化,但增加了系统计算工作量.重采样方法可增加粒子的多样性,避免粒子退化.自适应抗差无迹粒子滤波算法利用无迹变换算法为每个粒子计算均值和协方差并建立合理建议密度函数,并结合抗差滤波估计算法自动调节增益矩阵及系统方差,使样本点分布较好地与最大似然函数吻合.无迹粒子滤波算法易于工程实现,能有效减少系统计算工作量,其具体方法如下:
1)初始化,k=0,从先验分布抽取初始状态粒子.
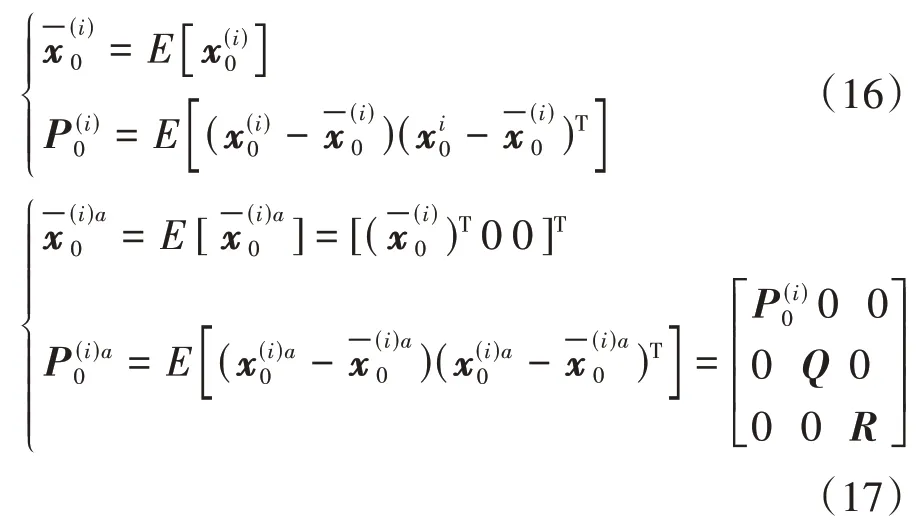
2)重要性采样.运用无迹卡尔曼算法计算均值与方差.
(1)抽取Sigma点集合.

(2)对Sigma点集进行一步预测.
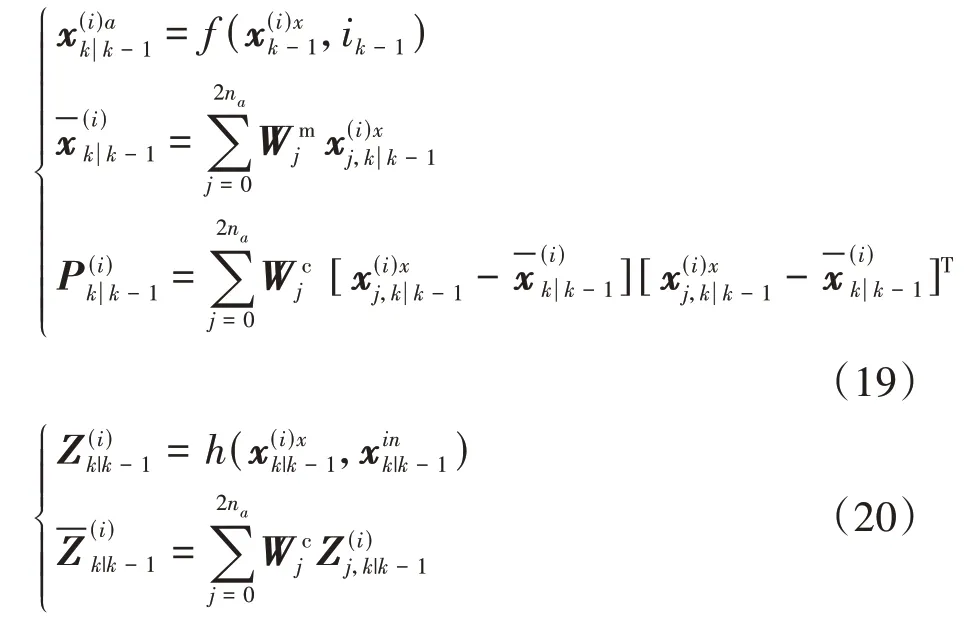
(3)融入观测数据,更新Sigma点集均值、卡尔曼增益及协方差.

3)ARUPF 算法.ARUPF 算法基于抗差估计滤波理论,对动力学模型观测量值异常情况加以控制,并构建自适应因子对动力学模型误差加以控制.设为状态向量的权矩阵,则等价权阵为.运用IGG(Institute of Geod⁃esy&Geophysics)方法产生等价权函数,其原理如下:
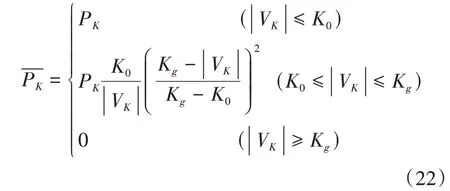
式中:Vk=为传感器探测残差值;调节因子参考取值范围K0∈(1,1.5);调节因子参考取值范围Kg∈(3,8).
令传感器感知矩阵为Ak,根据权矩阵,对系统状态向量进行更新.可得自适应抗差卡尔曼滤波的系统状态解向量为:
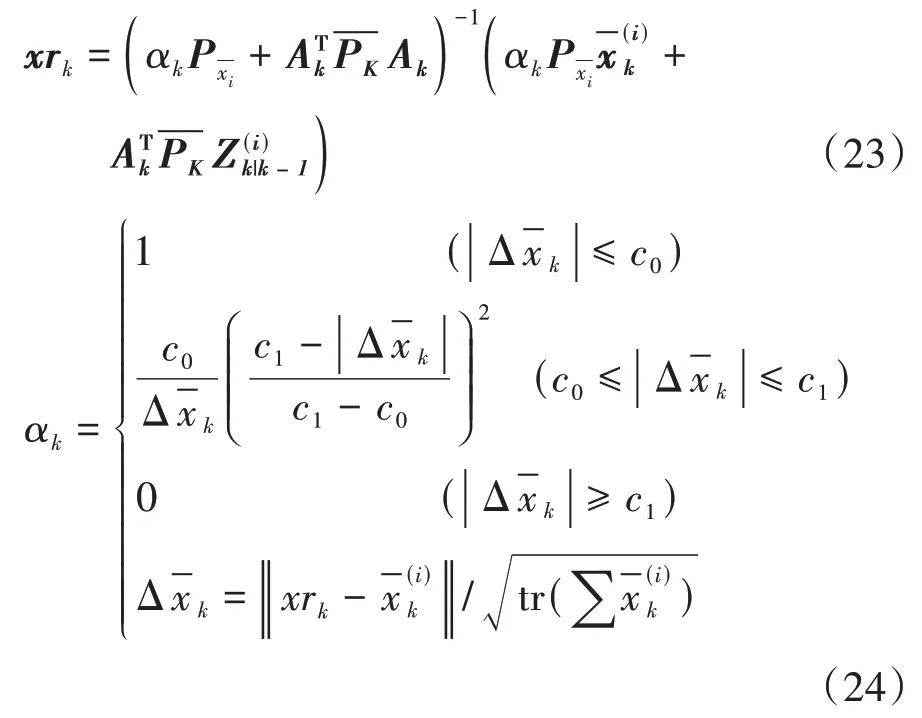
式中:αk为自适应因子;调节因子c0参考取值范围c0∈(1,1.5);调节因子c1参考取值范围c1∈(3,8);tr为矩阵求迹运算符.
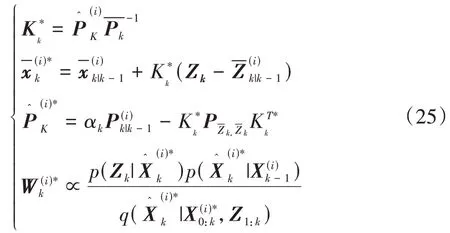
3 仿真实验验证
运用CarSim 与Matlab/Simulink 软件进行联合仿真实验对估计算法进行验证.CarSim 软件专门针对车辆动力学特性搭建出各种车型动力学仿真模型,其模型的仿真性能接近于实车,仿真结果被国际众多汽车制造商和零部件供应商所采用.在CarSim 软件中搭建四轮毂驱动电动汽车模型,将其部分运行参数作为整车传感器测量参数输入Simulink 仿真软件.在Simulink 软件中搭建车辆动力学模型及ARUPF 滤波算法,进行车辆运行状态估计,并将估计值与CarSim 软件车辆模型进行对比验证[15].整车关键参数如表1所示.

表1 整车动力学模型关键参数Tab.1 Key parameters of vehicle dynamics model
CarSim 整车模型选用B 型车,仿真实验工况选用ISO双移线实验工况,车速为30 km/h,路面附着系数为0.6.所搭建CarSim 与Matlab/Simulink 联合仿真模型如图3所示.

图3 联合仿真模型原理图Fig.3 Schematic diagram of joint simulation model
基于ARUPF 算法,选取所估计的状态向量为x=[vx vy β]T.以Carsim 整车模型部分参数,作为传感器所测得的车辆状态真实值,输入至Simulink 整车动力学模型,进行状态预测.Carsim 整车模型的前轮转角、车轮转速、纵向加速度、侧向加速度、横摆角速度如图4(a)~图4(e)所示.将预测值与观测状态加入随机噪声,共同输入ARUPF 滤波器进行状态估计.将粒子滤波、无迹粒子滤波与自适应抗差无迹粒子滤波后整车状态估值与理想值对比,所得结果如图5(a)~图5(c)所示.

图4 车辆传感器输入参数Fig.4 Input parameters of vehicle sensors
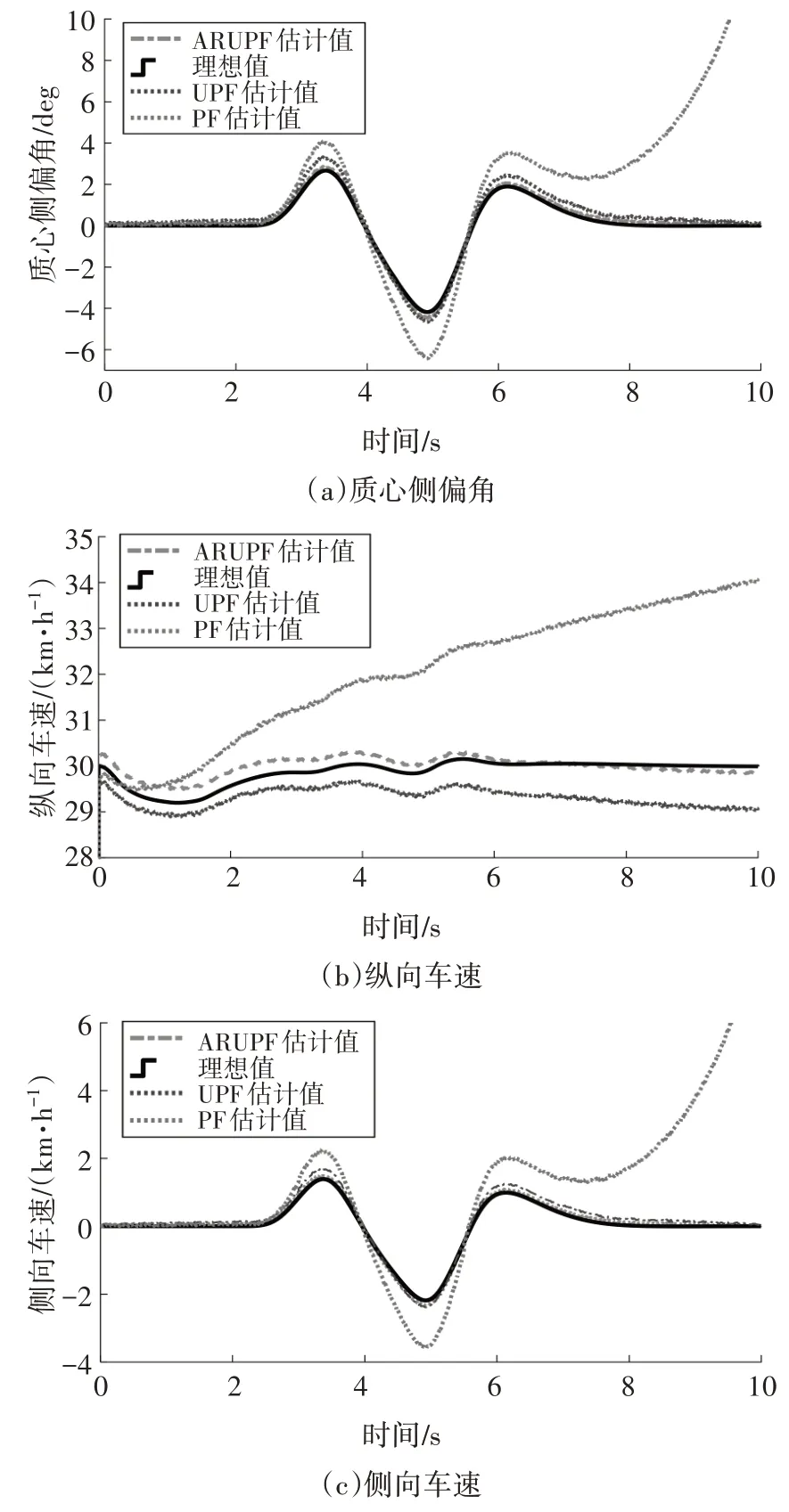
图5 基于ARUPF状态估计仿真结果Fig.5 Simulation results based on ARUPF state estimation
由仿真结果可知,CarSim 软件输出的真实值与Simulink 中所搭建仿真动力学模型的ARUPF 状态估计值相接近,验证了动力学模型的正确性.PF 估计值在后期由于粒子退化的原因易造成较大的估计误差,所采用ARUPF 状态估计算法有效地解决了传统粒子滤波算法样本贫化造成的精度下降问题,其状态估计的精度优于UPF 算法.所搭建ARUPF 滤波器针对过程噪声的滤波效果较好,具有较好的自适应性及抗干扰能力.
4 结论
1)基于四轮驱动汽车结构特征及魔术公式轮胎模型,建立了前轮转向的四轮分布式驱动电动汽车七自由度动力学模型.模型采用低成本传感参数作为输入量,实现对整车纵向车速、侧向车速及质心侧偏角的估计,具有实现成本低、工程易实现、抗干扰能力较强的优点.为四轮分布式驱动电动汽车状态估计提供了一种新的思路.
2)给出了一种采用等价权矩阵解决四轮分布式驱动汽车传感器数据粗大误差干扰问题的新方法.运用IGG 方法产生等价权函数,通过自适应调节权矩阵,可有效抑制车辆传感器检测过程中因非线性因素造成的随机误差,减小干扰造成的数据失真影响,提高了整车状态估计精度.
3)运用自适应抗差滤波原理,结合无迹粒子滤波算法,提出一种新的四轮驱动电动汽车整车的状态估计方法.该ARUPF 方法具有噪声滤除效果好、精度高等优点.搭建CarSim 与Matlab/Simulink 联合仿真平台,对整车状态估计进行仿真分析验证.仿真结果表明,基于ARUPF 算法的整车状态估计具有精度高、抗干扰能力强、稳定性好的特点.
