木榫旋转焊接节点剪切试验研究与理论分析

贾贺然，高颖，孟鑫淼，杨鸿达，张也，徐飞扬

(1. 北京林业大学材料科学与技术学院，北京 100083; 2. 北京林业大学土木工程系，北京 100083)

木榫旋转焊接是一种新型无胶连接技术，高速旋转的木榫匀速进入基材预钻孔，木榫与基材接触面的温度因摩擦作用迅速升高，使得木榫中的木质素与半纤维素软化熔融，待试件冷却，熔融物质固化形成稳定的焊接界面层，从而实现连接[1]。木榫旋转焊接技术应用过程中无胶黏剂等化学试剂的使用，是一项环境友好型技术。同时，此技术具有美观、环保、可完全回收、生产效率高、操作简便等优点，满足当今社会对于绿色、低碳、环保、健康的要求，具有广阔的应用前景[2]。

现有研究多关注木榫焊接工艺参数、木榫预处理等因素对木榫焊接强度的影响，以及通过组分分析研究焊接机理。其中，研究的工艺参数主要包括木榫转速、孔径比、进给速度、树种、焊接时间以及焊接深度等。研究结果表明，树种、孔径比、进给速度对焊接强度的影响较为显著[3-5]，焊接时间和焊接深度需在一定范围内才能得到较高的焊接强度[6-7]。同时，利用CuCl2溶液、松香、乙烯乙二醇、乙酰化木质素、柠檬酸等对木榫进行预处理，可以增强焊接强度及节点耐水性能。其中使用CuCl2溶液浸渍木榫能够有效提高焊接试件的抗拉拔力[8]；使用植物油处理木榫，可以减小木榫进入木材的摩擦力，使木榫更容易进入木材中[9]；使用乙酰化木质素包覆在木榫表面，可以提高木榫焊接节点的强度及耐水性能[10]；使用柠檬酸作为防水剂能够提高耐水性及强度[11]。此外，利用傅里叶红外光谱(FT-IR)、扫描电子显微镜(SEM)、核磁共振碳谱(13CNMR)、热重分析(TG)、X射线光电子能谱(XPS)、气相色谱-质谱联用分析(Py-GCMS)等手段，对木榫旋转焊接机理及焊接界面层物质的变化及组成进行[6,12-18]研究。上述研究利用物理、化学等手段对木榫旋转焊接工艺和机理进行深入分析，但对其结构应用关注较少。

木榫旋转焊接强度主要通过木榫的抗拉拔强度和抗剪强度衡量。上述木榫旋转焊接工艺参数的研究中，主要利用抗拉拔性能来评估。而在工程应用中，木榫作为组合梁的抗剪连接件，其抗剪性能也是重要性能指标。El-houjeyri等[19]研究了压缩木榫的抗剪性能，并依据EN 26891和EN 12512标准要求在单调和循环载荷下分别开展剪切试验，结果表明压缩木榫比非压缩木榫抗剪性能提高1倍。Jung等[20]试验研究了日本雪松压缩木榫的双剪性能，结果表明压缩木材代替高密度硬木用作剪力连接件时，随着木榫密度的增加，峰值承载力增加，但延性系数下降。现有研究尚未涉及旋转焊接木榫的抗剪性能，其破坏机理的揭示和抗剪承载力计算方法的提出对于木榫旋转焊接工艺的工程应用具有重要意义。因此，为深入分析木组合梁中旋转焊接木榫的抗剪性能，本研究利用旋转焊接工艺，将单根山毛榉木榫旋转焊入3层SPF(spruce-pine-fir)层板，并开展双剪试验。基于试验结果和国内外相关规范，提出抗剪承载力计算公式，并利用ABAQUS开展有限元分析，为木榫旋转焊接技术的工程应用提供理论参考和设计依据。

1 材料与方法

1.1 试件设计与制备

试验中木榫采用直径12 mm、长为160 mm的斜纹山毛榉(Fagus)木材，密度为711 kg/m3，含水率调整为12%。基材采用38 mm×89 mm的SPF二级规格材，密度为450 kg/m3，含水率约为12%。

将SPF锯切为长度200 mm的基材用于制作中板和侧板，然后在基材预先钻出直径为10.7 mm的预钻孔，便于木榫旋转焊入。接着将木榫以转速1 430 r/min和进给速度10 mm/s，匀速焊入基材预钻孔内，试件示意图如图1所示。试件焊接完成静置1天，待其焊接层充分固化。同时，为与木榫旋转焊接试件进行对比，设计一组垂直敲入组试件。但由于预钻孔直径为10.7 mm时，试件制备过程中易发生基材劈裂，因此敲入组试件设计木榫直径为12 mm，预钻孔直径为11 mm，其余参数均与木榫旋转焊接组相同。

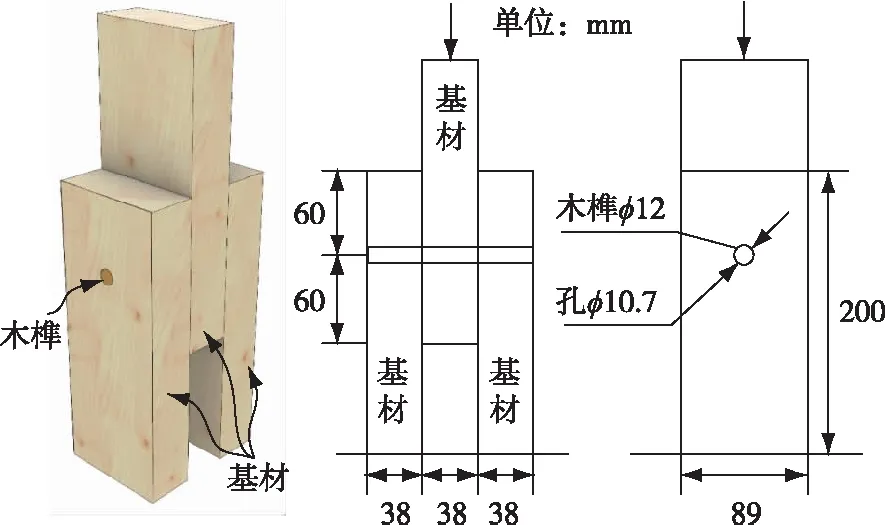
图1 试件示意图Fig. 1 Schematic view of the specimen

1.2 测试方法

1.2.1 材料性能测试

根据ASTM F1575-17《钉子屈服弯矩测定试验方法》规定对8个长度200 mm、直径12 mm的木榫进行抗弯试验。本研究连接件为木榫，但现有销槽承压性能测试标准均以金属销为试验对象，因此分别用钢销和木榫对SPF基材进行12，18个横纹销槽承压试验，对比钢销及木榫连接的SPF销槽承压强度。参照ASTM D5764-18《木材和木基制品榫支承强度评定试验方法》，采用半孔销槽承压形式，设置钢销孔洞直径比钢销大2 mm，而本试验中的木榫旋转焊接技术，使木榫与基材之间紧密连接，因此木榫孔洞直径与木榫直径相同。

1.2.2 抗剪性能测试

利用万能力学试验机(BMW-50)进行双剪试验，在加载头位置布置一个100 mm量程的位移计，测量其实际位移。为消除在加载初期因装配误差或木材中孔隙被压密对曲线造成的影响，在正式加载之前预压至0.8 kN后卸载至零。参照GB/T 14018—2009《木材握钉力试验方法》以2 mm/min的速度加载。当承载力下降至峰值承载力的80%，或木榫完全断裂时停止加载，观察试件破坏形态。

2 结果与分析

2.1 材料性能

试验得到山毛榉木榫的抗弯屈服承载力为0.517 kN，计算得到抗弯屈服弯矩为17 842.97 N·mm，屈服强度105.2 MPa，变异系数为16.8%。钢销连接SPF销槽承压强度为28.20 MPa，变异系数为7.03%；木榫连接SPF基材销槽承压强度为28.36 MPa，变异系数为15.1%。

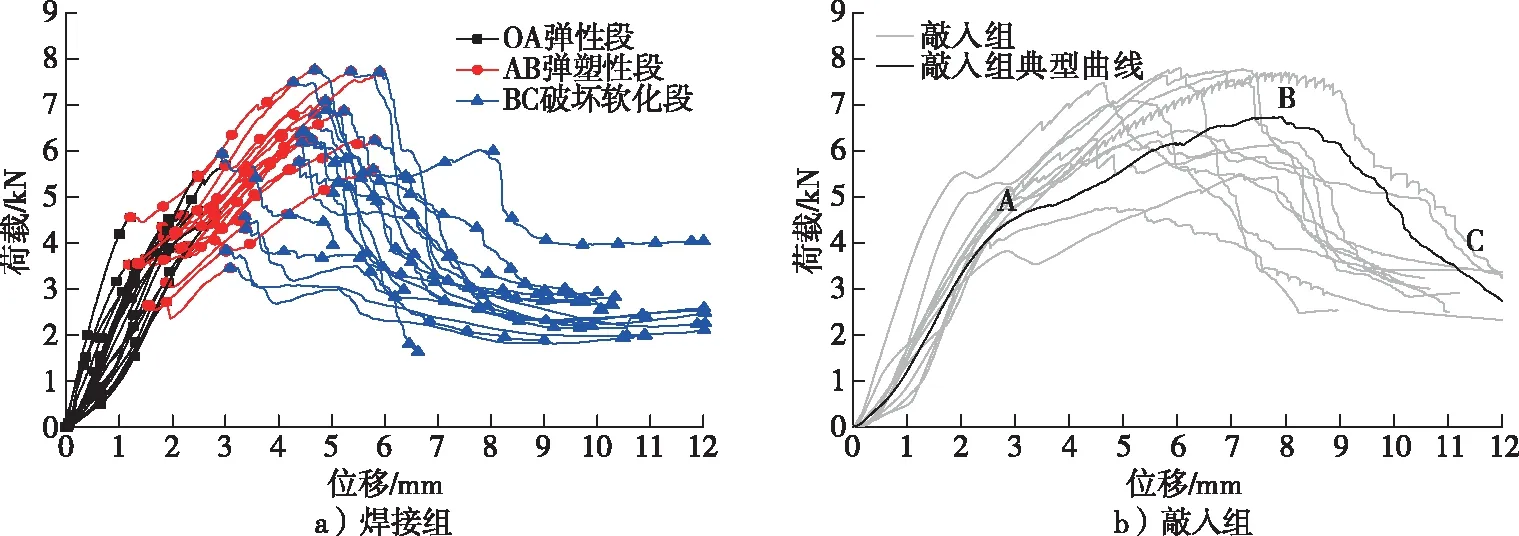
图3 试件荷载-位移曲线Fig. 3 Load-displacement curves of specimens in double-shear tests

2.2 旋转焊接

在焊接过程中，由于木榫高速旋转摩擦基材产生热量致使木材中木质素及半纤维素软化熔融，木榫与基材连接处产生了白烟和刺鼻气味，同时焊接界面层因高温而产生黑色炭化物质。由于焊接过程中白烟对基材的蒸熏，焊接结束后基材表面孔洞附近变黄。观察焊接后试件中的木榫，可发现下端木榫由于焊接时间较长，黑色焊接层物质损失；而上端木榫由于焊接时间较短，仅产生少量焊接物质；木榫中部焊接层物质较多，且粘连少量的SPF基材，表明此焊接层具有一定的粘接能力。

2.3 剪切试验现象

将处于加载过程中的试件沿中线锯开，观察测试过程中的木榫及基材的破坏现象，可以看到木榫的破坏模式为类双铰破坏，铰接处发生木材劈裂，如图2所示。同时，在荷载下降时可以听到明显的木材劈裂声。

图2 旋转焊接木榫破坏模式Fig. 2 Failure mode of rotation welding wood dowel

2.4 荷载-位移曲线

两组试件荷载-位移曲线如图3所示。主要包括3个阶段：①OA弹性阶段。此阶段木榫及基材无明显破坏，随着荷载的逐渐增加，木榫受到线弹性剪切作用，没有劈裂声音出现。②AB弹塑性阶段。在该阶段开始出现木材劈裂声，表明试件进入破坏阶段。曲线突降主要是由于木榫受剪力作用产生横纹挤压破坏；随着荷载的继续增加，木榫的破坏加剧，同时伴随着持续的劈裂声；但试件仍然具有一定的承载能力，荷载-位移曲线上升至峰值点(B点)，此刻木榫在层板连接处发生劈裂，劈裂声加大。且由于加载装置原因，导致木榫抗剪面存在法向应力，断裂面之间存在摩擦作用，导致出现曲线在A点小幅下降后再上升至峰值点。③BC破坏软化阶段。荷载到达峰值点之后木榫破坏加剧，但并未完全断裂，荷载-位移曲线下降，直至试件完全失效。

试件典型荷载-位移曲线如图4所示。图中：A点为第1次木榫发生挤压的位置，此时曲线发生小幅波动，木榫刚刚开始发生破坏，将此时的荷载定义为屈服荷载，对应位移为屈服位移；B点为曲线的峰值荷载，此时木榫已经发生较为严重的破坏，B点之前有较小连续的木材劈裂声，在B点之后有持续的较大劈裂声，承载力逐渐下降。

为了分析在试验过程中木榫和基材的损伤过程和破坏机理，分别在试件加载至A点和B点位置时停止加载，将试件沿中间轴切开，观察剖面的木榫及基材的破坏状态。图4包含A、B两点位置时木榫的剖面图。可以看出，在A点位置基材无明显破坏，但此时木榫由于受到剪力作用，层板连接位置的木榫受到挤压，承载力降低，荷载-位移曲线出现小幅下降。木榫在峰值承载力时典型的试件破坏形态如图中B点所示，从图中可以观察出木榫在基材接触面位置受到挤压作用发生断裂破坏，导致承载力开始逐渐下降。

图4 试件破坏过程Fig. 4 Failure progress of specimens in double-shear tests

2.5 剪切承载力

将屈服点A、峰值点B的荷载及位移汇总如表1所示，其中初始刚度取荷载-位移曲线中10%～40%Pmax(峰值荷载)线性段斜率。

由表1可知，由于木材离散性较大以及可能的加工误差，初始刚度的变异性较大，但各参数变异系数均小于25%；同时可以看到屈服位移均处于1～3 mm之间，平均峰值位移4.460 mm，与试验现象基本符合。表明木榫在加载到屈服点位置时已产生横纹受压变形，到达峰值位移时木榫已发生剪切破坏。敲入组试件的平均峰值荷载为6.786 kN，较木榫旋转焊接组试件的峰值荷载稍大一点，主要是由于敲入组试件的预钻孔直径相对较大，试件制备过程中，木榫损伤小，其实际直径相对较大，因此其承载力较大。

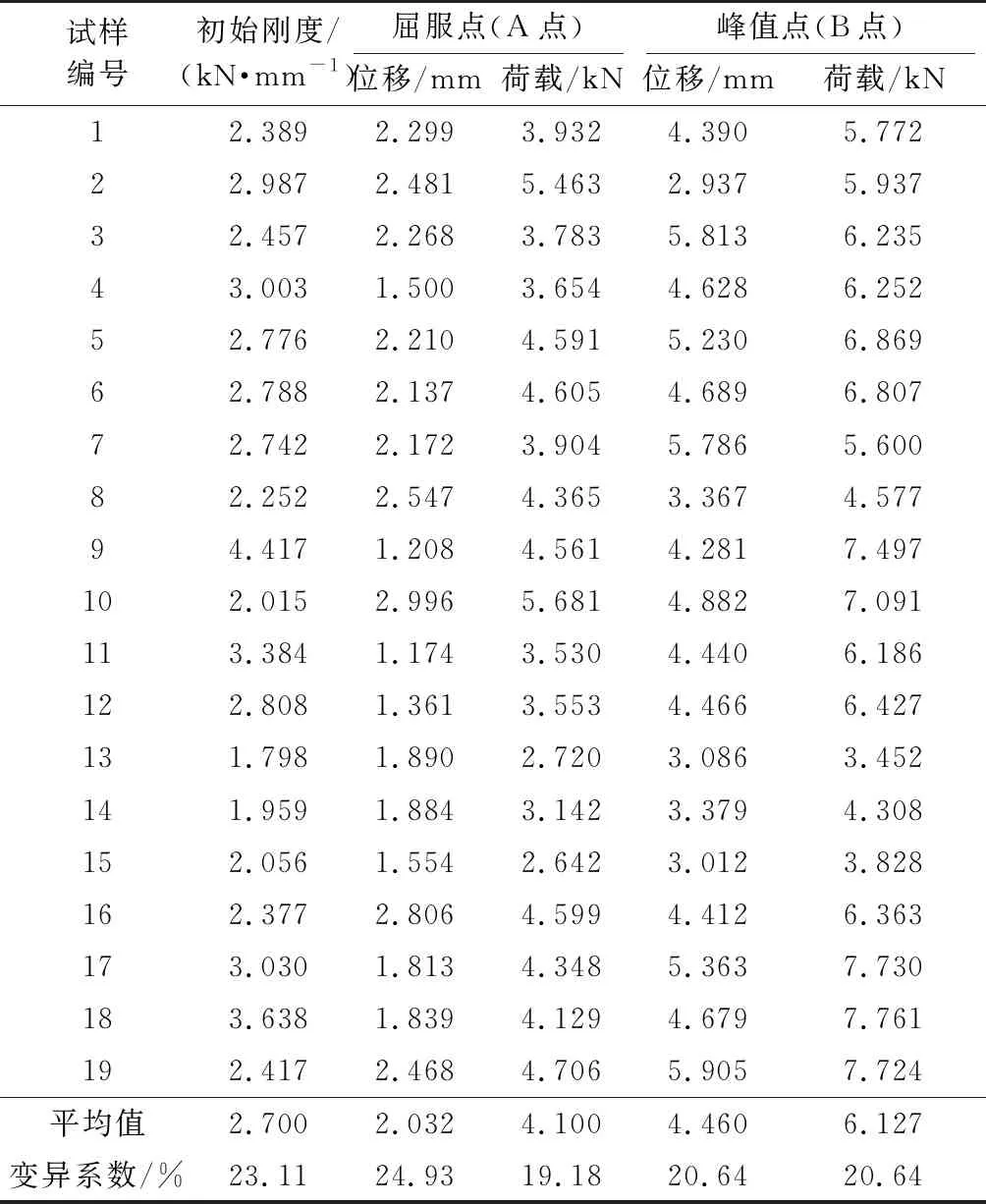
表1 旋转焊接单榫双剪试验结果Table 1 Test results of single-dowel rotation welding specimens

3 理论计算

本试验中木榫的破坏模式为类双铰破坏；SPF层板出现开孔处局部挤压破坏。采用现有标准及规范对木榫连接件的抗剪承载力进行计算。

3.1 我国木结构设计标准(GB 50005—2017)

本试验中木榫的破坏模式符合《木结构设计标准》中的屈服模式IV，则单个连接件的抗剪承载力计算公式为：

NGB 50005=2kIVtsdfes

(1)

式中：kIV为对应屈服模式下边部构件的销槽承压有效长度系数，按标准第6.2.7条规定，按照公式(2)计算；ts为边部构件的厚度，取值38 mm；d为连接件直径，取值12 mm；fes为销槽承压强度，根据本文2.1 节，取值28.36 MPa。

(2)

式中：Re为中部构件与边部构件得销槽承压强度之比，取值1；kep为弹塑性强化系数，取值1；fyk为连接件屈服强度，根据本文2.1节，取值105.2 MPa。

3.2 美国木结构设计规范(NDSWC-2018)

NDSWC-2018中，与本试验中木榫的破坏模式对应双剪对称连接抗剪承载力计算公式为：

(3)

式中：N为节点承载力，单位为N；d为连接件直径，取12 mm；fyk为连接件屈服强度，根据本文2.1节，取105.2 MPa；fes为销槽承压强度，根据本文2.1节，取28.36 MPa；Re为中部构件与边部构件得销槽承压强度之比，取1。

3.3 欧洲木结构设计规范(Eurocode 5-1995)

对应屈服模式下，EC5中规定双剪连接承载力按下式计算：

(4)

式中：N为节点承载力，N；b为中部构件与边部构件得销槽承压强度之比，取1；My为连接件抗弯屈服弯矩，根据本文2.1节，取17 842.97 N·mm；fes为边部构件销槽承压强度，根据本文2.1节，取28.36 MPa；d为连接件直径，12 mm；fax为连接件的轴向力，取0。

根据上述规范计算旋转焊接木榫连接节点抗剪承载力，得到计算结果如表2所示。可以看出，现有国内外标准中公式得到的计算值与试验值误差较大。这主要是因为现有标准的公式均针对钢销连接计算，钢材与木材的弹塑性行为差别较大，计算得到结果仅为理论结果，未考虑到加载过程中的界面摩擦，以及在焊接过程中木榫存在一定程度的损伤，导致计算值均大于试验值；且试验过程中无绳索效应产生，其计算误差较大。

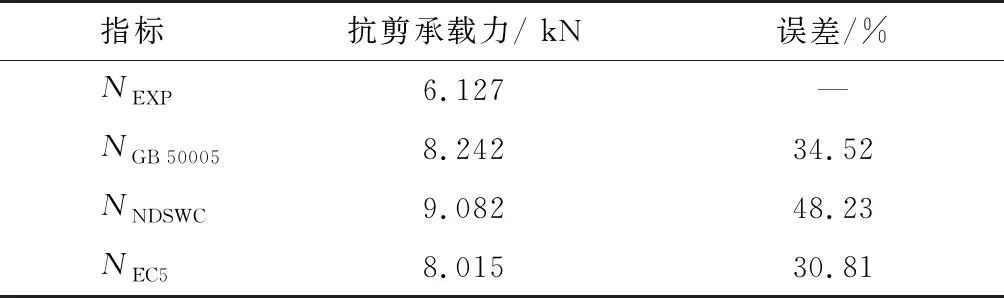
表2 规范计算值与试验值对比Table 2 Comparisons of calculated and test results

4 受力分析

根据本试验中木榫的实际受力情况及破坏模式进行分析，如图5所示，对层板连接处木榫进行受力分析。

图5 双剪试验中旋转焊接木榫受力分析模型Fig. 5 Analytical model of the rotation welding dowel in double-shear tests

根据木榫的受力及弯矩平衡分析，得到以下两个公式：

(5)

(6)

式中：F为整个试件所受的承载力，N；fes，fem分别为侧板与中板的销槽承压强度，MPa；ls，lm为侧板与中板中塑性铰到受剪面之间的距离，mm；d为连接件直径，12 mm；My为木榫抗弯屈服弯矩，N·mm。

由于本试验中部板材与边部板材为同种材料，因此有：

fes=fem

(7)

将公式(7)代入公式(5)中得到：

ls=lm

(8)

将公式(7)、(8)代入(6)式中，得到：

(9)

将公式(9)代入(5)式中，得到：

(10)

式中：F/2为单个剪面节点承载力，N；My为连接件抗弯屈服弯矩，根据本文2.1节，取17 842.97 N·mm；fem为边部构件销槽承压强度，根据本文2.1节，取28.36 MPa。

以木榫直径为12 mm，利用公式(9)计算得到，木榫抗剪承载力为6.970 kN，与焊接组试验值误差为13.76%，与敲入组试件误差仅为2.71%。本研究提出的公式与上文中参照各标准计算结果相比，此公式较现有标准有更好的准确性，因此适用于木榫连接试件。相比于敲入组试件，焊接组试件误差较大，主要是由于焊接过程中，木榫的损伤导致木榫实际直径小于名义直径12 mm。

5 有限元分析

利用有限元软件ABAQUS进行模拟，进一步对试件的抗剪性能及受力机理进行探究。SPF及山毛榉木的各向材料属性根据GB 50005—2017《木结构设计标准》及美国“Wood Handbook”[21]得出，如表3所示。基材与木榫均采用三维缩减积分单元(C3D8R)，经收敛性分析，基材厚度方向网格尺寸为9 mm，3块基材各3 120个单元，木榫共3 840 个单元，试件网格如图6所示。采用Cohesive Behavior分析模拟木榫表面与基材预钻孔表面之间焊接层，其中切向刚度根据拉拔试验取2 MPa。加载过程采用位移控制加载。为便于施加约束和位移，在中板上端设置参考点并与上端面建立耦合作用(coupling)，在两个侧板底面及侧面施加固定约束，防止侧板向两边旋转侧翻，采用位移控制方式进行加载。层板之间采用摩擦接触，摩擦系数为0.1。

表3 木材材性参数Table 3 Material properties for numerical simulation

图6 有限元数值模拟网格划分Fig. 6 Mesh of finite element numerical simulation

图7a和b为试件加载破坏应力云图，可以看到木榫破坏现象与试验相吻合。图7a显示，木榫在层板连接处受剪力作用，发生破坏；基材预钻孔周围，特别是侧板预钻孔下方及中间层板的预钻孔上方，由于受到木榫的挤压作用造成破坏，与试验现象较为吻合。同时通过对比观察得到，有限元模型在荷载-位移曲线的A点位置时，木榫开始产生了塑性应变，而基材并未产生塑性应变，因此此点位置开始试件产生塑性变形。

图7c为试件荷载-位移曲线的试验与有限元模拟对比结果。结果显示，在加载初期初始刚度段较吻合，局部破坏阶段也基本上处于几组曲线的平均值左右，然后试件失效荷载下降。且有限元模拟峰值荷载为6.934 kN，比试验值偏大13.17%。

图7 有限元分析结果Fig. 7 Results of the finite element analysis

6 结 论

本研究选用山毛榉木榫旋转焊接SPF层板开展了双剪试验，获得其破坏模式及荷载-位移曲线。通过分析比较试验结果与中、美、欧木结构标准及规范的理论计算结果，提出木榫旋转焊接节点计算公式，并建立了考虑焊接界面的有限元模型。具体结论如下：

1)旋转焊接单榫节点双剪试验中木榫受剪呈现类双铰破坏模式并最终断裂，两侧基材在预钻孔下方出现挤压破坏，试验后旋转焊接界面良好，未观测到木榫在预钻孔中的滑脱。

2)木榫旋转焊接单榫双剪试件屈服荷载均值为4.100 kN，峰值荷载均值为6.127 kN，峰值位移均值为4.460 mm，各参数的变异系数均小于25%。

3)采用中国GB 50005—2017《木结构设计标准》、美国NDSWC-2018木结构设计规范、欧洲Eurocode 5-1995木结构设计规范中金属销连接件抗剪承载力计算公式，误差均大于28%。基于试验现象，不考虑绳索效应，本研究提出的抗剪承载力计算公式与试验误差为13.76%，具有较高的准确性。

4)采用ABAQUS软件建立有限元模型，利用Cohesive Behavior模拟焊接界面，结果表明，本研究提出的有限元分析方法能较准确预测旋转焊接木榫双剪试件的破坏模式，荷载-位移曲线与试验曲线较为吻合。