高压涡轮导叶传热数值计算与分析

2022-02-25王建华葛宁

机械制造与自动化 2022年1期

王建华，葛宁

(南京航空航天大学能源与动力学院，江苏南京 210016)

0 引言

在现代燃气涡轮发动机中，高压涡轮导叶与燃气热交换率最高。因涡轮进口温度远超过金属叶片的熔点温度，故必需大量使用冷却气体，这就要求在设计过程中准确地预测涡轮叶片表面温度分布。丁林[1]搭建了涡轮叶片测温平台，利用光学扫描和辐射测温方法对叶片表面温度分布进行测量。近年来，研究人员对气热耦合方法进行了广泛研究。LUO J等[2]研究了涡轮导叶在3种典型工况下的气动和传热特性，采用不同的湍流模型计算分析了叶中截面处温度分布和外换热系数分布。褚云会等[3]对跨音速涡轮数值模拟，分析了网格量和湍流模型对计算结果的影响。CROCE G[4]将开发的程序和商业软件进行了耦合，即流体域和固体域使用不同的网格，通过插值程序将流固交接面上的信息进行传递。郭兆元等[5]采用耦合和非耦合方式对单级涡轮机叶片数值计算，表明两种计算方法对流场结构影响不大，只有耦合计算能准确地预测温度分布。虽然耦合计算正确地设置了流固交接面上边界条件，但是，在计算复杂的内部冷却结构时，这种方法在工程应用上受到限制。因此，在研究冷却问题时，有学者提出用外换热系数定量描述对流换热现象，这也是工程上初步设计冷却系统的常用方法。

本文首先在典型工况下对C3X计算域进行数值敏感性验证。然后采用非耦合方法计算分析了壁面温度对外换热系数(HTC)的影响。采用耦合方法对比了不同湍流模型下HTC分布。最后对改进的换热量预测方法进行可行性分析并对比不同计算方法下的HTC。

1 求解方法及验证

采用课题组自主研发的NUAA-TURBO三维数值求解器和ANSYS-CFX求解器求解雷诺平均Navier-Stokes方程(RANS)。通过Numeca对C3X叶型建立计算域网格，如图1所示，其中进、出口为H型网格，叶片表面建立O型网格。由于热边界层受网格影响较大，为了正确模拟传热，叶片表面的y+值<1，网格节点数达2×107。计算域边界条件如下：来流总压P0=3.218×105Pa，来流总温T0in=783K，出口马赫数Maisout=0.89，湍动量Tu=8.3%，湍流长度尺度为0.005m。

图1 计算域网格及边界条件

1.1 网格无关性验证

首先改变沿叶片轮廓周围边界层中的O型网格节点，使用NUAA-TURBO求解器来进行网格无关性验证。在保证离壁距离相同的情况下，比较了3种不同的网格节点。如图2所示，在温度比TR=Tw/T0in=0.65时，计算了30、40和50个节点下叶片表面的无量纲换热量q/qref分布。无量纲换热量的计算方法见式(1)，换热量q通过壁面附近流体分子之间导热计算，即q=-k(∂T/∂n)。C为叶片轴向弦长，k为进口温度条件下的导热系数。从整体上看，3种网格节点下的计算结果差异很小，在之后的计算中选择网格节点为40。

(1)

图2 TR=0.65时不同边界层节点HTC分布

1.2 非耦合计算

通过NUAA-TURBO求解器的定量计算来分析TR对HTC的影响。计算域的边界条件如上所述，在不同工况下，仅仅改变壁面温度边界条件。假设空气为理想气体，理想气体定律和萨瑟兰黏性定律来求解气体的状态和热物理性质。从图3中可以清楚地看出叶片壁面温度对HTC的影响。在叶片尾缘的相同位置处，在TR=0.60情况下的HTC比TR=0.95情况下高30%左右。同时，在叶片前缘的驻点区域，TR对HTC的影响不如尾缘区域明显。这也表明上游历史效应对边界层的影响。在叶片前缘附近，由于边界层刚形成，对壁面的温度影响较小，但是，随着边界层在叶片表面的发展，相比于边界层外部流动，温度不同的流体在边界层内部逐渐积累并且不断影响壁面温度。这表明当地壁面温度条件影响HTC，同时受冷却表面的外换热系数还与上游边界层发展历程相关。

图3 外换热系数HTC依赖于TR

1.3 耦合计算

在非耦合计算中只是考虑外部气动影响。正如在数值计算时，都是给定等温边界条件，这就改变了叶片表面和流体域之间的真实交界面边界条件。为了排除这种任意边界条件的影响，采用CFX求解器中的热-固耦合模型数值计算。图4给出了耦合计算域，外部流体域与非耦合计算下的边界条件一致，叶片内部固体域材料选择热导率较低的ASTM310型不锈钢，在叶片内部有10个冷却通道，每个冷却通道进口给定半径、进口质量流量、进口静温和湍流度。这里选择文献[6]中4422工况。

图4 耦合计算域

图5显示了不同湍流模型下，叶片表面无量纲静压分布，计算结果表明湍流模型对气动特性的影响较小。在压力面，从叶片前缘到x/Cax=-0.5附近，压力几乎保持不变，这个阶段流体加速缓慢，叶片表面没有分离，边界层内的静压梯度为0，叶片表面的压力分布受湍流模型的影响很小。从压力面中部到尾缘附近，压差增大，流体急剧加速。在吸力面，从前缘到x/Cax=0.4附近，静压快速下降到进口压力的一半。随后流体开始减速，到尾缘附近，流体又经历了缓慢地加速的过程。

图5 不同湍流模型下叶片表面静压分布

如图6所示，不同湍流模型下换热系数与实验值对比。从整体上看，边界层内部的转捩流动对HTC有较大影响。在吸力面前缘沿叶片表面下游，不同湍流模型对外换热系数的预测都有不同程度的偏差。高雷诺数湍流模型(k-ε类)主要模拟湍流状态，使用半经验公式简化边界层流动，计算所得的湍流强度比较高，同时在吸力面前缘附近，激波-附面层相互干扰的现象极为明显，对计算结果有较大影响。尽管低雷诺数湍流模型(k-ω类)计算所得的湍流强度较低，但是仍然反映边界层内部的湍动特性。对于吸力面前缘附近的层流区域，无法准确地分辨。如果在k-ωSST湍流模型上使用转捩模型，预测的HTC与实验值吻合较好。

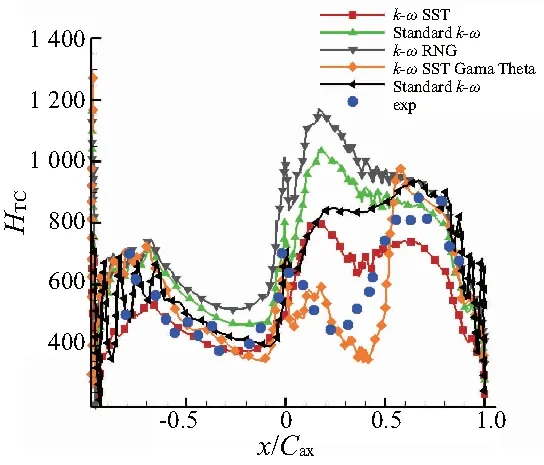
图6 不同湍流模型下HTC对比

2 非线性方法可行性分析

在典型非耦合计算中假设：气动性能决定换热性能。对于给定的叶型结构和流动条件，在牛顿冷却定律q=h(T-Taw)中，有两个由气动决定的未知量(h，Taw)。由于这两个未知量不受壁温影响，h值能正确地表示为每一点处的曲线斜率，可将其改写成式(2)的形式。

(2)

当q与Tw呈现明显的非线性关系时，曲线斜率表现为在当地变化。式(2)改写成式(3)。此时式(3)中的外换热系数h可以解释为微分算子dq/dTw的有限差分近似，对于给定的壁温Tw，在极小的温差ΔT范围内，曲线的局部斜率能正确地表示外换热系数。

(3)

为了确定式(3)中ΔT的取值大小，在TR=0.70条件下，选取3K、5K和10K进行验证研究。为了在图中显示清晰，去掉了尾缘回流区域内和转捩附近HTC分布的峰值点。如图7所示，在所选取的3个温差下，计算所得外换热系数基本相同，因此，在下面两点法的计算中选择5K。

图7 3种温差下叶中截面外换热系数分布

根据非耦合计算结果中的分析，非线性方法主要考虑了HTC与Tw呈现线性关系，即HTC=h0+h1Tw。不考虑绝热壁温随壁面温度的变化。具体表达式如下：

q=(h0+h1Tw)(Tw-Taw)

(4)

在3个壁温下，求解式(4)中的未知变量h0,h1和Taw。这些未知变量确定后，就可以根据式(4)确定未知Tw下的换热量分布以及对应壁面温度下的HTC。未知变量也是叶片表面上的每个网格点的常数。这种当地校正方法与相关经验关系式有明显地区别。求解叶片表面HTC分布的常规做法是需要不同壁温下两个CFD计算解。该方法只需要3个CFD解，计算成本低，而预测精度得到质的提高。

在温度比为0.95、0.75和0.65条件下，使用NUAA-TURBO求解器得到每个网格点的换热量来求解式(4)。用非线性方法可以预测温度比为0.6～0.95范围内的换热量。图8比较了非线性方法的计算结果与数值计算结果。这种方法可确保在整个Tw范围内，预测结果与CFD数值计算结果的匹配非常好。为了突出HTC独立于Tw的假设所带来的误差，还使用传统的两点法预测了温度比分别为0.7、0.8和0.9下的换热量。如图9所示，结果表明两点法无法体现HTC随壁面温度的变化，从而在换热量的预测中带来误差。

图8 CFD解与非线性方法的换热量对比

图9 CFD解与两点法的换热量对比

3 外换热系数分布

图10对比了叶片表面平均温度TR=0.84情况下，两点法、非线性方法以及耦合计算下的HTC分布。在校正过程中，两点法在转捩附近出现了尖峰值，与两点法相比，非线性方法预测的外换热系数值更加稳定，这种稳定性主要是对不同壁面稳定范围内的多点曲线拟合，而传统的两点法只是基于单个壁面温度上局部区域内的差分近似。如图10所示，非线性方法在转捩位置处与实验值和耦合计算有些误差，从整体上看，可以较为准确地预测外换热系数。